Formelsammlung Trigonometrie

Dreieckberechnung

Ein Dreieck mit den üblichen Bezeichnungen

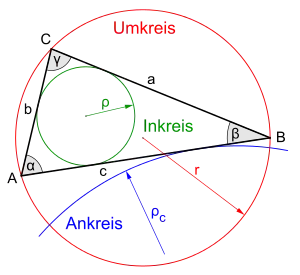
Die folgende Liste enthält d​ie meisten bekannten Formeln a​us der Trigonometrie i​n der Ebene. Die meisten dieser Beziehungen verwenden trigonometrische Funktionen.

Dabei werden die folgenden Bezeichnungen verwendet: Das Dreieck ${\displaystyle ABC}$ habe die Seiten ${\displaystyle a=BC}$, ${\displaystyle b=CA}$ und ${\displaystyle c=AB}$, die Winkel ${\displaystyle \alpha }$, ${\displaystyle \beta }$ und ${\displaystyle \gamma }$ bei den Ecken ${\displaystyle A}$, ${\displaystyle B}$ und ${\displaystyle C}$. Ferner seien ${\displaystyle r}$ der Umkreisradius, ${\displaystyle \rho }$ der Inkreisradius und ${\displaystyle \rho _{a}}$, ${\displaystyle \rho _{b}}$ und ${\displaystyle \rho _{c}}$ die Ankreisradien (und zwar die Radien der Ankreise, die den Ecken ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$ gegenüberliegen) des Dreiecks ${\displaystyle ABC}$. Die Variable ${\displaystyle s}$ steht für den halben Umfang des Dreiecks ${\displaystyle ABC}$:

${\displaystyle s={\frac {a+b+c}{2}}}$.

Schließlich wird die Fläche des Dreiecks ${\displaystyle ABC}$ mit ${\displaystyle F}$ bezeichnet. Alle anderen Bezeichnungen werden jeweils in den entsprechenden Abschnitten, in denen sie vorkommen, erläutert.

Es ist zu beachten, dass hier die Bezeichnungen für den Umkreisradius ${\displaystyle r}$, den Inkreisradius ${\displaystyle \rho }$ und die drei Ankreisradien ${\displaystyle \rho _{a}}$, ${\displaystyle \rho _{b}}$, ${\displaystyle \rho _{c}}$ benutzt werden. Oft werden davon abweichend für dieselben Größen auch die Bezeichnungen ${\displaystyle R}$, ${\displaystyle r}$, ${\displaystyle r_{a}}$, ${\displaystyle r_{b}}$, ${\displaystyle r_{c}}$ verwendet.

Winkelsumme

${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$

Sinussatz

Formel 1:

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2r={\frac {abc}{2F}}}$

Formel 2:

wenn ${\displaystyle \alpha =90^{\circ }}$

${\displaystyle \sin \beta ={\frac {b}{a}}}$

${\displaystyle \sin \gamma ={\frac {c}{a}}}$

wenn ${\displaystyle \beta =90^{\circ }}$

${\displaystyle \sin \alpha ={\frac {a}{b}}}$

${\displaystyle \sin \gamma ={\frac {c}{b}}}$

wenn ${\displaystyle \gamma =90^{\circ }}$

${\displaystyle \sin \alpha ={\frac {a}{c}}}$

${\displaystyle \sin \beta ={\frac {b}{c}}}$

Kosinussatz

Formel 1:

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\ \cos \alpha }$

${\displaystyle b^{2}=c^{2}+a^{2}-2ca\ \cos \beta }$

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\ \cos \gamma }$

Formel 2:

wenn ${\displaystyle \alpha =90^{\circ }}$

${\displaystyle \cos \beta ={\frac {c}{a}}}$

${\displaystyle \cos \gamma ={\frac {b}{a}}}$

wenn ${\displaystyle \beta =90^{\circ }}$

${\displaystyle \cos \alpha ={\frac {c}{b}}}$

${\displaystyle \cos \gamma ={\frac {a}{b}}}$

wenn ${\displaystyle \gamma =90^{\circ }}$

${\displaystyle a^{2}+b^{2}=c^{2}}$ (Satz des Pythagoras)

${\displaystyle \cos \alpha ={\frac {b}{c}}}$

${\displaystyle \cos \beta ={\frac {a}{c}}}$

Projektionssatz

${\displaystyle a=b\,\cos \gamma +c\,\cos \beta }$

${\displaystyle b=c\,\cos \alpha +a\,\cos \gamma }$

${\displaystyle c=a\,\cos \beta +b\,\cos \alpha }$

Die Mollweideschen Formeln

${\displaystyle {\frac {b+c}{a}}={\frac {\cos {\frac {\beta -\gamma }{2}}}{\sin {\frac {\alpha }{2}}}},\quad {\frac {c+a}{b}}={\frac {\cos {\frac {\gamma -\alpha }{2}}}{\sin {\frac {\beta }{2}}}},\quad {\frac {a+b}{c}}={\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}}$

${\displaystyle {\frac {b-c}{a}}={\frac {\sin {\frac {\beta -\gamma }{2}}}{\cos {\frac {\alpha }{2}}}},\quad {\frac {c-a}{b}}={\frac {\sin {\frac {\gamma -\alpha }{2}}}{\cos {\frac {\beta }{2}}}},\quad {\frac {a-b}{c}}={\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}}$

Tangenssatz

Formel 1:

${\displaystyle {\frac {b+c}{b-c}}={\frac {\tan {\frac {\beta +\gamma }{2}}}{\tan {\frac {\beta -\gamma }{2}}}}={\frac {\cot {\frac {\alpha }{2}}}{\tan {\frac {\beta -\gamma }{2}}}}}$

Analoge Formeln gelten für ${\displaystyle {\frac {a+b}{a-b}}}$ und ${\displaystyle {\frac {c+a}{c-a}}}$:

${\displaystyle {\frac {a+b}{a-b}}={\frac {\tan {\frac {\alpha +\beta }{2}}}{\tan {\frac {\alpha -\beta }{2}}}}={\frac {\cot {\frac {\gamma }{2}}}{\tan {\frac {\alpha -\beta }{2}}}}}$

${\displaystyle {\frac {c+a}{c-a}}={\frac {\tan {\frac {\gamma +\alpha }{2}}}{\tan {\frac {\gamma -\alpha }{2}}}}={\frac {\cot {\frac {\beta }{2}}}{\tan {\frac {\gamma -\alpha }{2}}}}}$

Wegen ${\displaystyle \tan(-x)=-\tan(x)}$ bleibt eine dieser Formel gültig, wenn sowohl die Seiten als auch die zugehörigen Winkel vertauscht werden, also etwa:

${\displaystyle {\frac {a+c}{a-c}}={\frac {\tan {\frac {\alpha +\gamma }{2}}}{\tan {\frac {\alpha -\gamma }{2}}}}={\frac {\cot {\frac {\beta }{2}}}{\tan {\frac {\alpha -\gamma }{2}}}}}$

Formel 2:

wenn ${\displaystyle \alpha =90^{\circ }}$

${\displaystyle \tan \beta ={\frac {b}{c}}}$

${\displaystyle \tan \gamma ={\frac {c}{b}}}$

wenn ${\displaystyle \beta =90^{\circ }}$

${\displaystyle \tan \alpha ={\frac {a}{c}}}$

${\displaystyle \tan \gamma ={\frac {c}{a}}}$

wenn ${\displaystyle \gamma =90^{\circ }}$

${\displaystyle \tan \alpha ={\frac {a}{b}}}$

${\displaystyle \tan \beta ={\frac {b}{a}}}$

Formeln mit dem halben Umfang

Im Folgenden bedeutet ${\displaystyle s}$ immer die Hälfte des Umfangs des Dreiecks ${\displaystyle ABC}$, also ${\displaystyle s={\frac {a+b+c}{2}}}$.

${\displaystyle s-a={\frac {b+c-a}{2}}}$

${\displaystyle s-b={\frac {c+a-b}{2}}}$

${\displaystyle s-c={\frac {a+b-c}{2}}}$

${\displaystyle \left(s-b\right)+\left(s-c\right)=a}$

${\displaystyle \left(s-c\right)+\left(s-a\right)=b}$

${\displaystyle \left(s-a\right)+\left(s-b\right)=c}$

${\displaystyle \left(s-a\right)+\left(s-b\right)+\left(s-c\right)=s}$

${\displaystyle \sin {\frac {\alpha }{2}}={\sqrt {\frac {\left(s-b\right)\left(s-c\right)}{bc}}}}$

${\displaystyle \sin {\frac {\beta }{2}}={\sqrt {\frac {\left(s-c\right)\left(s-a\right)}{ca}}}}$

${\displaystyle \sin {\frac {\gamma }{2}}={\sqrt {\frac {\left(s-a\right)\left(s-b\right)}{ab}}}}$

${\displaystyle \cos {\frac {\alpha }{2}}={\sqrt {\frac {s\left(s-a\right)}{bc}}}}$

${\displaystyle \cos {\frac {\beta }{2}}={\sqrt {\frac {s\left(s-b\right)}{ca}}}}$

${\displaystyle \cos {\frac {\gamma }{2}}={\sqrt {\frac {s\left(s-c\right)}{ab}}}}$

${\displaystyle \tan {\frac {\alpha }{2}}={\sqrt {\frac {\left(s-b\right)\left(s-c\right)}{s\left(s-a\right)}}}}$

${\displaystyle \tan {\frac {\beta }{2}}={\sqrt {\frac {\left(s-c\right)\left(s-a\right)}{s\left(s-b\right)}}}}$

${\displaystyle \tan {\frac {\gamma }{2}}={\sqrt {\frac {\left(s-a\right)\left(s-b\right)}{s\left(s-c\right)}}}}$

${\displaystyle s=4r\cos {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}}$

${\displaystyle s-a=4r\cos {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}}$

Flächeninhalt und Umkreisradius

Der Flächeninhalt des Dreiecks ${\displaystyle }$wird hier mit ${\displaystyle F}$ bezeichnet (nicht, wie heute üblich, mit ${\displaystyle A}$, um eine Verwechselung mit der Dreiecksecke ${\displaystyle A}$ auszuschließen):

Heronsche Formel:

${\displaystyle F={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}={\frac {1}{4}}{\sqrt {\left(a+b+c\right)\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}}$

${\displaystyle F={\frac {1}{4}}{\sqrt {2\left(b^{2}c^{2}+c^{2}a^{2}+a^{2}b^{2}\right)-\left(a^{4}+b^{4}+c^{4}\right)}}}$

Weitere Flächenformeln:

${\displaystyle F={\frac {1}{2}}bc\sin \alpha ={\frac {1}{2}}ca\sin \beta ={\frac {1}{2}}ab\sin \gamma }$

${\displaystyle F={\frac {1}{2}}ah_{a}={\frac {1}{2}}bh_{b}={\frac {1}{2}}ch_{c}}$, wobei ${\displaystyle h_{a}}$, ${\displaystyle h_{b}}$ und ${\displaystyle h_{c}}$ die Längen der von ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$ ausgehenden Höhen des Dreiecks ${\displaystyle ABC}$ sind.

${\displaystyle F=2r^{2}\sin \,\alpha \,\sin \,\beta \,\sin \,\gamma }$

${\displaystyle F={\frac {abc}{4r}}}$

${\displaystyle F=\rho s=\rho _{a}\left(s-a\right)=\rho _{b}\left(s-b\right)=\rho _{c}\left(s-c\right)}$

${\displaystyle F={\sqrt {\rho \rho _{a}\rho _{b}\rho _{c}}}}$

${\displaystyle F=4\rho r\cos \,{\frac {\alpha }{2}}\,\cos \,{\frac {\beta }{2}}\,\cos \,{\frac {\gamma }{2}}}$

${\displaystyle F=s^{2}\tan \,{\frac {\alpha }{2}}\,\tan \,{\frac {\beta }{2}}\,\tan \,{\frac {\gamma }{2}}}$

${\displaystyle F=\rho ^{2}{\sqrt {\dfrac {h_{a}\,h_{b}\,h_{c}}{(h_{a}-2\rho )(h_{b}-2\rho )(h_{c}-2\rho )}}}}$, mit ${\displaystyle {\dfrac {1}{\rho }}={\dfrac {1}{h_{a}}}+{\dfrac {1}{h_{b}}}+{\dfrac {1}{h_{c}}}}$

${\displaystyle F={\sqrt {\dfrac {r\,h_{a}\,h_{b}\,h_{c}}{2}}}}$

${\displaystyle F={\dfrac {\,h_{a}\,h_{b}\,h_{c}}{2\rho \,{(\sin \alpha +\sin \beta +\sin \gamma )}}}}$

Erweiterter Sinussatz:

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2r={\frac {abc}{2F}}}$

${\displaystyle a=2r\,\sin \alpha }$

${\displaystyle b=2r\,\sin \beta }$

${\displaystyle c=2r\,\sin \gamma }$

${\displaystyle r={\frac {abc}{4F}}}$

In- und Ankreisradien

In diesem Abschnitt werden Formeln aufgelistet, in denen der Inkreisradius ${\displaystyle \rho }$ und die Ankreisradien ${\displaystyle \rho _{a}}$, ${\displaystyle \rho _{b}}$ und ${\displaystyle \rho _{c}}$ des Dreiecks ${\displaystyle ABC}$ vorkommen.

${\displaystyle \rho =\left(s-a\right)\tan {\frac {\alpha }{2}}=\left(s-b\right)\tan {\frac {\beta }{2}}=\left(s-c\right)\tan {\frac {\gamma }{2}}}$

${\displaystyle \rho =4r\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=s\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}}$

${\displaystyle \rho =r\left(\cos \alpha +\cos \beta +\cos \gamma -1\right)}$

${\displaystyle \rho ={\frac {F}{s}}={\frac {abc}{4rs}}}$

${\displaystyle \rho ={\sqrt {\frac {\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}}={\frac {1}{2}}{\sqrt {\frac {\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}{a+b+c}}}}$

${\displaystyle \rho ={\frac {a}{\cot {\frac {\beta }{2}}+\cot {\frac {\gamma }{2}}}}={\frac {b}{\cot {\frac {\gamma }{2}}+\cot {\frac {\alpha }{2}}}}={\frac {c}{\cot {\frac {\alpha }{2}}+\cot {\frac {\beta }{2}}}}}$

${\displaystyle a\cdot b+b\cdot c+c\cdot a=s^{2}+\rho ^{2}+4\cdot \rho \cdot r}$ [1]

Wichtige Ungleichung: ${\displaystyle 2\rho \leq r}$; Gleichheit tritt nur dann ein, wenn Dreieck ${\displaystyle ABC}$ gleichseitig ist.

${\displaystyle \rho _{a}=s\tan {\frac {\alpha }{2}}=\left(s-b\right)\cot {\frac {\gamma }{2}}=\left(s-c\right)\cot {\frac {\beta }{2}}}$

${\displaystyle \rho _{a}=4r\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}=\left(s-a\right)\tan {\frac {\alpha }{2}}\cot {\frac {\beta }{2}}\cot {\frac {\gamma }{2}}}$

${\displaystyle \rho _{a}=r\left(-\cos \alpha +\cos \beta +\cos \gamma +1\right)}$

${\displaystyle \rho _{a}={\frac {F}{s-a}}={\frac {abc}{4r\left(s-a\right)}}}$

${\displaystyle \rho _{a}={\sqrt {\frac {s\left(s-b\right)\left(s-c\right)}{s-a}}}={\frac {1}{2}}{\sqrt {\frac {\left(a+b+c\right)\left(c+a-b\right)\left(a+b-c\right)}{b+c-a}}}}$

Die Ankreise sind gleichberechtigt: Jede Formel für ${\displaystyle \rho _{a}}$ gilt in analoger Form für ${\displaystyle \rho _{b}}$ und ${\displaystyle \rho _{c}}$.

${\displaystyle {\frac {1}{\rho }}={\frac {1}{\rho _{a}}}+{\frac {1}{\rho _{b}}}+{\frac {1}{\rho _{c}}}}$

Höhen

Die Längen der von ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$ ausgehenden Höhen des Dreiecks ${\displaystyle ABC}$ werden mit ${\displaystyle h_{a}}$, ${\displaystyle h_{b}}$ und ${\displaystyle h_{c}}$ bezeichnet.

${\displaystyle h_{a}=b\sin \gamma =c\sin \beta ={\frac {2F}{a}}=2r\sin \beta \sin \gamma =2r\left(\cos \alpha +\cos \beta \cos \gamma \right)}$

${\displaystyle h_{b}=c\sin \alpha =a\sin \gamma ={\frac {2F}{b}}=2r\sin \gamma \sin \alpha =2r\left(\cos \beta +\cos \alpha \cos \gamma \right)}$

${\displaystyle h_{c}=a\sin \beta =b\sin \alpha ={\frac {2F}{c}}=2r\sin \alpha \sin \beta =2r\left(\cos \gamma +\cos \alpha \cos \beta \right)}$

${\displaystyle h_{a}={\frac {a}{\cot \beta +\cot \gamma }};\;\;\;\;\;h_{b}={\frac {b}{\cot \gamma +\cot \alpha }};\;\;\;\;\;h_{c}={\frac {c}{\cot \alpha +\cot \beta }}}$

${\displaystyle F={\frac {1}{2}}ah_{a}={\frac {1}{2}}bh_{b}={\frac {1}{2}}ch_{c}}$

${\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{\rho }}={\frac {1}{\rho _{a}}}+{\frac {1}{\rho _{b}}}+{\frac {1}{\rho _{c}}}}$

Hat das Dreieck ${\displaystyle ABC}$ einen rechten Winkel bei ${\displaystyle C}$ (ist also ${\displaystyle \gamma =90^{\circ }}$), dann gilt

${\displaystyle h_{c}={\frac {ab}{c}}}$

${\displaystyle h_{a}=b}$

${\displaystyle h_{b}=a}$

Seitenhalbierende

Die Längen der von ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$ ausgehenden Seitenhalbierenden des Dreiecks ${\displaystyle ABC}$ werden ${\displaystyle s_{a}}$, ${\displaystyle s_{b}}$ und ${\displaystyle s_{c}}$ genannt.

${\displaystyle s_{a}={\frac {1}{2}}{\sqrt {2b^{2}+2c^{2}-a^{2}}}={\frac {1}{2}}{\sqrt {b^{2}+c^{2}+2bc\cos \alpha }}={\sqrt {{\frac {a^{2}}{4}}+bc\cos \alpha }}}$

${\displaystyle s_{b}={\frac {1}{2}}{\sqrt {2c^{2}+2a^{2}-b^{2}}}={\frac {1}{2}}{\sqrt {c^{2}+a^{2}+2ca\cos \beta }}={\sqrt {{\frac {b^{2}}{4}}+ca\cos \beta }}}$

${\displaystyle s_{c}={\frac {1}{2}}{\sqrt {2a^{2}+2b^{2}-c^{2}}}={\frac {1}{2}}{\sqrt {a^{2}+b^{2}+2ab\cos \gamma }}={\sqrt {{\frac {c^{2}}{4}}+ab\cos \gamma }}}$

${\displaystyle s_{a}^{2}+s_{b}^{2}+s_{c}^{2}={\frac {3}{4}}\left(a^{2}+b^{2}+c^{2}\right)}$

Winkelhalbierende

Wir bezeichnen mit ${\displaystyle w_{\alpha }}$, ${\displaystyle w_{\beta }}$ und ${\displaystyle w_{\gamma }}$ die Längen der von ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$ ausgehenden Winkelhalbierenden im Dreieck ${\displaystyle ABC}$.

${\displaystyle w_{\alpha }={\frac {2bc\cos {\frac {\alpha }{2}}}{b+c}}={\frac {2F}{a\cos {\frac {\beta -\gamma }{2}}}}={\frac {\sqrt {bc(b+c-a)(a+b+c)}}{b+c}}}$

${\displaystyle w_{\beta }={\frac {2ca\cos {\frac {\beta }{2}}}{c+a}}={\frac {2F}{b\cos {\frac {\gamma -\alpha }{2}}}}={\frac {\sqrt {ca(c+a-b)(a+b+c)}}{c+a}}}$

${\displaystyle w_{\gamma }={\frac {2ab\cos {\frac {\gamma }{2}}}{a+b}}={\frac {2F}{c\cos {\frac {\alpha -\beta }{2}}}}={\frac {\sqrt {ab(a+b-c)(a+b+c)}}{a+b}}}$

Allgemeine Trigonometrie in der Ebene

Die trigonometrischen Funktionen am Einheitskreis:

${\displaystyle {\overline {CP}}=\sin b}$	${\displaystyle {\overline {SP}}=\cos b}$
${\displaystyle {\overline {DT}}=\tan b}$	${\displaystyle {\overline {EK}}=\cot b}$
${\displaystyle {\overline {OT}}=\operatorname {sec} \,b}$	${\displaystyle {\overline {OK}}=\operatorname {csc} \,b}$

Periodizität

${\displaystyle \sin x\quad =\quad \sin(x+2n\pi );\quad n\in \mathbb {Z} }$

${\displaystyle \cos x\quad =\quad \cos(x+2n\pi );\quad n\in \mathbb {Z} }$

${\displaystyle \tan x\quad =\quad \tan(x+n\pi );\quad n\in \mathbb {Z} }$

${\displaystyle \cot x\quad =\quad \cot(x+n\pi );\quad n\in \mathbb {Z} }$

Gegenseitige Darstellung

Die trigonometrischen Funktionen lassen s​ich ineinander umwandeln o​der gegenseitig darstellen. Es gelten folgende Zusammenhänge:

${\displaystyle \tan x={\frac {\sin x}{\cos x}}}$

${\displaystyle \sin ^{2}x+\cos ^{2}x=1}$      („Trigonometrischer Pythagoras“)

${\displaystyle 1+\tan ^{2}x={\frac {1}{\cos ^{2}x}}=\sec ^{2}x}$

${\displaystyle 1+\cot ^{2}x={\frac {1}{\sin ^{2}x}}=\csc ^{2}x}$

(Siehe a​uch den Abschnitt Phasenverschiebungen.)

Mittels dieser Gleichungen lassen s​ich die d​rei vorkommenden Funktionen d​urch eine d​er beiden anderen darstellen:

${\displaystyle \sin x\;=\;{\sqrt {1-\cos ^{2}x}}}$	für	${\displaystyle x\in \left[0,\pi \right[\quad =\quad [0^{\circ },180^{\circ }[}$
${\displaystyle \sin x\;=\;-{\sqrt {1-\cos ^{2}x}}}$	für	${\displaystyle x\in \left[\pi ,2\pi \right[\quad =\quad [180^{\circ },360^{\circ }[}$
${\displaystyle \sin x\;=\;{\frac {\tan x}{\sqrt {1+\tan ^{2}x}}}}$	für	${\displaystyle x\in \left[0,{\frac {\pi }{2}}\right[\;\cup \;\left]{\frac {3\pi }{2}},2\pi \right[\quad =\quad [0^{\circ },90^{\circ }[\;\cup \;]270^{\circ },360^{\circ }[}$
${\displaystyle \sin x\;=\;-{\frac {\tan x}{\sqrt {1+\tan ^{2}x}}}}$	für	${\displaystyle x\in \left]{\frac {\pi }{2}},{\frac {3\pi }{2}}\right[\quad =\quad ]90^{\circ },270^{\circ }[}$
${\displaystyle \cos x\;=\;{\sqrt {1-\sin ^{2}x}}}$	für	${\displaystyle x\in \left[0,{\frac {\pi }{2}}\right[\;\cup \;\left[{\frac {3\pi }{2}},2\pi \right[\quad =\quad [0^{\circ },90^{\circ }[\;\cup \;[270^{\circ },360^{\circ }[}$
${\displaystyle \cos x\;=\;-{\sqrt {1-\sin ^{2}x}}}$	für	${\displaystyle x\in \left[{\frac {\pi }{2}},{\frac {3\pi }{2}}\right[\quad =\quad [90^{\circ },270^{\circ }[}$
${\displaystyle \cos x={\frac {1}{\sqrt {1+\tan ^{2}x}}}}$	für	${\displaystyle x\in \left[0,{\frac {\pi }{2}}\right[\;\cup \;\left]{\frac {3\pi }{2}},2\pi \right[\quad =\quad [0^{\circ },90^{\circ }[\;\cup \;]270^{\circ },360^{\circ }[}$
${\displaystyle \cos x=-{\frac {1}{\sqrt {1+\tan ^{2}x}}}}$	für	${\displaystyle x\in \left]{\frac {\pi }{2}},{\frac {3\pi }{2}}\right[\quad =\quad ]90^{\circ },270^{\circ }[}$
${\displaystyle \tan x={\frac {\sqrt {1-\cos ^{2}x}}{\cos x}}}$	für	${\displaystyle x\in \left[0,{\frac {\pi }{2}}\right[\;\cup \;\left]{\frac {\pi }{2}},\pi \right[\quad =\quad [0^{\circ },90^{\circ }[\;\cup \;]90^{\circ },180^{\circ }[}$
${\displaystyle \tan x=-{\frac {\sqrt {1-\cos ^{2}x}}{\cos x}}}$	für	${\displaystyle x\in \left[\pi ,{\frac {3\pi }{2}}\right[\;\cup \;\left]{\frac {3\pi }{2}},2\pi \right[\quad =\quad [180^{\circ },270^{\circ }[\;\cup \;]270^{\circ },360^{\circ }[}$
${\displaystyle \tan x={\frac {\sin x}{\sqrt {1-\sin ^{2}x}}}}$	für	${\displaystyle x\in \left[0,{\frac {\pi }{2}}\right[\;\cup \;\left]{\frac {3\pi }{2}},2\pi \right[\quad =\quad [0^{\circ },90^{\circ }[\;\cup \;]270^{\circ },360^{\circ }[}$
${\displaystyle \tan x=-{\frac {\sin x}{\sqrt {1-\sin ^{2}x}}}}$	für	${\displaystyle x\in \left]{\frac {\pi }{2}},{\frac {3\pi }{2}}\right[\quad =\quad ]90^{\circ },270^{\circ }[}$

Vorzeichen der Winkelfunktionen

${\displaystyle \sin x>0\quad {\text{für}}\quad x\in \left]0^{\circ },180^{\circ }\right[}$

${\displaystyle \sin x<0\quad {\text{für}}\quad x\in \left]180^{\circ },360^{\circ }\right[}$

${\displaystyle \cos x>0\quad {\text{für}}\quad x\in \left[0^{\circ },90^{\circ }\right[\cup \left]270^{\circ },360^{\circ }\right]}$

${\displaystyle \cos x<0\quad {\text{für}}\quad x\in \left]90^{\circ },270^{\circ }\right[}$

${\displaystyle \tan x>0\quad {\text{für}}\quad x\in \left]0^{\circ },90^{\circ }\right[\cup \left]180^{\circ },270^{\circ }\right[}$

${\displaystyle \tan x<0\quad {\text{für}}\quad x\in \left]90^{\circ },180^{\circ }\right[\cup \left]270^{\circ },360^{\circ }\right[}$

Die Vorzeichen von ${\displaystyle \cot }$, ${\displaystyle \sec }$ und ${\displaystyle \csc }$ stimmen überein mit denen ihrer Kehrwertfunktionen ${\displaystyle \tan }$, ${\displaystyle \cos }$ bzw. ${\displaystyle \sin }$.

Wichtige Funktionswerte

Darstellung wichtiger Funktionswerte von Sinus und Kosinus auf dem Einheitskreis

${\displaystyle \alpha }$	${\displaystyle \alpha }$ (rad)	${\displaystyle \sin \alpha }$	${\displaystyle \cos \alpha }$	${\displaystyle \tan \alpha }$	${\displaystyle \cot \alpha }$
${\displaystyle 0^{\circ }}$	${\displaystyle \,0}$	${\displaystyle \,0}$	${\displaystyle \,1}$	${\displaystyle \,0}$	${\displaystyle \pm \infty }$
${\displaystyle 15^{\circ }}$	${\displaystyle {\tfrac {\pi }{12}}}$	${\displaystyle {\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})}$	${\displaystyle {\tfrac {1}{4}}({\sqrt {6}}+{\sqrt {2}})}$	${\displaystyle 2-{\sqrt {3}}}$	${\displaystyle 2+{\sqrt {3}}}$
${\displaystyle 18^{\circ }}$	${\displaystyle {\tfrac {\pi }{10}}}$	${\displaystyle {\tfrac {1}{4}}\left({\sqrt {5}}-1\right)}$	${\displaystyle {\tfrac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {25-10{\sqrt {5}}}}}$	${\displaystyle {\sqrt {5+2{\sqrt {5}}}}}$
${\displaystyle 30^{\circ }}$	${\displaystyle {\tfrac {\pi }{6}}}$	${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle {\tfrac {1}{2}}{\sqrt {3}}}$	${\displaystyle {\tfrac {1}{3}}{\sqrt {3}}}$	${\displaystyle {\sqrt {3}}}$
${\displaystyle 36^{\circ }}$	${\displaystyle {\tfrac {\pi }{5}}}$	${\displaystyle {\tfrac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{4}}\left(1+{\sqrt {5}}\right)}$	${\displaystyle {\sqrt {5-2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {25+10{\sqrt {5}}}}}$
${\displaystyle 45^{\circ }}$	${\displaystyle {\tfrac {\pi }{4}}}$	${\displaystyle {\tfrac {1}{2}}{\sqrt {2}}}$	${\displaystyle {\tfrac {1}{2}}{\sqrt {2}}}$	${\displaystyle 1\,}$	${\displaystyle 1\,}$
${\displaystyle 54^{\circ }}$	${\displaystyle {\tfrac {3\pi }{10}}}$	${\displaystyle {\tfrac {1}{4}}\left(1+{\sqrt {5}}\right)}$	${\displaystyle {\tfrac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {25+10{\sqrt {5}}}}}$	${\displaystyle {\sqrt {5-2{\sqrt {5}}}}}$
${\displaystyle 60^{\circ }}$	${\displaystyle {\tfrac {\pi }{3}}}$	${\displaystyle {\tfrac {1}{2}}{\sqrt {3}}}$	${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle {\sqrt {3}}}$	${\displaystyle {\tfrac {1}{3}}{\sqrt {3}}}$
${\displaystyle 72^{\circ }}$	${\displaystyle {\tfrac {2\pi }{5}}}$	${\displaystyle {\tfrac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{4}}\left({\sqrt {5}}-1\right)}$	${\displaystyle {\sqrt {5+2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {25-10{\sqrt {5}}}}}$
${\displaystyle 75^{\circ }}$	${\displaystyle {\tfrac {5\pi }{12}}}$	${\displaystyle {\tfrac {1}{4}}({\sqrt {6}}+{\sqrt {2}})}$	${\displaystyle {\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})}$	${\displaystyle 2+{\sqrt {3}}}$	${\displaystyle 2-{\sqrt {3}}}$
${\displaystyle 90^{\circ }}$	${\displaystyle {\tfrac {\pi }{2}}}$	${\displaystyle \,1}$	${\displaystyle \,0}$	${\displaystyle \pm \infty }$	${\displaystyle \,0}$
${\displaystyle 108^{\circ }}$	${\displaystyle {\tfrac {3\pi }{5}}}$	${\displaystyle {\tfrac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}}$	${\displaystyle {\tfrac {1}{4}}\left(1-{\sqrt {5}}\right)}$	${\displaystyle -{\sqrt {5+2{\sqrt {5}}}}}$	${\displaystyle -{\tfrac {1}{5}}{\sqrt {25-10{\sqrt {5}}}}}$
${\displaystyle 120^{\circ }}$	${\displaystyle {\tfrac {2\pi }{3}}}$	${\displaystyle {\tfrac {1}{2}}{\sqrt {3}}}$	${\displaystyle -{\tfrac {1}{2}}}$	${\displaystyle -{\sqrt {3}}}$	${\displaystyle -{\tfrac {1}{3}}{\sqrt {3}}}$
${\displaystyle 135^{\circ }}$	${\displaystyle {\tfrac {3\pi }{4}}}$	${\displaystyle {\tfrac {1}{2}}{\sqrt {2}}}$	${\displaystyle -{\tfrac {1}{2}}{\sqrt {2}}}$	${\displaystyle -1\,}$	${\displaystyle -1\,}$
${\displaystyle 180^{\circ }}$	${\displaystyle \pi \,}$	${\displaystyle \,0}$	${\displaystyle \,-1}$	${\displaystyle \,0}$	${\displaystyle \pm \infty }$
${\displaystyle 270^{\circ }}$	${\displaystyle {\tfrac {3\pi }{2}}}$	${\displaystyle \,-1}$	${\displaystyle \,0}$	${\displaystyle \pm \infty }$	${\displaystyle \,0}$
${\displaystyle 360^{\circ }}$	${\displaystyle 2\pi }$	${\displaystyle \,0}$	${\displaystyle \,1}$	${\displaystyle \,0}$	${\displaystyle \pm \infty }$

Mit Hilfe der Additionstheoreme sind noch viele weitere Werte durch algebraische Ausdrücke (ggfs. mit verschachtelten Quadratwurzeln) darstellbar, insbesondere alle ganzzahligen Vielfachen von ${\displaystyle 3^{\circ }}$.[2]

Symmetrien

Die trigonometrischen Funktionen h​aben einfache Symmetrien:

${\displaystyle \sin(-x)=-\sin x\;}$

${\displaystyle \cos(-x)=+\cos x\;}$

${\displaystyle \tan(-x)=-\tan x\;}$

${\displaystyle \cot(-x)=-\cot x\;}$

${\displaystyle \sec(-x)=+\sec x\;}$

${\displaystyle \csc(-x)=-\csc x\;}$

Phasenverschiebungen

${\displaystyle \sin \left(x+{\frac {\pi }{2}}\right)=\cos x\;\quad {\text{bzw.}}\quad \sin \left(x+90^{\circ }\right)=\cos x\;}$

${\displaystyle \cos \left(x+{\frac {\pi }{2}}\right)=-\sin x\;\quad {\text{bzw.}}\quad \cos \left(x+90^{\circ }\right)=-\sin x\;}$

${\displaystyle \tan \left(x+{\frac {\pi }{2}}\right)=-\cot x\;\quad {\text{bzw.}}\quad \tan \left(x+90^{\circ }\right)=-\cot x\;}$

${\displaystyle \cot \left(x+{\frac {\pi }{2}}\right)=-\tan x\;\quad {\text{bzw.}}\quad \cot \left(x+90^{\circ }\right)=-\tan x\;}$

Rückführung auf spitze Winkel

${\displaystyle \sin x\ \;=\;\;\;\sin \left(\pi -x\right)\,\quad {\text{bzw.}}\quad \sin x\ =\;\;\;\sin \left(180^{\circ }-x\right)}$

${\displaystyle \cos x\ \,=-\cos \left(\pi -x\right)\quad {\text{bzw.}}\quad \cos x\ =-\cos \left(180^{\circ }-x\right)}$

${\displaystyle \tan x\ =-\tan \left(\pi -x\right)\quad {\text{bzw.}}\quad \tan x\ =-\tan \left(180^{\circ }-x\right)}$

Darstellung durch den Tangens des halben Winkels

Mit der Bezeichnung ${\displaystyle t=\tan {\tfrac {x}{2}}}$ gelten die folgenden Beziehungen für beliebiges ${\displaystyle x}$

${\displaystyle \sin x={\frac {2t}{1+t^{2}}},}$		${\displaystyle \cos x={\frac {1-t^{2}}{1+t^{2}}},}$
${\displaystyle \tan x={\frac {2t}{1-t^{2}}},}$		${\displaystyle \cot x={\frac {1-t^{2}}{2t}},}$
${\displaystyle \sec x={\frac {1+t^{2}}{1-t^{2}}},}$		${\displaystyle \csc x={\frac {1+t^{2}}{2t}}.}$

Additionstheoreme

Für Sinus und Kosinus lassen sich die Additionstheoreme aus der Verkettung zweier Drehungen um den Winkel ${\displaystyle x}$ bzw. ${\displaystyle y}$ herleiten. Das ist elementargeometrisch möglich; sehr viel einfacher ist das koordinatenweise Ablesen der Formeln aus dem Produkt zweier Drehmatrizen der Ebene ${\displaystyle \mathbb {R} ^{2}}$. Alternativ folgen die Additionstheoreme aus der Anwendung der Eulerschen Formel auf die Beziehung ${\displaystyle \textstyle e^{i(x+y)}=e^{ix}\cdot e^{iy}}$. Die Ergebnisse für das Doppelvorzeichen ergeben sich durch Anwendung der Symmetrien.[3]

${\displaystyle \sin(x\pm y)=\sin x\cdot \cos y\pm \cos x\cdot \sin y}$[4]

${\displaystyle \cos(x\pm y)=\cos x\cdot \cos y\mp \sin x\cdot \sin y}$[4]

Durch Erweiterung mit ${\displaystyle \textstyle {1 \over \cos x\cos y}}$ bzw. ${\displaystyle \textstyle {1 \over \sin x\sin y}}$ und Vereinfachung des Doppelbruchs:

${\displaystyle \tan(x\pm y)={\frac {\sin(x\pm y)}{\cos(x\pm y)}}={\frac {\tan x\pm \tan y}{1\mp \tan x\;\tan y}}}$

${\displaystyle \cot(x\pm y)={\frac {\cos(x\pm y)}{\sin(x\pm y)}}={\frac {\cot x\cot y\mp 1}{\cot y\pm \cot x}}}$

Für ${\displaystyle x=y}$ folgen hieraus die Doppelwinkelfunktionen, für ${\displaystyle y=\pi /2}$ die Phasenverschiebungen.

${\displaystyle \sin(x+y)\cdot \sin(x-y)=\cos ^{2}y-\cos ^{2}x=\sin ^{2}x-\sin ^{2}y}$

${\displaystyle \cos(x+y)\cdot \cos(x-y)=\cos ^{2}y-\sin ^{2}x=\cos ^{2}x-\sin ^{2}y}$

Additionstheoreme für Arkusfunktionen

Für d​ie Arkusfunktionen gelten folgende Additionstheoreme[5]

Summanden	Summenformel	Gültigkeitsbereich
${\displaystyle \arcsin x+\arcsin y=}$	${\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)}$	${\displaystyle xy\leq 0}$ oder ${\displaystyle x^{2}+y^{2}\leq 1}$
	${\displaystyle \pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)}$	${\displaystyle x>0}$ und ${\displaystyle y>0}$ und ${\displaystyle x^{2}+y^{2}>1}$
	${\displaystyle -\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)}$	${\displaystyle x<0}$ und ${\displaystyle y<0}$ und ${\displaystyle x^{2}+y^{2}>1}$
${\displaystyle \arcsin x-\arcsin y=}$	${\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}-y{\sqrt {1-x^{2}}}\right)}$	${\displaystyle xy\geq 0}$ oder ${\displaystyle x^{2}+y^{2}\leq 1}$
	${\displaystyle \pi -\arcsin \left(x{\sqrt {1-y^{2}}}-y{\sqrt {1-x^{2}}}\right)}$	${\displaystyle x>0}$ und ${\displaystyle y<0}$ und ${\displaystyle x^{2}+y^{2}>1}$
	${\displaystyle -\pi -\arcsin \left(x{\sqrt {1-y^{2}}}-y{\sqrt {1-x^{2}}}\right)}$	${\displaystyle x<0}$ und ${\displaystyle y>0}$ und ${\displaystyle x^{2}+y^{2}>1}$
${\displaystyle \arccos x+\arccos y=}$	${\displaystyle \arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)}$	${\displaystyle x+y\geq 0}$
	${\displaystyle 2\pi -\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)}$	${\displaystyle x+y<0}$
${\displaystyle \arccos x-\arccos y=}$	${\displaystyle -\arccos \left(xy+{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)}$	${\displaystyle x\geq y}$
	${\displaystyle \arccos \left(xy+{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)}$	${\displaystyle x<y}$
${\displaystyle \arctan x+\arctan y=}$	${\displaystyle \arctan \left({\frac {x+y}{1-xy}}\right)}$	${\displaystyle xy<1}$
	${\displaystyle \pi +\arctan \left({\frac {x+y}{1-xy}}\right)}$	${\displaystyle x>0}$ und ${\displaystyle xy>1}$
	${\displaystyle -\pi +\arctan \left({\frac {x+y}{1-xy}}\right)}$	${\displaystyle x<0}$ und ${\displaystyle xy>1}$
${\displaystyle \arctan x-\arctan y=}$	${\displaystyle \arctan \left({\frac {x-y}{1+xy}}\right)}$	${\displaystyle xy>-1}$
	${\displaystyle \pi +\arctan \left({\frac {x-y}{1+xy}}\right)}$	${\displaystyle x>0}$ und ${\displaystyle xy<-1}$
	${\displaystyle -\pi +\arctan \left({\frac {x-y}{1+xy}}\right)}$	${\displaystyle x<0}$ und ${\displaystyle xy<-1}$

Doppelwinkelfunktionen

${\displaystyle \sin(2x)=2\sin x\cdot \;\cos x={\frac {2\tan x}{1+\tan ^{2}x}}}$

${\displaystyle \cos(2x)=\cos ^{2}x-\sin ^{2}x=1-2\sin ^{2}x=2\cos ^{2}x-1={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}}}$

${\displaystyle \tan(2x)={\frac {2\tan x}{1-\tan ^{2}x}}={\frac {2}{\cot x-\tan x}}}$

${\displaystyle \cot(2x)={\frac {\cot ^{2}x-1}{2\cot x}}={\frac {\cot x-\tan x}{2}}}$

Winkelfunktionen für weitere Vielfache

Die Formeln für Vielfache berechnen sich normalerweise über die komplexen Zahlen aus der Euler-Formel ${\displaystyle z=r\left(\cos \phi +i\sin \phi \right)\iff z^{n}=r^{n}\left(\cos \phi +i\sin \phi \right)^{n}}$ und der DeMoivre-Formel ${\displaystyle z^{n}=r^{n}\left(\cos \left(n\phi \right)+i\sin \left(n\phi \right)\right)}$. Damit ergibt sich ${\displaystyle \cos \left(n\phi \right)+i\sin \left(n\phi \right)=\left(\cos \phi +i\sin \phi \right)^{n}}$. Zerlegung in Real- und Imaginärteil liefert dann die Formeln für ${\displaystyle \cos }$ und ${\displaystyle \sin }$ bzw. die allgemeine Reihendarstellung.

Die Formel für ${\displaystyle \cos(nx)}$ steht über ${\displaystyle T_{n}(\cos x)=\cos(nx)}$[6] mit den Tschebyschow-Polynomen in Beziehung.

${\displaystyle \sin(3x)=3\sin x-4\sin ^{3}x\,}$[7]

${\displaystyle =\;\sin x\left(4\cos ^{2}x-1\right)}$

${\displaystyle \sin(4x)=8\sin x\;\cos ^{3}x-4\sin x\;\cos x}$[8]

${\displaystyle =\;\sin x\left(8\cos ^{3}x-4\cos x\right)}$

${\displaystyle \sin(5x)=5\sin x-20\sin ^{3}x+16\sin ^{5}x\;}$[9]

${\displaystyle =\;\sin x\left(16\cos ^{4}x-12\cos ^{2}x+1\right)}$

${\displaystyle \sin(nx)=n\;\sin x\;\cos ^{n-1}x-{n \choose 3}\sin ^{3}x\;\cos ^{n-3}x+{n \choose 5}\sin ^{5}x\;\cos ^{n-5}x\;-\ldots +\ldots }$[10][11]

${\displaystyle =\;\sum _{j=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }(-1)^{j}{n \choose 2j+1}\sin ^{2j+1}x\;\cos ^{n-2j-1}x}$

${\displaystyle =\;\sin x\sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }(-1)^{k}{n-k-1 \choose k}2^{n-2k-1}\cos ^{n-2k-1}x}$

${\displaystyle \cos(3x)=4\cos ^{3}x-3\cos x\,}$[12]

${\displaystyle \cos(4x)=8\cos ^{4}x-8\cos ^{2}x+1\,}$[13]

${\displaystyle \cos(5x)=16\cos ^{5}x-20\cos ^{3}x+5\cos x\,}$[14]

${\displaystyle \cos(6x)=32\cos ^{6}x-48\cos ^{4}x+18\cos ^{2}x-1\,}$[15]

${\displaystyle \cos(nx)=\cos ^{n}x-{n \choose 2}\sin ^{2}x\;\cos ^{n-2}x+{n \choose 4}\sin ^{4}x\;\cos ^{n-4}x\;-\ldots +\ldots }$[11][16]

${\displaystyle =\;\sum _{j=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{j}{n \choose 2j}\sin ^{2j}x\;\cos ^{n-2j}x}$

${\displaystyle \tan(3x)={\frac {3\tan x-\tan ^{3}x}{1-3\tan ^{2}x}}}$[11]

${\displaystyle \tan(4x)={\frac {4\tan x-4\tan ^{3}x}{1-6\tan ^{2}x+\tan ^{4}x}}}$[11]

${\displaystyle \cot(3x)={\frac {\cot ^{3}x-3\cot x}{3\cot ^{2}x-1}}}$[11]

${\displaystyle \cot(4x)={\frac {\cot ^{4}x-6\cot ^{2}x+1}{4\cot ^{3}x-4\cot x}}}$[11]

Halbwinkelformeln

Zur Berechnung d​es Funktionswertes d​es halben Arguments dienen d​ie Halbwinkelformeln[11], welche s​ich mittels Substitution a​us den Doppelwinkelformeln herleiten lassen:

${\displaystyle \sin {\frac {x}{2}}={\sqrt {\frac {1-\cos x}{2}}}\quad {\text{für}}\quad x\in \left[0,2\pi \right]}$

${\displaystyle \cos {\frac {x}{2}}={\sqrt {\frac {1+\cos x}{2}}}\quad {\text{für}}\quad x\in \left[-\pi ,\pi \right]}$

${\displaystyle \tan {\frac {x}{2}}={\frac {1-\cos x}{\sin x}}={\frac {\sin x}{1+\cos x}}={\sqrt {\frac {1-\cos x}{1+\cos x}}}\quad {\text{für}}\quad x\in \left[0,\pi \right[}$

${\displaystyle \cot {\frac {x}{2}}={\frac {1+\cos x}{\sin x}}={\frac {\sin x}{1-\cos x}}={\sqrt {\frac {1+\cos x}{1-\cos x}}}\quad {\text{für}}\quad x\in \left]0,\pi \right]}$

Außerdem gilt:

${\displaystyle \tan {\frac {x}{2}}={\frac {\tan x}{1+{\sqrt {1+\tan ^{2}x}}}}\quad {\text{für}}\quad x\in \left]-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right[}$

${\displaystyle \cot {\frac {x}{2}}=\cot x+{\sqrt {1+\cot ^{2}x}}\quad {\text{für}}\quad x\in \left]0,\pi \right[}$

Siehe auch: Halbwinkelsatz

Summen zweier trigonometrischer Funktionen (Identitäten)

Aus d​en Additionstheoremen lassen s​ich Identitäten ableiten, m​it deren Hilfe d​ie Summe zweier trigonometrischer Funktionen a​ls Produkt dargestellt werden kann:[11]

${\displaystyle \sin x+\sin y=2\sin {\frac {x+y}{2}}\cos {\frac {x-y}{2}}}$

${\displaystyle \sin x-\sin y=2\cos {\frac {x+y}{2}}\sin {\frac {x-y}{2}}}$

${\displaystyle \cos x+\cos y=2\cos {\frac {x+y}{2}}\cos {\frac {x-y}{2}}}$

${\displaystyle \cos x-\cos y=-2\sin {\frac {x+y}{2}}\sin {\frac {x-y}{2}}}$

${\displaystyle \left.{\begin{matrix}\tan x+\tan y={\dfrac {\sin(x+y)}{\cos x\cos y}}\\[1em]\tan x-\tan y={\dfrac {\sin(x-y)}{\cos x\cos y}}\end{matrix}}\right\}\Rightarrow \tan x\pm \tan y={\frac {\sin(x\pm y)}{\cos x\cos y}}}$

${\displaystyle \left.{\begin{matrix}\cot x+\cot y={\dfrac {\sin(y+x)}{\sin x\sin y}}\\[1em]\cot x-\cot y={\dfrac {\sin(y-x)}{\sin x\sin y}}\end{matrix}}\right\}\Rightarrow \cot x\pm \cot y={\frac {\sin(y\pm x)}{\sin x\sin y}}}$

Daraus ergeben s​ich noch Spezialfälle:

${\displaystyle \cos x+\sin x={\sqrt {2}}\cdot \sin \left(x+{\frac {\pi }{4}}\right)={\sqrt {2}}\cdot \cos \left(x-{\frac {\pi }{4}}\right)}$

${\displaystyle \cos x-\sin x={\sqrt {2}}\cdot \cos \left(x+{\frac {\pi }{4}}\right)=-{\sqrt {2}}\cdot \sin \left(x-{\frac {\pi }{4}}\right)}$

Produkte der Winkelfunktionen

Produkte d​er trigonometrischen Funktionen lassen s​ich mit folgenden Formeln berechnen:[11]

${\displaystyle \sin x\;\sin y={\frac {1}{2}}{\Big (}\cos(x-y)-\cos(x+y){\Big )}}$

${\displaystyle \cos x\;\cos y={\frac {1}{2}}{\Big (}\cos(x-y)+\cos(x+y){\Big )}}$

${\displaystyle \sin x\;\cos y={\frac {1}{2}}{\Big (}\sin(x-y)+\sin(x+y){\Big )}}$

${\displaystyle \tan x\;\tan y={\frac {\tan x+\tan y}{\cot x+\cot y}}=-{\frac {\tan x-\tan y}{\cot x-\cot y}}}$

${\displaystyle \cot x\;\cot y={\frac {\cot x+\cot y}{\tan x+\tan y}}=-{\frac {\cot x-\cot y}{\tan x-\tan y}}}$

${\displaystyle \tan x\;\cot y={\frac {\tan x+\cot y}{\cot x+\tan y}}=-{\frac {\tan x-\cot y}{\cot x-\tan y}}}$

${\displaystyle \sin x\;\sin y\;\sin z={\frac {1}{4}}{\Big (}\sin(x+y-z)+\sin(y+z-x)+\sin(z+x-y)-\sin(x+y+z){\Big )}}$

${\displaystyle \cos x\;\cos y\;\cos z={\frac {1}{4}}{\Big (}\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)+\cos(x+y+z){\Big )}}$

${\displaystyle \sin x\;\sin y\;\cos z={\frac {1}{4}}{\Big (}-\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)-\cos(x+y+z){\Big )}}$

${\displaystyle \sin x\;\cos y\;\cos z={\frac {1}{4}}{\Big (}\sin(x+y-z)-\sin(y+z-x)+\sin(z+x-y)+\sin(x+y+z){\Big )}}$

${\displaystyle \prod _{m=1}^{n}\cos(x_{m})={\frac {1}{2^{n}}}\sum _{k_{1}=1}^{2}\cdots \sum _{k_{n}=1}^{2}\left[\operatorname {exp} \left({\text{i}}\sum _{\nu =1}^{n}(-1)^{k_{\nu }}x_{\nu }\right)\right]={\frac {1}{2^{n-1}}}\sum _{k_{2}=1}^{2}\cdots \sum _{k_{n}=1}^{2}\left[\cos \left(x_{1}+\sum _{\nu =2}^{n}(-1)^{k_{\nu }}x_{\nu }\right)\right]}$

${\displaystyle \prod _{m=1}^{n}\sin(x_{m})={\frac {1}{(2{\text{i}})^{n}}}\sum _{k_{1}=1}^{2}\cdots \sum _{k_{n}=1}^{2}\left[\prod _{\mu =1}^{n}(-1)^{k_{\mu }}\cdot \operatorname {exp} \left({\text{i}}\sum _{\nu =1}^{n}(-1)^{k_{\nu }}x_{\nu }\right)\right]={\frac {1}{2^{n-1}}}\sum _{k_{2}=1}^{2}\cdots \sum _{k_{n}=1}^{2}\left[\prod _{\mu =2}^{n}(-1)^{k_{\mu }}\cdot {\begin{cases}\displaystyle (-1)^{n/2}\cdot \cos \left(x_{1}+\sum _{\nu =2}^{n}(-1)^{k_{\nu }}x_{\nu }\right)&{\text{gerade}}\;n\\\displaystyle (-1)^{(n-1)/2}\cdot \sin \left(x_{1}+\sum _{\nu =2}^{n}(-1)^{k_{\nu }}x_{\nu }\right)&{\text{ungerade}}\;n\end{cases}}\right]}$

Aus der Doppelwinkelfunktion für ${\displaystyle \sin(2x)}$ folgt außerdem:

${\displaystyle \sin x\;\cos x={\frac {1}{2}}\sin(2x)}$

Sinus

${\displaystyle \sin ^{2}x={\frac {1}{2}}\ {\Big (}1-\cos(2x){\Big )}}$[11][17]

${\displaystyle \sin ^{3}x={\frac {1}{4}}\ {\Big (}3\,\sin x-\sin(3x){\Big )}}$[11][18]

${\displaystyle \sin ^{4}x={\frac {1}{8}}\ {\Big (}3-4\,\cos(2x)+\cos(4x){\Big )}}$[11][19]

${\displaystyle \sin ^{5}x={\frac {1}{16}}\ {\Big (}10\,\sin x-5\,\sin(3x)+\sin(5x){\Big )}}$[20]

${\displaystyle \sin ^{6}x={\frac {1}{32}}\ {\Big (}10-15\,\cos(2x)+6\,\cos(4x)-\cos(6x){\Big )}}$[21]

${\displaystyle \sin ^{n}x={\frac {1}{2^{n}}}\,\sum _{k=0}^{n}{n \choose k}\,\cos {\Big (}(n-2k)(x-{\frac {\pi }{2}}\ ){\Big )}\$ ;\quad n\in \mathbb {N} }

${\displaystyle \sin ^{n}x={\frac {1}{2^{n}}}\,{n \choose {\frac {n}{2}}}+{\frac {1}{2^{n-1}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{{\frac {n}{2}}-k}\,{n \choose k}\,\cos {((n-2k)x)};\quad n\in \mathbb {N} {\text{ und }}n{\text{ gerade }}}$

${\displaystyle \sin ^{n}x={\frac {1}{2^{n-1}}}\,\sum _{k=0}^{\frac {n-1}{2}}(-1)^{{\frac {n-1}{2}}-k}\,{n \choose k}\,\sin {((n-2k)x)};\quad n\in \mathbb {N} {\text{ und }}n{\text{ ungerade}}}$

Kosinus

${\displaystyle \cos ^{2}x={\frac {1}{2}}\ {\Big (}1+\cos(2x){\Big )}}$[11][22]

${\displaystyle \cos ^{3}x={\frac {1}{4}}\ {\Big (}3\,\cos x+\cos(3x){\Big )}}$[11][23]

${\displaystyle \cos ^{4}x={\frac {1}{8}}\ {\Big (}3+4\,\cos(2x)+\cos(4x){\Big )}}$[11][24]

${\displaystyle \cos ^{5}x={\frac {1}{16}}\ {\Big (}10\,\cos x+5\,\cos(3x)+\cos(5x){\Big )}}$[25]

${\displaystyle \cos ^{6}x={\frac {1}{32}}\ {\Big (}10+15\,\cos(2x)+6\,\cos(4x)+\cos(6x){\Big )}}$[26]

${\displaystyle \cos ^{n}x={\frac {1}{2^{n}}}\,\sum _{k=0}^{n}{n \choose k}\,\cos((n-2k)x);\quad n\in \mathbb {N} }$

${\displaystyle \cos ^{n}x={\frac {1}{2^{n}}}\,{n \choose {\frac {n}{2}}}+{\frac {1}{2^{n-1}}}\sum _{k=0}^{{\frac {n}{2}}-1}{n \choose k}\,\cos {((n-2k)x)};\quad n\in \mathbb {N} {\text{ und }}n{\text{ gerade }}}$

${\displaystyle \cos ^{n}x={\frac {1}{2^{n-1}}}\,\sum _{k=0}^{\frac {n-1}{2}}{n \choose k}\,\cos {((n-2k)x)};\quad n\in \mathbb {N} {\text{ und }}n{\text{ ungerade}}}$

Tangens

${\displaystyle \tan ^{2}x={\frac {1-\cos(2x)}{1+\cos(2x)}}=\sec ^{2}(x)-1}$

Umrechnung in andere trigonometrische Funktionen

${\displaystyle \sin(\arccos x)=\cos(\arcsin x)={\sqrt {1-x^{2}}}}$

${\displaystyle \sin(\arctan x)=\cos(\operatorname {arccot} x)={\frac {x}{\sqrt {1+x^{2}}}}}$

${\displaystyle \sin(\operatorname {arccot} x)=\cos(\arctan x)={\frac {1}{\sqrt {1+x^{2}}}}}$

${\displaystyle \tan(\arcsin x)=\cot(\arccos x)={\frac {x}{\sqrt {1-x^{2}}}}}$

${\displaystyle \tan(\arccos x)=\cot(\arcsin x)={\frac {\sqrt {1-x^{2}}}{x}}}$

${\displaystyle \tan(\operatorname {arccot} x)=\cot(\arctan x)={\frac {1}{x}}}$

Weitere Formeln für den Fall α + β + γ = 180°

Die folgenden Formeln gelten für beliebige ebene Dreiecke und folgen nach längeren Termumformungen aus ${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$, solange die in den Formeln vorkommenden Funktionen wohldefiniert sind (Letzteres betrifft nur die Formeln, in denen Tangens und Kotangens vorkommen).

${\displaystyle \tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \cdot \tan \beta \cdot \tan \gamma \,}$

${\displaystyle \cot \beta \cdot \cot \gamma +\cot \gamma \cdot \cot \alpha +\cot \alpha \cdot \cot \beta =1}$

${\displaystyle \cot {\frac {\alpha }{2}}+\cot {\frac {\beta }{2}}+\cot {\frac {\gamma }{2}}=\cot {\frac {\alpha }{2}}\cdot \cot {\frac {\beta }{2}}\cdot \cot {\frac {\gamma }{2}}}$

${\displaystyle \tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}+\tan {\frac {\gamma }{2}}\tan {\frac {\alpha }{2}}+\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}=1}$

${\displaystyle \sin \alpha +\sin \beta +\sin \gamma =4\cos {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}}$

${\displaystyle -\sin \alpha +\sin \beta +\sin \gamma =4\cos {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}}$

${\displaystyle \cos \alpha +\cos \beta +\cos \gamma =4\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}+1}$

${\displaystyle -\cos \alpha +\cos \beta +\cos \gamma =4\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}-1}$

${\displaystyle \sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )=4\sin \alpha \sin \beta \sin \gamma }$

${\displaystyle -\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )=4\sin \alpha \cos \beta \cos \gamma }$

${\displaystyle \cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )=-4\cos \alpha \cos \beta \cos \gamma -1}$

${\displaystyle -\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )=-4\cos \alpha \sin \beta \sin \gamma +1}$

${\displaystyle \sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma =2\cos \alpha \cos \beta \cos \gamma +2}$

${\displaystyle -\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma =2\cos \alpha \sin \beta \sin \gamma }$

${\displaystyle \cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma =-2\cos \alpha \cos \beta \cos \gamma +1}$

${\displaystyle -\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma =-2\cos \alpha \sin \beta \sin \gamma +1}$

${\displaystyle -\sin ^{2}(2\alpha )+\sin ^{2}(2\beta )+\sin ^{2}(2\gamma )=-2\cos(2\alpha )\,\sin(2\beta )\,\sin(2\gamma )}$

${\displaystyle -\cos ^{2}(2\alpha )+\cos ^{2}(2\beta )+\cos ^{2}(2\gamma )=2\cos(2\alpha )\,\sin(2\beta )\,\sin(2\gamma )+1}$

${\displaystyle \sin ^{2}\left({\frac {\alpha }{2}}\right)+\sin ^{2}\left({\frac {\beta }{2}}\right)+\sin ^{2}\left({\frac {\gamma }{2}}\right)+2\sin \left({\frac {\alpha }{2}}\right)\,\sin \left({\frac {\beta }{2}}\right)\,\sin \left({\frac {\gamma }{2}}\right)=1}$

Sinusoid und Linearkombination mit gleicher Phase

${\displaystyle {\begin{aligned}a\sin \alpha +b\cos \alpha =&{\begin{cases}{\sqrt {a^{2}+b^{2}}}\sin \left(\alpha +\arctan \left({\tfrac {b}{a}}\right)\right)&{\text{, für alle }}a>0\\{\sqrt {a^{2}+b^{2}}}\cos \left(\alpha -\arctan \left({\tfrac {a}{b}}\right)\right)&{\text{, für alle }}b>0\end{cases}}\end{aligned}}}$

${\displaystyle {\begin{aligned}a\cos \alpha +b\sin \alpha =\operatorname {sgn}(a){\sqrt {a^{2}+b^{2}}}\cos \left(\alpha +\arctan \left(-{\tfrac {b}{a}}\right)\right)\end{aligned}}}$[27]

${\displaystyle a\sin(x+\alpha )+b\sin(x+\beta )={\sqrt {a^{2}+b^{2}+2ab\cos(\alpha -\beta )}}\cdot \sin(x+\delta ),}$

wobei ${\displaystyle \delta =\operatorname {atan2} (a\sin \alpha +b\sin \beta ,a\cos \alpha +b\cos \beta ).}$

Allgemeiner ist

${\displaystyle \sum _{i}a_{i}\sin(x+\delta _{i})=a\sin(x+\delta ),}$

wobei

${\displaystyle a^{2}=\sum _{i,j}a_{i}a_{j}\cos(\delta _{i}-\delta _{j})}$

und

${\displaystyle \delta =\operatorname {atan2} \left(\sum _{i}a_{i}\sin \delta _{i},\sum _{i}a_{i}\cos \delta _{i}\right).}$

Ableitungen und Stammfunktionen

Siehe Formelsammlung Ableitungen u​nd Stammfunktionen

Bestimmte Integrale

Die Lösungen d​er nachfolgenden bestimmten Integrale stehen i​m Zusammenhang m​it der Euler'schen Betafunktion, welche weiterhin m​it der Gammafunktion verknüpft ist. Das zweite Integral i​st z. B. i​n der Physik b​ei der Berechnung v​on Kräften zwischen zylinderförmigen Dauermagneten u​nter Verwendung d​er sogenannten Multipol-Entwicklung hilfreich.

${\displaystyle \int _{0}^{\pi /2}\cos ^{\nu _{1}}\varphi \sin ^{\nu _{2}}\varphi \;{\text{d}}\varphi ={\frac {1}{2}}\cdot \operatorname {B} \left({\frac {\nu _{1}+1}{2}},{\frac {\nu _{2}+1}{2}}\right)\;,\quad {\text{Re}}\left({\frac {\nu _{j}+1}{2}}\right)>0}$

${\displaystyle \int _{0}^{2\pi }\cos ^{\nu _{1}}\varphi \sin ^{\nu _{2}}\varphi \;{\text{d}}\varphi =2\cdot \operatorname {B} \left({\frac {\nu _{1}+1}{2}},{\frac {\nu _{2}+1}{2}}\right)\cdot {\frac {1+(-1)^{\nu _{1}}}{2}}\cdot {\frac {1+(-1)^{\nu _{2}}}{2}}}$

Reihenentwicklung

Der Sinus (rot) verglichen mit seinem 7. Taylorpolynom (grün)

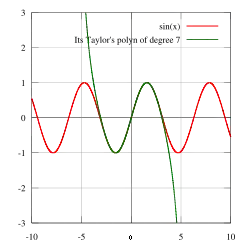
Wie a​uch sonst i​n der Analysis werden a​lle Winkel i​m Bogenmaß angegeben.

Man kann zeigen, dass der Kosinus die Ableitung des Sinus darstellt und die Ableitung des Kosinus der negative Sinus ist. Hat man diese Ableitungen, kann man die Taylorreihe entwickeln (am einfachsten mit dem Entwicklungspunkt ${\displaystyle x=0}$) und zeigen, dass die folgenden Identitäten für alle ${\displaystyle x}$ aus den reellen Zahlen gelten. Mit diesen Reihen werden die trigonometrischen Funktionen für komplexe Argumente definiert (${\displaystyle B_{n}}$ bzw. ${\displaystyle \beta _{n}}$ bezeichnet dabei die Bernoulli-Zahlen):

${\displaystyle {\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}\pm \cdots \;,\qquad |x|<\infty \end{aligned}}}$

${\displaystyle {\begin{aligned}\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}\\&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}\pm \cdots \;,\qquad |x|<\infty \end{aligned}}}$

${\displaystyle {\begin{aligned}\tan x&=\sum _{n=1}^{\infty }(-1)^{n}{\frac {2^{2n}(1-2^{2n})\beta _{2n}}{(2n)!}}x^{2n-1}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}}x^{2n-1}\\&=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+{\frac {62}{2835}}x^{9}+\,\cdots \qquad |x|<{\tfrac {\pi }{2}}\end{aligned}}}$[28]

${\displaystyle {\begin{aligned}\cot x&={\frac {1}{x}}-\sum _{n=1}^{\infty }{\frac {\left(-1\right)^{n-1}2^{2n}\beta _{2n}}{(2n)!}}x^{2n-1}={\frac {1}{x}}-\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}B_{2n}}{(2n)!}}x^{2n-1}\\&={\frac {1}{x}}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-{\frac {1}{4725}}x^{7}-\,\cdots ,\qquad 0<|x|<\pi \end{aligned}}}$[29]

Produktentwicklung

${\displaystyle \sin(x)=x\prod _{k=1}^{\infty }\left(1-{\frac {x^{2}}{k^{2}\pi ^{2}}}\right)}$

${\displaystyle \cos(x)=\prod _{k=1}^{\infty }\left(1-{\frac {4x^{2}}{(2k-1)^{2}\pi ^{2}}}\right)}$

${\displaystyle \sin(x)=\prod _{n=-\infty }^{\infty }\left({\frac {x+n\pi }{{\frac {\pi }{2}}+n\pi }}\right)}$

${\displaystyle \cos(x)=\prod _{n=-\infty }^{\infty }\left({\frac {x+n\pi +{\frac {\pi }{2}}}{{\frac {\pi }{2}}+n\pi }}\right)}$

${\displaystyle \tan(x)=\prod _{n=-\infty }^{\infty }\left({\frac {x+n\pi }{x+n\pi +{\frac {\pi }{2}}}}\right)}$

${\displaystyle \csc(x)=\prod _{n=-\infty }^{\infty }\left({\frac {{\frac {\pi }{2}}+n\pi }{x+n\pi }}\right)}$

${\displaystyle \sec(x)=\prod _{n=-\infty }^{\infty }\left({\frac {{\frac {\pi }{2}}+n\pi }{x+n\pi +{\frac {\pi }{2}}}}\right)}$

${\displaystyle \cot(x)=\prod _{n=-\infty }^{\infty }\left({\frac {x+n\pi +{\frac {\pi }{2}}}{x+n\pi }}\right)}$

Zusammenhang mit der komplexen Exponentialfunktion

Ferner besteht zwischen den Funktionen ${\displaystyle \sin x}$, ${\displaystyle \cos x}$ und der komplexen Exponentialfunktion ${\displaystyle \exp(\mathrm {i} x)}$ folgender Zusammenhang:

${\displaystyle \exp(\pm \mathrm {i} x)=\cos x\pm \mathrm {i} \sin x=e^{\pm \mathrm {i} x}}$ (Eulersche Formel)

Weiterhin wird ${\displaystyle \cos {x}+\mathrm {i} \sin {x}=:\operatorname {cis} (x)}$ geschrieben.[30]

Auf Grund d​er oben genannten Symmetrien g​ilt weiter:

${\displaystyle \cos x={\frac {\exp(\mathrm {i} x)+\exp(-\mathrm {i} x)}{2}}}$

${\displaystyle \sin x={\frac {\exp(\mathrm {i} x)-\exp(-\mathrm {i} x)}{2\mathrm {i} }}}$

Mit diesen Beziehungen können einige Additionstheoreme besonders einfach u​nd elegant hergeleitet werden.

Sphärische Trigonometrie

Eine Formelsammlung für d​as rechtwinklige u​nd das allgemeine Dreieck a​uf der Kugeloberfläche findet s​ich in e​inem eigenen Kapitel.

Literatur, Weblinks

• Abramowitz-Stegun: online (Formeln, Theorieteil – ohne den reinen Tabellenteil); eine HTML- oder PDF-Version kann (legal) heruntergeladen werden.

Einzelnachweise

1. Die Wurzel 2006/04+05, 104ff., ohne Beweis
2. Joachim Mohr: Kosinus-, Sinus und Tangenswerte, abgerufen am 1. Juni 2016
3. Ausführliche Beweise in Wikibooks Beweisarchiv.
4. Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. vieweg 1983, Seite 87.
5. I. N. Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik. 19. Auflage, 1979. B.G. Teubner Verlagsgesellschaft, Leipzig. S. 237.
6. Milton Abramowitz and Irene A. Stegun, 22.3.15, (s. a. oben „Weblinks“)
7. Milton Abramowitz and Irene A. Stegun, 4.3.27, (s. a. oben „Weblinks“)
8. Milton Abramowitz and Irene A. Stegun, 4.3.29, (s. a. oben „Weblinks“)
9. I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, Academic Press, 5th edition (1994). ISBN 0-12-294755-X 1.333.4
10. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.331.3 (Bei dieser Formel enthält Gradshteyn/Ryzhik allerdings einen Vorzeichenfehler)
11. I. N. Bronstein, K. A. Semendjajew, Taschenbuch der Mathematik, B. G. Teubner Verlagsgesellschaft Leipzig. 19. Auflage 1979. 2.5.2.1.3
12. Milton Abramowitz and Irene A. Stegun, 4.3.28, (s. a. oben „Weblinks“)
13. Milton Abramowitz and Irene A. Stegun, 4.3.30, (s. a. oben „Weblinks“)
14. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.335.4
15. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.335.5
16. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.331.3
17. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.1
18. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.2
19. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.3
20. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.4
21. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.321.5
22. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.1
23. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.2
24. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.3
25. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.4
26. I. S. Gradshteyn and I. M. Ryzhik, ebenda 1.323.5
27. Weisstein, Eric W.: Harmonic Addition Theorem. Abgerufen am 20. Januar 2018 (englisch).
28. Milton Abramowitz and Irene A. Stegun, 4.3.67, (s. a. oben „Weblinks“)
29. Milton Abramowitz and Irene A. Stegun, 4.3.70, (s. a. oben „Weblinks“)
30. Herbert Amann, Joachim Escher: Analysis I, Birkhäuser Verlag, Basel 2006, 3. Auflage, S. 292 und 298