Neuneck
Ein Neuneck oder Nonagon (seltener: Enneagon) ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone). Es ist definiert durch neun Punkte. Ein Polygon heißt regelmäßig, wenn es konvex ist, alle Seiten gleich lang sind und seine Eckpunkte auf einem gemeinsamen Umkreis liegen. Dieser Artikel beschäftigt sich im Weiteren ausschließlich mit regelmäßigen Neunecken (siehe Bild) und regelmäßigen überschlagenen Neunecken.
Mathematische Zusammenhänge
Formel für Winkelberechnungen
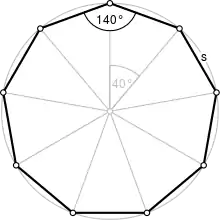
Der Winkel, den zwei benachbarte Seitenkanten im ebenen, regelmäßigen Neuneck miteinander einschließen, beträgt nach einer allgemeinen Formel für regelmäßige Polygone, in der für die Variable n die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall: n = 9):
Der spitze Winkel eines der neun Teildreiecke beträgt 360°/ 9 = 40°. Die Summe der Winkel beträgt 140° · 9 = 1260°.
Formel für die Fläche A
Ein Neuneck besitzt einen eindeutig bestimmbaren Flächeninhalt, welcher sich stets durch Zerlegen in Dreiecke berechnen lässt. Die Fläche des regelmäßigen Neunecks beträgt das Neunfache der Fläche eines jener Dreiecke, die von seinem Mittelpunkt und je zwei benachbarten Eckpunkten aufgespannt werden.
oder mit dem Umkreisradius:
Formel für die Seitenlänge a
Diagonalen
Es gibt drei Typen von Diagonalen, die zwei, drei bzw. vier Seiten einschließen. Ihre Längen betragen:
Die Differenz zwischen den Längen der längsten und der kürzesten Diagonalen ist gleich der Seitenlänge .
Näherungskonstruktionen
Nur mit Zirkel und Lineal (Euklidische Werkzeuge) kann ein regelmäßiges Neuneck nicht konstruiert werden.[1] Es gibt jedoch einige für die Praxis ausreichend genaue, mit euklidischen Werkzeugen mögliche Näherungskonstruktionen.
Dürer-Konstruktion
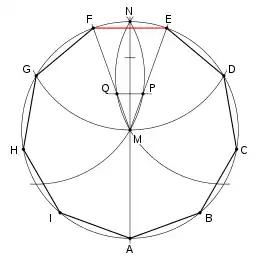
Eine elegante, aber auch ungenaue Näherungskonstruktion hat bereits Albrecht Dürer (1471–1528) verwendet:
- Auf dem Umkreis des Neunecks mit Mittelpunkt M und Radius r markiert man den Eckpunkt A.
- Dann schlägt man einen Kreis mit demselben Radius r um den gegenüberliegenden Kreispunkt N und erhält die beiden Eckpunkte D und G. (Anmerkung: Diese beiden Eckpunkte sind exakt, da die Diagonalen des Neunecks zwischen A, D und G ein gleichseitiges Dreieck ergeben.)
- Nun schlägt man wiederum mit dem Radius r zwei Kreise um die Punkte D und G.
- Als Nächstes wird die Strecke MN in drei Teile geteilt. Durch den Teilungspunkt, der näher beim Mittelpunkt des Neunecks liegt, wird ein Lot auf die Gerade MN gezeichnet.
- Die Schnittpunkte dieses Lotes mit den Kreislinien um D und G ergeben die Punkte P und Q.
- Schließlich verlängert man die Geraden MP und MQ, bis sie den Umkreis schneiden. Diese Schnittpunkte sind eine gute Näherung für die Eckpunkte E und F. Die Strecke EF ist eine gute Näherung für die Seitenlänge des Neunecks.
- Die Eckpunkte B, C, H und I erhält man durch Abschlagen der so gewonnenen Seitenlänge auf der Kreislinie.
Berechnung
Stellt man sich für die Dürer-Konstruktion ein Koordinatensystem mit M als Nullpunkt vor, so ergeben sich zunächst folgende Koordinaten:
Gesucht wird jetzt Punkt Q. Der Kreis um D durch M und N wird durch die Gleichung
beschrieben. Die Koordinaten von Schnittpunkt Q mit der Geraden erfüllt also beide Gleichungen. Durch Einsetzen der Geraden- in die Kreisgleichung erhält man:
- oder
Die Lösungen dieser Gleichung ergibt die X-Koordinaten der beiden Schnittpunkte des Kreises mit der Geraden, von denen die mit zum Punkt Q gehört (der andere liegt außerhalb der Darstellung).
- b.z.w.
Diese hat die Lösungen
Mit also
Damit gilt für Punkt Q
Der Mittelpunktswinkel ergibt sich damit zu
Hieraus ergibt sich eine um ca. 0,974 % kürzere Strecke als der wahre Wert der Seitenlänge. Bei einem Radius von 150 mm ist die Seite 1 mm zu kurz.
Zweite Konstruktion
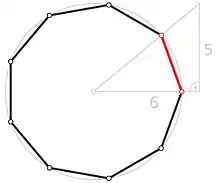
(Zweite Konstruktion)
Bei der einfachsten Näherungskonstruktion wird ein rechtwinkliges Dreieck mit den Katheten 6 und 5 verwendet.
Mit diesem Dreieck erhält man einen Winkel von ca. 39,80557°. Der relative Fehler F ist:
Bei einem Umkreisradius von ca. 313,5 mm ist die Seite 1 mm zu kurz.
Dritte Konstruktion
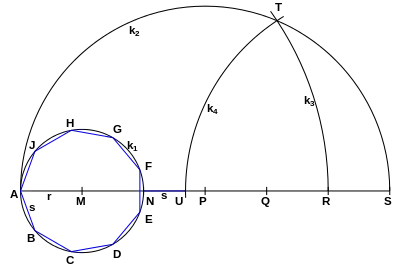
Eine wesentlich praktikablere Konstruktion wird wie folgt durchgeführt:
- Zeichne um einen Punkt M den Umkreis des Neunecks (k1).
- Zeichne einen Durchmesser AN und verlängere die Strecke auf das Dreifache.
- Trage auf dieser Geraden vier weitere Radien ab. Von Punkt A also insgesamt 6 Radien bis Punkt S.
- Zeichne über AS einen Thaleskreis (k2)
- Trage mit einem Bogen (k3) um Punkt A einen Abstand von 5 Radien am Thaleskreis ab (Punkt T).
- Trage mit einem Bogen (k4) um Punkt S den Abstand TS auf der Geraden ab (Punkt U).
- Die NU = s ist eine gute Näherung für die Seite des Neunecks.
Die Strecke s hat eine Länge von
Bei dieser Konstruktion beträgt der relative Fehler also
- %
Das entspricht bei einem Radius von 150,3 cm einer Abweichung von −1 mm. Die Seite ist also etwas zu kurz.
Exakte Konstruktionen
Erweitert man die Werkzeuge so, dass eine allgemeine Dreiteilung des Winkels möglich wird, z. B. um einen sogen. Tomahawk oder mit der Methode des Archimedes, so kann man durch Dreiteilung des mit Zirkel und Lineal konstruierbaren Winkels von 120° den benötigten Winkel von 40° erhalten.
Bei gegebenem Umkreis

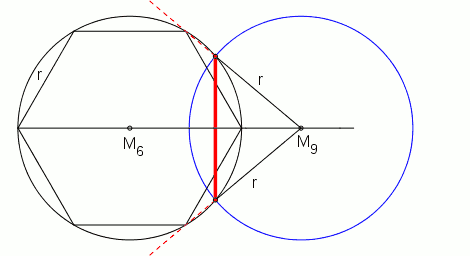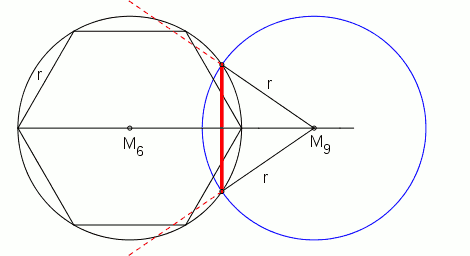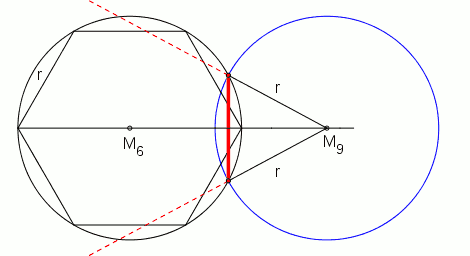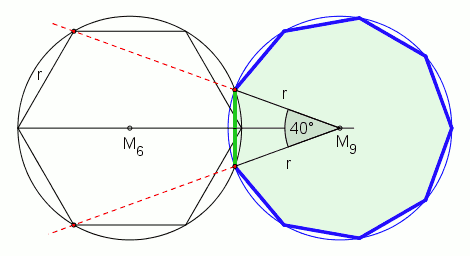
Bei gegebener Seitenlänge
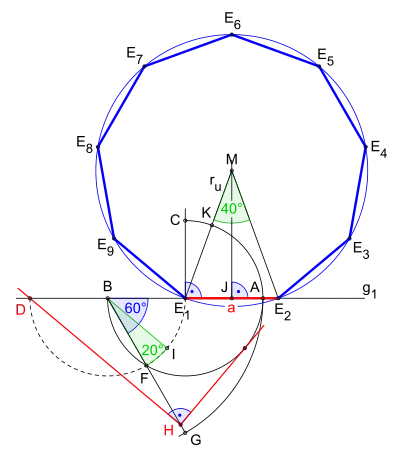
Ist die Seitenlänge eines regelmäßigen Neunecks gegeben, kann für die erforderliche Dreiteilung der Winkelweite z. B. die Methode Rechtwinkelhaken[3] nach Ludwig Bieberbach genutzt werden.
Im Folgenden sind die Schritte der nebenstehenden Konstruktion beschrieben.
- Trage auf der Geraden g1 die gegebene Seitenlänge a ab und bezeichne deren Enden mit E1 bzw. E2.
- Errichte eine Senkrechte auf g1 in E1
- Wähle nach eigenem Belieben den Punkt A auf g1 für den folgenden Dreiviertelkreis um E1 mit Radius r = E1A; ergibt die Schnittpunkte B und C.
- Ziehe einen Halbkreis um B mit dem Radius r; ergibt die Schnittpunkte D und F.
- Ziehe den Kreisbogen um B ab A.
- Zeichne eine Linie ab B durch F, bis sie den Kreisbogen in G schneidet. Dabei ergibt sich der Winkel GBA mit Winkelweite 60°.
- Um nun die Winkelweite 60° zu Dritteln lege z. B. ein Geodreieck folgendermaßen auf die Zeichnung:
- Der Scheitel vom Winkel 90° des Dreiecks bestimmt auf dem Winkelschenkel BG den Punkt H, eine Kathete des Dreiecks verläuft durch den Punkt D und die andere tangiert den Dreiviertelkreis um E1. Nach dem Verbinden des Punktes D mit H und dem Einzeichnen der Tangente ab H auf den Dreiviertelkreis um E1, zeigt sich der oben genannte Rechtwinkelhaken.
- Zeichne ab B eine Parallele zu DH, bis sie den Halbkreis um B in I schneidet. Der Winkel FBI ist mit seinen 20° der gedrittelte Teil des Winkels GBA.
- Halbiere a in J und errichte in J eine Senkrechte.
- Übertrage die Sehne FI auf den Dreiviertelkreis ab C mit Schnittpunkt K.
- Ziehe eine Linie ab E1 durch K, bis sie die Senkrechte auf a in M schneidet; somit ist der Umkreisradius ru = ME1 gefunden.
- Verbinde M mit E2; damit ergibt sich der Mittelpunktswinkel E1ME2 = μ = 40° des entstehenden Neunecks.
- Ziehe den Umkreis um M mit ru = ME1.
- Trage die Seitenlänge a siebenmal gegen den Uhrzeigersinn auf den Umkreis ab und verbinde die Eckpunkte zu einem regelmäßigen Neuneck.
Regelmäßige überschlagene Neunecke
Ein regelmäßiges überschlagenes Neuneck ergibt sich, wenn beim Verbinden der neun Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen , wobei die Anzahl der Eckpunkte angibt und jeder -te Punkt verbunden wird.
Es gibt nur zwei regelmäßige Neunstrahlsterne, auch Enneagramme genannt.
Die „Sterne“ mit den Symbolen {9/3} und {9/6} sind gleichseitige Dreiecke.
- Regelmäßige Neunstrahlsterne


Verwendung des Neunecks in der Praxis
Die Festungsstadt Palmanova ist auf einem Neuneck aufgebaut. Die jährlich erscheinenden 5-Euro-Silbermünzen aus Österreich haben die Form eines Neunecks.[4] Außerdem basiert die Architektur der Häuser der Andacht (die Sakralbauten der Bahai) auf einem Neuneck. Sternmotoren wurden meistens 5-, 7- oder 9-zylindrig gebaut. Der Grundriss der Hauptform der Befreiungshalle in Kelheim ist ein Achtzehneck, das wegen der Nichtkonstruierbarkeit des Neunecks ebenfalls nicht konstruierbar ist.
Weblinks
Einzelnachweise
- Emil Artin: Galoissche Theorie. Verlag Harri Deutsch, Zürich 1973, ISBN 3-87144-167-8, S. 85.
- Ernst Bindel, Helmut von Kügelgen: KLASSISCHE PROBLEME DES GRIECHISCHEN ALTERTUMS IM MATHEMATIKUNTERRICHT DER OBERSTUFE. (PDF) In: ERZIEHUNGSKUNST. Bund der Freien Waldorfschulen Deutschlands, August 1965, S. 234–237, abgerufen am 14. Juli 2019.
- Ludwig Bieberbach: Zur Lehre von den kubischen Konstruktionen, Journal für die reine und angewandte Mathematik. H. Hasse und L. Schlesinger, Band 167, Walter de Gruyter, Berlin 1932, S. 142–146, DigiZeitschriften, Bild auf S. 144 abgerufen am 8. August 2020.
- Oesterreichische Nationalbank: Münzbroschüre Ausgabe 2006 (Memento vom 5. März 2007 im Internet Archive) (pdf, 1,0 MB)