Almagest
Almagest (altgriechisch μαθηματική σύνταξις mathematiké sýntaxis, arabisch المجسطي, DMG al-maǧisṭī) nennt man eines der Hauptwerke der antiken Astronomie, das auf den Gelehrten Claudius Ptolemäus zurückgeht. Das Werk wurde im 2. Jahrhundert n. Chr. in Alexandria (heute Ägypten) geschrieben, das damals zum römischen Kaiserreich unter Hadrian gehörte. Üblicherweise wird der Sternkatalog auf das Jahr 137 n. Chr. datiert,[1][2][3] wobei die Teile (Bücher) des Gesamtwerks verschiedenen Alters sein könnten. Der Titel lautete griechisch Mathematike Syntaxis („Mathematische Zusammenstellung“; von μαθηματικός „zum Lernen gehörig, wissbegierig“), da im römischen Reich weiterhin Altgriechisch die lingua franca der Wissenschaft war.
Dieses Buch gilt als umfassendste und kompetenteste Darstellung des astronomischen Systems der griechisch-römischen Antike. Es ist ein Kompendium, also Zusammenstellung verschiedener Komponenten von Wissen in einem umfassenden Werk, das (wie der Titel sagt) Lehrbuch und für spätere Forschende auch Handbuch sein sollte. Es wurde während des gesamten kommenden Millenniums oft kopiert. Spätere Abschriften des hoch angesehenen Werkes trugen den Titel Megiste Syntaxis („Größte Zusammenstellung“), was als al-madschisti in die arabischen Übersetzungen übernommen wurde und von dort als Almagest in die lateinischen Übersetzungen und den heutigen Sprachgebrauch überging.[4] Im Gegensatz zu anderen Werken jener Zeit ist der Text des Almagest vollständig überliefert.
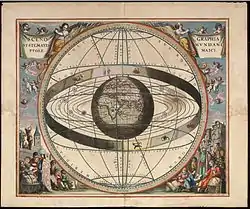
Der Almagest beruht auf dem geozentrischen ptolemäischen Weltbild und arbeitet dessen astronomische Details aus. Im Gegensatz zum eher physikalisch geprägten Werk Hypotheseis ton planomenon („Hypothesen über die Planeten“) des Ptolemäus steht im Almagest die mathematische Beschreibung der Bahnen der einzelnen Himmelskörper im Vordergrund. Wegen seiner exakten mathematischen Modellierung der Himmelsbewegungen und der dadurch eröffneten Möglichkeit, diese recht genau vorauszuberechnen, entwickelte er sich zum Standardwerk der mathematischen Astronomie vom 2. bis zum 17. Jahrhundert.
Aufgrund der thematisch sehr umfassenden und systematisch gegliederten Darstellung, verdrängte der Almagest schon sehr früh alle anderen griechischen astronomischen Schriften. Ptolemäus systematisierte darin das gesamte antike Wissen über die Himmelsobjekte, nutzte dabei das hohe Niveau der griechischen Mathematik und bettete sein System in die aristotelische Physik ein. Heute gilt das Werk als Höhepunkt und Abschluss der antiken Astronomie.
Neben dem Werk selbst sind auch antike Kommentare dazu überliefert, insbesondere von Pappos und Theon von Alexandria.
Inhalt
Die Standardedition ist die von Johan Ludvig Heiberg (1899),[5] auf dieser Edition basieren die deutsche Übersetzung von Manitius (1912, 1913)[1] in zwei Büchern und die englische Übersetzung von Gerald J. Toomer (1984), wobei letzterer auch Korrekturen aus der mittelalterlichen arabischen Handschriftenüberlieferung berücksichtigt.[2]
Der Inhalt und Aufbau des Almagest wurde für mehr als 1500 Jahre für alle astronomischen Handbücher das Vorbild. Wie Euklids Elemente besteht auch der Almagest aus 13 Büchern:
- Buch 1–2: Einführung in das ptolemäische Weltsystem und die mathematischen Hilfssätze
- Buch 3: Theorie der Sonne
- Buch 4–5: Theorie des Mondes
- Buch 6: Mond- und Sonnenfinsternisse
- Buch 7–8: Sterne und Sternkatalog (Verzeichnis der Sternbilder)
- Buch 9–13: Theorie der Planeten (Saturn, Jupiter, Mars, Venus und Merkur)
Weltbild
Als „Vorbesprechung“ stellt Ptolemäus einige Grundsätze auf:
- Das Himmelsgebäude hat Kugelgestalt und dreht sich wie eine Kugel.
- Ihrer Gestalt nach ist die Erde, als Ganzes betrachtet, gleichfalls kugelförmig.
- Ihrer Lage nach nimmt sie als Zentrum die Mitte des ganzen Himmels ein.
- Ihrer Größe und Entfernung nach ist sie im Verhältnis zur Fixsternsphäre wie ein Punkt.
- Die Erde vollzieht ihrerseits keinerlei Ortsveränderungen verursachende Bewegungen.
Die einfachen Vorstellungen von Kugeln und Kreisen standen jedoch nicht im Einklang mit den Beobachtungsdaten. Zwei Schwierigkeiten waren auffällig:
- die 1. Ungleichheit – Planeten durchlaufen die Bahnstücke mit ungleichmäßiger Geschwindigkeit,
- die 2. Ungleichheit – Planeten bewegen sich teilweise in die entgegengesetzte Richtung, ihre Bewegungen ähneln einer Art Schleife.
Zur Erklärung dieser Phänomene gab es verschiedene Modelle. Ptolemäus übernahm in seinem Werk die Epizykeltheorie des Apollonios von Perge mit ihren Epizykeln und Deferenten, da diese Theorie im Vergleich zum älteren Kugelschalen-Modell des Eudoxos von Knidos den Vorteil hatte, dass man es erweitern konnte (Epizykeln höherer Ordnung). Von Hipparch von Nicäa hingegen stammt die Idee der exzentrischen Lage des Deferenten (Exzentertheorie). Wegen der ungleichmäßigen Geschwindigkeit benötigte Ptolemäus zusätzlich auch noch einen Ausgleichspunkt, den so genannten Äquanten: von diesem Punkt aus erschien die Bewegung des Planeten dann wiederum gleichmäßig.
Die Sonnentheorie des Hipparch übernahm Ptolemäus unverändert, war jedoch der Meinung, dass dessen Mondtheorie wegen der komplexeren Mondbewegung genauer darzustellen sei. Dank der sehr genauen, durch eben jenen Hipparch überlieferten Daten der Mondbewegungen, ermittelte Ptolemäus in seiner Mondtheorie Werte, die durch Tycho Brahe spürbar verbessert werden konnten.
Der Almagest enthält unter anderem auch eine systematische Zusammenfassung der Kunst, aus der Messung von Winkeln und Strecken Entfernungen zu messen (Triangulation). Daraus entwickelte sich später die Trigonometrie (Dreiecksmessung). In Buch 1 findet man die berühmte Sehnentafel, einen Vorläufer unserer trigonometrischen Tafeln, von ½° bis 180° in ½°-Schritten (dies entspricht im Wesentlichen der Sinustafel von ¼° bis 90° in ¼°-Schritten). Es folgen weitere Sätze der ebenen und sphärischen Trigonometrie.
Auch enthält der Almagest einen Katalog der Himmelsobjekte. Dieses Inventar besteht aus den Angaben zu 1025 Sternen in 48 Sternbildern. Dieser Katalog galt die nächsten 15 Jahrhunderte dann auch als stilbildend für den Aufbau, die Fachausdrücke und die Koordinatenangaben aller seiner Nachfolger.
Fixsternsphäre (Sternkatalog)
Der Sternkatalog des Almagest beschreibt die für den antiken Beobachter unveränderliche Sphäre der fest angeordneten Punkte am Nachthimmel. Die Bücher 7 und 8 des Almagest widmen sich folgenden Themen:
- Feststellung, dass die Lage der Sterne relativ zueinander unveränderlich ist (d. h. die Sterne des Großen Wagens z. B. verschieben sich nicht gegeneinander).
- Feststellung, dass es aber eine systematische Verschiebung der Sternbilder entlang der Ekliptik gibt, d. h. die Koordinaten der Sterne ändern sich systematisch (Präzession) in zwei Schritten. Daraus leitet sich die Notwendigkeit des ekliptikalen Koordinatensystems ab, da der Almagest für die nächste Jahrhunderte gedacht ist und es dem künftigen Leser möglichst einfach gemacht werden soll, die gegebenen Koordinaten in seine eigene Zeit zu transformieren. Die zwei Schritte sind:
- Die Jahreshauptpunkte (z. B. Frühlingspunkt) wandern durch den Tierkreis, liegen also etwa alle 2000 Jahren in einem anderen Sternzeichen.
- Die Sternbilder des Tierkreises verschieben sich nicht gegenüber den Sternbildern außerhalb des Tierkreises.
- Ermittlung des Betrags dieser Verschiebung (Präzessionskonstante) anhand von historischen Sternbedeckungen durch den Mond
- Sternkatalog, geordnet nach Sternbildern, diese geordnet nach "nördlich der Ekliptik", "an der Ekliptik", "südlich der Ekliptik"
- Anleitung zum Bau eines Globus mit den zuvorgenannten Sternkoordinaten. Der Globus fungiert als eine Art analoger Computer zur Berechnung der Phänomene (z. B. heliakischer und mathematischer Auf- und Untergänge, Kulminationen etc.)
- Beschreibung des Verlaufs der Milchstraße für den Globus.

Aufbau des Sternkatalogs
Der Sternkatalog ist als Tabelle angeordnet. Nicht nur die griechischen Handschriften (Kopien) und lateinischen Übersetzungen machen das so.[6] Ptolemäus schreibt expressis verbis, dass die Koordinaten als (ekliptikale) „Längen“ und „Breiten“ angegeben sind, die in Spalten angegeben sind, so dass dies wohl auch schon immer so gewesen ist. Bezeichnend ist, dass Ptolemäus sich aufgrund seiner Kenntnis der Präzession für das ekliptikale Koordinatensystem entscheidet, was ihn von allen seinen Vorgängern unterscheidet. Hipparchs Himmelsglobus hatte zwar eine eingezeichnete Ekliptik, aber die Koordinaten waren äquatorial.[7] Da der Sternkatalog von Hipparch nicht im Original überliefert ist, sondern im Almagest-Sternkatalog aufging (und in der Zeit von 265 Jahren dazwischen stark überarbeitet wurde),[7][8] ist der Almagest-Sternkatalog der älteste, bei dem uns komplette Tupel von Koordinaten und Helligkeitsangaben überliefert sind.
Der Tierkreis hat in der griechischen Antike (seit seiner Einführung, spätestens bei Eudoxos) nicht in erster Linie eine astrologische Funktion, sondern eine metrische: Individualhoroskope gibt es seit augusteischer Zeit, während der Tierkreis in der griechischen mathematischen Astronomie Jahrhunderte früher eingeführt wurde. Bereits Hipparch unterschied sauber zwischen "Sternbildern" (Figuren aus Sternen) und Sternzeichen (den zwölf Abschnitten des Tierkreises).[7] Die Sternzeichen, d. h. die zwölf Abschnitte à 30° des Vollkreises der Ekliptik, dienen im ekliptikalen Koordinatensystem zur Bezeichnung der Position. Beginnend bei Aries (Widder), werden 30° Aries gezählt, dann 30° Taurus, dann 30° Gemini usw. Der Punkt, den wir heute 98° ekliptikale Länge nennen würden, hieß also bei allen griechischen Astronomen 8° Cancer.

Auch im Almagest stimmen Sternbilder und Sternzeichen nicht überein: Die Sternzeichen sind alle gleich lang (30° auf der Ekliptik), während die Sternbilder alle unterschiedlich groß sind, einander teilweise überlappen und teilweise Lücken lassen.
Sternbilder im Almagest
Der Sternkatalog enthält 48 Sternbilder, die unterschiedliche Flächenausdehnung und Sternanzahl besitzen. In Buch VIII, Kapitel 3 schreibt Ptolemäus zwar, dass die Sternbilder auf einem Globus umrissen werden sollen, es ist aber unklar, wie er das genau meint: Sollen umgebende Polygone gezeichnet werden oder die Figuren skizziert werden oder gar Strichfiguren gezeichnet werden? Das wird nicht gesagt.
Obwohl keine Strichfiguren aus der Antike überliefert sind, kann man anhand der Beschreibungen im Sternkatalog die Figuren rekonstruieren: Es ist ja genau verzeichnet, an welcher Himmelskoordinate Kopf, Füße, Arme, Flügel und sonstige Körperteile der Figuren liegen.[7] Es ist daher möglich, die Strichfiguren im modernen Sinn so zu zeichnen, dass sie zur Beschreibung im Almagest passen. Diese modernen Strichfiguren als Rekonstruktion der historischen Sternbilder des Almagest sind seit 2019 in der freien Planetariumssoftware Stellarium verfügbar.
Diese Sternbilder bilden die Grundlage für die modernen Sternbilder, die 1930 international festgelegt wurden.
Fehler in den Sternkoordinaten
Tycho Brahe entdeckte, dass die Sternkoordinaten im Almagest einen systematischen Fehler aufweisen. Alle sind um ca. 1° verschoben längs der Ekliptik verschoben,[3] worüber sich zahlreiche Astronomen seither den Kopf zerbrachen (u. a. Tycho Brahe selbst, Laplace, Lalande im 18. Jh., Delambre im 19. Jh., Björnbo, H. Vogt, Dreyer in the beginning of the 20th century)[3].

Festgestellt wurde, dass die Koordinaten tatsächlich nicht zur Epoche/ Äquinoktium des Almagest (137 n. Chr.) passen, sondern etwa ein Jahrhundert früher, in die Mitte des ersten Jahrhunderts datieren.[7][3] Als Erklärungsversuche wurde angeboten:
- dass alle Koordinaten aus hipparchschen Beobachtungen berechnet sind, wobei die damals zu ungenau bekannte Präzessionskonstante zu einem Summenfehler führte (Delambre 1817)[3]
- dass die Daten in Wahrheit ein Jahrhundert früher von Menelaos von Alexandria beobachtet worden seien (Björnbo 1901)[3]
- dass die Differenz eine Summe aus Einzelfehlern verschiedener Fehler ist, u. a. Kalibration mit veralteten Sonnendaten (Dreyer 1917[9])[3]
- dass das Instrument von Ptolemäus falsch kalibriert war und einen systematischen Offset hatte (Vogt 1925)[10]
Zieht man den systematischen Fehler ab, bleiben weitere Fehler übrig, die nicht mit der Präzession erklärt werden können. Von diesen Fehlern finden sich ca. 18 bis 20 auch im (nur unvollständig rekonstruierbaren) Sternverzeichnis von Hipparch.[3][7] Daraus lässt sich schließen, dass eine Untermenge von Sternkoordinaten des Almagest tatsächlich auf Hipparch zurückgeht,[3] nicht aber, dass der komplette Sternkatalog einfach "nur" abgeschrieben sei. Vielmehr sind die größten Fehler Hipparchs im Almagest nicht mehr vorhanden[7] und andererseits hatte Hipparchs Sternverzeichnis einige Sterne, die im Almagest gänzlich fehlen.[7] Daraus lässt sich schließen, dass Hipparchs Sternkatalog zwar die Grundlage bildet, aber nachbeobachtet und überarbeitet worden ist.[7][8]
Problematik
Mit dem epizyklischen Modell ließen sich zwar die Planetenbewegungen im Rahmen damaliger Messgenauigkeit sehr zuverlässig vorausberechnen, allerdings um den Preis von Widersprüchen zu den Grundlagen der aristotelischen Physik: die Bewegung der Planeten erfolgte nicht mehr um den Weltmittelpunkt (wegen exzentrischer Lage des Deferenten) und die Gleichförmigkeit der Planetenbewegungen war nur durch mathematische Tricks zu gewährleisten. Deshalb sprach man schon sehr früh von der Rettung der Phänomene. Damit war gemeint, dass die Astronomie eher als Zweig der Geometrie denn als Zweig der Physik zu sehen sei. Sie sei lediglich für die genaue mathematische Darstellung der Gestirnsbewegungen zuständig.
Eine fundamentale Kritik am Almagest – nämlich dass die angegebenen Beobachtungsdaten aus Berechnungen entstanden und als Beobachtungsdaten somit gefälscht waren – übte in den 1970er Jahren der amerikanische Astrophysiker Robert Russell Newton. Sein Buch mit dem reißerischen Titel "The Crime of Ptolemy" machte zwar den Amerikaner populär – aber die Idee, dass die Koordinaten im Almagest-Sternkatalog älter sein könnten als der Almagest, kursiert seit ca. vierhundert Jahren (seit Tycho Brahe feststellte, dass sie einen systematischen Fehler haben) und an zahlreichen Stellen im Buch wird auf frühere Astronomen Bezug genommen. Die Behauptung eines wissenschaftlichen Vergehens ("crime") von Ptolemäus ist also unberechtigt,[3][7] zumal der Almagest als Kompendium selbstverständlich älteres Wissen kompiliert: Es werden darin sowohl babylonische Beobachtungen zitiert als auch ältere griechische (z. B. von Timocharis, Aristyll, Hipparch, Agrippa, Menelaos von Alexandria). Der Rückgriff auf ältere wissenschaftliche Daten ist bis heute eine Methode der Wissenschaft.[11][12]
Überlieferung
Die ältesten erhaltenen griechischen Manuskripte des Almagest sind der Pariser Codex 2389 in der Nationalbibliothek (möglicherweise ursprünglich aus der Laurentiana in Florenz und von Katharina von Medici nach Frankreich gebracht) und der Codex Vaticanus Graecus 1594, beide aus dem 9. Jahrhundert.[13] Der Vatican-Codex ist das schönste erhaltene Exemplar und wurde von Heiberg für seine Ausgabe zugrundegelegt. Es gibt auch Codices aus dem 10. Jahrhundert (Codex Venedig 313) und 11. Jahrhundert (Laurentiana, Pluteus 89,48). Peters und Knobel zählen 1915 insgesamt 21 Griechische, 8 Lateinische und 25 Arabische Codices auf (ihre Liste ist aber unvollständig). Unter den arabischen Manuskripten ragt British Museum, Reg. 16, A. VIII heraus (15./16. Jahrhundert, von Nasīr ad-Dīn at-Tūsī, ehemals im Besitz des türkischen Sultans). Die früheste erhaltene arabische Übersetzung (Bagdad 827) von al-Haddschadsch ibn Yusuf ibn Matar und des Byzantiners Elias ist in einem Codex in Leiden (Codex Leidensis 399) erhalten.
Im 9. Jahrhundert wurden viele griechische Schriften bei den Arabern bekannt, unter anderem der Almagest. Dieser wurde jetzt auch mehrfach übersetzt und kommentiert. So entwickelte er sich zur Grundlage des astronomischen Beobachtens und Rechnens im arabischen Raum. Eine frühe Übersetzung (Ende 8. Jahrhundert) ins Syrische und die erste arabische Übersetzung sind verschollen. Die früheste erhaltene arabische Version stammt von al-Haddschadsch ibn Yusuf ibn Matar. Die beste Übersetzung (aus der Zeit um 879 bis 890) verdanken wir Ishaq ibn Hunayn, dem Sohn des Meisterübersetzers Hunain ibn Ishāq; sie wurde von Thabit ibn Qurra überarbeitet.[14][15] Handschriften der beiden Ausgaben sind bis heute erhalten und gelangten im Mittelalter auch ins muslimische Spanien.
Da man während des Frühmittelalters im westlichen Europa kaum Zugang zu griechischen Quellen der Antike hatte, war hier auch der Almagest unbekannt. Obwohl Astronomie Teil des Quadriviums war, waren die Kenntnisse auf diesem Gebiet doch eher gering. Das änderte sich jedoch mit dem steigenden Interesse an der Astrologie, denn dafür waren genaue Daten der Astronomie gefragt. In der zweiten Hälfte des 12. Jahrhunderts wurden dann endlich mehrere Astronomiewerke zugänglich, darunter neben dem von Thabit ibn Qurra und Abu Maʿschar al-Balchi (Albumasar) auch der Almagest. Dieser wurde aus dem Arabischen durch Gerhard von Cremona ins Lateinische übersetzt und war die überwiegend im lateinischen Mittelalter verwendete Ausgabe. Gerhard arbeitete zunächst mit der Haddschadsch-Version, im Verlauf der Arbeit bekam er die Hunain-Thabit-Übersetzung in die Hände, worauf er nicht nur die Vorlage wechselte, sondern auch die bereits übersetzten Kapitel anhand dieser exakteren Version überarbeitete. Gerhards Übersetzung ist, wie alle seine Übersetzungen, extrem wörtlich.[16]
Ab Mitte des 13. Jahrhunderts bekam der Almagest in den astronomischen Vorlesungen der Universitäten starke Konkurrenz durch die Theorica planetarum („Planetentheorie“), eine anonyme Abhandlung, die wahrscheinlich durch einen Lehrer der Pariser Universität verfasst wurde.[17] Die Planetentheorie beschrieb die ptolemäische Grundtheorie für jeden Planeten und ergänzte diese Beschreibung durch weitere Zeichnungen.
Im Jahr 1451 erstellte der griechische Gelehrte Georg von Trapezunt aus griechischen Quellen eine Übersetzung ins Lateinische (gedruckt in Venedig 1528 bei Giunti), die jedoch als unzulänglich kritisiert wurde, u. a. von Kardinal Bessarion. Es gab auch schon eine Übersetzung direkt aus dem Griechischen durch einen anonymen Übersetzer im 12. Jahrhundert in Sizilien,[18] die aber kaum Verbreitung fand (vier Handschriften von ihr oder Teilen von ihr sind erhalten). Außerdem ist eine unvollständige Handschrift einer Übersetzung vom Arabischen ins Lateinische aus dem frühen 12. Jahrhundert im Kreuzfahrerstaat Antiochia bekannt.[19] Die Astronomen Georg von Peuerbach und dann Regiomontanus arbeiteten an besseren Übersetzungen, starben jedoch früh. Eine Zusammenfassung von Regiomontan, der „Epitom“, wurde erst zwanzig Jahre nach seinem Tod gedruckt, 1496 als „Epytoma Ioa[n]nis de Mo[n]te Regio in Almagestu[m] Ptolomei“. Dieses Bessarion gewidmete Werk war für zwei Jahrzehnte eine der wichtigsten Grundlagen der Astronomie, auch Copernicus gehörte zu den Besitzern eines Exemplars. In einer vollständigen Lateinischen Fassung erschien der Almagest erst 1515 in Venedig (bei Petrus Lichtenstein in der Übersetzung aus dem Arabischen von Gerhard von Cremona). Der Druck der ersten griechischen Originalfassung folgte 1538 in Basel (bei Joh. Walder), die Simon Grynaeus und Joachim Camerarius der Ältere nach einer ehemals im Besitz von Regiomontanus befindlichen und später verlorenen Handschrift anfertigten.[20] In Basel erschienen 1543 auch die lateinischen Werke von Regiomontanus und Peuerbach über das Almagest, „Ioannis de Monte Regio et Georgii Purbachii Epitome in Cl. Ptolomaei magnam compositionem …“. Im selben Jahr erschien in Nürnberg das Werk „De Revolutionibus“ des Nicolaus Copernicus, das in der Form an den Almagest anknüpfte, und dazu führte, dass das im Almagest dargestellte geozentrische Weltbild durch das kopernikanische heliozentrische abgelöst wurde. Die größten Verfechter des neuen Weltbildes wurden über ein halbes Jahrhundert später Galileo Galilei und Johannes Kepler. Die Keplerschen Gesetze leiteten dann auch die Entwicklung der modernen Astronomie ein. Erasmus Reinhold etwa veröffentlichte 1549 den Almagest als Griechisch-Lateinische Gegenüberstellung, und 1551 seine Prutenischen Tafeln mit Daten von Copernicus.
Da bei der mittelalterlichen arabischen und lateinischen Überlieferung des Almagest und anderer Schriften von Ptolemäus großer Forschungsbedarf besteht, wurde dies Gegenstands eines Projekts der Bayerischen Akademie der Wissenschaften (Ptolemaeus Arabus et Latinus).[21]
Ausgaben und Übersetzungen
- Johan Ludvig Heiberg: Claudii Ptolemaei opera quae exstant omnia. Teubner, Leipzig,
- 1. Syntaxis Mathematics. 1898 (griechische Textausgabe);
- 2. Opera astronomica minora. 1903 (griechische Textausgabe).
- Nachdruck Teubner, Leipzig 1963, 2 Bände (Übersetzung von Manitius mit Korrekturen von Otto Neugebauer)
- Karl Heinrich August Manitius: Des Claudius Ptolemäus Handbuch der Astronomie. Teubner, Leipzig,
- 1. 1912 (deutsche Übersetzung), archive.org;
- 2. 1913 (deutsche Übersetzung), archive.org.
(auf Heiberg fußende Übersetzung ins Deutsche)
- Englische Übersetzung von Robert Catesby Taliaferro in der Reihe Great Books of the Western World (Encyclopedia Britannica) 1955
- Gerald J. Toomer (Hrsg.): Ptolemy’s Almagest. Translated and Annoted. Duckworth, London 1984; Neudruck Universität Princeton, Princeton 1998, ISBN 0-691-00260-6 (Englische Übersetzung).
Literatur
- Christian H. F. Peters, Edward Ball Knobel: Ptolemy’s Catalogue of Stars. A Revision of the Almagest. Washington 1915 (= Carnegie Institution of Washington. Band 86).
- Gerd Grasshoff: The History of Ptolemy’s Star Catalogue. Springer, New York 1990, ISBN 3-540-97181-5 (Analyse des im „Almagest“ überlieferten Sternenkatalogs).
- Paul Kunitzsch: Der Almagest. Die Syntax mathematica des Claudius Ptolemäus in arabisch-lateinischer Überlieferung. Harrassowitz, Wiesbaden 1974, ISBN 3-447-01517-9 (zugleich München, Universitäts, Habilitationsschrift).
- Paul Kunitzsch (Herausgeber, Übersetzer): Der Sternkatalog des Almagest. Die arabisch-mittelalterliche Tradition. I. Die arabischen Übersetzungen. Harrassowitz, Wiesbaden 1986.
- Olaf Pedersen: A Survey of the Almagest. Odense University Press, Odense 1974 (= Acta historica scientiarum naturalium et medicinalium. Band 30). (Detaillierte Erläuterungen zur Astronomie des Almagest). Neuauflage von Alexander Jones, Springer 2011.
- Otto Neugebauer: A History of Ancient Mathematical Astronomy. Springer: Berlin/ Heidelberg/ New York 1975.
Weblinks
- Der Sternkatalog im Almagest (Memento vom 15. November 2007 im Internet Archive)
- Ausgabe 1496 an der “Digital Rare Book Collection” at the Vienna University Observatory univie.ac.at
- Ausgabe 1515 als Digitalisate bei der Bayerischen Staatsbibliothek und an der Uni Wien (PDF).
- Ausgabe 1543 als Digitalisat bei Bayerischen Staatsbibliothek
- Übersetzung „Des Claudius Ptolemäus Handbuch der Astronomie / Karl Manitius“ als Digitalisat im Internet Archive: Buch I-VI Buch VII-XIII
- „Syntaxis Mathematics / Griechische Textausgabe von Johan Ludvig Heiberg“ als Digitalisat im Internet Archive: Buch I-VI Buch VII-XIII
- Diverse Digitalisate bei Wilbour Hall at Brown University – former home to the History of Mathematics Department
- Paul Kunitzsch: Ptolemäus und die Astronomie: Der Almagest, Akademie Aktuell, Bayerische Akademie der Wissenschaften, 2013, Heft 3, S. 18–23, mit anderen Aufsätzen zu Ptolemäus hier: Akademie Aktuell 2013, Nr.3
- Ptolemaeus Arabus et Latinus: Almagest
Einzelnachweise
- Manitius: Handbuch der Astronomie. Warburg Institute, abgerufen am 18. November 2021.
- Toomer and Ptolemy: Ptolemy's Almagest. Princeton, New Jersey 1998, ISBN 978-0-691-21336-1.
- Gerd Grasshoff: The History of Ptolemy's Star Catalogue. Springer New York, New York, NY 1990, ISBN 978-1-4612-4468-4.
- Paul Kunitzsch: Der Almagest. Die Syntaxis mathematica des Claudius Ptolemäus in arabisch-lateinischer Überlieferung. Wiesbaden 1974, S. 115 f.
- Heiberg: Syntaxis Mathematika. Abgerufen am 18. November 2021.
- Ptolemaios: Mathematike Syntaxis. In: Bayerische Staatsbibliothek, Münchener Digitalisierungszentrum. 1345, abgerufen am 18. November 2021 (gr).
- Susanne M. Hoffmann: Hipparchs Himmelsglobus : ein Bindeglied in der babylonisch-griechischen Astrometrie? Wiesbaden 2017, ISBN 978-3-658-18683-8.
- Hoffmann, Susanne M: The genesis of Hipparchus' celestial globe. In: Mediterranean Archaeology and Archaeometry. Band 18. Athens, S. 281–287.
- Dreyer: On the origin of Ptolemy's catalogue of stars. 1917, abgerufen am 18. November 2021.
- H. Vogt: Versuch einer Wiederherstellung vonHipparchs Fixsternverzeichnis. In: Astronomische Nachrichten. Band 224, Nr. 2-3, 1925, S. 17–54, doi:10.1002/asna.19252240202 (wiley.com [abgerufen am 18. November 2021]).
- Steele, John M.: Applied historical astronomy: an historical perspective. In: Journal for the History of Astronomy. Band 35, Nr. 3, 2004, S. 337 - 355.
- Gudrun Wolfschmidt, Susanne M Hoffmann: Applied and Computational Historical Astronomy. Angewandte und computergestützte historische Astronomie. - Proceedings of the Splinter Meeting in the Astronomische Gesellschaft, Sept. 25, 2020. In: Nuncius Hamburgensis - Beiträge zur Geschichte der Naturwissenschaften. 1. Auflage. Band 55. tredition, Hamburg 2021, ISBN 978-3-347-27104-3.
- Christian Peters, Edward Knobel, Ptolemy's Catalogue of Stars, A revision of the Almagest, Carnegie Institution, Washington D.C. 1915, S. 18ff (Liste der Manuskripte des Almagest).
- Kunitzsch, Der Almagest 1974, S. 59 ff.
- Kunitzsch, Ptolemäus und die Astronomie: der Almagest, Akademie Aktuell 03/2013, Bayr. Akad. Wiss., S. 18ff
- Kunitzsch, Der Almagest 1974, S. 34 und 85f.
- Olaf Pedersen: The origins of the Theorica Planetarum. In: Journal of the History of Astronomy, Band 12, 1981, S. 113, bibcode:1981JHA....12..113P
- Walter Berschin: Griechisch-Lateinisches Mittelalter. Von Hieronymus zu Nikolaus von Kues. Francke 1980, englischer Auszug. Dazu C. H. Haskins Studies in the history of medieval science, Cambridge/Massachusetts 1924
- Kunitzsch, Akademie Aktuell 03/2013, S. 23
- Olaf Pedersen: A survey of the Almagest. Springer 2011, S. 21
- Dag Nikolaus Hasse, Benno von Dalen, David Juste: Ptolemaeus Arabus et Latinus, Einführung, Akademie aktuell 03-2013, Bayerische Akademie der Wissenschaften, S. 9ff