Arabische Zahlschrift
Sogenannte arabische Ziffern sind die zehn Ziffern: 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9. Der Begriff impliziert oft eine Dezimalzahl, die mit diesen Ziffern geschrieben wird (insbesondere im Gegensatz zu römischen Ziffern). Die europäischen Zeichen für diese Ziffern haben nicht die Form, die in der arabischen Welt heute verwendet wird, sondern eine, die historisch daraus entstanden ist.

2021 |
| 2021 in heute weltweit verbreiteter Druckschrift |
٢٠٢١ |
| 2021 in arabisch-indischer Druckschrift |
२०२१ |
| 2021 in der Devanagari-Schrift |
௨௦௨௧ |
| 2021 in tamilischer Schrift |
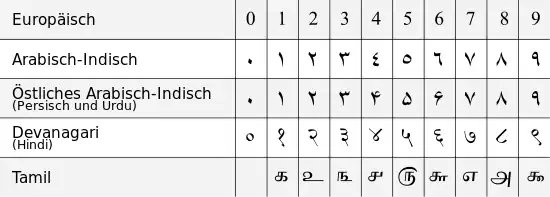
Die arabischen Ziffern, auch indische oder indisch-arabische Ziffern genannt, sind die elementaren Zeichen einer Zahlschrift, in der Zahlen auf der Grundlage eines Dezimalsystems mit neun aus der altindischen Brahmi-Schrift herzuleitenden Zahlzeichen positionell dargestellt werden. Die Null als zehntes Zeichen wird oft durch ein als Kreis oder Punkt geschriebenes Zahlzeichen dargestellt. Diese Zahlschrift hat sich in der Neuzeit weltweit durchgesetzt.
Entstehung und Ausbreitung


Indien
Am Beginn der Entwicklung der indischen Ziffern stand die Brahmi-Zahlschrift. Sie ist zusammen mit der Brahmi-Schrift ab dem 3. Jahrhundert v. Chr. im altindischen Maurya-Reich belegbar.
शून्य (śūnya) – null
Unter dem Wort śūnya (n., Sanskrit शून्य, „die Leere, das Nichts, das Nichtvorhandensein“) wurde die Zahl Null geboren. Die philosophische Grundlage dafür war wahrscheinlich das buddhistische Konzept śūnyatā (f., Sanskrit शून्यता, „die Leerheit, die illusorische Natur der Phänomene“) wie es Nāgārjuna (2. Jahrhundert n. Chr.) in der Lehre von der Leerheit (śūnyatāvāda) beschrieben hat.[1] Als weitere Bezugsquelle kommt die Schreibung des Wertes Null als Leerzeichen durch die Babylonier ab dem 6. Jahrhundert v. Chr. in Betracht.[2] Als Lückenzeichen im dezimalen Stellenwertsystem taucht die Null, dargestellt durch einen Punkt, im Bakhshali-Manuskript auf, das in einer kontrovers diskutierten Radiokarbonuntersuchung in seinen ältesten Teilen ins 3. bis 4. Jahrhundert n. Chr. datiert wurde.[3]
Brahmasphutasiddhanta
Im Jahr 628 n. Chr. verfasste der indische Astronom und Mathematiker Brahmagupta das Brahmasphutasiddhanta („Der Anfang des Universums“). Es ist, wenn man vom Zahlensystem der Maya absieht, der früheste bekannte Text, in dem die Null als vollwertige Zahl behandelt wird. Darüber hinaus stellte Brahmagupta in diesem Werk Regeln für die Arithmetik mit negativen Zahlen und mit der Zahl 0 auf, die weitgehend unserem modernen Verständnis entsprechen. Der größte Unterschied bestand darin, dass Brahmagupta auch die Division durch 0 zuließ, während in der modernen Mathematik Quotienten mit dem Divisor 0 nicht definiert sind.
Weiterentwicklung
Die weltweite Verbreitung der indischen Ziffern ging nicht direkt mit einer weltweiten Verbreitung des Brahmasphutasiddhanta einher, sondern benötigte einige Zwischenschritte.
Arabische Verbreitung
Zwischen 640 und 644 eroberten die Araber den Irak und Persien. Die ersten überlieferten Hinweise auf indische Zahlzeichen im Westen stammen von dem syrischen nestorianischen Bischof Severus Sebokht im 7. Jahrhundert.
Al-Chwarizmi
Um 825 schrieb der persische Mathematiker, Astronom und Geograph al-Chwarizmi sein Werk über das Rechnen mit indischen Zahlzeichen, das nur in lateinischer Übersetzung bekannt ist (Algoritmi de numero indorum, 12. Jahrhundert).[4]
Die Null wird bei den Arabern als ṣifr (arabisch الصفر, DMG aṣ-ṣifr ‚null, nichts‘) vom Verb ṣafira („leer sein“) bezeichnet – eine Lehnübersetzung des Wortes śūnya. Daraus entstand das Wort Ziffer.
Der Sprung ins Abendland
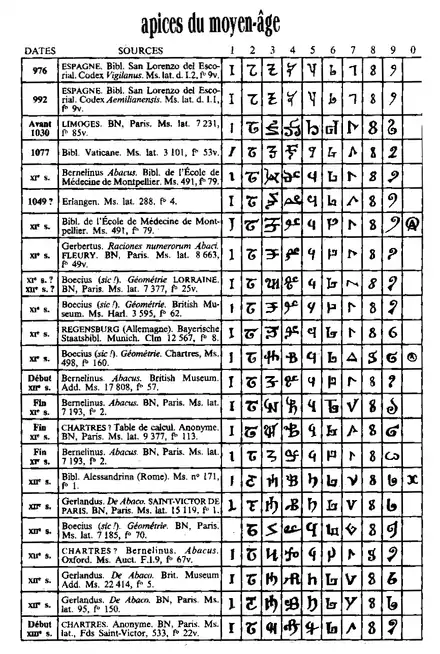
Die arabischen Ziffern sind „die heute gebräuchlichen Ziffern, d. h. die von den Arabern übernommenen, ursprünglich indischen zehn Zahlzeichen. Sie entstanden im 10. Jahrhundert in Katalonien aus den westarabischen Gobar- oder Staubziffern und wurden von dem Mönch Gerbert (dem späteren Papst Silvester II.) auf den Rechensteinen (Apices) ins Abendland eingeführt (damals noch ohne das Zeichen für die Null). […] Im Geschäftsleben setzten sie sich wegen der Fälschungsgefahr nur langsam gegen die römischen Ziffern durch, in Deutschland erst im 15. Jahrhundert.“[5]
Liber abaci
Der Italiener Leonardo Fibonacci folgte um 1192 seinem Vater nach Algerien und lernte dort Abū Kāmils Algebra kennen. 1202 vollendete Fibonacci den Liber abaci, in welchem er unter anderem die indischen Ziffern vorstellte und diese in der Tat als „indische Ziffern“ und nicht als „arabische Ziffern“ bezeichnete. Von Italien aus fanden diese Ziffern dann auch Eingang in weitere europäische Länder.
Weltweite Verbreitung
In der Folge verdrängten die arabischen Ziffern in Europa die sperrigeren römischen. Zwar konnten auch mit den römischen einfache Berechnungen durchgeführt werden. Jedoch erst die arabischen ermöglichten höhere Mathematik. Inzwischen werden sie weltweit verwendet.
Michael Schmidt-Salomon begründet diesen Erfolg evolutionär-humanistisch. Die Bevorzugung dieser Ziffern sei nicht die Folge von Kulturimperialismus, sondern der „besonderen Fruchtbarkeit der arabischen Zahlen“ geschuldet.[6]
Typographische Varianten
Dieser Abschnitt ist der historischen Entstehung der verschiedenen typographischen Varianten und den heute gebräuchlichen Formen der indischen Ziffern gewidmet.
Indische Varianten
Da in Indien bereits vor einigen tausend Jahren astronomische Beobachtungen systematisch und auf einem hohen Niveau betrieben worden sind, wurden große Zahlen benötigt – Lakh [lakʰ] und Crore [kror] (Hindi: लाख, lākh; करोड़, karoṛ). Ein Lakh entspricht 100.000, ein Crore sind 100 Lakh, entspricht also 10.000.000. Diese Zahlen haben sich auf dem indischen Subkontinent, obwohl sie offiziell gegen das Tausendersystem ausgetauscht wurden, gehalten und sind dort noch heute im allgemeinen Sprachgebrauch zu finden.
Arabische Varianten
In der arabischen Schrift entwickelte sich die Schreibweise von rechts nach links aus einer ursprünglich senkrechten Beschriftung der Papyri von oben nach unten (sie waren aus Längsstreifen zusammengeklebt), das dann aber zum Lesen um 90 Grad gedreht wurde.[7] Ebenso wurden die indischen Zahlzeichen notiert, die deshalb in der Schrift gegenüber dem indischen Original teilweise eine gedrehte Form erhielten und dann weiter dem graphischen Stil der arabischen Schrift angepasst wurden. Der Aufbau der arabischen Worte der indischen Zahlzeichen geht ähnlich wie in westlichen Sprachen vom höchsten Stellenwert (also der linken Ziffer) aus. Beispielsweise setzte sich das Wort für 10.000 (ʕashrat ʔalāf) aus dem Wort ʔashara für 10 und ʔalf für 1000 zusammen. Ähnlich wie in westlichen Sprachen gibt es aber auch Sonderregeln wie bei den Zehnern – beispielsweise ist der Name für 19 tisʕata-ʕschar aus tisʕa für 9 und ʕaschara für 10 wie auch bei der Neunzehn im Deutschen. Geschrieben werden Zahlen in Ziffernform von links nach rechts (im Gegensatz zu den Buchstaben, die im Arabischen von rechts nach links geschrieben werden). Die Stellung der Ziffern ist wie sonst üblich im Dezimalsystem (also die Ziffern mit dem höchsten Stellenwert links).
Bevor die Araber das indische Stellenwertsystem übernahmen, benutzten sie für die Darstellung von Zahlen die Buchstaben ihres Alphabets, denen wie bei vielen anderen Schriftsystemen wie dem altgriechischen, römischen oder hebräischen neben dem Lautwert jeweils auch ein Zahlenwert zugewiesen war (vgl. arabisches Alphabet). Diese Möglichkeit wird auch heute teilweise noch in bestimmten Situationen angewendet, vergleichbar mit der Nutzung römischer Zahlen im westlichen Sprachraum.
Im Maghreb, das heißt, in den arabischsprachigen Ländern westlich des Niltals, verwendet man traditionell Zahlzeichen, die mit den europäischen identisch sind und nicht die hier als arabisch vorgestellten Zeichen.
Europäische Varianten

In Europa lassen sich vor allem zwei Darstellungsformen von Ziffern unterscheiden: Versalziffern und Mediävalziffern.
Die meistverbreitete Variante sind Versalziffern: Alle Ziffern haben die gleiche Höhe, und zwar die der Großbuchstaben (Versalien). Um einen sauberen Tabellensatz zu ermöglichen, sind Versalziffern meistens alle gleich breit, nämlich so breit wie ein Halbgeviert. Diese Variante wird auch als Tabellenziffern bezeichnet. Weniger gebräuchlich sind versale Proportionalziffern, bei denen insbesondere die 1 schmaler als die anderen Ziffern ist. Der Nachteil der Versalziffern ist, dass sie im Lauftext einen optischen Fremdkörper bilden und dass bei einigen Halbgeviert-breiten Ziffern (etwa bei der 1) auch der Abstand zu den benachbarten Ziffern oder Buchstaben zu groß wirkt.
Aus diesem Grund verfügen gut ausgebaute Schriften über einen zweiten Satz Ziffern, die Mediävalziffern. Diese haben wie Kleinbuchstaben Ober- und Unterlängen und in der Regel eine individuelle, der Zeichenform angepasste Laufweite. Damit fügen sie sich nahtlos und nach typografischen Gesichtspunkten korrekt in den Text ein. Manche Schriften bieten auch Mediävalziffern gleicher Breite für den Tabellensatz an.
Literatur
- Paul Kunitzsch: Zur Geschichte der ‘arabischen’ Ziffern. Bayerische Akademie der Wissenschaften, Phil.-hist. Klasse, Sitzungsberichte, 2005:3. Beck, München 2005 (Digitalisat).
Quellen
- Die Logik der Lehre von der Leere: Die Shunyata des Nagarjuna (Memento vom 30. Juli 2003 im Webarchiv archive.today)
- Robert Kaplan: Die Geschichte der Null. Campus-Verlag, Frankfurt am Main u. a. 2000, ISBN 3-593-36427-1.
- Sarah Gibbens: Altes Manuskript liefert neue Hinweise auf den Ursprung der Zahl Null. National Geographic, 9. November 2017.
- The Arabic numeral system. McTutor Archiv
- arabische Ziffern. Universal-Lexikon (Memento vom 27. März 2019 im Internet Archive)
- Michael Schmidt-Salomon: Hoffnung Mensch. Eine bessere Welt ist möglich. Piper Verlag, München 2014, S. 200.
- Georges Ifrah: Universalgeschichte der Zahlen (englische Ausgabe). Wiley, 2000, S. 533.