Gnomon
Der Gnomon (von griechisch γνώμων Gnomon Schattenzeiger) ist ein bereits vor der Antike bekanntes astronomisches Instrument in der Form eines senkrecht in den Boden gesteckten hölzernen Stabes. Vom Holzstab als Schattenzeiger aus ging die Entwicklung bis zur gelegentlichen einschlägigen Verwendung eines Obelisken. Der Sonnenschatten seiner Spitze wird beobachtet, um astronomische Größen zu bestimmen.

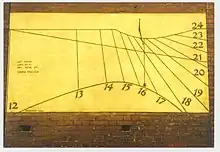
Er diente u. a. als Schattenstab für Sonnenuhren.[1] In Anlehnung an diese frühe Verwendung heißt die Lehre von der Sonnenuhren Gnomonik, und die Zentralprojektion einer Kugelfläche (z. B. der Himmelskugel, in der sich die Sonne befindet) durch ihren Mittelpunkt (dargestellt z. B. durch eine Gnomonspitze) wird als Gnomonische Projektion bezeichnet.
Anwendung
In der Antike wurde der Gnomon zur Bestimmung der geografischen Breite eines Ortes, der Nordrichtung, der Tagundnachtgleichen (Äquinoktien), der Sonnenwenden (Solstitien) und der Ekliptik verwendet. Dazu wurde der Gnomon in der Regel als einfacher Stab (meistens aus Holz), selten als Obelisk oder als besonderes Bauwerk ausgeführt. Allen Gnomonen gemeinsam ist die besondere Ausführung der Spitze: Damit deren Schatten scharf abgebildet wird und damit präzise ablesbar ist, ist sie spitz geformt oder mit einer kleinen Kugel (Nodus) versehen. Eine Variante mit durchlochter Scheibe an der Spitze zum Erzeugen eines Lichtflecks ist bereits aus dem Alten China bekannt.[2]
Nach dem Gnomon ist eine Zentralprojektion der Himmelskugel auf eine Ebene benannt, die gnomonische Projektion. Mit ihr kann der Schattenpunkt des Nodus für jeden Standort und Sonnenstand berechnet und auf dem Zifferblatt ein zweidimensionales Kurvennetz konstruiert werden. Auf den Linien, die alle Kegelschnitte sind, lässt sich sowohl die Tages- als auch die Jahreszeit ablesen.
Geschichte
Am Anfang wurde vermutlich vom Gnomon, der der Mensch selbst sein konnte, nur die Schattenlänge abgelesen und interpretiert. Ein astronomisches Instrument mit Gnomon könnte ein Mittagsweiser gewesen sein. Damit wurde mit Hilfe einer auf dem Boden in Meridian-Richtung angebrachten Skala die Mittagsschattenlänge gemessen.
Über diesen sehr frühen Schritt in verschiedenen Kulturen (einschließlich altes China) ist nur wenig bekannt. Auf einer babylonischen Tontafel aus der Zeit um 2300 v. Chr. sind die Schattenlängen eines Gnomons zu verschiedenen Zeiten angegeben.
Bei den Chinesen soll der Gnomon seit frühesten Zeiten ein wichtiges astronomisches Instrument gewesen sein. In einem der ältesten Mathematikbücher, dem Zhoubi suanjing, stellt der im elften Jahrhundert v. Chr. lebende Herzog von Zhou, Zhou Gong Dan, seinem Hofbeamten Shang Gao mathematische Aufgaben, darunter auch die Umrechnung der Schattenlänge des Gnomons in den Sonnenstand. Chinesische Astronomen haben den Gnomon mindestens bis zur frühen Yuan-Dynastie verwandt und weiterentwickelt (siehe Gaocheng-Observatorium). Laut Herodot (ca. 485–425 v. Chr.) haben die Griechen das Prinzip des Gnomons von den Babyloniern übernommen.
Durch Ausrüstung eines Mittagsweisers mit einer Stundenskala entstand schließlich eine vollwertige Sonnenuhr. Texte zu und Funde von Sonnenuhren gibt es aus dem alten Ägypten. Die altägyptische Schattenuhr und eine gleichzeitig verwendete Wandsonnenuhr waren aber nicht geeignet, die Tagesstunden zu jeder Jahreszeit richtig anzuzeigen. Beide Uhren verwendeten einen horizontalen Schattenwerfer, eine Kante die eine, einen Stab die andere. Dieser Sonnenuhrentyp wurde im Mittelalter erneut benutzt (siehe kanoniale Sonnenuhr). Von Sonnenuhren ab dem vierten Jahrhundert v. Chr. in Griechenland berichtet Vitruv (siehe Hauptartikel Sonnenuhr).
Eratosthenes von Kyrene stellte 225 v. Chr. Messungen mit Gnomonen an, aus denen er den Erdumfang zu etwa 252.000 Stadien berechnete. Er stellte fest, dass sich die Mittagshöhe der Sonne in Alexandria von der in Syene (Assuan) um etwa 7,2° unterscheidet. Mit diesem Winkel und der bekannten Distanz von etwa 5.000 Stadien zwischen den beiden, ungefähr auf dem gleichen Längengrad liegenden Städten erhielt er ein Ergebnis, das dem tatsächlichen Wert von 40.024 Kilometern (etwa 240.000 Stadien) sehr nahekommt.
Mathematische Grundlagen zur Nutzung des Gnomons
Projektion der Sonne auf ein Zifferblatt
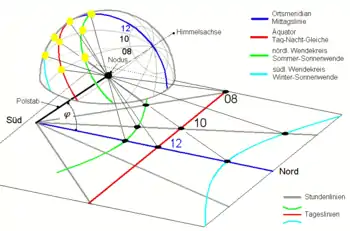
Die Abbildung der Sonne durch einen Punkt ist eine Zentralprojektion. Sie wird wegen ihrer Entwicklung im Zusammenhang mit der Gnomonik auch Gnomonische Projektion genannt. Das Projektionszentrum liegt im Zentrum des Himmels (gleich Zentrum der Erde). Die Vereinfachung, das Projektionszentrum auf die Erdoberfläche in die Spitze eines Gnomons zu verlegen, ist für die Aufgabenstellung zulässig, da die Sonne so weit entfernt ist, dass die Parallaxe aufgrund des Erdradius vernachlässigbar ist.
Abbildung [3] zeigt eine Gnomonische Projektion mit lotrechtem Gnomon und horizontaler Projektionsfläche, die z. B. die Fläche des Zifferblattes einer Sonnenuhr ist (horizontale Sonnenuhr). Alle Großkreise wie der Himmelsäquator und der durch den Standort verlaufende Meridian werden bei der Gnomonischen Projektion als Geraden abgebildet. Da die Stundenkreise der Sonne ebenfalls Großkreise sind, werden sie auf dem Zifferblatt als ein Geradenbüschel (Stundengeraden) abgebildet, das im Durchstoßpunkt der Polachse auf der Projektionsfläche konvergiert. Die Wendekreise werden als Hyperbeln abgebildet. Damit ist ersichtlich, dass der Schatten der Gnomonspitze zur Tagundnachtgleiche (Äquinoktium) von Sonnenaufgang bis -untergang auf einer Geraden verläuft und dabei die Stundengeraden schneidet. Zur Sonnenwende bewegt er sich auf einer Hyperbel und schneidet dabei über den Tagesverlauf ebenfalls die Stundenlinien.
Abbildung [3] zeigt, dass der Schatten des lotrechten Gnomonstabes die Stundengeraden schneidet. Würde der Stab im Durchstoßpunkt der Polachse auf die Projektionsfläche gestellt und in Richtung Himmelspol zeigen, so würde sein Schatten ebenso wie die Stundengeraden vom Durchstoßpunkt aus radial nach außen verlaufen. Somit würde jeder Punkt des Schattens die Zeit richtig zeigen. Ein solcher Stab heißt Polstab. Er bildet die Sonne eindimensional ab.
Messungen mit dem Gnomon
Nordrichtung
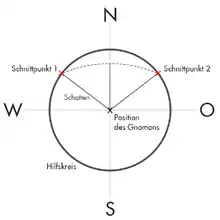
Um die Nordrichtung bestimmen zu können, ist es zunächst notwendig, den Zeitpunkt zu finden, zu dem die Sonne ihren Höchststand erreicht. Hierzu nutzt man aus, dass ihr Lauf am Himmel symmetrisch um diesen Punkt verläuft. Auf der horizontalen Oberfläche, zu welcher der Gnomon senkrecht steht, wird ein Kreis eingezeichnet, dessen Mittelpunkt der Schattenstab selbst bildet. Der Radius wird dabei so gewählt, dass er der Schattenlänge zum ersten Messzeitpunkt am Vormittag entspricht. Im Verlauf des Tages stimmt die Schattenlänge am Nachmittag noch genau ein weiteres Mal exakt mit dem Radius überein, wie in Abbildung [4] erkenntlich. Verbindet man die beiden Schnittpunkte mit dem Mittelpunkt und zeichnet die Winkelhalbierende der entstehenden Scheitel ein, so lässt sich feststellen, dass sie die Richtung des Schattens beim Sonnenhöchststand markiert.
- Da nördlich des nördlichen Wendekreises die Sonne zu ihrem Höchststand im Süden steht, kennzeichnet die Winkelhalbierende, die ihr exakt gegenüberliegt, die Nordrichtung.
- Südlich des südlichen Wendekreises hingegen handelt es sich bei der Winkelhalbierenden um die Südrichtung, da die Sonne von dort aus gesehen im Norden steht.
- Befindet man sich zwischen den beiden Wendekreisen, so hängt es von der Jahreszeit ab, ob der Schatten zur Mittagszeit nach Norden oder nach Süden fällt.
Sonneneinfallswinkel
Ist die Höhe des Gnomons sowie die Länge des von diesem auf die horizontale Oberfläche geworfenen Schattens bekannt, so lässt sich der Höhenwinkel der Sonne mithilfe von Trigonometrie bestimmen:
Dies ist möglich, da der Gnomon zusammen mit der Oberfläche, zu welcher er im Lot steht, sowie einem einfallenden Sonnenstrahl, der die Hypotenuse darstellt, ein rechtwinkliges Dreieck bildet.
Begriffsverwendung in der Geometrie
In der Mathematik, speziell in der planaren Geometrie, bezeichnet der Begriff Gnomon die Restfläche zwischen zwei ähnlichen Figuren. Diese Konstruktion war schon in der griechisch-hellenistischen Mathematik bekannt und bezeichnete eine geometrische Figur, die entsteht, wenn man aus einem Parallelogramm ein ihm ähnliches und ähnlich gelegenes so ausschneidet, dass es eine Ecke mit dem ursprünglichen Parallelogramm gemeinsam hat.
Bisweilen werden auch die jeweils zwei flächengleichen Ergänzungsparallelogramme einer solchen Konstruktion als Gnomon bezeichnet. Sie entstehen, wenn durch einen Punkt der Diagonale Geraden gezogen werden, die parallel zu den Seiten des Parallelogramms sind (siehe Satz vom Gnomon).[3]
Gnomon-Metapher in der Literatur zur Bibelexegese
In theologischer Fachliteratur fand der Begriff Gnomon in einem berühmten Werk der Bibelexegese eine Verwendung in übertragenem Sinn als Metapher.
Im Jahr 1742 veröffentlichte der pietistische Theologe Johann Albrecht Bengel (1687–1752) den lateinischen Gnomon Novi Testamenti, einen um Genauigkeit bemühten Kommentar zum Neuen Testament, der den wahren Sinn des Textes aufschließen, aufzeigen sollte. Mit dieser emblematisch (sinnbildlich)[4] ausgerichteten Wahl des Begriffs "Zeiger" weist Bengel auf sein Interesse an der seiner Ansicht nach chronologisch fassbaren, berechenbaren Heilsgeschichte hin, die, entsprechend den seiner Ansicht nach durch ihn entschlüsselten Aussagen der Johannes-Apokalypse wie ein Uhrwerk ablaufen sollte. Bengels Schwiegersohn Philipp David Burk verwandte den Begriff ebenfalls in seiner Exegese der Psalmen.
Literatur
- Oskar Becker: Das mathematische Denken der Antike. 2. Auflage. Mit einem Nachtrag von Günther Patzig. Vandenhoeck & Ruprecht, Göttingen 1966, ISBN 3-525-25304-4 (Studienhefte zur Altertumswissenschaft 3).
- François Dom Bedos di Celles: La Gnomonique pratique, ou l'art de tracer les cadrans solaires. Avec des observations sur la maniere de regler les Hozloges. Chez Briasson, Despilly, Hardy, Paris 1760. Faksimile-Ausgabe: Laget, Librairie Paris 1978, ISBN 2-85204-076-X.
- Dieter Lelgemann, Eberhard Knobloch, Andreas Fuls, Andreas Kleineberg: Zum antiken astro-geodätischen Messinstrument Skiotherikós Gnomon. In: ZfV. Zeitschrift für Geodäsie, Geoinformation und Landmanagement. 130, Heft 4, 2005, ISSN 1618-8950, S. 238–247.
- Helmut Minow: Schattenmessung mit dem Gnomon. In: ZfV. Zeitschrift für Geodäsie, Geoinformation und Landmanagement. 130, Heft 4, 2005, S. 248–252.
- René R. J. Rohr: Die Sonnenuhr. Geschichte, Theorie, Funktion. Callwey, München 1982, ISBN 3-7667-0610-1.
- Karlheinz Schaldach, Römische Sonnenuhren. Eine Einführung in die antike Gnomonik. 3. Auflage. Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1649-7.
- Karl Schoy: Über den Gnomonschatten und die Schattentafeln der arabischen Astronomie. Ein Beitrag zur arabischen Trigonometrie nach unedierten arabischen Handschriften. Lafaire, Hannover 1923.
- Vitruvius: Vitruvii De architectura libri decem. = Zehn Bücher über die Architektur. Übersetzt und mit Anmerkungen versehen von Curt Fensterbusch. Lizenzausgabe. 5. Auflage. Primus, Darmstadt 1996, ISBN 3-89678-005-0.
Einzelnachweise
- René R. J. Rohr: Die Sonnenuhr. Geschichte, Theorie, Funktion. Callwey, München 1982, ISBN 3-7667-0610-1, S. 10.
- René R. J. Rohr: Die Sonnenuhr. Geschichte, Theorie, Funktion. Callwey, München 1982, ISBN 3-7667-0610-1, S. 13.
- Der neue Brockhaus 2. Band, p. 399, Wiesbaden 1959.
- Vgl. Reinhard Breymayer: "Gnomon typusque vitae Christianae". Zum emblematischen Hintergrund des "Gnomon"-Begriffs bei Heinrich Oraeus (1584–1646) und bei Johann Albrecht Bengel (1687–1752)". In: Blätter für württembergische Kirchengeschichte, Jg. 88 (1988). Festschrift für Gerhard Schäfer. Hrsg. von Martin Brecht. Stuttgart [1989], S. 289–323.