Minkowski-Diagramm

Das Minkowski-Diagramm wurde 1908 von Hermann Minkowski entwickelt und dient der Veranschaulichung der Eigenschaften von Raum und Zeit in der speziellen Relativitätstheorie. Es erlaubt ein quantitatives Verständnis der damit verbundenen Phänomene wie beispielsweise der Zeitdilatation und der Längenkontraktion ohne Formeln.

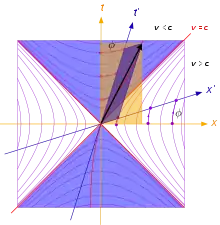
Minkowski-Diagramm mit dem Ruhesystem (x,t), dem bewegten System (x’,t’), mit Lichtkegel und Hyperbeln, die Raum und Zeit bezüglich des Koordinatenursprungs bestimmen

Das Minkowski-Diagramm ist ein Raum-Zeit-Diagramm mit nur einer Raum-Dimension. Dabei wird eine Überlagerung der Koordinatensysteme für zwei gegeneinander mit konstanter Geschwindigkeit bewegte Beobachter dargestellt, sodass zu den Orts- und Zeitkoordinaten x und t, die der eine Beobachter zur Beschreibung des Geschehens verwendet, unmittelbar die des anderen x’ und t’ abgelesen werden können und umgekehrt. Aus dieser grafisch eineindeutigen Zuordnung von x und t zu x’ und t’ wird unmittelbar die Widerspruchsfreiheit zahlreicher scheinbar paradoxer Aussagen der Relativitätstheorie ersichtlich. Auch die Unüberwindbarkeit der Lichtgeschwindigkeit erschließt sich grafisch als Folge der Eigenschaften von Raum und Zeit. Die Form des Diagramms folgt unmittelbar und ohne Formeln aus den Postulaten der speziellen Relativitätstheorie und verdeutlicht die enge Verwandtschaft von Raum und Zeit, die aus der Relativitätstheorie hervorgeht. Eine Erweiterung ist das Penrose-Diagramm, mit dem man die globale Struktur von allgemeineren, auch gekrümmten, Raumzeiten darstellen kann.

Grundlagen

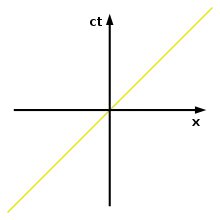
Mit ct anstelle von t auf der Zeitachse wird die Weltlinie eines Lichtteilchens zu einer Geraden mit einer Steigung von 45°.

Zugunsten der Darstellbarkeit wird bei den Minkowski-Diagrammen auf zwei der drei Raumdimensionen verzichtet und nur das Geschehen in einer eindimensionalen Welt betrachtet. Anders als bei Weg-Zeit-Diagrammen üblich, wird der Weg auf der x-Achse und die Zeit auf der y-Achse dargestellt. Damit lässt sich das Geschehen auf einem horizontalen Weg unmittelbar in das Diagramm hineindenken, wobei sich dieser Weg mit dem Verstreichen der Zeit von unten nach oben durch das Diagramm hindurch bewegt. Jedes Objekt auf diesem Weg, wie beispielsweise ein Beobachter oder ein Fahrzeug, beschreibt auf diese Weise eine Linie im Diagramm, die man seine Weltlinie nennt.

Jeder Punkt in diesem Diagramm markiert eine bestimmte Stelle in Raum und Zeit. Eine solche Stelle wird als Ereignis bezeichnet unabhängig davon, ob zu dieser Zeit und an diesem Ort überhaupt etwas geschieht.

Es erweist sich als vorteilhaft, auf der Zeitachse nicht die Zeit t direkt, sondern die zugeordnete Größe ct aufzutragen, wobei c = 299792,458 km/s die Lichtgeschwindigkeit bezeichnet. Einer Sekunde entspricht auf diese Weise ein Abschnitt von 299792,458 km auf der Ordinate. Wegen x = ct für ein Lichtteilchen, das den Koordinatenursprung nach rechts passiert, ist seine Weltlinie eine um 45° geneigte Gerade im Diagramm, sofern für beide Koordinaten-Achsen der gleiche Maßstab gewählt wird.

Weg-Zeit-Diagramm in der newtonschen Physik

In der newtonschen Physik wird das Ereignis bei A von beiden Beobachtern demselben Zeitpunkt zugeordnet.

Das nebenstehende Diagramm stellt das Koordinatensystem eines Beobachters dar, den wir der Einfachheit halber als den Ruhenden bezeichnen wollen, und der sich bei x = 0 befindet. Die Weltlinie des Beobachters ist daher mit der Zeitachse identisch. Jede Parallele zu dieser Achse entspräche einem ebenfalls ruhenden Objekt an einem anderen Ort. Die blaue Gerade entspricht dagegen einem Objekt, das sich mit konstanter Geschwindigkeit nach rechts bewegt, beispielsweise einem bewegten Beobachter.

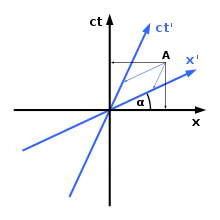
Diese blaue Gerade lässt sich nun als die Zeitachse dieses Beobachters interpretieren, die zusammen mit der für beide Beobachter identischen Raumachse sein Koordinatensystem darstellt. Das entspricht einer Vereinbarung der beiden Beobachter, die Stelle x = 0 und t = 0 auch mit x′ = 0 und t′ = 0 zu bezeichnen. Das Koordinatensystem des bewegten Beobachters ist schiefwinklig. Zum Ablesen der Koordinaten eines Punktes werden in diesem Fall die beiden Parallelen durch den Ereignispunkt zu den Achsen gebildet und ihr Schnittpunkt mit den Achsen betrachtet.

Es zeigt sich am Beispiel des Ereignisses A im Diagramm, dass damit für die Ortskoordinate wie erwartet verschiedene Werte ermittelt werden, da sich der bewegte Beobachter seit t = 0 auf den Ort des Ereignisses zubewegt hat. Andererseits findet in der newtonschen Physik ein Ereignis aus der Sicht beider Beobachter zum selben Zeitpunkt statt. Der Maßstab auf der Zeitachse des bewegten Beobachters ist daher gestreckt, derart dass in gleicher Höhe über der x-Achse auf beiden Zeitachsen dieselben Werte stehen.

Generell finden alle Ereignisse, die sich auf einer Parallelen zur Wegachse befinden, gleichzeitig statt und zwar für beide Beobachter. Es gibt nur eine universelle Zeit t = t′, was sich in der Existenz einer gemeinsamen Wegachse äußert. Analog steht die Existenz zweier verschiedener Zeitachsen in Zusammenhang damit, dass beide Beobachter verschiedene Ortskoordinaten ermitteln. Diese grafische Übersetzung der Koordinaten x und t in x′ und t′ beziehungsweise umgekehrt erfolgt mathematisch über die Galilei-Transformation.

Minkowski-Diagramm in der speziellen Relativitätstheorie

In der Relativitätstheorie wird das Ereignis bei A unterschiedlichen Zeitpunkten zugeordnet, ct_A > ct′_A.

Unterschiedliche Skalierung der Achsen.

Albert Einstein (1905) entdeckte nun, dass die newtonsche Beschreibung nicht der Realität entspricht.[1] Je höher die betrachteten Geschwindigkeiten sind, desto größer werden die Abweichungen. Raum und Zeit sind so beschaffen, dass für die Übersetzung der Koordinaten zwischen bewegten Beobachtern andere Regeln gelten. Insbesondere finden Ereignisse, die der eine Beobachter als gleichzeitig bewertet, für den anderen, relativ zu ihm bewegten Beobachter zu verschiedenen Zeiten statt. Diese Relativität der Gleichzeitigkeit wurde von Hermann Minkowski auf elegante Weise veranschaulicht.[2]

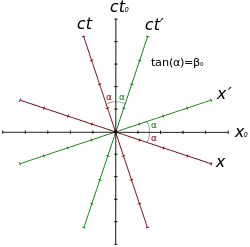
Im Minkowski-Diagramm entspricht die Relativität der Gleichzeitigkeit der Existenz verschiedener Wegachsen für die beiden Beobachter. Jeder Beobachter interpretiert nach obiger Regel alle Ereignisse auf einer Geraden parallel zu seiner Wegachse als gleichzeitig. Der Ablauf des Geschehens aus der Sicht eines bestimmten Beobachters lässt sich damit grafisch durch Parallelverschiebung einer solchen Geraden von unten nach oben nachvollziehen.

Bei Auftragung von ct anstelle t auf der Zeitachse erweist sich der Winkel α zwischen den beiden Wegachsen als identisch mit dem zwischen den beiden Zeitachsen. Als Ursache für diese Orientierung der Wegachsen lässt sich das Prinzip von der Konstanz der Lichtgeschwindigkeit interpretieren (siehe unten). Der Winkel α ergibt sich aus der Relativgeschwindigkeit v zu

\tan \alpha ={\frac {v}{c}}=\beta

.

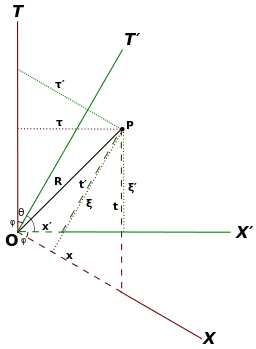
Die zugehörige Übersetzung der Koordinaten x und t in x′ und t′ beziehungsweise umgekehrt erfolgt mathematisch über die Lorentz-Transformation. Die Skalierung der Achsen ergibt sich folgendermaßen: Wenn U die gewählte grafische Länge der benutzten Längeneinheit (z. B. 1 Ls = 1 Lichtsekunde) auf den ct- und x-Achsen ist, markieren wir diese beiden Achsen wie gewohnt im grafischen Abstand U vom Ursprung mit einer 1 (in nebenstehender Grafik U). Der grafische Abstand U′ vom Ursprung, in dem die erste Markierung auf ct′- und x′-Achsen erfolgt, ergibt sich dann zu:[3]

U'=U\cdot {\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}

.

Erläuterung: Stellt die ct-Achse die Weltlinie einer in S ruhenden Uhr dar, dann entspricht U der mit c multiplizierten Dauer zwischen zwei auf dieser Weltlinie auftretenden Ereignissen, was als Eigenzeit der Uhr bezeichnet wird. Die Länge U auf der x-Achse entspricht der Ruhelänge oder Eigenlänge eines in S ruhenden Maßstabs. Dieselben Zusammenhänge gelten auch für die Abstände U′ auf der ct′- und x′-Achse. Die erste Markierung auf der ct′-Achse hat im System S′ die mathematischen Koordinaten (x′,ct′) = (0,1) und die erste Markierung auf der x′-Achse hat die mathematischen Koordinaten (x′,ct′) = (1,0). Im ungestrichenen Koordinatensystem S ergibt sich mit der Lorentz-Transformation, dass die erste Markierung auf der ct′-Achse die mathematischen Koordinaten (x,ct) = (γ v/c,γ) hat. Da das ungestrichene Koordinatensystem grafisch ein kartesisches Koordinatensystem ist, ergibt sich der grafische Abstand der Markierung dann nach dem Satz des Pythagoras und Vereinfachung zur oben angegebenen Formel:

U'=U\cdot {\sqrt {{\frac {\beta ^{2}}{1-\beta ^{2}}}+{\frac {1}{1-\beta ^{2}}}}}=U\cdot {\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}

Dasselbe Ergebnis erhält man auch bei Betrachtung der x′-Achse.

Symmetrisches Minkowski-Diagramm

Bild 1: Sicht im Mittelsystem

Bild 2: Symmetrisches Minkowski-Diagramm

Bild 3: Symmetrisches Minkowski-Diagramm gemäß Gruner und Sauter: Kovariante und kontravariante Komponenten

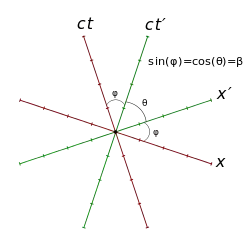
Sofern nur zwei Inertialsysteme betrachtet werden, kann die unterschiedliche Skalierung auf den Achsen vermieden und eine symmetrische Darstellung erreicht werden. Denn zwischen zwei relativ bewegten Inertialsystemen existiert immer ein drittes, in dem sich die beiden anderen mit gleicher Geschwindigkeit in entgegengesetzte Richtung bewegen („Mittelsystem“). Wenn $\beta =v/c$ und $\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}$ zwischen zwei Inertialsystemen $S$ und $S'$ gegeben sind, dann sind sie folgendermaßen mit den entsprechenden Größen im Mittelsystem $S_{0}$ verbunden:[4][5]

{\begin{aligned}(1)&&\beta &={\frac {2\beta _{0}}{1+\beta _{0}^{2}}}\\(2)&&\beta _{0}&={\frac {\gamma -1}{\beta \gamma }}\end{aligned}}

Wenn beispielsweise $\beta =0{,}5$ zwischen S und S’ gegeben ist, dann bewegen sie sich gemäß (2) in ihrem Mittelsystem $S_{0}$ mit annähernd ±0,268 c in jeweils entgegengesetzter Richtung. Oder wenn $\beta _{0}=0{,}5$ in $S_{0}$ gegeben ist, dann ist gemäß (1) die Relativgeschwindigkeit zwischen S und S′ in ihren eigenen Ruhesystemen gegeben mit 0,8 c. Die Konstruktion der entgegengesetzt gerichteten Achsen von S und S′ erfolgt dann nach der gewöhnlichen Methode mit $\tan \alpha =\beta _{0}$ in Bezug auf die orthogonalen Achsen des Mittelsystems (siehe Bild 1).

Es zeigt sich jedoch, dass die Konstruktion dieser symmetrischen Minkowski-Diagramme wesentlich vereinfacht werden kann, wobei weder das Mittelsystem $S_{0}$ noch $\beta _{0}$ aufgeführt werden müssen, sondern lediglich $\beta$ zwischen S und S′:[6] Wenn $\varphi$ der Winkel ist zwischen der ct′- und ct-Achse (und zwischen der x- und x′-Achse), und $\theta$ zwischen der x′- und ct′-Achse, dann ergibt sich:[7][8]

{\begin{aligned}\sin \varphi =\cos \theta &=\beta ,\\\cos \varphi =\sin \theta &=1/\gamma ,\\\tan \varphi =\cot \theta &=\beta \cdot \gamma .\end{aligned}}

Daraus ergeben sich beispielsweise die zwei folgenden Konstruktionsmethoden (Bild 2): Die x-Achse wird zuerst senkrecht zur ct′-Achse gezeichnet, dann werden die x′ und ct-Achsen im Winkel $\varphi$ beigefügt; oder die x′-Achse wird im Winkel $\theta$ bezüglich der ct′-Achse gezeichnet, dann die x-Achse senkrecht zur ct′-Achse und die ct-Achse senkrecht zur x′-Achse beigefügt. Zusätzlich (Bild 3) ergibt sich, dass die Parallelprojektionen von Vektor $R$ seinen kontravarianten Komponenten (x,t; x′,t′) entsprechen, und die Orthogonalprojektionen ${\displaystyle (\xi ,\tau$ seinen kovarianten Komponenten.

Geschichte

Max Born (1920) verwendete in seinem Buch Die Relativitätstheorie Einsteins verschiedene Minkowski-Diagramme mit zwei sich zueinander senkrecht ausbreitenden Lichtstrahlen als Achsenkreuz. Um die Symmetrie von Längenkontraktion und Zeitdilatation darzustellen, fügte er noch die Achsen zweier Systeme S und S′ hinzu, wobei die x-Achse annähernd senkrecht zur ct′-Achse, und die x′-Achse annähernd senkrecht zur ct-Achse stand.[9]
Dmitry Mirimanoff (1921) entdeckte die Existenz von „Mittelsystemen“, die immer bezüglich zweier relativ zueinander bewegter Inertialsysteme aufgefunden werden können. Er zeigte jedoch keine graphische Interpretation dieses Zusammenhangs.[4]
Paul Gruner (1921) entwickelte zusammen mit Josef Sauter symmetrische Diagramme auf systematische Weise. Es wurden relativistische Effekte wie Längenkontraktion und Zeitdilatation abgeleitet sowie der Zusammenhang von kontravarianten und kovarianten Komponenten.[7][8] Gruner erweiterte diese Methode in weiteren Arbeiten (1922–1924) und würdigte die Leistung Mirimanoffs.[10][11][12][13][14][15]
Die Konstruktion solch symmetrischer Diagramme wurde später mehrmals neu entdeckt. Beispielsweise veröffentlichte Enrique Loedel Palumbo beginnend mit 1948 mehrere Arbeiten in spanischer Sprache, worin er diese Methode entwickelte.[16][17] 1955 wurde sie abermals durch Henri Amar wiederentdeckt.[18][19] In einigen Lehrbüchern werden solche Diagramme daher als „Loedel-Diagramme“ bezeichnet.[20][6]

Zeitdilatation

Zeitdilatation: Beide Beobachter messen die Uhr des anderen als verlangsamt.

Die sogenannte Zeitdilatation besagt, dass eine Uhr, die ihre Eigenzeit anzeigt und sich relativ zu einem Beobachter bewegt, bezüglich dessen Koordinatenzeit langsamer läuft, und damit auch die Zeit in diesem System selbst. Dieser Umstand kann unmittelbar aus dem nebenstehenden Minkowski-Diagramm abgelesen werden. Der Beobachter bewege sich innerhalb der Raumzeit vom Ursprung O in Richtung A und die Uhr von O in Richtung B. Alle Ereignisse, die dieser Beobachter bei A als gleichzeitig interpretiert, liegen auf der Parallelen zu seiner Wegachse, also der Geraden durch A und B. Wegen OB < OA ist jedoch auf der relativ zu ihm bewegten Uhr eine kleinere Zeit vergangen als auf der Uhr, die der Beobachter mit sich führt.

Ein zweiter Beobachter, der sich mit der einen Uhr von O nach B bewegt hat, wird jedoch behaupten, die andere Uhr befinde sich in diesem Moment erst bei C und sie sei es daher, die langsamer laufe. Die unterschiedliche Interpretation dessen, was gleichzeitig an einem anderen Ort geschieht, ist die Ursache für diese scheinbar paradoxe Situation. Angesichts des Relativitätsprinzips ist die Frage, wer die Situation korrekt beurteilt, prinzipiell nicht beantwortbar und daher sinnlos.

Längenkontraktion

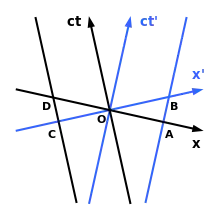
Längenkontraktion: Beide Beobachter messen die Maßstäbe des anderen als verkürzt.

Die sogenannte Längenkontraktion besagt, dass ein Längenmaßstab von einer bestimmten Ruhelänge, der sich relativ zu einem Beobachter bewegt, mit dessen Maßstäben als verkürzt gemessen wird, und damit auch der Raum in diesem System selbst. Der Beobachter bewege sich wieder auf der ct-Achse. Die Weltlinien der beiden Endpunkte eines relativ zu ihm bewegten Maßstabes bewegen sich entlang der ct′-Achse und parallel dazu durch A und B. Für den Beobachter reicht der Maßstab zur Zeit t = 0 nur von O bis A. Für einen längs der ct′-Achse mitbewegten zweiten Beobachter, für den der Maßstab ruht, hat er im Moment t′ = 0 die Ruhelänge OB. Sie erscheint also dem ersten Beobachter wegen OA < OB verkürzt.

Der mitbewegte Beobachter wird einwenden, dass der erste Beobachter Anfangs- und Endpunkt bei O und A und damit gar nicht gleichzeitig erfasst habe, sodass er aufgrund seiner zwischenzeitlichen Bewegung eine falsche Länge ermittelt habe. Über die gleiche Argumentation ermittelt der zweite Beobachter für die Länge eines Maßstabes, dessen Endpunkte sich entlang der ct-Achse und parallel dazu durch C und D bewegen, eine Längenkontraktion von OD auf OC. Die scheinbar paradoxe Situation, dass für jeden die Maßstäbe des anderen als verkürzt gemessen werden, beruht wiederum auf der Relativität der Gleichzeitigkeit, wie das Minkowski-Diagramm zeigt.

Bei allen diesen Betrachtungen wurde vorausgesetzt, dass die Beobachter bei ihren Aussagen die ihnen bekannte Ausbreitungsgeschwindigkeit des Lichtes berücksichtigen. Das heißt, sie geben nicht an, was sie unmittelbar sehen, sondern das, was sie anhand der Signallaufzeit und der von ihnen ermittelten räumlichen Distanz zu den gesehenen Ereignissen für real halten.

Prinzip von der Konstanz der Lichtgeschwindigkeit

Die Geschwindigkeit des Lichtteilchens, das A passiert, wird von beiden Beobachtern gleich eingeschätzt.

Das bedeutendere der beiden Postulate der speziellen Relativitätstheorie ist das Prinzip von der Konstanz der Lichtgeschwindigkeit. Es besagt, dass die Vakuum-Lichtgeschwindigkeit in jedem Inertialsystem denselben Wert c hat, und zwar unabhängig von der Geschwindigkeit des Lichtsenders oder des Lichtempfängers. Alle Beobachter, die die Lichtgeschwindigkeit messen, kommen also, unabhängig von ihrem eigenen Bewegungszustand, zum selben Ergebnis. Diese Aussage erscheint zunächst paradox, ergibt sich aber grafisch unmittelbar aus dem Minkowski-Diagramm. Sie erklärt auch das Ergebnis des Michelson-Morley-Experiments, das vor der Entdeckung der Relativitätstheorie für Verwunderung sorgte.

Für Weltlinien zweier Lichtteilchen, die den Ursprung in unterschiedliche Richtungen passieren, gilt x = ct und x = −ct, das heißt, jedem Bahnpunkt entsprechen betragsmäßig gleiche Abschnitte auf der x- und der ct-Achse. Aus der Regel zur Ablesung von Koordinaten in einem schiefwinkligen Koordinatensystem ergibt sich damit, dass diese Weltlinien die beiden Winkelhalbierenden der x- und ct-Achse sind. Dem Minkowski-Diagramm entnimmt man nun, dass sie auch gleichzeitig die Winkelhalbierenden der x′- und ct′-Achse sind. Das heißt, beide Beobachter ermitteln für den Betrag der Geschwindigkeit dieser beiden Lichtteilchen denselben Wert c.

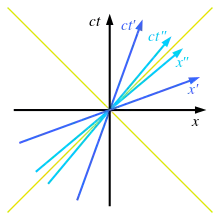
Minkowski-Diagramm für drei Koordinatensysteme. Es gilt v′ = 0,4 c und v′′ = 0,8 c relativ zu dem ungestrichenen System.

Im Prinzip lassen sich in dieses Minkowski-Diagramm weitere Koordinatensysteme zu Beobachtern mit beliebiger Geschwindigkeit hinzufügen. Bei allen diesen Koordinatensystemen bilden die Weltlinien von Lichtteilchen die Winkelhalbierenden der Koordinatenachsen. Je mehr sich die Relativgeschwindigkeiten der Lichtgeschwindigkeit nähern, umso mehr schmiegen sich die Koordinatenachsen mindestens eines der beteiligten Systeme an die Winkelhalbierende an. Die Wegachsen sind stets flacher als diese Winkelhalbierenden und die Zeitachsen stets steiler. Die Maßstäbe auf den jeweiligen Weg- und Zeitachsen sind stets gleich, unterscheiden sich jedoch im Allgemeinen von denen der anderen Koordinatensysteme.

Lichtgeschwindigkeit und Kausalität

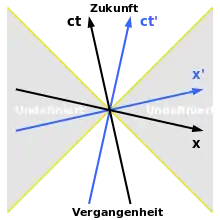
Vergangenheit und Zukunft in Bezug auf den Koordinatenursprung. Eine entsprechende zeitliche Einordnung der Ereignisse im grauen Bereich ist nicht möglich.

Alle Geraden durch den Ursprung, die steiler als die beiden Weltlinien der Lichtteilchen verlaufen, entsprechen Objekten, die sich langsamer als mit Lichtgeschwindigkeit bewegen. Da die Weltlinien der Lichtteilchen für alle Beobachter identisch sind, gilt diese Aussage unabhängig vom Beobachter. Vom Ursprung aus kann jeder Punkt oberhalb und zwischen den Weltlinien der beiden Lichtteilchen mit Unterlichtgeschwindigkeit erreicht werden, sodass jedes entsprechende Ereignis dort mit dem Ursprung in einer Ursache-Wirkungs-Beziehung stehen kann. Dieser Bereich wird als absolute Zukunft bezeichnet, da jedes dortige Ereignis unabhängig vom Beobachter später stattfindet als das Ereignis, das den Ursprung markiert, wovon man sich auf grafischem Wege leicht überzeugen kann.

Analog ist der Bereich unterhalb des Ursprungs und zwischen den Weltlinien der beiden Lichtteilchen die absolute Vergangenheit bezüglich des Ursprungs. Jedes Ereignis dort kann Ursache einer Wirkung am Ursprung sein und befindet sich eindeutig in der Vergangenheit.

Das Verhältnis zweier Ereignispunkte, die in dieser Weise in einer Ursache-Wirkungs-Beziehung stehen können, wird auch als zeitartig bezeichnet, da sie für alle Beobachter einen endlichen zeitlichen Abstand aufweisen. Dagegen stellt die Verbindungsstrecke stets die Zeitachse eines möglichen Koordinatensystems dar, für dessen Beobachter die beiden Ereignisse damit am selben Ort stattfinden. Lassen sich zwei Ereignisse gerade mit Lichtgeschwindigkeit verbinden, so nennt man sie lichtartig.

Zwei Ereignispunkte, die in keiner Weise in einer Ursache-Wirkungs-Beziehung stehen können, da sie nur mit Überlichtgeschwindigkeit verbunden werden können, haben keine allgemein definierte zeitliche Beziehung zueinander, vielmehr ist je nach Beobachter der eine oder der andere früher oder beide sind gleichzeitig. Andererseits können sie für keinen Beobachter am gleichen Ort (zu verschiedener Zeit) stattfinden (absolutes Anderswo), besitzen also eine raumartige Beziehung zueinander.

Im Prinzip lässt sich dem Minkowski-Diagramm eine weitere Raumdimension hinzufügen, sodass eine dreidimensionale Darstellung entsteht. In diesem Fall werden die Bereiche von Vergangenheit und Zukunft zu Kegeln, deren Spitzen sich im Ursprung berühren. Sie werden als Lichtkegel bezeichnet.

Lichtgeschwindigkeit als Grenze

Senden einer Nachricht mit Überlichtgeschwindigkeit von O über A nach B in die eigene Vergangenheit. Beide Beobachter beurteilen die zeitliche Reihenfolge der Ereignispaare O und A sowie A und B jedoch verschieden.

Analog würden alle Geraden durch den Ursprung, die flacher als die beiden Weltlinien der Lichtteilchen verlaufen, Objekten oder Signalen entsprechen, die sich mit Überlichtgeschwindigkeit bewegen, und zwar mit dem obigen Argument wiederum unabhängig vom Beobachter. Damit kann zwischen allen Ereignissen außerhalb der Lichtkegel und dem am Ursprung selbst mit Lichtgeschwindigkeit kein Kontakt hergestellt werden. Das Verhältnis zweier solcher Ereignispunkte wird auch als raumartig bezeichnet, da sie für alle Beobachter einen endlichen Abstand aufweisen. Dagegen stellt die Verbindungsstrecke stets die Wegachse eines möglichen Koordinatensystems dar, für dessen Beobachter die beiden Ereignisse damit gleichzeitig stattfinden. Durch leichte Variation der Geschwindigkeit dieses Koordinatensystems in beide Richtungen lassen sich daher stets zwei Koordinatensysteme finden, deren Beobachter die zeitliche Reihenfolge dieser beiden Ereignisse unterschiedlich beurteilen.

Ausgehend vom Postulat der konstanten Lichtgeschwindigkeit würde Überlichtgeschwindigkeit daher bedeuten, dass zu jedem Beobachter, für den sich ein derartiges Objekt von X nach Y bewegen würde, sich ein anderer finden ließe, für den es sich von Y nach X bewegen würde, wiederum ohne dass die Frage, wer die Situation korrekt beschreibt, einen Sinn ergäbe. Das Kausalitätsprinzip wäre damit verletzt.

Darüber hinaus folgt aus der Relativitätstheorie, dass sich mit überlichtschnellen Signalen Informationen in die eigene Vergangenheit senden ließen. So schickt in nebenstehendem Diagramm der Beobachter im x-ct-System eine Nachricht mit Überlichtgeschwindigkeit von O nach A. Im Punkt A wird es von einem Beobachter im x′-ct′-System empfangen, der wiederum ein Antwortsignal mit Überlichtgeschwindigkeit zurückschickt, sodass es bei B und damit in der Vergangenheit von O eintrifft. Die Absurdität des Vorganges wird dadurch deutlich, dass beide Beobachter anschließend behaupten müssten, die Antwort auf ihre Nachricht schon vor deren Absenden erhalten zu haben.

Die Unvereinbarkeit von Relativitätstheorie und der Möglichkeit, einen Beobachter auf Lichtgeschwindigkeit oder gar darüber hinaus zu beschleunigen, äußert sich auch in dem Umstand, dass bei Lichtgeschwindigkeit seine Zeit- und Wegachse mit der Winkelhalbierenden zusammenfallen würden, sodass das Koordinatensystem als solches kollabieren würde.

Diese Überlegungen zeigen grafisch anhand des Minkowski-Diagramms, dass die Unüberwindlichkeit der Lichtgeschwindigkeit eine Folge der relativistischen Struktur von Raum und Zeit darstellt und keine Eigenschaft der Dinge, wie beispielsweise eines lediglich unvollkommenen Raumschiffes.

Die Verwandtschaft von Raum und Zeit

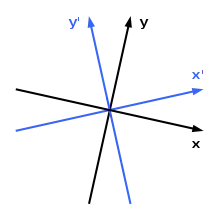
Drehung eines rechtwinkligen Koordinatensystems im Raum. Sie ist formal verwandt mit der Scherung von Raum- und Zeitkoordinaten in der Relativitätstheorie.

Raum und Zeit erscheinen in den Grundgleichungen der Relativitätstheorie formal weitgehend gleichwertig nebeneinander und lassen sich daher zu einer vierdimensionalen Raumzeit vereinigen. Diese enge Verwandtschaft von Raum und Zeit zeigt sich auch im Minkowski-Diagramm.

Die bekannte Gleichwertigkeit der drei Dimensionen des Raumes äußert sich insbesondere in der Möglichkeit, sich im Raum zu drehen. Damit sind die drei Dimensionen nicht fest vorgegeben, sondern über die Definition eines Koordinatensystems frei wählbar. Raum und Zeit erscheinen dagegen in der newtonschen Physik strikt getrennt. In der speziellen Relativitätstheorie erweisen sich jedoch Relativbewegungen als eng verwandt mit Drehungen von Koordinatensystemen mit Raum- und Zeitachsen in der Raumzeit: Da der Winkel zwischen den beiden Raum- und den beiden Zeitachsen in der symmetrischen Darstellung gleich ist, steht die x-Achse senkrecht auf der ct′-Achse und ebenso die x′-Achse auf der ct-Achse. Die Anordnung der vier Achsen ist damit identisch mit der zweier gewöhnlicher rechtwinkliger Koordinatensysteme, die lediglich um den Winkel φ gegeneinander gedreht wurden mit anschließender Vertauschung der beiden Zeitachsen. Damit ergibt sich eine Scherung der Achsen anstelle einer Drehung. Diese Vertauschung zweier Achsen sowie sämtliche Unterschiede zwischen Raum und Zeit lassen sich letztlich auf ein einziges Vorzeichen in der Gleichung zurückführen, die Raum und Zeit verknüpft, indem sie die Metrik der Raumzeit definiert.

Aus diesem Grund besteht die Bedeutung der Lichtgeschwindigkeit als fundamentaler Naturkonstante der Physik in erster Linie darin, diese Verbindung zwischen Raum und Zeit herzustellen. Der Umstand, dass sich Photonen mit dieser Geschwindigkeit bewegen, ist eher als Konsequenz dieser engen Verwandtschaft anzusehen. In der Relativitätstheorie ist es daher auch üblich, anstelle der Koordinaten x, y, z und t mit x₁ bis x₄ zu rechnen, wobei x₄ = ct. Alle Formeln vereinfachen sich damit erheblich, und für die Lichtgeschwindigkeit ergibt sich in diesen Einheiten eine dimensionslose Zahl c = 1.

Siehe auch

Minkowski-Raum

Einzelnachweise

Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. 322, Nr. 10, 1905, S. 891–921.
Hermann Minkowski: Raum und Zeit. Vortrag, gehalten auf der 80. Naturforscher-Versammlung zu Köln am 21. September 1908. In: Jahresbericht der Deutschen Mathematiker-Vereinigung 1909.
Jürgen Freund: Spezielle Relativitätstheorie für Studienanfänger. vdf Hochschulverlag, 2007, ISBN 3-8252-2884-3, S. 39.
Dmitry Mirimanoff: La transformation de Lorentz-Einstein et le temps universel de M. Ed. Guillaume. In: Archives des sciences physiques et naturelles (supplement). 3, 1921, S. 46–48.
Albert Shadowitz: The Electromagnetic Field, Reprint of 1975 edition. Auflage, Courier Dover Publications, 2012, ISBN 0-486-13201-3, S. 460. Siehe eingeschränkte Vorschau in der Google-Buchsuche.
Leo Sartori: Understanding Relativity: a simplified approach to Einstein’s theories. University of California Press, 1996, ISBN 0-520-20029-2, S. 151 ff.
Paul Gruner, Josef Sauter: Représentation géométrique élémentaire des formules de la théorie de la relativité. In: Archives des sciences physiques et naturelles. 3, 1921, S. 295–296.
Paul Gruner: Eine elementare geometrische Darstellung der Transformationsformeln der speziellen Relativitätstheorie. In: Physikalische Zeitschrift. 22, 1921, S. 384–385.
Max Born: Die Relativitätstheorie Einsteins, Erste Ausgabe. Auflage, Springer, Berlin 1920, S. 177–180.
7. Ausgabe: Max Born: Die Relativitätstheorie Einsteins. Springer, Berlin-Heidelberg-New York 1964/2003, ISBN 3-540-00470-X, S. 212–216.
Paul Gruner: Elemente der Relativitätstheorie. P. Haupt, Bern 1922.
Paul Gruner: Graphische Darstellung der speziellen Relativitätstheorie in der vierdimensionalen Raum-Zeit-Welt I. In: Zeitschrift für Physik. 10, Nr. 1, 1922, S. 22–37. doi:10.1007/BF01332542.
Paul Gruner: Graphische Darstellung der speziellen Relativitätstheorie in der vierdimensionalen Raum-Zeit-Welt II. In: Zeitschrift für Physik. 10, Nr. 1, 1922, S. 227–235. doi:10.1007/BF01332563.
Paul Gruner: a) Représentation graphique de l’univers espace-temps à quatre dimensions. b) Représentation graphique du temps universel dans la théorie de la relativité. In: Archives des sciences physiques et naturelles. 4, 1921, S. 234–236.
Paul Gruner: Die Bedeutung „reduzierter“ orthogonaler Koordinatensysteme für die Tensoranalysis und die spezielle Relativitätstheorie. In: Zeitschrift für Physik. 10, Nr. 1, 1922, S. 236–242. doi:10.1007/BF01332564.
Paul Gruner: Geometrische Darstellungen der speziellen Relativitätstheorie, insbesondere des elektromagnetischen Feldes bewegter Körper. In: Zeitschrift für Physik. 21, Nr. 1, 1924, S. 366–371. doi:10.1007/BF01328285.
Enrique Loedel: Aberracion y Relatividad. In: Anales Sociedad Científica Argentina. 145, 1948, S. 3–13.
Fisica relativista. Kapelusz Editorial, Buenos Aires, Argentina (1955).
Henri Amar: New Geometric Representation of the Lorentz Transformation. In: American Journal of Physics. 23, Nr. 8, 1955, S. 487–489. doi:10.1119/1.1934074.
Henri Amar, Enrique Loedel: Geometric Representation of the Lorentz Transformation. In: American Journal of Physics. 25, Nr. 5, 1957, S. 326–327. doi:10.1119/1.1934453.
Albert Shadowitz: Special relativity, Reprint of 1968 edition. Auflage, Courier Dover Publications, 1988, ISBN 0-486-65743-4, S. 20–22.

Weblinks

Commons: Minkowski-Diagramm – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Spezielle Relativitätstheorie – Lern- und Lehrmaterialien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. 322, Nr. 10, 1905, S. 891–921.

[2] Hermann Minkowski: Raum und Zeit. Vortrag, gehalten auf der 80. Naturforscher-Versammlung zu Köln am 21. September 1908. In: Jahresbericht der Deutschen Mathematiker-Vereinigung 1909.

[3] Jürgen Freund: Spezielle Relativitätstheorie für Studienanfänger. vdf Hochschulverlag, 2007, ISBN 3-8252-2884-3, S. 39.

[mirimanoff-4] Dmitry Mirimanoff: La transformation de Lorentz-Einstein et le temps universel de M. Ed. Guillaume. In: Archives des sciences physiques et naturelles (supplement). 3, 1921, S. 46–48.

[5] Albert Shadowitz: The Electromagnetic Field, Reprint of 1975 edition. Auflage, Courier Dover Publications, 2012, ISBN 0-486-13201-3, S. 460. Siehe eingeschränkte Vorschau in der Google-Buchsuche.

[sartori-6] Leo Sartori: Understanding Relativity: a simplified approach to Einstein’s theories. University of California Press, 1996, ISBN 0-520-20029-2, S. 151 ff.

[gruner1-7] Paul Gruner, Josef Sauter: Représentation géométrique élémentaire des formules de la théorie de la relativité. In: Archives des sciences physiques et naturelles. 3, 1921, S. 295–296.

[gruner2-8] Paul Gruner: Eine elementare geometrische Darstellung der Transformationsformeln der speziellen Relativitätstheorie. In: Physikalische Zeitschrift. 22, 1921, S. 384–385.

[9] Max Born: Die Relativitätstheorie Einsteins, Erste Ausgabe. Auflage, Springer, Berlin 1920, S. 177–180.
7. Ausgabe: Max Born: Die Relativitätstheorie Einsteins. Springer, Berlin-Heidelberg-New York 1964/2003, ISBN 3-540-00470-X, S. 212–216.

[gruner3-10] Paul Gruner: Elemente der Relativitätstheorie. P. Haupt, Bern 1922.

[gruner4-11] Paul Gruner: Graphische Darstellung der speziellen Relativitätstheorie in der vierdimensionalen Raum-Zeit-Welt I. In: Zeitschrift für Physik. 10, Nr. 1, 1922, S. 22–37. doi:10.1007/BF01332542.

[gruner5-12] Paul Gruner: Graphische Darstellung der speziellen Relativitätstheorie in der vierdimensionalen Raum-Zeit-Welt II. In: Zeitschrift für Physik. 10, Nr. 1, 1922, S. 227–235. doi:10.1007/BF01332563.

[gruner6-13] Paul Gruner: a) Représentation graphique de l’univers espace-temps à quatre dimensions. b) Représentation graphique du temps universel dans la théorie de la relativité. In: Archives des sciences physiques et naturelles. 4, 1921, S. 234–236.

[gruner7-14] Paul Gruner: Die Bedeutung „reduzierter“ orthogonaler Koordinatensysteme für die Tensoranalysis und die spezielle Relativitätstheorie. In: Zeitschrift für Physik. 10, Nr. 1, 1922, S. 236–242. doi:10.1007/BF01332564.

[gruner8-15] Paul Gruner: Geometrische Darstellungen der speziellen Relativitätstheorie, insbesondere des elektromagnetischen Feldes bewegter Körper. In: Zeitschrift für Physik. 21, Nr. 1, 1924, S. 366–371. doi:10.1007/BF01328285.

[loed48-16] Enrique Loedel: Aberracion y Relatividad. In: Anales Sociedad Científica Argentina. 145, 1948, S. 3–13.

[17] Fisica relativista. Kapelusz Editorial, Buenos Aires, Argentina (1955).

[18] Henri Amar: New Geometric Representation of the Lorentz Transformation. In: American Journal of Physics. 23, Nr. 8, 1955, S. 487–489. doi:10.1119/1.1934074.

[19] Henri Amar, Enrique Loedel: Geometric Representation of the Lorentz Transformation. In: American Journal of Physics. 25, Nr. 5, 1957, S. 326–327. doi:10.1119/1.1934453.

[20] Albert Shadowitz: Special relativity, Reprint of 1968 edition. Auflage, Courier Dover Publications, 1988, ISBN 0-486-65743-4, S. 20–22.