Relativität der Gleichzeitigkeit
Die Relativität der Gleichzeitigkeit ist eine Aussage der speziellen Relativitätstheorie. Sie besagt, dass es auf die Frage, ob zwei Ereignisse an verschiedenen Orten gleichzeitig oder zu verschiedenen Zeitpunkten stattfinden, keine für alle Beobachter gleichermaßen gültige Antwort gibt.
Erläuterung
Gleichzeitigkeit ist ein grundlegender Begriff in der Physik. Alle Aussagen über Zeitabläufe beruhen auf Zeitvergleichen und somit auf dem Begriff Gleichzeitigkeit. Ein Beobachter kann jederzeit problemlos erkennen, ob in seiner unmittelbaren Umgebung zwei Ereignisse gleichzeitig stattfinden oder nicht. Bei weiter entfernten Ereignissen ist dies nicht ohne weiteres der Fall.
Im Rahmen der newtonschen Physik scheint es möglich, ein einheitliches Zeitsystem zu definieren, das für das gesamte Universum gilt. Damit ist gemeint, dass zwei Beobachter zwar unter Umständen verschiedene Zeitpunkte für bestimmte Ereignisse messen, dass sich aber diese Zeitpunkte eindeutig einander zuordnen lassen, so dass klar ist, welche Ereignisse gleichzeitig stattfinden und welche nicht, unabhängig davon, wo sich diese Beobachter befinden und in welcher Weise sie sich bewegen. Man spricht in diesem Zusammenhang von einer „absoluten“ Zeit. Gäbe es eine absolute Zeit, so wären sich auch alle Beobachter über die Reihenfolge von Ereignissen einig. Insbesondere hätten sie dieselbe Vorstellung von Vergangenheit, Gegenwart und Zukunft. Erst in der speziellen Relativitätstheorie wird die Existenz einer universell gültigen Zeit – und somit eines universellen Verständnisses von Gleichzeitigkeit – widerlegt.
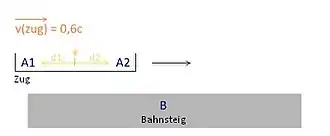
Ausgangspunkt für die spezielle Relativitätstheorie ist die durch zahlreiche Beobachtungen bestätigte Tatsache, dass die Messung der Lichtgeschwindigkeit in jedem Inertialsystem und unter allen Umständen stets denselben Wert liefert. Man spricht von der „Invarianz der Lichtgeschwindigkeit“. Unter dieser Voraussetzung machen wir folgendes Gedankenexperiment: Ein Zug fährt mit hoher Geschwindigkeit durch einen Bahnhof. Nun wird im Zug mittig zwischen zwei mitgeführten Uhren A1 und A2 ein Lichtblitz ausgelöst, wobei bei Ankunft der Lichtblitze an den Uhren die jeweilige Uhr zu laufen beginnt. Da die Lichtgeschwindigkeit in jedem Inertialsystem in allen Richtungen gleich groß ist (siehe oben), wird ein Fahrgast des Zuges, also ein Beobachter im Ruhesystem des Zuges, durch späteren Uhrenvergleich feststellen, dass A1 und A2 von den Lichtblitzen gleichzeitig erreicht wurden und die beiden Uhren somit synchron zu laufen begannen. Vom Standpunkt eines Beobachters im Ruhesystem des Bahnhofes sieht die Reihenfolge der Ereignisse aber anders aus. Um den Zeitpunkt der Ankunft der Lichtblitze bei A1 und A2 genau bestimmen zu können, hat er mit Lichtsignalen synchronisierte und mit Sensoren ausgestattete Uhren am Bahnsteig befestigt. Für diesen Beobachter bewegt sich der Zug mit hoher Geschwindigkeit (in der Abbildung Durchfahrt von links nach rechts). Daraus folgt, dass der Blitz zu A2 einen längeren Weg zurücklegen muss als zu A1, weil A2 sich von der Stelle, von der der Blitz ausgegangen ist, fortbewegt, wohingegen A1 sich auf diese Stelle zubewegt. Die an den Gleisen befestigten Uhren werden folglich anzeigen, dass A1 zeitlich vor A2 vom Blitz getroffen wurde und früher zu laufen begann. A1 und A2 sind aus Sicht des Ruhesystems des Bahnhofes also nicht synchron.
Die Relativität der Gleichzeitigkeit besagt somit, dass an unterschiedlichen Orten stattfindende Ereignisse, die in einem Inertialsystem gleichzeitig sind, aus Sicht eines relativ dazu bewegten Inertialsystems nicht gleichzeitig sind. Die Diskrepanz ist umso größer, je höher die Relativgeschwindigkeit und je größer der räumliche Abstand der Ereignisse ist. Wichtig dabei ist, dass die Messungen in allen Inertialsystemen unmittelbar am Ort der Ereignisse mittels synchronisierter Uhren durchgeführt wurden.
Kausalität sowie Zukunft und Vergangenheit im Minkowski-Raum
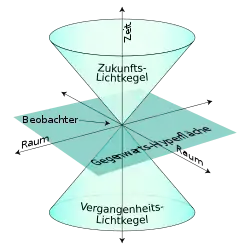
Unter Kausalität versteht man die eindeutige Beziehung von Ursache und Wirkung. Ein Ereignis kann nur dann die Ursache für ein zweites Ereignis sein, wenn es zeitlich vor ihm eintritt. Da aber die Reihenfolge von Ereignissen vom Beobachter (bzw. von dessen Bewegungszustand) abhängt, könnte dies zu Problemen mit der Kausalität führen. Denn wenn in einem Bezugssystem Ereignis A vor Ereignis B eintritt, im anderen Bezugssystem jedoch Ereignis B vor Ereignis A, dann folgt daraus, dass sowohl A Ursache von B, als auch B Ursache von A sein könnte. Damit lassen sich Paradoxien konstruieren, bei denen ein Ereignis sich selbst in der Vergangenheit rückwirkend verhindert. Außerdem wären Zeitreisen mit Überlichtgeschwindigkeit möglich. Man reist von A zum späteren Ereignis B. Dann wechselt man durch normale Beschleunigung in ein Bezugssystem, in dem A später als B stattfindet. Anschließend reist man wiederum mit Überlichtgeschwindigkeit von B zu einem Ereignis vor A. Dies ist einer der Gründe dafür, warum generell angenommen wird, dass Überlichtgeschwindigkeit nicht möglich ist.
Die Lichtgeschwindigkeit stellt also eine Maximalgeschwindigkeit dar, und die Raumzeit zerfällt in drei Bereiche: Aus Sicht eines Beobachters gibt es eine Zukunft, die von ihm beeinflussbar ist, eine Vergangenheit, deren Auswirkungen ihn betreffen und ein „Anderswo“, mit dem er in keiner kausalen Beziehung steht. Diese drei Bereiche werden im Minkowski-Raum durch den Doppelkegel des Lichts voneinander getrennt. Da die Lichtgeschwindigkeit invariant ist, ist die Zuordnung von Ereignissen zu einem der drei Bereiche für alle Beobachter gleich. Das bedeutet, dass verschiedene Beobachter zwar die Gleichzeitigkeit und die Reihenfolge von manchen Ereignissen unterschiedlich bewerten können (nämlich dann, wenn sich eines der Ereignisse im Anderswo des anderen befindet), dass sie sich aber bezüglich der Kausalität stets einig sind. Ob ein Ereignis A die Ursache für ein Ereignis B sein kann, hängt nicht vom Bezugssystem des Beobachters ab. Insofern ist es korrekt, von einer absoluten Zukunft und einer absoluten Vergangenheit zu sprechen, wenn es auch eine absolute Gegenwart nicht gibt, außer im „Hier und Jetzt“.
Der Raumzeitpunkt des Beobachters („Hier und Jetzt“) wird im Folgenden mit A bezeichnet. Ein zweites beliebiges Ereignis mit B. Folgende Aussagen über diese beiden Ereignisse sind gültig:
- Falls B sich im Zukunftslichtkegel von A befindet: „Der Beobachter kann das Ereignis erreichen, indem er sich langsamer als das Licht bewegt.“ In diesem Fall gibt es ein Bezugssystem, in dem B am selben Ort wie A stattfindet (nämlich das Ruhesystem des Beobachters). Es gibt aber kein Bezugssystem, in dem beide Ereignisse gleichzeitig eintreten. Alle Beobachter sind sich darüber einig, dass B später als A eintritt. Diese Lage von Ereignissen zueinander nennt man zeitartig.
- Falls sich B auf der Oberfläche des Zukunftslichtkegels von A befindet: „Der Beobachter könnte das Ereignis B nur erreichen, wenn er sich mit Lichtgeschwindigkeit bewegen würde.“ Auch in diesem Fall sind sich alle Beobachter über die Reihenfolge von A und B einig. Es gibt weder ein Bezugssystem, in dem beide Ereignisse am gleichen Ort, noch ein Bezugssystem, in dem beide Ereignisse zur selben Zeit stattfinden. Diese Lage der Ereignisse zueinander nennt man lichtartig.
- Falls sich B außerhalb der beiden Lichtkegel von A befindet: „Nichts kann von B nach A oder von A nach B gelangen, denn dafür müsste es sich mit Überlichtgeschwindigkeit bewegen.“ In diesem Fall gibt es ein Bezugssystem, in dem beide Ereignisse zur selben Zeit stattfinden, sich also nur im Ort unterscheiden. Es gibt aber kein Bezugssystem, in dem beide Ereignisse am gleichen Ort stattfinden. Daher nennt man diese Lage von Ereignissen zueinander raumartig. In diesem – und nur in diesem – Fall ist die zeitliche Reihenfolge der Ereignisse vom Bewegungszustand des Beobachters abhängig. Hinsichtlich der Kausalität spielt das aber keine Rolle, da alle Beobachter auch darin übereinstimmen, dass keines der Ereignisse Ursache des anderen Ereignisses sein kann.
Der beschleunigte Beobachter
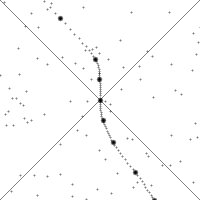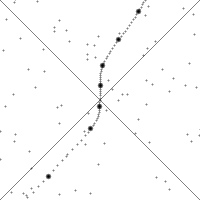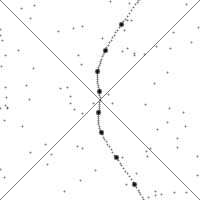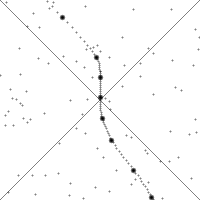
Die Animation links demonstriert, wie sich die Minkowski-Raumzeit für einen beschleunigten Beobachter darstellt. Die punktierte Linie stellt dabei die Weltlinie des Beobachters dar, der sich jeweils in der Mitte des Bildes befindet. Die dicken Punkte markieren gleiche (Eigen)zeitintervalle. Dehnung und Stauchung der Weltlinie zeigen Beschleunigung des Beobachters in Bewegungsrichtung, Krümmung Beschleunigung quer dazu. Das Diagramm zeigt die Welt zu jedem Zeitpunkt im Inertialsystem, also aus Sicht des Beobachters. Bei den Beschleunigungen kann man beobachten, dass Punkte der Raumzeit nach oben, also entgegen dem „Zeitfluss“, laufen. Jedoch überqueren sie dabei niemals den Lichtkegel (die Diagonallinien) von unten; dieser wird durch den Zeitablauf stets nur nach unten durchquert. Somit kann ein Punkt niemals in den Vorwärtslichtkegel eintreten (man kann durch Beschleunigung kein Ereignis in die absolute Zukunft versetzen) und niemals den Rückwärtslichtkegel verlassen (man kann Ereignisse durch Beschleunigung nicht aus der absoluten Vergangenheit herausholen).
Man sieht auch, dass die Weltlinie des Beobachters stets innerhalb des Lichtkegels verläuft. Ereignisse, die den Beobachter erreichen bzw. erreicht haben, liegen stets in seiner absoluten Zukunft bzw. Vergangenheit; die Reihenfolge dieser Ereignisse lässt sich durch Beschleunigung nicht verändern. Insbesondere kann der Beobachter vergangene Ereignisse nicht zu zukünftigen Ereignissen machen.
Gleichzeitigkeit im Alltag
Für menschliche Alltagserfahrung spielen relativistische Effekte der Gleichzeitigkeit keine Rolle: Selbst wenn man auf dem Mount Everest stünde und aufs Meer hinaussehen könnte, wäre für den gesamten sichtbaren Bereich der Erdoberfläche bis zum Horizont die Relativität der Gleichzeitigkeit auf einen Bereich von wenigen Millisekunden beschränkt. Dieses Zeitintervall liegt unterhalb der Schwelle, ab der Menschen überhaupt in der Lage sind, die Reihenfolge von Ereignissen aufzulösen, und unterhalb der Schwelle, ab der Menschen optische Eigenschaften als nichtgleichzeitig wahrnehmen können. Für die Alltagserfahrung ist das Licht stets derart schnell, dass der Eindruck einer Gleichzeitigkeit der Ereignisse entsteht.
Literatur
- Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 1905, S. 891–921 (als Faksimile (PDF; 1,9 MB); als digitalisierter Volltext bei Wikilivres; und kommentiert und erläutert bei Wikibooks)
- P. Mittelstaedt: Der Zeitbegriff in der Physik. 1980, ISBN 3-411-01585-3
- H. Reichenbach: Axiomatik der relativistischen Raum-Zeit-Lehre. Vieweg, Braunschweig 1924
- H. Reichenbach: Philosophie der Raum-Zeit-Lehre. de Gruyter, Berlin & Leipzig, 1928
Weblinks
- Detaillierte Beschreibung der Relativität der Gleichzeitigkeit (englisch).
- Was ist Gleichzeitigkeit? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 10. Juni 2001.