Wellenoptik

Als Wellenoptik oder physikalische Optik bezeichnet man in der Physik den Teilbereich der Optik, der Licht als elektromagnetische Welle behandelt. Mithilfe der Wellenoptik lassen sich Eigenschaften wie Farbe, Interferenzfähigkeit, Beugung und Polarisation des Lichtes erklären, die mit geometrischer Optik nicht erklärbar sind.

Geschichte

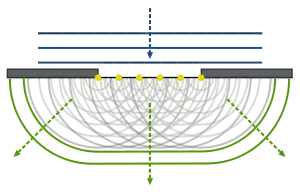
Beugung am Spalt gemäß dem Huygensschen Prinzip. Die gelben Punkte zeigen dabei die gedachten Ausgangspunkte für neue Wellen.

Bereits im 17. Jahrhundert erkannte man, dass die klassische Deutung von Licht als Bündel geradliniger Strahlen unvollständig sein muss. Beugung und Interferenz lassen sich so nicht erklären. Christiaan Huygens bemerkte um 1650, dass eine Lichtausbreitung analog zu Wasserwellen die Phänomene erklären würde. Er formulierte sein Huygenssches Prinzip, welches besagt, dass von jedem Punkt einer beugenden Fläche kugelförmige Elementarwellen ausgehen, die sich überlagern und so die beobachtbaren Beugungseffekte hervorrufen. Zunächst wurde Huygens nicht ernst genommen, da man die Korpuskeltheorie von Isaac Newton favorisierte. Erst im 19. Jahrhundert wurde die Wellentheorie (auch als Undulationstheorie bezeichnet) durch das Doppelspaltexperiment von Thomas Young bestätigt. Die Arbeiten von Joseph von Fraunhofer und Augustin Jean Fresnel bauten die Theorie weiter aus. Friedrich Magnus Schwerd wandte die Wellentheorie zur Erklärung seiner umfassenden Beugungsexperimente an.

Grundlagen

Bei Betrachtung der Wechselwirkungen von Licht mit Materie wurden verschiedene Effekte beobachtet, die sich nicht mehr mit geometrischer Optik erklären lassen. So bilden sich hinter Öffnungen – wie auch hinter Kanten generell – beim Durchgang paralleler Lichtstrahlen (genügend weit entfernte bzw. punktförmige Lichtquelle) im Schattenbereich helle Streifen mit abnehmender Intensität. Das Licht wird gebeugt. Bei Mehrfachspalten mit Spaltabständen in der Größenordnung der Wellenlänge des verwendeten Lichts treten Überlagerungen der an den einzelnen Kanten gebeugten Teilwellen auf. Diese Teilwellen interferieren miteinander. Im Fall sehr kurzer Wellenlängen bzw. sehr großer Objekte ist die Beugung des Lichts vernachlässigbar und es wird mit den Gesetzen der Strahlenoptik (= der geometrischen Optik) gerechnet. In der Wellenoptik wird Licht durch eine Transversalwelle mit Wellenlänge, Amplitude und Phase beschrieben. Jede Welle wird mathematisch als Lösung einer Wellengleichung dargestellt:

\Delta u({\vec {r}},t)={\frac {1}{c^{2}}}{\frac {\partial ^{2}u({\vec {r}},t)}{\partial t^{2}}}

Dabei ist $\Delta$ der Laplace-Operator, c die Lichtgeschwindigkeit und u die von Ort ${\vec {r}}$ und Zeit t abhängende Wellenfunktion. Die Wellenfunktion kann dabei entweder skalar oder vektoriell sein. Die vektorielle Beschreibung des Lichts ist notwendig, wenn die Polarisation eine Rolle spielt. Ansonsten ist die skalare Beschreibung die einfachere.

Übergang zur Geometrischen Optik

Die Wellengleichung ist äquivalent zur Helmholtzgleichung, da beide über die Fouriertransformation in der Zeit $t$ bzw. Frequenz $\omega$ zusammenhängen:

\left(\Delta +{\frac {\omega ^{2}}{c^{2}}}\right){\hat {u}}({\vec {r}},\omega )=0

.

Dabei ist ${\hat {u}}({\vec {r}},\omega )$ die Fouriertransformierte von $u({\vec {r}},t)$ . Führt man die Wellenzahl $k=\omega /c$ ein, so ergibt sich die Helmholtzgleichung

\left(\Delta +k^{2}\right){\hat {u}}({\vec {r}},k)=0

.

Eine Lösung dieser Gleichung ergibt sich aus dem Ansatz

u({\vec {r}},k)=a({\vec {r}})e^{ikS({\vec {r}})},

unter der Näherung, dass die Amplitude $a({\vec {r}})$ nur langsam veränderlich ist, d. h., über eine Strecke in der Größenordnung der Wellenlänge $\lambda ={\frac {2\pi }{k}}$ als konstant betrachtet werden kann.

Die Flächen $kS({\vec {r}})=\mathrm {const}$ bestimmen die Flächen gleicher Phase (= Wellenfronten). Für $S({\vec {r}})=x$ würde sich z. B. eine ebene Welle ergeben. Das Gradientenfeld $\nabla S({\vec {r}})$ gibt die Ausbreitungsrichtung der einzelnen Punkte der Wellenfront an. Im Beispiel der ebenen Welle ist das Gradientenfeld $\nabla x=(1,0,0)^{T}$ und die Wellenfronten breiten sich in x-Richtung aus. In der Nähe eines Punktes ${\vec {r}}_{0}$ kann jede, durch obige Lösung beschriebene Welle, als ebene Welle mit Wellenzahl $k_{0}=k/n({\vec {r}}_{0})$ (Brechungsindex $n({\vec {r}}_{0})$ an dieser Stelle) und Ausbreitungsrichtung ${\hat {\vec {k}}}\propto \nabla S({\vec {r}})|_{{\vec {r}}_{0}}$ aufgefasst werden. $S({\vec {r}})$ heißt Eikonal und ist eine wichtige Funktion in der geometrischen Optik, denn sie bestimmt die lokalen Wellenvektoren der Welle (Ausbreitungsrichtung mal Wellenzahl). Die Strahlengänge in der geometrischen Optik sind mit den lokalen Wellenvektoren identisch.[1] Unter der angegebenen Näherung kann durch Einsetzen des Ansatzes in die Helmholtzgleichung die Eikonalgleichung gewonnen werden:

(\nabla S({\vec {r}}))^{2}=n^{2}({\vec {r}})

.

Diese Gleichung besagt, dass der Brechungsindex $n$ die Phase der Welle bestimmt und bildet die formale Grundlage der geometrischen Optik:

Die Näherung, dass die Amplitude der Welle in der Größenordnung der Wellenlänge nicht stark variiert, entspricht der üblichen Aussage, dass die geometrische Optik gültig ist, solange die streuenden Objekte sehr viel größer als die Wellenlänge des Lichts sind.
Der lokale Brechungsindex bestimmt das Gradientenfeld der Phase und damit die lokale Ausbreitungsrichtung und Wellenzahl der Welle.

Paraxiale Strahlen

Bild der Lichtintensität eines 532-nm-Laserpointers, der auf eine Digitalkamera fokussiert ist. Es ist die dominante TEM₀₀-Mode zu sehen.

Ein großes Anwendungsgebiet der Wellenoptik befasst sich mit Lasern. Laserlicht ist einerseits nahezu monochromatisch und andererseits so stark gebündelt, dass der Lichtstrahl für große Strecken achsennah bleibt (= nicht divergiert). Solche Wellen sind Lösungen der Helmholtzgleichung unter der paraxialen Näherung. Diese besagt, dass sich die Amplitude $a({\vec {r}})$ in Ausbreitungsrichtung $z$ nicht stark ändern darf. Mathematisch bedeutet dies, dass die 2. Ableitung der Amplitude nach $z$ vernachlässigt werden darf: $\partial _{z}^{2}a({\vec {r}})\approx 0$ .

Eine wichtige Lösung, die sich unter dieser Näherung ergibt, ist die Gauß-Lösung. Im nebenstehenden Bild ist die gaußverteilte Intensitätsverteilung von Licht eines Laserpointers zu sehen.

Farbe und Intensität

Die Farbe des Lichtes entspricht seiner Wellenlänge. Monochromatisches Licht hat nur eine Wellenlänge, während Weißlicht eine Überlagerung vieler Wellen unterschiedlicher Wellenlängen darstellt. Eigentlich ist die Frequenz der Lichtwelle ausschlaggebend für die Farbe; die Wellenlänge ist abhängig von der Ausbreitungsgeschwindigkeit und somit vom Medium in dem sich das Licht ausbreitet. In den gebräuchlichen Aussagen über die Farbe von Licht im Zusammenhang mit seiner Wellenlänge wird die Ausbreitung im Vakuum vorausgesetzt. In Luft ist die Ausbreitungsgeschwindigkeit nur geringfügig kleiner als die Vakuumlichtgeschwindigkeit, sodass auch die Wellenlänge einer bestimmten Frequenz in Luft nur gering von der im Vakuum abweicht. Die Intensität des Lichtes ist proportional zum Quadrat der Amplitude dieser Welle, gemittelt über die Zeit.

Kohärenz und Interferenz

Neben der Amplitude kann man auch die Phase der Welle betrachten. Stehen mehrere Wellen in einer konstanten Phasenbeziehung, so spricht man von Kohärenz. Kohärente Wellen haben die Eigenschaft, dass sie miteinander interferieren können. Unterschiedliche Wellen überlagern sich dabei so, dass es zur Verstärkung (Wellenberg trifft auf Wellenberg – konstruktive Interferenz) oder Abschwächung (Wellenberg trifft auf Wellental – destruktive Interferenz) kommt.

Polarisation

Eine Transversalwelle schwingt zwar stets senkrecht zur Richtung der Lichtausbreitung, hat jedoch noch immer zwei Freiheitsgrade. Findet die Schwingung nur in einer Ebene statt oder ändert sie sich regelmäßig, so spricht man von polarisiertem Licht. Die Polarisation kann nur durch die vektorielle Darstellung als elektromagnetische Welle erklärt werden.

Wellenfronten

Statt Lichtstrahlen betrachtet man in der Wellenoptik das verallgemeinerte Konzept der Wellenfront. Eine Wellenfront ist eine Fläche, die Punkte gleicher Phase verschiedener Wellen in sich vereinigt. Lichtstrahlen stehen stets senkrecht auf der Wellenfront.

Grenzen der Wellenoptik

Es gibt Phänomene, die sich durch die Wellentheorie nicht erklären lassen. Dazu gehört der von Wilhelm Hallwachs 1887 entdeckte und von Albert Einstein 1905 erklärte äußere Photoeffekt (Nobelpreis 1921). Einstein erklärte die Wechselwirkung zwischen Licht und Materie mit der Lichtquantenhypothese. Man sprach dann von Welle-Teilchen-Dualismus. Der scheinbare Widerspruch, dass sich Licht sowohl wie Wellen als auch wie Teilchen verhält, ist von zentraler Bedeutung für die moderne Quantenphysik.

Literatur

Bahaa E. A. Saleh, Malvin Carl Teich: Fundamentals of Photonics. 2. Auflage. John Wiley & Sons, New Jersey 2007, ISBN 978-0-471-35832-9.
Eugene Hecht: Optik. Oldenbourg, 2005, ISBN 978-3-486-27359-5, S. 62 (eingeschränkte Vorschau in der Google-Buchsuche).

Weblinks

Commons: Wellenmechanik [2] – Sammlung von Bildern, Videos und Audiodateien

Belege

Florian Scheck: Theoretische Physik 3: Klassische Feldtheorie. Von der Elektrodynamik zu den Eichtheorien. Springer, 2005, ISBN 978-3-540-23145-5, S. 224 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 3. Januar 2012]).
Achtung: Während im Deutschen das Lemma Wellenmechanik auf die Quantenmechanik verlinkt, wird darunter im Englischen und auf Commons die hier erläuterte Wellenoptik behandelt.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Scheck2005-1] Florian Scheck: Theoretische Physik 3: Klassische Feldtheorie. Von der Elektrodynamik zu den Eichtheorien. Springer, 2005, ISBN 978-3-540-23145-5, S. 224 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 3. Januar 2012]).

[2] Achtung: Während im Deutschen das Lemma Wellenmechanik auf die Quantenmechanik verlinkt, wird darunter im Englischen und auf Commons die hier erläuterte Wellenoptik behandelt.