Kristall
Ein Kristall ist ein Festkörper, dessen Bausteine – z. B. Atome, Ionen oder Moleküle – regelmäßig in einer Kristallstruktur angeordnet sind. Bekannte kristalline Materialien sind Kochsalz, Zucker, Minerale und Schnee – aber auch die Metalle. Aufgrund der regelmäßigen Anordnung der Atome bzw. Moleküle weisen Kristalle keine kontinuierlichen, wohl aber diskrete Symmetrien auf; man spricht von Fernordnung oder Translationssymmetrie.
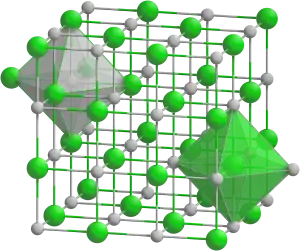
Die Wissenschaft von den Eigenschaften und Formen der Kristalle ist die Kristallographie. Eng verwandt sind die Metallographie und die Mineralogie.
Genauere Definition, Unterscheidungen
Ein Kristall ist ein homogener Körper, denn er ist stofflich und physikalisch einheitlich. Aber viele physikalische Eigenschaften sind von der Raumrichtung abhängig, d. h. ein Kristall ist anisotrop.[1]
Vor 1992 wurden Kristalle über ihre Periodizität definiert: In diesem Sinne ist ein Kristall dreidimensional periodisch aus gleichbleibenden Struktureinheiten aufgebaut.[2] Diese Struktureinheit heißt Einheitszelle oder Elementarzelle.
Seit 1992 ist ein Kristall gemäß der Internationalen Kristallographischen Union IUCr[3] durch seine diskreten Beugungsordnungen (bei Beleuchtung mit Röntgenstrahlen) definiert. Er weist also eine Fernordnung auf, ist aber nicht zwangsläufig periodisch. Diese Definition wurde durch die 1984 entdeckten Quasikristalle erzwungen, die eine Untergruppe der aperiodischen Kristalle bilden. Gleichwohl bilden die periodischen Kristalle die bei weitem größte Untergruppe der Kristalle.

Je nach Ausprägung der äußeren Form unterscheidet man
- unbeeinträchtigt ausgebildete, sogenannte idiomorphe (altgriechisch ἲδιος ìdios eigen und μορφἠ morphe Gestalt) Kristalle und
- xenomorphe (altgriechisch ξένος xénos fremd und μορφἠ morphe Gestalt) Kristalle, deren äußere Form durch fremde Grenzflächen bestimmt ist.
Der idiomorphe Kristall weist in seiner äußeren Form auf die jeweilige Kristallstruktur hin. Deshalb sind z. B. ungestört gewachsene Natriumchloridkristalle (Kochsalz, Mineral Halit) würfelförmig. Auch bei idiomorphen Kristallen liegt in der Natur meist eine gewisse Verzerrung vor, d. h. die Kantenlängen (nicht aber die Winkel) können von der Idealform deutlich abweichen (vgl. Gesetz der Winkelkonstanz).
Die äußere Form eines Kristalls wird durch die voneinander unabhängigen Merkmale Kristallhabitus und Kristalltracht bestimmt. Die Kristallflächen werden ebenso wie Gitterebenen durch Millersche Indizes beschrieben.
Kristalltypen können auch durch die Art der Bindung ihrer Bausteine unterschieden werden (z. B. Ionenkristall).
Da die charakteristische Eigenschaft von Kristallen die regelmäßige Anordnung in allen drei Raumrichtungen ist, sind auch Körper denkbar, deren Bausteine sich nur in einer oder zwei Raumrichtungen wiederholen. Dann lässt sich von eindimensionalen und zweidimensionalen Kristallen sprechen. In der Natur kommen Membranproteine vor, die sich als zweidimensionale Kristalle in der Biomembran anordnen. Ein Beispiel ist Bacteriorhodopsin.[4] In der Strukturbiologie werden 2D-Kristalle gezüchtet, um die Atompositionen der kristallisierten Makromoleküle mittels Elektronen-Kryomikroskopie zu ermitteln.[5]
.svg.png.webp)
Außer Kristallen gibt es auch Körper, die keine innere Fernordnung haben und amorph genannt werden. Ein Beispiel ist Glas (auch sogenanntes Bleikristall und anderes Kristallglas).
Wenn eine Flüssigkeit anisotrop ist und dadurch einige Eigenschaften eines Kristalls aufweist, handelt es sich um einen Flüssigkristall.[6]
Wortherkunft
Der Begriff Kristall stammt von dem griechischen Wort κρύσταλλος krýstallos (zu κρύος krýos „Eiseskälte, Frost, Eis“). Es bedeutet zunächst, bei Homer, „Eis“ – später dann auch alles dem Eis Ähnliche, Helle und Durchsichtige. Insbesondere der Bergkristall, aber auch farbige Edelsteine und Glas werden so genannt (z. B. bei Strabon und Claudius Aelianus).[7]
Bei dem bereits im antiken Griechenland betriebenen Bergbau wurden wahrscheinlich Quarz-Kristalle entdeckt. Sie wurden für Eis gehalten, das bei so tiefen Temperaturen entstanden sein müsse, dass es nicht mehr schmelzen könne. Diese Ansicht war bis ins frühe Mittelalter verbreitet. Über das lateinische crystallus (auch cristallus, vor allem „Bergkristall“,[8] und lapis cristallus[9]) hat sich die althochdeutsche Bezeichnung kristallo gebildet, die sich im Laufe der Zeit zu Kristall gewandelt hat.[10] Im 19. Jahrhundert war auch Krystall gebräuchlich.[11]
Struktur und Klassifikation periodischer Kristalle

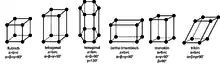
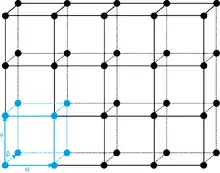

Die Richtung und die Länge der Vektoren, um die eine Kristallstruktur verschoben werden kann, so dass sich die Atompositionen wiederholen,[12] beschreiben die Translations- oder Basisvektoren. Daher wird die Struktur jeder Kristallart mit einem eigenen, spezifischen Koordinatensystem, dem Achsensystem, dargestellt.[13] Neben der Verschiebung kann eine Kristallstruktur auch gedanklich um diese Achsen gedreht werden, bis sich die gedrehte Struktur mit der ursprünglichen Struktur deckt. Weil die Translationssymmetrie erhalten bleiben muss, können nur Drehsymmetrien vorkommen, die in einer vollständigen Drehung (360°) eine, zwei, drei, vier oder sechs Wiederholungen beschreiben. Es wird dabei von 1-, 2-, 3-, 4- oder 6-zähligen Achsen gesprochen.[14] Es gibt Kristalle, die außer Drehachsen und Translationen weitere Symmetrieelemente aufweisen, nämlich Spiegelebenen und Inversionszentren, sowie Kopplungen zwischen diesen Symmetrien zu Drehinversionen[Anmerkung 1], Gleitspiegelungen[Anmerkung 2] und Schraubungen.[Anmerkung 3][15]
Für die Klassifizierung von Kristallen werden die Symmetrieeigenschaften verwendet.[16] Dabei ist die Anzahl der denkbaren Kombinations- und Kopplungsmöglichkeiten von Symmetrieelementen beschränkt (siehe auch Gruppentheorie). Es gibt bei zweidimensionalen Kristallen 17 ebene kristallographische Gruppen und bei dreidimensionalen Kristallen 230 kristallographische Raumgruppen, die vollständig in den International Tables for Crystallography, Vol. A aufgeführt sind.[17][18]
Wird ein neuer Kristall untersucht, ist die Raumgruppe zunächst unbekannt. Bei der Beschreibung der äußeren Form des Kristalls lässt er sich nur einer von 32 Punktgruppen (auch Kristallklassen genannt) zuordnen. Diese Punktgruppen beschreiben die makroskopischen Symmetrieeigenschaften der Kristalle und fassen diejenigen Raumgruppen zusammen, die sich nur in der Translationssymmetrie unterscheiden. Die Translation spielt bei der äußeren Betrachtung von Kristallen keine Rolle.[19] Weil die Winkel zwischen den Kristallflächen für jede Kristallart gleich sind und oft mit einer Rotationssymmetrie vereinbar sind (z. B. 90° bei Halit mit vierfacher Rotationssymmetrie), werden zur Beschreibung der Kristallmorphologie sieben Kristallsysteme verwendet, bei denen sich die Lage und relative Länge der Zellachsen unterscheiden. Ein Kristall ist je nach Zugehörigkeit zum entsprechenden Kristallsystem triklin, monoklin, orthorhombisch, tetragonal, trigonal, hexagonal oder kubisch.[20]
Auguste Bravais klassifizierte die verschiedenen möglichen Translationsgitter. Diese Gitter bestehen aus gleichen Parallelepipeden, deren Ecken die Gitterpunkte darstellen. Um die Symmetrie von bestimmten Gittern beschreiben zu können, ließ er neben primitiven Elementarzellen (mit einem Gitterpunkt pro Zelle) auch größere Elementarzellen zu, die flächen- oder innenzentriert sind. Ein Beispiel für eine flächenzentrierte Elementarzelle ist in Abb. 5 gezeigt. Es gibt im dreidimensionalen Raum 14 Bravais-Gitter.[11]
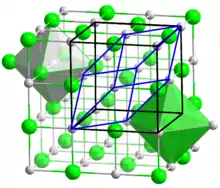
Bei der Kristallstrukturanalyse lassen sich die Streumuster der Röntgenbeugung in elf zentrosymmetrische Punktgruppen einteilen, die Lauegruppen oder Laueklassen genannt werden. Denn auch bei nicht-zentrosymmetrischen Kristallstrukturen entstehen zentrosymmetrische Beugungsmuster, da die Reflexe als Friedelpaare mit normalerweise gleicher Intensität auftreten. Die Lauegruppen lassen sich demnach herleiten, indem ein Symmetriezentrum zu der Punktgruppe des Kristalls hinzugefügt wird.[21]
Die Kristallstruktur ist nicht stoffspezifisch, das heißt eine Substanz mit bestimmter chemischer Zusammensetzung kann je nach äußeren Bedingungen (Druck, Temperatur) unterschiedliche thermodynamisch stabile Strukturen besitzen. Die verschiedenen Kristallstrukturen derselben Substanz werden Modifikationen genannt; die Existenz verschiedener Modifikationen heißt Polymorphie. Die Modifikationen stellen unterschiedliche Phasen im Sinne der physikalischen Chemie dar, deren Stabilitätsbereiche in Phasendiagrammen dargestellt werden können. Die einzelnen Modifikationen bzw. Phasen einer Substanz werden, neben eventuell vorhandenen Eigennamen, üblicherweise mit kleinen griechischen Buchstaben durchnummeriert (beim Eisen z. B. α- (Ferrit), γ- (Austenit), δ-, ε-Eisen; vgl. Eisen-Kohlenstoff-Diagramm).
Kristallisation
Ein Kristall entsteht, indem Atome oder Moleküle eine regelmäßige Struktur mit Fernordnung ausbilden. In Einstoffsystemen erfolgt die Kristallisation aus einer anderen kristallisierten Phase, aus dem Dampf oder aus der Schmelze. Außerdem können sich Kristalle aus Mehrstoffsystemen bilden, nämlich aus einer Lösung. Um die Kristallisation zu ermöglichen, darf der Zustand der Atome oder Moleküle kein Gleichgewicht sein. Bei Dampf und Lösungen wird von Übersättigung gesprochen, bei einer Schmelze von Unterkühlung.[22]
Beim Wachstum der Kristalle spielt die Geschwindigkeit eine Rolle. Bei einer Schmelze beispielsweise muss die Temperatur langsam genug unter den Schmelzpunkt sinken. Dann wird die thermische Bewegung der einzelnen Atome so gering, dass die gegenseitigen Bindungen nicht mehr durch Schwingungen aufgebrochen werden können – es kommt zur Bildung eines einheitlichen Gitters, das durch Fernordnung geprägt ist. Sinkt dagegen die Temperatur der Schmelze so schnell, dass sich die Atome nicht periodisch anordnen können, entsteht ein amorphes Material, ein Glas, das nur eine Nahordnung hat. Der Kristall hat durch seine geordnete Struktur auf einem Gitter gegenüber amorphem Glas eine geringere freie Enthalpie.
Die Bildung eines Kristalls ist ein exergonischer Prozess: Zwar nimmt die Entropie im System ab (wegen Zunahme der Fernordnung), bei Temperaturen bis zum Schmelzpunkt wird dies jedoch durch eine Enthalpieabnahme infolge Anziehung zwischen den Teilchen (= Kristallisationswärme) überkompensiert.
Ausgangspunkt für die Kristallbildung ist ein Kristallisationskeim, der bei sinkender Temperatur wächst. Existieren viele solcher Kristallkeime oder setzt die Kristallisation an mehreren Stellen gleichzeitig ein, so entsteht ein Polykristall. In vielen Fällen kommt es bei der Kristallisation zu einem Verwachsen zweier Kristalle gleicher Struktur und Zusammensetzung, aber verschiedener Orientierung im Raum (Kristallzwilling).
Umkristallisation ist die Änderung einer Kristallstruktur, bedingt durch die Änderung äußerer Faktoren wie den Druck- und Temperaturbedingungen. Hierbei wechselt der kristalline Feststoff seine Modifikation.
Die künstliche Herstellung von Kristallen bezeichnet man als Kristallzucht.
Eigenschaften
Nichtmetallische anorganische Kristalle sind härter, aber auch spröder. Alle Metalle erstarren im thermodynamischen Gleichgewicht im Regelfall kristallin.
Das Verhalten von Licht in Kristallen wird durch die Kristalloptik beschrieben. Wichtige hiermit verbundene Eigenschaften und Phänomene sind die optische Aktivität, die Polarisation, die Doppelbrechung und der Pleochroismus. Periodische dielektrische Strukturen, so genannte photonische Kristalle, zeigen neuartige optische Eigenschaften.
Manche Kristalle, z. B. Quarzkristalle, haben piezoelektrische Eigenschaften. Sie bauen eine elektrische Spannung auf, wenn sie verformt werden und verformen sich, wenn elektrische Spannung angelegt wird.[23] Dieser Effekt wird in Piezofeuerzeugen genutzt, um Zündfunken zu generieren. In der Elektronik dienen piezoelektrische Schwingquarze als Taktgeber (z. B. in Quarzuhren). Einige piezoelektrische Kristalle, jedoch nicht alle, wandeln eine Temperaturdifferenz in eine Ladungstrennung um. Diese Eigenschaft wird Pyroelektrizität genannt.[24] Solche Kristalle werden in Bewegungsmeldern und Temperaturfühlern verwendet. Ein besonderer Fall der Pyroelektrizität ist die Ferroelektrizität: Bei ferroelektrischen Kristallen kann die elektrische Polarisation durch das Anlegen einer Spannung umgepolt werden.[25]
Gitterfehler
Ein realer Kristall enthält Gitterfehler, das heißt die dreidimensional-periodische Anordnung der Atome ist gestört. Es gibt Punktfehler, Linienfehler, Flächenfehler und Volumenfehler. Punktfehler sind die einzigen Gitterfehler, die auch im thermodynamischen Gleichgewicht vorkommen. Ein Kristall ohne Gitterfehler hätte einen Zustand minimaler Entropie und ist nach dem zweiten Hauptsatz der Thermodynamik nicht zu erreichen. Im Labor gezüchtete Einkristalle haben eine Versetzungsdichte in der Größenordnung 103 - 105 cm–2, normale Kristalle und Polykristalle von 105 - 109 cm–2 und stark verformte Kristalle bis zu 1014 cm–2.[26] Für kristalloptische Eigenschaften sind meist Punkt und Volumenfehler charakteristisch, Linienfehler (Versetzungen) und Flächenfehler (Korngrenzen) hingegen für die mechanischen Eigenschaften.
Formen und Beispiele
Einkristall und Polykristall
Im Regelfall liegt ein kristalliner Festkörper als Polykristall und nicht als Einkristall vor, das heißt, er besteht aus vielen kleinen Kristallen (Kristalliten), die durch Korngrenzen voneinander getrennt sind. Zum Beispiel sind Metallgegenstände, Drähte usw. in aller Regel Polykristalle. Besteht ein Körper aus verschiedenen Kristallarten, so heißen die Grenzflächen zwischen ihnen Phasengrenzen.
Mineralien



Viele Minerale sind in der Lage, eine Vielfalt an Kristallformen und Farben auszubilden. Bekannteste Beispiele sind zum einen der Quarz, dessen Ausbildungsformen den ganzen Bereich von makrokristallin-farblos (Bergkristall) bis mikrokristallin-buntfarbig (Achat) abdeckt und zum anderen der Calcit mit ähnlichem Reichtum an Varietäten.
Die weltweit größten Kristalle wurden 2000 in der Mine von Naica entdeckt. Sie bestehen aus der Gipsart Marienglas, sind bis 14 m lang[27] und wiegen bis zu 50 Tonnen.
Der Diamant, eine kristalline Form des Kohlenstoffs, ist das härteste natürlich vorkommende Mineral. Auch Silizium kristallisiert im Diamanttyp.
Technische Anwendungen
Silizium ist zurzeit der Stoff, der am häufigsten in großen Mengen als Einkristall (Monokristall) verwendet wird, nämlich in der Halbleitertechnik. Heute üblich sind 30 cm Durchmesser des zylindrischen aus der Schmelze "gezogenen" Kristalls, ein Verfahren, das auf Jan Czochralski um 1916 zurückgeht.
Das ebenfalls als Halbleiter verwendete Galliumarsenid (GaAs) weist die so genannte Zinkblende-Struktur auf.
Die Nanotechnologie befasst sich unter anderem mit Nanokristallen.
Kleine Kristalle von Diamant, Korund, Siliziumkarbid dienen in Suspension, lose oder gebunden als Schleifmittel, einzelne Diamanten auch als Schneidewerkzeug.
Piezokristalle können Mikrophon oder Lautsprecher, Kraftsensor oder Aktuator sein.
Durch Umkristallisieren werden Präparate in Chemiefabriken gereinigt.
Nicht erwünscht ist Kristallisation jedoch bei der Herstellung von Glas. In der Metallherstellung strebt man meist möglichst feine Kristallite oder feines Korn an.
Organische Kristalle
Auch organische Stoffe, z. B. Zucker und Proteine, bilden Kristalle – letztere allerdings nur in Ausnahmefällen. Zum Beispiel befinden sich in den Peroxisomen der Pflanzen Katalase-Kristalle, die sich durch Elektronenmikroskopie sichtbar machen lassen.[28] Das Enzym Katalase ist ein Eiweiß (Protein). Die Proteinkristallographie beschäftigt sich mit der Kristallzucht aus Proteinen zur Strukturanalyse.
Kolloide
Kolloide bilden typischerweise Parakristalle, weil nicht alle Bausteine identisch sind, die Bausteine selbst typischerweise anisotrop sind und weil starke und schwache Bindungen zwischen Atomen und Atomgruppen koexistieren. Monodisperse harte-Kugel-Suspensionen können andererseits Kristalle bilden, weil die Bausteine alle identisch und isotrop sind.
Literatur
- Walter Borchardt-Ott: Kristallographie. Springer, Berlin 2002. ISBN 3-540-43964-1.
- Dorothy G. Bell: Group Theory and Crystal Lattices. In: Review of Modern Physics. Band 26, Nr. 3, 1954, S. 311.
- Charles Kittel: Einführung in die Festkörperphysik. Oldenbourg, München 2002. ISBN 3-486-27219-5.
- Will Kleber, Hans-Joachim Bautsch, Joachim Bohm: Einführung in die Kristallographie. Verlag Technik, Berlin 1998. ISBN 3-486-27319-1.
- Werner Massa: Kristallstrukturbestimmung. Teubner, Wiesbaden 2009. ISBN 978-3-8348-0649-9.
- Ulrich Müller: Anorganische Strukturchemie. Teubner, Wiesbaden 2004. ISBN 3-519-33512-3.
- Lesley Smart, Elaine Moore: Einführung in die Festkörperchemie. Vieweg, Wiesbaden 1997, ISBN 3-528-06773-X.
- Robert F. Symes und R. R. Harding: Edelsteine & Kristalle. Geheimnisvolle Schätze der Erde ; Aussehen, Entstehung, Bearbeitung, Gerstenberg Verlag, Hildesheim 1991, ISBN 3-8067-4560-9.
Weblinks
Anmerkungen
- Drehinversionen bestehen aus Drehung und Inversion; sie werden üblicherweise mit usw. gekennzeichnet.
- Gleitspiegelungen bestehen aus Translation und Spiegelung; Symbol je nach Translationsachse
- Schraubungen bestehen aus Drehung und Translation; z. B. ist das Symbol für Rotation um 180° und Translation um halben Gittervektor
Einzelnachweise
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 14.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 19.
- „Online Dictionary“ der Internationalen Kristallographischen Union (engl.).
- Hayato Yamashita, Kislon Voitchovsky, Takayuki Uchihashi, Sonia Antoranz Contera, John F. Ryan und Toshio Ando (2009): Dynamics of bacteriorhodopsin 2D crystal observed by high-speed atomic force microscopy, Journal of Structural Biology, Volume 167, Issue 2, Pages 153–158, ISSN 1047-8477, doi:10.1016/j.jsb.2009.04.011.
- Michael G. Rossmann und Eddy Arnold, Hrsg. (2001): International Tables for Crystallography Volume F: Crystallography of Biological Macromolecules. Kluwer Academic Publishers, Dordrecht u. a., Seiten 459f.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 199.
- Wilhelm Pape: Handwörterbuch der griechischen Sprache. Griechisch-deutsches Handwörterbuch. 3. Auflage. Braunschweig 1914.
- Otto Zekert (Hrsg.): Dispensatorium pro pharmacopoeis Viennensibus in Austria 1570. Hrsg. vom österreichischen Apothekerverein und der Gesellschaft für Geschichte der Pharmazie. Deutscher Apotheker-Verlag Hans Hösel, Berlin 1938, S. 140.
- Wouter S. van den Berg (Hrsg.): Eene Middelnederlandsche vertaling van het Antidotarium Nicolaï (Ms. 15624–15641, Kon. Bibl. te Brussel) met den latijnschen tekst der eerste gedrukte uitgave van het Antidotarium Nicolaï. Hrsg. von Sophie J. van den Berg, N. V. Boekhandel en Drukkerij E. J. Brill, Leiden 1917, S. 230.
- Wolfgang Pfeifer u. a.: Etymologisches Wörterbuch des Deutschen. dtv, München 1995, ISBN 3-423-03358-4, S. 735.
- Helmut G. F. Winkler: Hundert Jahre Bravais Gitter. In: Die Naturwissenschaften. Band 37, Nr. 17, 1950, S. 385–390, doi:10.1007/BF00738360.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 17.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 23.
- Siegfried Haussühl (1993): Kristallgeometrie. Weinheim Verlag. ISBN 3-527-29018-4, Seite 66.
- Werner Massa (1996): Kristallstrukturbestimmung Teubner Verlag. ISBN 3-519-13527-2, Seite 60ff.
- Siegfried Haussühl (1993): Kristallgeometrie. Weinheim Verlag. ISBN 3-527-29018-4, Seite 57.
- Theo Hahn, Hrsg. (2005): International Tables for Chrystallography, Volume A. Springer Verlag. ISBN 0-7923-6590-9.
- Zbigniew Dauter und Mariusz Jaskolski (2010): How to read (and understand) Volume A of International Tables for Crystallography: an introduction for nonspecialists. J. Appl. Cryst. (ISSN 0021-8898), 43, 1150–1171, doi:10.1107/S0021889810026956, online (PDF; 3,3 MB) abgerufen am 20. Dez. 2010.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 67.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 22.
- Theo Hahn, Hrsg. (2005): International Tables for Chrystallography, Volume A. Springer Verlag. ISBN 0-7923-6590-9, Seite 762.
- Will Kleber, Hans-Joachim Bautsch, Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 202
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, S. 267–272.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 262.
- Will Kleber, Hans-Joachim Bautsch und Joachim Bohm (1990): Einführung in die Kristallographie. Verlag Technik. ISBN 3-341-00479-3, Seite 264.
- H. Föll et al.: Einführung in die Materialwissenschaft I. TF der CAU Kiel, abgerufen am 23. Oktober 2020.
- GEO Magazin Nr. 05/08. Höhlenforschung: In der Kammer der Kristallriesen, S. 2 von 4.
- Elmar Weiler und Lutz Nover (2008): Allgemeine und molekulare Botanik. Georg Thieme Verlag, Stuttgart und New York. ISBN 978-3-13-147661-6, Seite 73, Abb. 2.21 und Seite 327, Abb. 10.8.