Schwingquarz
Ein Schwingquarz, häufig vereinfachend abgekürzt als Quarz bezeichnet, ist ein elektronisches Bauelement in Quarzoszillatoren, welches zur Erzeugung von elektrischen Schwingungen mit einer bestimmten Frequenz dient. Seine Funktionsweise basiert dabei auf dem Prinzip der elektromechanischen Resonanz des verbauten piezoelektrischen und mit Elektroden versehenen Quarzkristalls. Ein in der Funktion ähnliches elektronisches Bauelement – aber mit anderem Werkstoff – stellt der Keramikresonator dar.
Historisches
Erste systematische und wissenschaftlich dokumentierte Versuche mit elektromechanischen Resonanzschwingungen führte Alexander M. Nicholson 1918 mit natürlich gewachsenen Seignettesalzkristallen durch.[1] Bereits ein Jahr später ersetzte Walter Guyton Cady den Seignettesalzkristall durch den effizienteren und auch heute noch gebräuchlichen Quarzkristall.
Die Bell Telephone Laboratories und andere Forschungseinrichtungen trieben ab 1923 die Entwicklung von praxistauglichen Schwingquarzen[2] hauptsächlich zur Frequenzstabilisierung in der Funktechnik voran und bewarben deren Einsatz in diversen zeitgenössischen Publikationen.[3]
1928 entwickelte Warren Marrison, ein Mitarbeiter der Bell Telephone Laboratories, die erste quarzgesteuerte Uhr, die die Genauigkeit der Zeitmessung enorm erhöhte.[4]
Ab 1934 konnten weniger temperaturabhängige Schwingquarze zur Frequenzstabilisierung mithilfe verfeinerter Kristallbearbeitungsverfahren (sogenannte Schnitte) hergestellt werden. Die hohe Feuchte-Empfindlichkeit und damit einhergehende unerwünschte Schwankungen der Resonanzfrequenz ließen sich jedoch erst Anfang der 1950er Jahre durch die Verwendung geschlossener Metall- oder Glasgehäuse deutlich verringern.
Während des Zweiten Weltkrieges führte der vermehrte Einsatz von militärischer Funktechnik zu einer erhöhten Nachfrage nach Schwingquarzen, die durch natürliche Quarzkristalle allein nicht mehr gedeckt werden konnte und die Entwicklung von Verfahren zur Herstellung synthetischer Kristalle zur Folge hatte. Bereits 1948 erfolgte die Quarzsynthese in industriellem Maßstab. Weitere erwähnenswerte Verfeinerungen, insbesondere im Hinblick auf die Miniaturisierung der hergestellten Kristalle, wurden erst 1968 durch J. Staudte erzielt.
Ab den 1950er Jahren ist durch die Einbeziehung sogenannter Oberschwingungen des Kristalls der steuerbare Frequenzbereich und damit auch der Einsatzbereich der Schwingungsquarze stark erweitert worden. Seitdem konzentriert sich die Entwicklung auf eine Reduzierung von Störeinflüssen, d. h. auf die Erhöhung der Güte.
Allgemeines zum Aufbau und zur Funktion
Der Quarzkristall wird beidseitig mit Elektroden versehen, an die ein von einem beliebigen Oszillator erzeugtes Wechselfeld angelegt wird. Durch Rückkopplung wird die Frequenz des Wechselfeldes mit der mechanischen Eigenfrequenz des Quarzkristalls in Übereinstimmung gebracht. Dadurch wirkt der Schwingquarz wie ein elektrischer Resonanzkreis mit sehr geringer Dämpfung (= sehr hohem Gütefaktor). Oszillatoren mit Schwingquarzen können, wenn sie entsprechend eingesetzt werden, Frequenzgenauigkeiten erreichen, die weit über die meisten Anforderungen der Industrie hinausgehen.
Der Schwingquarz führt im elektrischen Wechselfeld Deformationsschwingungen (Längs-, Dickenscher- oder Biegeschwingungen) aus, wenn die Frequenz des Wechselfeldes mit der Eigenfrequenz des Quarzplättchens übereinstimmt.
Ein Quarz kann in Serien- oder Parallelresonanz betrieben werden. Die beiden Eigenfrequenzen liegen sehr eng beieinander. Die Resonanzfrequenz lässt sich geringfügig auch durch die äußere Beschaltung beeinflussen. Häufig wird dazu ein Trimmer mit wenigen pF in Serie oder parallel zum Quarz geschaltet (abhängig davon, ob der Quarz in Serien- oder Parallelresonanz betrieben wird), um Herstellungstoleranzen ausgleichen zu können („Ziehen“ des Quarzes). Die elektrische Schaltung dieser speziellen Oszillatoren nennt sich Quarzoszillator.
Die Eigenfrequenzen des Quarzes sind in geringem Maße von der Temperatur abhängig. Der Temperaturkoeffizient lässt sich jedoch durch Wahl des Quarzschnitts (Geometrie in Bezug auf die Kristallachsen) beeinflussen, so dass er für die Verwendung als Zeitbasis sehr gering gehalten werden kann. Um Frequenzänderungen besonders gering zu halten, kann der Schwingquarz auch durch einen Quarzofen thermostatiert werden.
Grundlagen
Eigenschaften des Quarzkristalls
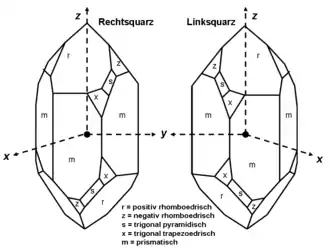
Das Basismaterial eines Schwingquarzes ist einkristalliner Quarz bzw. Siliziumdioxid (SiO2), das auch natürlicherweise als Bergkristall vorkommt. Die ersten Schwingquarze wurden tatsächlich aus Bergkristall gefertigt, während man heute künstliche Kristalle verwendet. Quarz kristallisiert im trigonalen Kristallsystem trigonal-trapezoedrisch (α-Modifikation) und tritt daher als „Rechts-“ oder als „Linksquarz“ auf.[5][6][7]
Die beiden Arten sind sich spiegelbildlich gleich. Der Querschnitt eines idealen Quarzkristalls ist sechseckig. Wie in der Kristallographie üblich, werden die drei senkrecht aufeinander stehenden Achsen mit x, y und z definiert. Die z-Achse, auch optische Achse genannt, geht durch die Spitze des Kristalls. Die y-Achse verbindet zwei sich gegenüber liegende Seitenflächen des Kristalls miteinander und wird mechanische Achse genannt. Die x-Achse ist die sogenannte elektrische Achse, weil bei mechanischer Belastung des Kristalls in dieser Richtung eine elektrische Ladung auftritt, d. h., es wird Piezoelektrizität beobachtet. Oberhalb von 573 °C werden Quarzkristalle hexagonal und sind frei von piezoelektrischen Effekten.
Aus dem Quarzkristall wird ein Schwingquarz, indem aus dem Kristall eine Scheibe oder ein quaderförmiges Plättchen in einer genau definierten kristallographischen Orientierung (Quarzschnitt) herausgeschnitten wird. Wird diese Scheibe oder das Plättchen mechanisch deformiert, so werden elektrische Ladungen auf seiner Oberfläche erzeugt. Dieser piezoelektrische Effekt ist umkehrbar, das heißt, wird ein elektrisches Feld an das Material gelegt, so verformt es sich (inverser Piezoeffekt). Sobald das elektrische Feld nicht mehr anliegt, nimmt das Material seine ursprüngliche Form wieder an. Eine dabei angeregte (gedämpfte mechanische) Schwingung resultiert in einer entsprechenden elektrischen Spannung. Mit dem Prinzip der Rückkopplung kann dieses Signal für die Aufrechterhaltung der mechanischen Resonanzschwingung des Materials genutzt werden. Durch die Aufhängung, saubere Oberflächen und geeignete Schwingungsmodi wird sehr geringe Dämpfung und außerordentlich hohe mechanische Stabilität und bei geeignetem Schnitt auch geringe Temperaturabhängigkeit erreicht. Solche Quarzoszillatoren liefern Taktsignale mit sehr stabiler Frequenz. Je nach jeweils erregtem mechanischem Schwingungsmodus und der Dimension des Plättchens überdecken Schwingquarze unterschiedliche Frequenzbereiche. Es können auch Oberwellen erregt werden.
Schwingungsformen
- Schwingungsmodi bei Kristallen für Schwingquarze
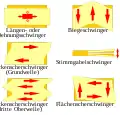Schwingungsmodi von Quarzkristallen[8]
Deformations-
schwingungen eines Dickenscherschwingers
Ein aus einem Quarzkristall herausgeschnittenes Quarzplättchen führt im elektrischen Wechselfeld Deformationsschwingungen aus, wenn die Frequenz des Wechselfeldes mit der Eigenfrequenz des Quarzplättchens übereinstimmt. Die Resonanzfrequenz wird durch die Materialkonstanten und die mechanischen Abmessungen bestimmt. Die Deformationsschwingungen von Quarzresonatoren können in unterschiedlichen mechanischen Schwingungsformen auftreten.
Längen- und Biegeschwinger werden zur Erzeugung von kleineren Frequenzen unterhalb 1 MHz eingesetzt:
Längenschwinger, auch Dehnungsschwinger genannt, sind plattenförmige Resonatoren, die in Richtung ihrer längeren Abmessung schwingen. Die Längenänderung wird durch ein elektrisches Wechselfeld, das senkrecht zur Schwingrichtung anliegt, hervorgerufen. Die Schwingung ist eine stehende akustische Welle, die einen oder mehrere Schwingungsknoten zwischen den Enden hat. Die Resonatorlänge ist ein ganzes Vielfaches der halben Wellenlänge.
Biegeschwingungen in den Biegeschwingern können angeregt werden, indem Längenschwinger mit zwei gegenphasig angeschlossenen Elektroden versehen werden, so dass zwei entgegengesetzte Felder in x-Richtung auftreten. Hierdurch wird eine Biegung in z-Richtung erzwungen. Die Frequenzkonstante der meist quadratischen Kristallstäbe von Biegeschwingern wird von den Materialkonstanten und der Länge l und der Breite b des Resonators bestimmt, sodass für Biegeschwinger kein einheitlicher Zahlenwert angegeben werden kann.
Eine Sonderform der Biegeschwinger sind die Stimmgabelschwinger (Stimmgabelquarz). Sie können mit dem Bild eines gebogenen Stabes erklärt werden, der Biegeschwingungen ausführt. Die Frequenz von Stimmgabelschwingern ist von der Zinkenlänge und Breite abhängig. Stimmgabelschwinger werden überwiegend zur Erzeugung von sehr geringen Frequenzen für Quarzuhren eingesetzt. Typisch hierfür sind 32,768 kHz (215 Hz), siehe auch Uhrenquarz.
Die Schwingungen in Dickenscherschwingern ergeben sich aus gegenläufigen Verschiebungen zweier größerer Oberflächenbereiche gegeneinander. Der oder – bei Oberwellenquarzen – die Schwingungsknoten befinden sich innerhalb des Resonators. Bei einem bestimmten Verhältnis des Resonatordurchmessers zur Dicke des Kristalls sowie zur Größe der Elektroden treten am Resonatorumfang keine mechanischen Schwingungen auf, die Halterung des Kristalls ist problemlos möglich und die eventuell nicht ideale Oberfläche liefert keine Beiträge zur Ungenauigkeit.[9] Dickenscherungsschwinger sind aufgrund der Resonanzart daher besonders robust gegenüber äußeren Einflüssen. Sie werden in der Schnittform des AT-Schnittes am häufigsten in Schwingquarzen eingesetzt und kommen praktisch für alle Frequenzen ab 1 MHz aufwärts zur Anwendung. Bis etwa 20 bis 30 MHz werden die Resonatoren in ihrer Grundwelle betrieben. Oberhalb 30 MHz bis etwa 250 MHz werden Dickenscherschwinger mit ihrer ungeraden Oberwelle bis hin zur 9. Oberwelle angeregt.
Die Resonanzschwingung in Flächenscherschwingern ergibt sich aus gegenläufigen Verschiebungen von je zwei Seitenflächenbereichen gegeneinander. Die Resonanzfrequenz der Flächenscherschwinger wird durch die Abmessungen der Kantenlängen der meist quadratischen oder rechteckigen Resonatoren und den richtungsabhängigen elastischen Werten des Kristalls bestimmt. Hieraus resultieren vom Kristallschnitt abhängige Frequenzkonstanten N mit bevorzugten Frequenzbereichen.
Kristallschnitte
Die Eigenschaften von Schwingquarzen wie die thermische Stabilität der Resonanzfrequenz, die internen Verluste und die Ziehbarkeit (Trimmbarkeit durch externe Beschaltung) werden vom Schnittwinkel bestimmt, mit dem die Resonatorplättchen aus dem Quarzkristall herausgeschnitten werden. Durch den Schnittwinkel ist die Richtung der Kristallisation in einem Resonatorplättchen vorgegeben, womit die mechanischen Eigenschaften des Piezokristalls beeinflusst werden. Dies gilt auch für weitere Bauelemente wie z. B. Oberflächenwellenfilter (englisch surface acoustic wave, SAW), die mit Quarzkristallen als Basismaterial arbeiten.
- Lage verschiedener Kristallschnitte im Quarzkristall
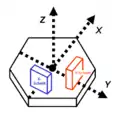Lage der Koordinaten im Quarzkristall mit Darstellung der Lage des X- und des Y-Schnittes
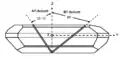Lage des AT- und des BT-Schnittes im Quarzkristall[10]
Schnittwinkel verschiedener Kristallschnitte von Schwingquarzen
Die Lage der Schnitte im Quarzkristall wird mit Hilfe der geometrischen Achsen als Winkel zwischen X und Y und ggf. auch noch Z definiert. Jeder spezielle Schnitt wird mit einer Buchstabenkombination gekennzeichnet, wobei ein „T“ in dieser Kombination immer auf einen Temperatur-stabilisierten Schwingquarz hinweist.[11]
- Temperaturbedingte Frequenzänderungen bei Schwingquarzen mit unterschiedlichen Kristallschnitten
Frequenzänderungen in Abhängigkeit von der Temperatur bei verschiedenen Kristallschnitten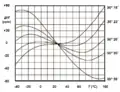
Frequenzänderungen in Abhängigkeit von der Temperatur beim AT-Schnitt mit leicht geänderten Schnittwinkeln
Hauptunterscheidungsmerkmal der verschiedenen Kristallschnitte ist die unterschiedliche Abhängigkeit der Resonanzfrequenz von der Temperatur. Dazu sind im linken oberen Bild die Frequenzänderungen im Temperaturbereich von −40 °C bis +120 °C bei verschiedenen Kristallschnitten aufgeführt. Es zeigt sich, dass die Kristallschnitte, bis auf den AT-Schnitt, die Kurvenform einer nach unten offenen Parabel aufweisen. Im Scheitelpunkt der Parabel besteht ein mehr oder weniger großer Temperaturbereich, in dem die Frequenzänderung verhältnismäßig gering ist. Der AT-Schnitt bildet dagegen einen sinus- oder S-förmigen Kurvenverlauf der Frequenzänderung über die Temperatur. Er kann so gelegt werden, dass der Kurvenverlauf am Wendepunkt der Sinuskurve den Temperaturbereich von −40 °C bis +100 °C in der Weise abdeckt, dass die Frequenzänderung Δf/f kleiner ± 30 ppm wird, wobei der Bereich am Wendepunkt bei etwa 25 bis 35 °C liegt und dort im Idealfall so gut wie keine Frequenzänderung eintritt. Deshalb werden mehr als 90 % aller gefertigten Schwingquarze, mit Ausnahme der Stimmgabelquarze, mit Kristallen im AT-Schnitt hergestellt.[12]
Der Standard-AT-Schnitt hat für Frequenzen bis 10 MHz einen Steigungswinkel des Kristallschnittes von 35°15’ der X-Achse gegenüber der optischen Z-Achse auf (35°18’ für Frequenzen > 10 MHz). Wie das rechte obige Bild zeigt, kann mit einer geringen Änderung des Schnittwinkels der Kurvenverlauf deutlich beeinflusst werden. Damit kann der obere Wendepunkt der Frequenz-Änderungskurve in den höheren Temperaturbereich gelegt werden. Durch Aufheizen des Schwingquarzes kann der Arbeitspunkt in diesen Bereich gelegt werden, so dass die erzeugte Frequenz unabhängig von der Umgebungstemperatur wird. Dies wird bei den temperaturkompensierten Oszillatoren TCXO und OCXO ausgenutzt.
Die Frequenz eines Quarzkristalls in der Grundwelle hängt linear im umgekehrten Verhältnis von der Dicke des Plättchens ab. Das bedeutet, dass der mechanisch dünnste herstellbare Kristallschnitt die höchste Resonanzfrequenz bestimmt. Dieser Grenzwert liegt heutzutage (2010) bei etwa 50 µm. Die Frequenzkonstante, das ist die Dicke eines Plättchens, die eine Resonanzfrequenz von 1 MHz zur Folge hat, beträgt beispielsweise für AT-Schnitte 1,661 mm. Das heißt, dass mit einer Dicke des Quarzplättchens von 50 µm eine Resonanzfrequenz von etwa 30 MHz erzeugt werden kann. Allerdings kann durch Strukturätzen des geschnittenen Kristalls mit der Inverted-Mesa-Technik die Dicke eines Quarzplättchens noch bis auf etwa 30 µm verringert werden, so dass mit dieser speziellen Herstelltechnik eine obere Resonanzfrequenz der Grundwelle von 55,7 MHz erreicht werden kann.[8]
Neben der Dicke eines Resonators sind die äußeren Abmessungen des Quarzplättchens bzw. der Quarzscheibe eine wichtige Größe. Sie bestimmen die Güte des Schwingquarzes, je größer die Abmessungen des Resonators sind, desto höher ist der Gütefaktor.[8]
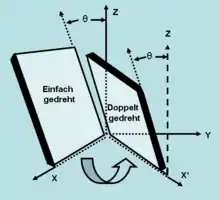
Neben den einfach gedrehten Schnitten durch den Kristall werden auch Schnitte durchgeführt, die doppelt gegenüber der X-Achse gedreht sind. Schnitte dieser Art sind oft für Sensoren bestimmt.
| Schnitt | Frequenzbereich | Schwingungsmodus | Schnittwinkel | Hinweise |
|---|---|---|---|---|
| AT | 0,5–30 MHz (Grundton) 15…75 MHz (3. Oberton) 50…150 MHz (5. Oberton) 100…200 MHz (7. Oberton) 150…300 MHz (9. Oberton) |
Dickenscherschwinger | 35°15′, 0° (< 25 MHz) 35°18′, 0° (>10 MHz) |
Vorteil des AT-Schnittes ist ein geringer und nahezu linearer Temperaturgang der Resonanzfrequenz bei etwa 25…35 °C. Durch geringe Änderungen des Schnittwinkels können AT-Resonatoren mit nahezu linearer Temperaturabhängigkeit der Frequenz bei höheren Temperaturen für temperaturkompensierte Oszillatoren (TCXO, OCXO) hergestellt werden.[14]
AT-Quarze sind empfindlich gegenüber mechanischen Belastungen, verursacht durch Vibration oder Stoß oder Temperaturwechsel. |
| SC | 0,5…200 MHz | Dickenscherschwinger | 35°15′, 21°54′ Doppelt gedreht |
SC-Schnitt (SC = stress compensated)
Vorteile des SC-Schnittes sind geringes Phasenrauschen und geringe Alterung. Der Frequenzgang ist bei 95 °C nahezu linear. SC-Resonatoren sind gegenüber AT-Resonatoren weniger empfindlich gegenüber mechanischen Belastungen, verursacht durch Vibration, Stoß oder Temperaturwechsel, haben im Vakuumbetrieb eine höhere Güte und sind weniger empfindlich gegenüber der Einwirkung der Schwerkraft. Sie werden in der Raumfahrt und in GPS-Systemen in temperaturkompensierten Oszillatoren (TCXO, OCXO) eingesetzt.[15] |
| BT | 0,5…200 MHz | Dickenscherschwinger | −49°8′, 21°54’ | Der BT-Schnitt hat bei 25 °C ähnliche Eigenschaften wie der AT-Schnitt.
Wegen der gegenüber den AT- und SC-Schnitten dickeren Kristallplättchen können im BT-Schnitt Resonatoren für Frequenzen über 50 MHz im Grundton hergestellt werden.[16] |
| IT | Dickenscherschwinger | Doppelt gedreht | Der IT-Schnitt hat ähnliche Eigenschaften wie der SC-Schnitt.
Der Frequenzgang bei 78 °C ist nahezu linear. IT-Resonatoren werden in temperaturkompensierten Oszillatoren (TCXO, OCXO) eingesetzt. | |
| FC | Dickenscherschwinger | Doppelt gedreht | Der FC-Schnitt hat ähnliche Eigenschaften wie der SC-Schnitt.
Der Frequenzgang ist bei 52 °C nahezu linear. Weil diese Temperatur niedriger ist als bei SC- und IT-Schnitten, gilt der FC-Schnitt als Energie sparende Version für temperaturkompensierte Oszillatoren (TCXO, OCXO).[17] | |
| AK | Dickenscherschwinger | Doppelt gedreht | Der AK-Schnitt hat ein besseres Temperatur-Frequenzverhalten als AT- und BT-Schnitte mit einer höheren Toleranz gegenüber der Kristall-Orientation als die AT-, BT- und SC-Schnitte.[18] | |
| CT | 300…900 kHz | Flächenscherschwinger | 38°, 0° | Die Parabelöffnungskonstante a zwischen 0 und +90 °C liegt bei etwa −0,05…−0,06 ppm/K².[6]
Quarzkristalle im CT-Schnitt werden meist für niedrige Frequenzen im kHz-Bereich verwendet, am häufigsten für Uhrenquarze und Funkuhrenquarze. |
| DT | 75…800 kHz | Flächenscherschwinger | −52°, 0° | Die Parabelöffnungskonstante a zwischen −1 und +60 °C liegt bei etwa −0,02 ppm/K².[6] |
| SL | 400…800 kHz | Flächenscherschwinger | −57°, 0° | Die Parabelöffnungskonstante a zwischen −1 und +80 °C liegt bei etwa −0,04 ppm/K².[6] |
| GT | 0,1…3 MHz | Längenschwinger | 51°7′ | Die Parabelöffnungskonstante a zwischen −25 und +75 °C ist nahezu Null. |
| E, 5°X | 50…250 kHz | Längenschwinger | Der E-Schnitt hat einen sehr geringen Temperaturkoeffizienten. Er wird für Quarzfilter im niedrigen Frequenzbereich eingesetzt. | |
| MT | 40…200 kHz | |||
| ET | 66°30′ | |||
| FT | −57° | |||
| NT | 8…130 kHz | Biegeschwinger | Die Parabelöffnungskonstante zwischen 10 und 50 °C liegt bei etwa −0,05 ppm/K².[6] | |
| XY, | 3…85 kHz | Biegeschwinger, Stimmgabel- schwinger |
Der XY-Schnitt ist der am meisten verwendete Niederfrequenz-Schwingquarzschnitt. Er ist kleiner als andere Niederfrequenzschnitte, preiswerter herzustellen, hat eine niedrige Impedanz und ein geringes Co/C1-Verhältnis. Die Haupt-Applikation ist die Uhrenfrequenz 32,768 kHz. Die Parabelöffnungskonstante a zwischen 10 und 50 °C liegt bei etwa 0,04 ppm/K².[6] | |
| H | 8…130 kHz | Biegeschwinger | Der H-Schnitt wird für Breitbandfilter verwendet. Er hat einen linearen Temperaturkoeffizienten.[19] | |
| J | 1…12 kHz | Längen- Biegeschwinger |
Der J-Schnitt besteht aus einer Zusammenschaltung zweier Quarzplättchen zu einem Resonator. Die einzelnen Resonatoren werden so ausgewählt, dass die beiden Resonatoren bei einem gegebenen elektrischen Feld unterschiedliche Resonanzfrequenzen ausweisen. Dadurch entsteht eine sehr niederfrequente überlagerte Resonanz.[19] | |
| RT | Doppelt gedreht | — | ||
| SBTC | Doppelt gedreht | — | ||
| TS | Doppelt gedreht | — | ||
| X 30° | Doppelt gedreht | — | ||
| LC | Dickenscherschwinger | 11,17°/9,39° Doppelt gedreht |
Der LC-Schnitt (LC = Linear Coeffizient) besitzt einen linearen Temperaturkoeffizienten. Er kann als Sensor in Quarz-Thermometern verwendet werden.[20] | |
| AC | 31° | Der AC-Schnitt (Coupling = 0) zeichnet sich durch geringe Verkopplung zu anderen Schwingungsmodi aus und ist frei von Unstetigkeiten im Temperaturgang der Frequenz. Er kann als Sensor in Quarz-Thermometern verwendet werden. Der Temperaturkoeffizient beträgt 20 ppm/K.[9][21] | ||
| BC | −60° | Der BC-Schnitt kann als Sensor in Quarz-Thermometern verwendet werden. | ||
| NLSC | Der NLSC-Schnitt kann als Sensor in Quarz-Thermometern verwendet werden. Der Temperaturkoeffizient beträgt 14 ppm/K.[21] | |||
| Y | Der Y-Schnitt kann als Sensor in Quarz-Thermometern verwendet werden. Der Temperaturkoeffizient beträgt 90 ppm/K.[22][21] | |||
| X | 10…100 kHz 40…200 kHz |
Biegeschwinger, Dehnungs- schwinger |
0 0 |
Der X-Schnitt wurde im ersten Ultraschall-Quarzoszillator 1921 von W. G. Cady und im ersten 50-kHz-Oszillator für Uhren 1927 von Horton und Marrison verwendet.[23][24] Die Parabelöffnungskonstante a zwischen 0 und 45 °C liegt bei 0,04 ppm/K².[6] |
Frequenzkonstante
Die Deformationsschwingungen, die ein Quarzkristall bei Resonanz im elektrischen Wechselfeld ausführt, wenn die Frequenz f des Wechselfeldes mit der Eigenfrequenz des Quarzplättchens übereinstimmt, wird, wie bei allen mechanischen Schwingern, durch die Materialkonstanten und durch die mechanischen Abmessungen bestimmt.
mit und , worin die Abmessung in Schwingungsrichtung, ρ die Dichte und den Elastizitätsmodul bedeutet.
Der Ausdruck
wird allgemein Frequenzkonstante oder auch Schwingungskoeffizient genannt und ist, wegen der Richtungsabhängigkeit des Elastizitätsmoduls, von der Schnittorientierung abhängig. Jeder Quarzschnitt hat eine bestimmte Frequenzkonstante, die maßgebend für die Länge des Resonators in Schwingungsrichtung ist, oder anders ausgedrückt, die Frequenz eines Quarzkristalls in der Grundwelle hängt linear im umgekehrten Verhältnis von der Dicke des Plättchens ab. Das bedeutet, dass der mechanisch dünnste herstellbare Kristallschnitt die höchste Resonanzfrequenz bestimmt. Dieser Grenzwert liegt heutzutage (2010) bei etwa 50 µm.
Bei der Frequenzkonstante von 1661 kHz · mm beispielsweise für AT-Schnitte ergibt sich daraus, dass mit einer Dicke des Quarzplättchens von 50 µm eine Resonanzfrequenz von etwa 30 MHz erzeugt werden kann. Allerdings kann durch Strukturätzen des geschnittenen Kristalls mit der Inverted-Mesa-Technik die Dicke eines Quarzplättchens noch bis auf etwa 30 µm verringert werden, so dass mit dieser speziellen Herstelltechnik eine obere Resonanzfrequenz der Grundwelle von 55,7 MHz bei AT-Quarzen erreicht werden kann. Eine Übersicht über die Frequenzkonstanten verschiedener Quarzschnitte gibt die folgende Tabelle:
| Schwingungsform |
Frequenzkonstante N = f · l[6][19] |
Frequenzbereich |
|---|---|---|
| Dickenscherschwinger, AT-Schnitt | 1661 kHz · mm | — |
| Dickenscherschwinger, SC-Schnitt | 1797 kHz · mm | — |
| Dickenscherschwinger, BT-Schnitt | 2536 kHz · mm | — |
| Längenschwinger, GT-Schnitt | 2808 kHz · mm | — |
| Flächenscherschwinger, DT-Schnitt | 2070 kHz · mm | 180 bis 350 kHz |
| Flächenscherschwinger, CT-Schnitt | 3070 kHz · mm | 300 bis 1000 kHz |
| Flächenscherschwinger, SL-Schnitt | 4600 kHz · mm | 400 bis 800 kHz |
Herstellung
Die Herstellung von Schwingquarzen erfolgt in mehreren nachfolgend beschriebenen Schritten, die zusammengefasst werden können in:
- Synthetische Herstellung des Quarzkristalls
- Herstellen der Blanks
- Kontaktieren und Montage
Synthetische Herstellung des Quarzkristalls
etwa 190 mm lang und 127 g schwer
Ursprünglich wurden Schwingquarze aus natürlich vorkommenden Quarzkristallen, auch Bergkristall genannt, hergestellt. Aber das natürliche Material bildet oft keinen idealen Kristall. Es treten Verzwilligungen (Zwillingskristalle) auf, das sind Verwachsungen innerhalb des Kristalls, deren Hauptachsen nicht übereinstimmen. Weiterhin können solche Kristalle Wachstumsunterbrechungen, Gas- und Flüssigkeitseinschlüsse aufweisen, so dass in der Industrie mit den natürlich vorkommenden Kristallen eine Großserienfertigung nicht möglich ist. Die zur Herstellung von Schwingquarzen benötigten Kristalle werden deshalb schon seit den 1950er Jahren nach dem Hydrothermal-Prinzip synthetisch hergestellt. Hierbei wird die geologische Entstehung von Quarz in vertikalen Autoklaven nachgebildet.
Der Autoklav ist im unteren Bereich mit einer Natriumhydroxid-Lösung gefüllt, in der sich feinverteilter Naturquarz bei etwa 400 °C und 800 bar unter Kieselsäurebildung bis zur Sättigung auflöst. Durch Wärmekonvektion strömt die übersättigte Lösung in den oberen Teil des Autoklaven und kristallisiert dort bei einer Temperatur von etwa 400 °C und 1000–1500 bar[25][9] an dort befindlichen Quarz-Impfkristallen (engl. seed) aus. Die abgekühlte Lösung sinkt wieder in den heißeren Bereich ab und nimmt erneut Kieselsäure auf. Es entsteht ein Kreislauf, der zum Wachsen von Quarz-Einkristallen mit einer Wachstumsrate von etwa 0,2 bis 1 Millimeter pro Tag führt.[8] Die Kristallbildung erfolgt überwiegend auf der Z-Fläche und ist frei von Verwachsungen und Verzwilligungen. Im Allgemeinen dauert der Wachstumsprozess etwa 40 bis 80 Tage und ergibt Einkristalle von etwa 200 mm Länge und einer Breite von bis zu 50 mm mit einem Gewicht von etwa 0,2 bis 1 kg. Die Weltjahresproduktion geht mittlerweile in die Millionen Tonnen.[26]
Die synthetische Herstellung des Quarz-Einkristalls hat weitere Vorteile. Da die Zusammensetzung des Grundmaterials sehr genau bestimmt werden kann, kann die Reinheit des Kristalls, die entscheidend für die spätere Güte und die zeitliche Frequenzstabilität des Schwingquarzes ist, recht genau eingestellt werden. Zusatzstoffe, die ggf. die Wachstumsgeschwindigkeit erhöhen und deren Auswirkungen auf das Verhalten der Quarze bekannt sind, können somit präzise beigemischt werden.
Herstellen der Blanks
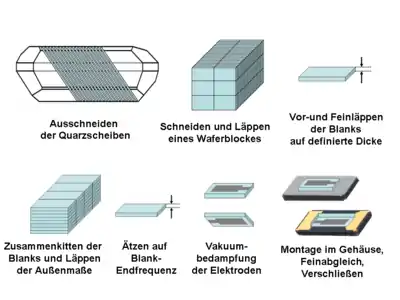
Die eigentliche Fertigung eines Schwingquarzes beginnt mit dem Herausschneiden eines Plättchens (Wafers) aus dem Quarzkristall in dem vorgesehenen Schnittwinkel. Zum Schneiden kommen Kreis- oder Bandsägen zum Einsatz. Die Messung der Schnittwinkel erfolgt über eine hochpräzise Röntgen-Messmethode.[27][28] Mit dieser Methode kann der Schnittwinkel auf etwa eine Winkelminute genau eingestellt werden. Die herausgeschnittenen Plättchen werden „Wafer“ genannt. Sie haben zunächst noch nicht die Abmessungen des späteren Resonators. Dazu werden sie erst einmal zu einem Block zusammengefügt und dann so zurechtgeschnitten, dass durch Trennen die Abmessungen der späteren Quarzresonatoren, „Quarzblanks“ oder kurz „Blanks“ genannt, entstehen.
Nachdem der Waferblock an den zugänglichen Seitenflächen geschliffen und geläppt wurden, wird er anschließend in die gewünschte Größe der Blanks zersägt. Die einzelnen Blanks werden dann in mehreren Schritten auf die gewünschte Dicke geläppt. Hohe Präzisionsanforderungen bestehen dabei hinsichtlich möglichst geringer Oberflächen-Unebenheiten sowie einer genauen Plan-Parallelität der Oberflächen zueinander. Durch Zusammenfügen der Blanks zu einem Block können danach die äußeren Abmessungen der Blanks mit großer Gleichmäßigkeit in einer Großserie in Übereinstimmung gebracht werden.
Nach dem erneuten Trennen der Blanks voneinander werden dann die Resonatorplättchen mit Ätzverfahren auf eine etwas geringere Dicke gebracht, als es die gewünschte Frequenz des Schwingquarzes eigentlich erfordert. Denn durch die danach erfolgende metallische Beschichtung der Blanks, dem Aufbringen der Elektroden, kann die Resonanzfrequenz des Plättchens im Nachhinein noch beeinflusst werden.
Nachdem jetzt die Blanks die gewünschte Dicke besitzen, erfolgt je nach Größe und vorgesehener Frequenz eine Weiterbearbeitung. Für größere Bauformen werden die Blanks gerundet und die Scheiben ggf. mit einer Facette versehen. Kleinere Bauformen, insbesondere die für SMD-Quarze, bleiben in einer rechteckigen Form.
Kontaktieren und Montage
Es versteht sich von selbst, dass für Schwingquarze, die eine möglichst hohe Güte und Frequenzstabilität aufweisen müssen, hohe Anforderungen an die Reinheit, Sauberkeit und die Präzision der nachfolgenden Prozesse gestellt werden und in der Serienproduktion auch gewährleistet werden müssen. Sind die Quarzblanks in ihre mechanisch endgültige Form gebracht, werden sie zunächst kontaktiert. Dies erfolgt in Vakuumkammern durch Aufdampfen von metallischen Elektroden, meist Silber, auf die Oberflächen der Blanks. Durch gleichzeitiges Messen der individuellen Resonanzfrequenz kann beim Aufdampfen der Elektroden die Schichtdicke noch leicht variiert werden, so dass hiermit eine Feinabstimmung der gewünschten Resonanzfrequenz durchgeführt werden kann.
Die metallisierten Resonatoren werden anschließend mit einer geeigneten Halterung elektrisch mit Anschlüssen, die nach außen geführt werden können, verbunden. Bei scheibenförmigen Resonatoren sind dies oft Federhalterungen, bei SMD-Schwingquarzen, aber auch bei liegend eingebauten Resonatoren erfolgt die Kontaktierung meist über eine Bondung.[29]
Es folgt eine Lagerung des Resonators bei einer höheren Temperatur (200 °C),[28] die eine Voralterung (engl. aging) des Quarzes bewirkt. Der kontaktierte und vorgealterte Resonator wird dann anschließend in einem evakuierten oder mit Stickstoff (N2) gefüllten hermetisch dichten Gehäuse eingebaut, um Umwelteinflüsse und Oxidation durch Luftsauerstoff gering zu halten, somit günstiges Alterungsverhalten und langlebigen Einsatz bei hoher Stabilität zu gewährleisten. Endgemessen und beschriftet, sofern Platz genug auf dem Gehäuse zur Verfügung steht, kann er dann als Schwingquarz seine Funktion in elektronischen Geräten erfüllen.
Ersatzschaltung und elektrisches Verhalten
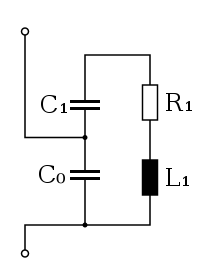
Das elektrische Verhalten eines Schwingquarzes in der Nähe seiner Resonanzfrequenz entspricht einer Parallelschaltung, bestehend aus einem verlustbehafteten Serienresonanzkreis und einer statischen Parallelkapazität C0, die sich aus der Kapazität zwischen den Elektroden des Quarzes und den Streukapazitäten aus dem Halterungssystem zusammensetzt. Der verlustbehaftete Serienresonanzkreis besteht aus einer dynamischen Induktivität L1, einer dynamischen Kapazität C1 und einem dynamischen Verlustwiderstand R1. Die dynamische Induktivität in dem Ersatzschaltbild entspricht der schwingenden Masse des Resonators und der Induktivität der Zuleitungen, die dynamische Kapazität entspricht der Elastizitätskonstanten des Quarzes und im dynamischen Verlustwiderstand sind die Verluste der inneren Reibung, die mechanischen Verluste im Halterungssystem und die akustischen Verluste in der Umgebung zusammengefasst. Für hohe Frequenzen muss das elektrische Ersatzschema noch durch einen Serienwiderstand für die ohmschen Verluste und eine Serieninduktivität für die elektrischen Anschlussleitungen erweitert werden.
- Erklärungen zum elektrischen Verhalten von Schwingquarzen
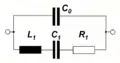Vereinfachte elektrische Ersatzschaltung eines Schwingquarzes
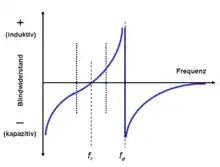Verlauf des Blindwiderstandes eines Schwingquarzes im Bereich der Resonanzfrequenz fr und der Antiresonanzfrequenz fa
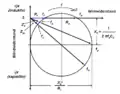Ortskurve des Blindwiderstandes eines Schwingquarzes
Mit einem Vektor-Netzwerkanalysator gemessene Daten eines 8-MHz-Schwingquarzes.
Gemessener Verlauf der Serienfrequenz (Marker 1), sowie durch C0 verursachte Parallelfrequenz (Marker 2) und Phasenwinkel eines Quarzes.
Ansicht der Nebenresonanzen eines Schwingquarzes.
In der Darstellung der Ortskurve des Scheinwiderstandes eines Schwingquarzes können weitere Begriffe, die mit den Eigenschaften des Schwingquarzes zusammenhängen, anschaulich erklärt werden:
Die Resonanzfrequenz fr tritt auf, wenn der Blindwiderstand X des Resonators gleich Null wird. Dazu gehört dann der Resonanzwiderstand Rr. Am hochohmigen Schnittpunkt des Ortskreises mit der reellen Achse befindet sich die Antiresonanzfrequenz fa mit dem zugehörigen Widerstand Ra. Die Verlängerung des Vektors der Serienresonanzfrequenz fs führt zur Parallelresonanz fp, dem Punkt, an dem der Quotient des Quadrats des Blindwiderstands der Parallelkapazität bei Serienresonanz X0 und des Verlustwiderstandes R1 (X02/R1) am größten ist. Die Frequenz, bei der die Impedanz des Quarzes den minimalen Wert erreicht, ist die Minimalimpedanzfrequenz fm. Die Stelle auf dem Ortskreis, an dem die Impedanz ihren Maximalwert erreicht, ist die Maximalimpedanzfrequenz fn.
Die Ersatzschaltung des Schwingquarzes hat also zwei Resonanzfrequenzen, bei denen der Scheinwiderstand reell ist, der Phasenwinkel also Null beträgt: die Resonanzfrequenz fr und die höhere Antiresonanzfrequenz fa. Zahlenmäßig entspricht die Resonanzfrequenz fr in etwa der Serienresonanzfrequenz fs, also der Resonanzfrequenz, die sich aus der Serienschaltung der dynamischen Bauelemente des Kristalls ergibt. Die Antiresonanzfrequenz fa wird dagegen oft mit der Parallelresonanzfrequenz fp verwechselt. Der Wert der Serienresonanzfrequenz fs ist unter Vernachlässigung des Verlustwiderstandes
Da die Ersatzschaltung des Schwingquarzes auch noch die parallel geschaltete statische Kapazität C0 enthält, kann die Resonanz, unter Einbeziehung dieser Kapazität, auch als Parallelresonanzfrequenz fp definiert werden:
Das Verhältnis der Parallelkapazität C0 zur dynamischen Kapazität C1 wird r genannt:
Der Abstand zwischen Serien- und Parallelresonanzfrequenz ist:
Oder vereinfacht für große Werte (r > 25):
Gütefaktor und Bandbreite
Der Gütefaktor Q eines Schwingquarzes, auch Schwingungsgüte genannt, kann, unter Vernachlässigung der statischen Kapazität C0, aus den Werten der dynamischen Kapazität C1, der dynamischen Induktivität L1 und dem dynamischen Verlustwiderstand R1 aus dem Ersatzschaltbild nach folgenden Formeln berechnet werden.
Gegenüber üblichen LC-Resonanzkreisen sind bei Schwingquarzen die Werte der dynamischen Induktivität L1 verhältnismäßig hoch, die der dynamischen Kapazität C1 äußerst niedrig, und die Werte der dynamischen Verlustwiderstände R1 bewegen sich im Bereich recht niedriger zweistelliger Ohm-Werte. Beispielsweise liegen die Werte bei einem handelsüblichen Schwingquarz mit 10 MHz bei L1 = 25 mH, C1 = 0,01 pF und R1 = 65 Ω. Aus diesen Werten errechnet sich der für Schwingquarze übliche, im Vergleich zu LC-Kreisen recht hohe Gütefaktor von 25.000.
Die Bandbreite B einer Resonanzschaltung wird durch die Beziehung
ausgedrückt. Bei dem obigen 10-MHz-Schwingquarz mit dem Gütefaktor 25.000 liegt somit die Bandbreite im Bereich von 400 Hz.
Anwendungen
Schwingquarze finden hauptsächlich Anwendung in der Elektrotechnik und Nachrichtentechnik und können über einen weiten Frequenzbereich hergestellt werden. Sie finden sich z. B. in praktisch allen Sendeanlagen, seltener in Empfängern, in Quarzuhren, als Taktgeber in Computern und Mikrocontrollern sowie in Frequenzzählern und digitalen Signalgeneratoren. Ebenso eignen sich Quarze zur Realisierung von Filtern.
Selbst als Konsumartikel haben Schwingquarze relative Fehlergrenzen in der Größenordnung 0,001 %. Derartig kleine Fehlergrenzen sind sonst in der Messtechnik nur mit extremem Aufwand oder gar nicht erreichbar.
- Bemerkung:
- 0,001 % = 10 ppm = 1 zu 100.000 ≈ 1 Sekunde pro Tag ≈ 30 Sekunden pro Monat
- Für Uhren stellt dies die übliche untere Grenze dar. Justierte Uhren weisen geringere Fehlergrenzen von unter 3 Sekunden pro Monat auf.
Mit entsprechend geschnittenen Quarzen sind durch den Temperaturgang der Resonanzfrequenz sehr genaue Temperatursensoren herstellbar.
In Beschichtungsanlagen dienen frei aufgehängte Schwingquarze der Messung der erreichten Schichtdicke, indem die Änderung ihrer Resonanzfrequenz verfolgt wird, die durch die Massenzunahme infolge der auf dem Quarz entstehenden Schicht entsteht.
Wenngleich sich Quarze durch die mechanische Bearbeitung für beliebige Resonanzfrequenzen innerhalb eines zulässigen Intervalls herstellen lassen, haben sich handelsüblich einige wesentliche Frequenzen ergeben. Auszugsweise sind dies:
| Frequenz in MHz | Primäre Anwendung |
|---|---|
| 0,032768 | Uhrenquarz in Echtzeituhren und elektromechanischen Quarzuhren in Form einer Stimmgabel; erlaubt eine Division durch 215, um einen Sekundenimpuls zu erhalten. |
| 1,8432 | Takt für UARTs; erlaubt ganzzahlige Divisionen zu üblichen Bitraten wie 9600 bps. |
| 3,579545 | Frequenz des Farbträgers in der US-Farbfernsehnorm NTSC. Aufgrund der weiten Verbreitung findet diese Frequenz auch bei dem Mehrfrequenzwahlverfahren im Telefoniebereich Anwendung. |
| 3,686400 | Takt für Mikrocontroller und UART; erlaubt ganzzahlige Divisionen zu üblichen Bitraten wie 9600 bps. |
| 4,43361875 | Frequenz des Farbträgers in der Farbfernsehnorm PAL. |
| 10,245 | Verwendet in älteren, analogen UKW-Radios, um die Zwischenfrequenz von 10,7 MHz auf 455 kHz zu mischen. |
| 11,0592 | Takt für Mikrocontroller und UART; erlaubt ganzzahlige Divisionen zu üblichen Bitraten wie 9600. |
| 11,2896 | Digitale Audiosysteme wie die Compact Disc (CD), welche mit einer Abtastrate von 44,1 kHz arbeiten. |
| 12,0000 | Verwendet bei USB-Geräten. |
| 12,288 | Digitale Audiosysteme wie Digital Audio Tape und Soundkarten, welche mit einer Abtastrate von 48 kHz arbeiten. |
| 25,000 | Anwendung bei Fast Ethernet und dem Media Independent Interface (MII). |
| 27,000 | Haupttakt bei digitalen Videogeräten wie DVD-Spielern. |
| 33,33 | Üblicher externer Takt für Hauptprozessoren vor der PLL |
- Grundwellenquarz: Aufdruck in kHz[30]
- Oberwellenquarz: Aufdruck in MHz
Normung
Die Normung von Schwingquarzen umfasst den gesamten Umfang der hierzu auftretenden Fragestellungen, angefangen vom synthetischen Quarzkristall über die Begriffe und die Anwendungen von Schwingquarzen bis hin zu den Messbedingungen zur Messung der elektrischen Parameter.
Die Definitionen und den Leitfaden zur Anwendung von synthetischen Quarzkristallen wird spezifiziert in der
- DIN EN 60758, Synthetischer Quarzkristall – Festlegungen und Leitfaden für die Anwendung
Die Grundbegriffe und die Definitionen für die Prüfungen der elektrischen Parameter der Schwingquarze sind festgelegt in der Fachgrundspezifikation sowie in den zugehörenden Rahmenspezifikationen:
- DIN EN 60122-1, Teil 1: Fachgrundspezifikation für Schwingquarze mit bewerteter Qualität
- DIN IEC 60122-2, Teil 2: Leitfaden zur Anwendung von Schwingquarzen zur Frequenzstabilisierung und -Selektion
- DIN IEC 60122-2-1, Teil 2: Leitfaden zur Anwendung von Schwingquarzen zur Frequenzstabilisierung und -Selektion zur Taktversorgung von Mikroprozessoren;
- DIN EN 60122-3, Teil 3: Norm-Gehäusemaße und Anschlussdrähte
Die Bedingungen für die Messvorschriften der elektrischen Parameter der Schwingquarze sind in den folgenden Normen festgelegt:
- DIN EN 60444-1, Messung der Resonanzfrequenz und des Resonanzwiderstandes von Schwingquarzen nach dem Null-Phasenverfahren in einem π-Netzwerk
- DIN EN 60444-2, Messung der dynamischen Kapazität von Schwingquarzen nach dem Phasenoffsetverfahren
- DIN EN 60444-3, Messung der Zwei-Pol-Parameter von Schwingquarzen bis 200 MHz mit Kompensation der Parallelkapazität Co
- DIN EN 60444-4, Messung der Lastresonanzfrequenz fL des Lastresonanzwiderstandes RL und Berechnung anderer hergeleiteter Werte von Schwingquarzen bis 30 MHz
- DIN EN 60444-5, Meßverfahren zur Bestimmung der Ersatzschaltungsparameter von Schwingquarzen mit automatischer Netzwerkanalysatortechnik und Fehlerkorrektur
- DIN EN 60444-6, Messung der Belastungsabhängigkeit (DLD)
- DIN EN 60444-7, Messung von Aktivitäts- und Frequenz-Dips von Schwingquarzen
- DIN EN 60444-8, Prüfaufbau für oberflächenmontierbare Schwingquarze
- DIN EN 60444-9, Messung der Nebenresonanzen von Schwingquarzen
Weitere Normen, die sich mit Bauelementen befassen, die direkt oder indirekt mit Schwingquarzen zusammen hängen, sind:
- DIN EN (IEC) 60679ff. Oszillatoren
- DIN EN (IEC) 60368ff. Quarzfilter
- DIN EN (IEC) 60862ff. & 61019ff. SAW-Filter & Resonatoren
- DIN EN (IEC) 61337ff. Dielektrische Resonatoren
Markt
Der Markt für Schwingquarze teilt sich auf in drei Bereiche. Einmal sind es die Schwingquarze als Einzelbauelemente, die von Anwendern separat in die entsprechenden Schaltungen eingebaut werden, zum anderen sind es die Quarzoszillatoren, die jeweils mit einem Quarzresonator, also einem Schwingquarz versehen sind. Die dritte Gruppe sind die sogenannten „Clock-Generatoren“, das sind die Stimmgabelquarze für Uhren. Es wird geschätzt, dass der weltweite Bedarf an Schwingquarzen im Jahre 2010 für jeden Bereich etwa den Wert von etwa 1,5 bis 1,8 Mrd. USD beträgt, so dass der Gesamtwert weltweit in etwa 4,5 bis 5,4 Mrd. USD beträgt.[31]
Literatur
- Bernd Neubig, Wolfgang Briese: Das große Quarzkochbuch. Franzis', Feldkirchen 1997, ISBN 3-7723-5853-5 (online).
Weblinks
Einzelnachweise
- Patent US2212845: Generating and transmitting electric currents. Angemeldet am 10. April 1918, veröffentlicht am 27. August 1940, Erfinder: Alexander M. Nicholson.
- A History of the Quartz Crystal Industry in the USA. Virgil E. Bottom, from the Proceedings of the 35th Annual Frequency Control Symposium 1981.
- Die erste Veröffentlichung über den praktischen Aufbau von Quarzoszillatoren erschien 1924 in: H. S. Shaw: Oscillating Crystals. In: QST Magazine Vol. XI, Nr. 7, 1924 (vgl. online). Siehe auch P. R. J. Brown: The influence of amateur radio on the development of the commercial market for quartz piezoelectric resonators in the United States. In: Proceedings of the 1996 IEEE International Frequency Control Symposium, 1996. 50th. IEEE, 1996, ISBN 0-7803-3309-8, doi:10.1109/FREQ.1996.559819.
- Warren A. Marrison: The Evolution of the Quartz Crystal Clock. In: The Bell System Technical Journal. Vol. XXVII, 1948, S. 510–588 (Reprint online (Memento des Originals vom 17. Juli 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.).
- Der Schwingquarz. Valvo-GmbH Hamburg, April 1964.
- Bernd Neubig, Wolfgang Briese: Das Grosse Quarzkochbuch. Franzis-Verlag, Feldkirchen 1997, ISBN 3-7723-5853-5. Kapitel 2 (PDF; 1,6 MB)
- QUARTZ CRYSTAL, THE TIMING MATERIAL, Fortiming Corporation
- Bernd Neubig: Moderne Technologien bei Schwingquarzen und Quarzoszillatoren.
- W. Briese: Eigenschaften von Schwingquarzen
- AT cut, Archivierte Kopie (Memento des Originals vom 6. November 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Darstellung von Quarzschnitten Archivierte Kopie (Memento des Originals vom 4. Dezember 2010 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Crystals and oscillators, Jerry A. Lichter (PDF)
- Crystal Technology, 4timing.com
- Crystal and frequency control glossary, Icmfg.com. Archivierte Kopie (Memento des Originals vom 6. November 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Paul W. Kruse, David Dale Skatrud: Uncooled infrared imaging arrays and systems. Academic Press, 1997, ISBN 0-12-752155-0, S. 273 (eingeschränkte Vorschau in der Google-Buchsuche).
- Crystals and oscillators, Jerry A. Lichter (PDF)
- Patent US4985687: Low power temperature-controlled frequency-stabilized oscillator.
- Patent US4499395: Cut angles for quartz crystal resonators.
- Jerry A. Lichter: Crystals and oscillators (PDF; 176 kB).
- Patent US4419600: Stress-compensated quartz resonators.
- Patent US5686779: High sensitivity temperature sensor and sensor array.
- Y Cut Crystal (Memento des Originals vom 30. Juli 2012 im Webarchiv archive.today) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.. Engineersedge.com (25. August 2009).
- UFFC|History (Memento des Originals vom 12. Mai 2009 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.. Ieee-uffc.org (23. März 1959).
- Glossary of terms used in the quartz oscillator-plate industry (PDF; 521 kB)
- All about Quartz Devices Archivierte Kopie (Memento des Originals vom 31. Mai 2010 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Martin Wucherer, Achim Krumrein: Quarze & Quarzoszillatoren. (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 2 MB)
- Quartz Crystal Basics: From Raw Materials to Oscillators, Ken Hennessy, NDK America, Inc; publiziert in High Frequency Electronics Heft Dezember 2007 Vol. 6 Nr. 12 (PDF)
- Wintron plant tour.
- Frequency Electronics, Inc., Tutorial, Precision Frequency Generation (PDF)
- Frank Sichla – HF-Technik mit dem NE/SA612 – beam-Verlag ISBN 978-3-88976-054-8
- Karin Zühlke: Unser Ziel ist es, den Quarz obsolet werden zu lassen. (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. In: Markt & Technik. Nr. 27, 2. Juli 2010. (Interview mit Markus Lutz von SiTime)
