Bravais-Gitter
Die Bravais-Gitter sind eine Einteilung der möglichen Gittersysteme (Translationsgruppen) in der Kristallographie:
mit ganzen Zahlen und linear unabhängigen Vektoren (im Fall von drei Dimensionen), die das Gitter aufspannen (primitive Vektoren). Bravais-Gitter sind Teil der Klassifikation der Raumgruppen (und die mathematische Ableitung der Klassifikation der Bravais-Gitter findet sich in der zugehörigen Literatur).[1] Die Bravais-Gitter sind also eine Klassifikation der möglichen Translationsgruppen regelmäßiger Punktgitter.[2]
In drei Dimensionen gibt es vierzehn Bravais-Gitter.[3]
Bei der Darstellung der Bravais-Gitter geht man traditionell von den Punktgruppen und deren Einteilung in sieben Kristallsysteme (bzw. 32 Kristallklassen, Typen von Punktgruppen) aus. Aus der Basiszelle des Kristallsystems entstehen die Bravais-Gitter durch Translation und sie werden durch Addition weiterer Gitterpunkte zur Basiszelle konstruiert. Hierbei ist die Basiszelle der Symmetriegruppe des Kristallsystems angepasst (vergleiche die Diskussion bei Elementarzelle und die Darstellung weiter unten). Für die Bravais-Gitter müssen im Allgemeinen noch weitere Gitterpunkte hinzugefügt werden (die als Ausgangspunkt gewählte Basiszelle entspricht nicht der primitiven Elementarzelle des Gitters). Das kann auf sechs mögliche Arten geschehen: flächenzentriert – in jeweils gegenüberliegende Seiten (A, B, C) oder in jeder Fläche (F) – raumzentriert (I) und primitiv (P, das heißt keine Addition von zusätzlichen Gitterpunkten).[4]
Während die Punktgruppen-Symmetrien in der äußeren Kristallform sichtbar sind und aus den Symmetrieelementen Drehung, Spiegelung, Inversion und Drehinversion bestehen, kommen bei der Klassifizierung in den Bravais-Gittern die Translationen hinzu, die im Kristallgitter von mikroskopischer Größenordnung (Ångström) sind und nicht in der äußeren Kristallform sichtbar.
Dabei werden alle Gitterpunkte als gleichwertig betrachtet. Bei der Beschreibung der Kristallstruktur kommt im Allgemeinen zum mathematischen Gitter (definiert über die möglichen Translationen) noch die Beschreibung der Basis hinzu, die auch aus mehreren Atomen bestehen kann (Kristallstruktur ist gleich Gitter plus Basis).
Auguste Bravais klassifizierte um 1849[5] die verschiedenen möglichen Translationsgitter, indem er gleiche parallelepipede Zellen in alle Richtungen aneinander legte. Die Ecken der Zellen ergeben dann ein dreidimensionales Punktgitter, die im realen Kristall die Schwerpunkte der Kristallbausteine (z. B. Atome oder Moleküle) darstellen.
Im Allgemeinen ist das erzeugende Parallelepiped ein schiefes Prisma, bei dem sich alle drei Seitenlängen und Winkel voneinander unterscheiden. In diesem Fall handelt es sich um ein triklines Kristallsystem. Genügen die Seitenlängen und/oder Winkel weiteren Bedingungen, so können sich höhere Symmetrien ergeben. Das kubische Kristallsystem verlangt beispielsweise rechte Winkel und gleich lange Zellkanten. Bravais fiel auf, dass es Gittertypen gibt, die eine Besonderheit aufweisen: Ihre Symmetrie ist höher als an der kleinsten möglichen Zelle ohne weiteres erkennbar wäre. Beim Halit ist es möglich, die halbe Flächendiagonale eines Würfels als Translation zu wählen. Das entstehende Gitter hat jedoch ein Rhomboeder mit dem Winkel von 70° 31' 44" als kleinstes Parallelepiped. Aus Symmetriegründen ist es viel zweckmäßiger, aus dem Gitter einen Würfel als sogenannte Elementarzelle herauszugreifen. Diese kubische Elementarzelle ist größer als der Rhomboeder und enthält in der Mitte jeder Fläche einen weiteren Gitterpunkt. Dieses Gitter wird kubisch flächenzentriert genannt.
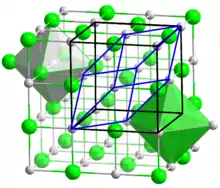
Verwendung
Der eigentlich rein mathematische Begriff des Bravais-Gitters findet oft Verwendung in den Naturwissenschaften, wie etwa der Kristallographie, Mineralogie, Materialwissenschaft, Festkörperchemie oder der Festkörperphysik, da sich so die Anordnung der Atome innerhalb eines Kristalls systematisch beschreiben lässt. Hierbei ist jedoch nicht notwendigerweise jeder Gitterpunkt durch ein Atom repräsentiert: Das Bravais-Gitter liefert ausschließlich das mathematische Gerüst, das in einer Kristallstruktur durch Atome (die Basis) aufgefüllt wird. Die Kristallstruktur besteht somit aus dem Gitter und der Basis, welche sich an jedem Gitterpunkt wiederholt, und wird in der Kristallographie als fundamentales Prinzip verstanden. So ergibt sich z. B. die NaCl-Struktur aus einem kubisch-flächenzentrierten Gitter und einer zweiatomigen Basis je eines Na-Kations und Cl-Anions.
Eine besondere Bedeutung hat es bei der Strukturaufklärung von Kristallen (insbesondere Röntgenkristallographie). Anhand der Metrik der Reflexe im reziproken Raum und deren systematischer integraler Auslöschung kann das Bravais-Gitter des Kristalls bestimmt werden.
Klassifikation
Die Bravais-Gitter werden anhand ihrer Punktgruppe den sieben Kristallsystemen zugeordnet. Entspricht die Basiszelle des Bravais-Gitters einer primitiven Elementarzelle des Kristallgitters – sie hat dann das kleinstmögliche Volumen (die Zelle enthält einen Punkt) – spricht man von einem primitiven Gitter.
Die weitere Differenzierung der sieben Kristallsysteme zu den 14 Bravais-Gittern erfolgt durch Anordnung weiterer Gitterpunkte, entweder in der Raummitte (raumzentriert oder innenzentriert), auf den Mittelpunkten aller Begrenzungsflächen (flächenzentriert) oder auf den Mittelpunkten der zwei Basisflächen (basiszentriert) der Elementarzelle.
Im Folgenden sind die Bravais-Gitter nach den Kristallsystemen, mit abnehmender Symmetrie, geordnet.
Kubisches Kristallsystem
- höchste Symmetrie
- drei gleich lange Achsen im 90°-Winkel
kubisch -primitiv -raumzentriert -flächenzentriert 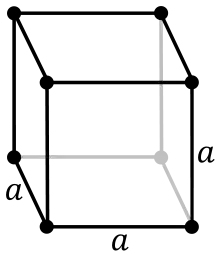
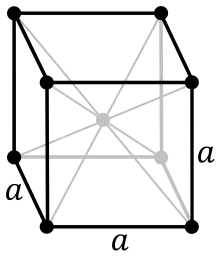

(sc: simple cubic) (bcc: body centered cubic) (fcc: face centered cubic)
Tetragonales Kristallsystem
- zwei gleich lange Achsen, drei 90°-Winkel
tetragonal -primitiv -raumzentriert 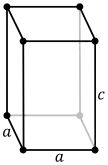
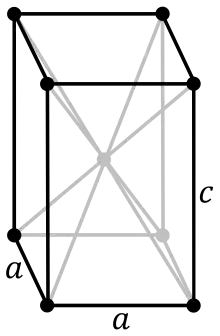
Orthorhombisches Kristallsystem
- auch Rhombisches Kristallsystem
- drei 90°-Winkel, keine gleich langen Achsen
orthorhombisch -primitiv -basiszentriert -raumzentriert -flächenzentriert 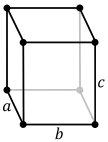



Hexagonales Kristallsystem
- zwei gleich lange Achsen in einer Ebene im 120°-Winkel, die dritte Achse senkrecht dazu
hexagonal-primitiv 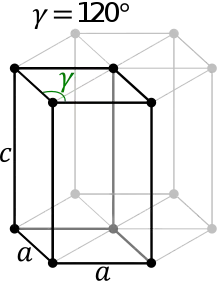
Trigonales Kristallsystem
- Trigonale Kristallstrukturen können ebenfalls im hexagonalen Gitter beschrieben werden:
- hexagonale Aufstellung: a = b ≠ c , α = β = 90° , γ = 120° (siehe Abbildung oben)
- Als Spezialfall kann eine rhomboedrische Zentrierung auftreten:
- drei gleich lange Achsen, drei gleiche Winkel ungleich 90° (siehe Abbildung unten)
- nicht mit dem orthorhombischen Kristallsystem zu verwechseln
rhomboedrisch 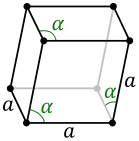
Monoklines Kristallsystem
- zwei 90°-Winkel, keine gleich langen Achsen
monoklin -primitiv -basiszentriert 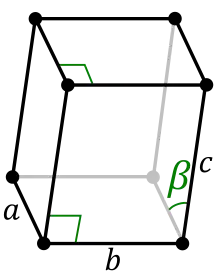
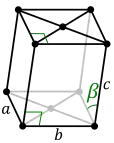
Triklines Kristallsystem
- geringste Symmetrie aller Gitter
- keine gleichen Winkel, keine gleich langen Achsen
triklin 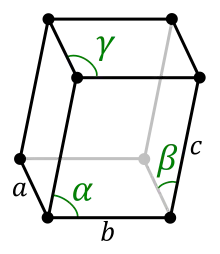
Hermann-Mauguin-Symbolik
In der Hermann-Mauguin-Symbolik (siehe auch Punktlage):
- Triklin, P1
- Monoklin: primitiv P2/m, basis-flächenzentriert C2/m
- Orthorhombisch: primitiv Pmmm, innenzentriert Immm, basisflächenzentriert Cmmm, flächenzentriert Fmmm
- Hexagonal: P6/mmm
- Rhomboedrisch: R3m
- Tetragonal: primitiv P4/mmm, innenzentriert I4/mmm
- Kubisch: primitiv Pm3m, innenzentriert Im3m, flächenzentriert Fm3m
Bravais-Gitter in nicht-dreidimensionalen Räumen
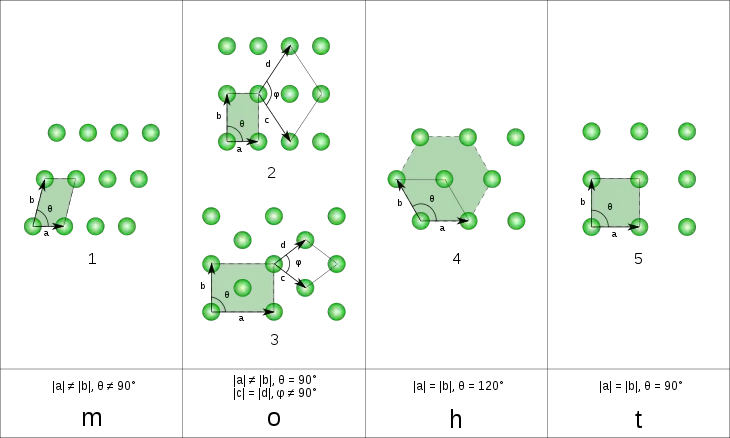
Im Zweidimensionalen gibt es fünf Bravais-Gitter, davon vier primitive:[6] das schiefwinklige Gitter sowie vier spezielle Typen: das quadratische, das rechteckige, das hexagonale sowie das zentriert-rechteckige Gitter, welches als einziges nicht primitiv ist. Die Oberfläche aller dreidimensionalen Gittertypen besteht aus diesen zweidimensionalen Gittertypen. Sie haben daher in der Oberflächenphysik sowie der Nanotechnologie eine große Bedeutung.
 Die fünf zweidimensionalen Bravais-Gitter:
Die fünf zweidimensionalen Bravais-Gitter:
1: schiefwinklig, 2: rechtwinklig, 3: zentriert-rechteckig, 4: hexagonal, 5: quadratisch.
Die Einheitszellen sind grün hinterlegt, während die reduzierten Zellen durch die Basisvektoren aufgespannt werden und mit durchgezogener Linie dargestellt sind.
Im Vierdimensionalen gibt es 64 Bravais-Gitter (10 davon zerfallen in enantiomorphe Paare, zählt man dies nicht mit, sind es 54).[7]
Siehe auch
Weblinks
Einzelnachweise
- z. B. Johann Jakob Burckhardt Die Bewegungsgruppen der Kristallographie, 2. Auflage, Birkhäuser, 1966.
- Okrusch, Matthes Mineralogie, Springer Verlag 2005, S. 9f.
- Helmut G. F. Winkler (1950): Hundert Jahre Bravais Gitter. In: Die Naturwissenschaften, Band 37, Nummer 17, Seiten 385–390 doi:10.1007/BF00738360.
- Sanat Chatterjee Crystallography and the World of Symmetry, Springer Verlag 2008, S. 28f (Abschnitt Bravais-Gitter).
- Bravais: Abhandlung über die Systeme von regelmäßig auf einer Ebene oder im Raum vertheilten Punkten, Leipzig 1897, französisches Original J. Ecole Polytechnique, Band 19, 1850, S. 1–128.
- Martin Henzler, Wolfgang Göpel: Oberflächenphysik des Festkörpers. Teubner, Stuttgart 1994, ISBN 3-519-13047-5.
- Harold Brown, J. Neubüser, H. Wondratschek, R. Bülow, Hans Zassenhaus Crystallographic groups of four dimensional space, Wiley 1978.