Spiegelung (Geometrie)

Spiegelungen sind in der Geometrie bestimmte Kongruenzabbildungen der Zeichenebene oder des (euklidischen) Raumes. Eine Gleitspiegelung ist die Kombination aus einer Spiegelung und einer Translation. Daneben gibt es Schrägspiegelungen, die keine Kongruenzabbildungen sind.

Punktspiegelung

Halbieren der Verbindungsstrecke; Halbdrehung

Es handelt sich um eine Abbildung, die durch einen Punkt Z (Spiegelpunkt, Zentrum) gegeben ist. Die Spiegelung am Punkt Z ordnet jedem Punkt P der Zeichenebene oder des Raumes einen Bildpunkt P' zu, der dadurch bestimmt ist, dass die Verbindungsstrecke [PP'] vom Punkt Z halbiert wird.

Eine Punktspiegelung am Koordinatenursprung wird als Raumspiegelung oder Inversion bezeichnet; man beachte, dass die Bezeichnung Inversion jedoch häufig auch für eine Spiegelung an einem Kreis benutzt wird.

Eine Punktspiegelung hat genau einen Fixpunkt (das heißt einen Punkt, den die Abbildung unverändert lässt), nämlich das Zentrum Z. Fixgeraden (also die Geraden, die die Abbildung in sich selbst überführt) sind genau die Geraden durch Z. Eine beliebige Gerade g wird auf eine zu g parallele Gerade (Bildgerade) g′ abgebildet.

In der Ebene ist die Punktspiegelung am Zentrum Z gleichbedeutend mit einer Drehung um 180° um das Drehzentrum Z.

Punktspiegelungen sind geraden-, längen- und winkeltreu, also Kongruenzabbildungen.

Jede ebene Punktspiegelung lässt sich ersetzen durch zwei hintereinander ausgeführte Achsenspiegelungen, wobei die Achsen dieser Spiegelungen durch das Zentrum Z gehen und zueinander senkrecht sind. Die Reihenfolge dieser Spiegelungen ist daher beliebig.

Jede räumliche Punktspiegelung lässt sich ersetzen durch drei hintereinander ausgeführte Ebenenspiegelungen, wobei die drei Spiegelebenen durch das Zentrum Z gehen und zueinander senkrecht sind. Die Reihenfolge dieser Spiegelungen ist daher beliebig.

In der Kristallographie wird eine Punktspiegelung Inversion bzw. der Punkt Inversionszentrum und die Achsen auch Drehinversionachsen genannt und mit dem Hermann-Mauguin-Symbol 1 gekennzeichnet.[1]

Synthetische Geometrie

In der synthetischen Geometrie kann eine Punktspiegelung in jeder affinen Translationsebene, die dem (affinen) Fano-Axiom genügt, definiert werden. Dazu wird das Zentrum der Punktspiegelung $O$ als Ursprung fest gewählt und jedem Punkt $P$ der Ebene umkehrbar eindeutig die Translation ${\overrightarrow {OP}}$ als Orts"vektor" zugeordnet. Die Punktspiegelung wird durch ${\overrightarrow {OP}}\mapsto {\overrightarrow {PO}}$ definiert und es gilt:

Zu jedem Punkt $O$ existiert genau eine Punktspiegelung an diesem Punkt,
jede Punktspiegelung ist eine teilverhältnistreue Kollineation, also eine Affinität,
jede Punktspiegelung ist involutorisch,
die Punktspiegelung an $O$ ist durch den spurtreuen Endomorphismus −1 der Translationsgruppe induziert und demnach eine zentrische Streckung (→ siehe Dilatation) mit dem Streckungsfaktor −1,
in einer präeuklidischen Ebene zählen die Punktspiegelungen zu den Kongruenzabbildungen.

→ Siehe zu den verwendeten verallgemeinerten Begriffen den Artikel „Affine Translationsebene“, für eine Definition von Punktspiegelungen in beliebigen affinen Ebenen, die die hier gegebene Definition verallgemeinert, den Artikel „Fano-Axiom“.

Achsenspiegelung

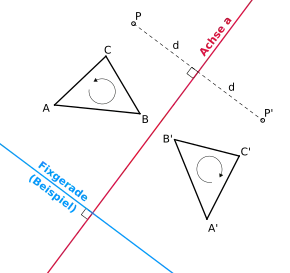
Rechtwinkliges Halbieren, Änderung des Umlaufsinns, Fixgeraden (rot und blau)

Eine Achsenspiegelung (auch Geradenspiegelung) ist durch eine Gerade a (Spiegelachse oder kurz Achse) gegeben. Sie ordnet jedem Punkt P einen Bildpunkt P′ zu, der dadurch bestimmt ist, dass die Verbindungsstrecke [PP′] von der Achse a rechtwinklig halbiert wird.

Die Fixpunkte einer Achsenspiegelung sind genau die Punkte von a. Man spricht daher auch von der Fixpunktgeraden a. Die Fixgeraden der Achsenspiegelung sind genau die Achse a selbst sowie alle Lotgeraden zur Achse. Im räumlichen Fall gibt es auch Fixebenen, nämlich die zur Achse a orthogonalen Ebenen.

Auch die Achsenspiegelung ist eine Kongruenzabbildung.

Wenn zwei kongruente Objekte in der Ebene vorliegen, können diese in jedem Fall durch Komposition (Verkettung, Hintereinanderausführung) von höchstens drei Achsenspiegelungen ineinander übergeführt werden. Die Achsenspiegelung kann deshalb als ein Grundbegriff der metrischen Geometrie der Ebene verwendet werden.

In der Ebene ist zu beachten, dass durch eine Achsenspiegelung die Orientierung (der Umlaufsinn) eines Dreiecks geändert wird. Sie ist hier also keine eigentliche Bewegung, das heißt, sie kann nicht durch eine physikalische Bewegung verwirklicht werden, ohne dass das Objekt die Ebene verlässt.

Im dreidimensionalen Raum entspricht die Achsenspiegelung einer Drehung um 180° um die Spiegelachse. Ein Objekt, das zusammen mit der Spiegelachse in einer Ebene liegt, wird dabei in die gleiche Ebene „umgeklappt“; dies ist die Bewegung, die bei der Beschränkung auf eine Ebene nicht möglich war.

Synthetische Geometrie

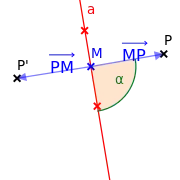
Zur Definition einer senkrechten Achsenspiegelung in einer präeuklidischen Ebene.

In der synthetischen Geometrie definiert man etwas allgemeiner eine (senkrechte) Achsenspiegelung für allgemeinere affine Ebenen, die präeuklidischen Ebenen. Hier versteht man unter der Spiegelung $\sigma _{a}$ an der Geraden $a$ (der Achse) diejenige Abbildung der Ebene auf sich, die jedem Punkt $P$ denjenigen Punkt $\sigma _{a}(P)$ zuordnet, der auf der Lotgeraden zu $a$ durch $P$ liegt, und dadurch bestimmt ist, dass der Schnittpunkt dieser Lotgeraden mit $a$ der Mittelpunkt von $(P,\sigma _{a}(P))$ ist. Vergleiche dazu die Abbildung rechts: Der Winkel $\alpha$ ist ein Rechter, die gekennzeichneten Vektoren ${\overrightarrow {MP}}$ und ${\overrightarrow {PM}}={\overrightarrow {MP'}}$ sind zueinander invers, das heißt, $M$ ist der Mittelpunkt der Strecke $PP'$ . Dadurch ist das Bild $P'=\sigma _{a}(P)$ von $P$ unter der Achsenspiegelung an $a$ eindeutig definiert.

Für diese senkrechten Achsenspiegelungen gilt:

Zu jeder Geraden $a$ gibt es genau eine Achsenspiegelung $\sigma _{a}$ ,
jede Achsenspiegelung ist eine teilverhältnistreue Kollineation, also eine Affinität,
Fixpunkte der Achsenspiegelung sind genau die Punkte ihrer Achse,
die Fixgeraden einer Achsenspiegelung sind genau die Spiegelachse und alle zu ihr senkrechten Geraden.

Ebenenspiegelung

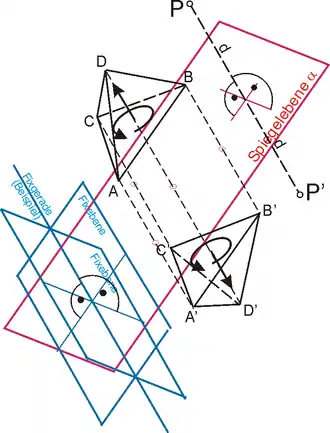
Rechtwinkliges Halbieren, Änderung der Simplexorientierung, Fixelemente (rot und blau)

Diese weitere Art der Spiegelung kommt nur in der Raumgeometrie vor. Sie ist gegeben durch eine Ebene α, die Spiegelebene. Der Bildpunkt von P ist dadurch bestimmt, dass die Verbindungsstrecke zwischen ihm und seinem Bildpunkt P′ von der Spiegelebene rechtwinklig halbiert wird.

Fixpunkte sind genau die Punkte der Spiegelebene. Fixgeraden sind die Geraden der Spiegelebene sowie die Geraden, die zu dieser orthogonal verlaufen. Fixebenen sind die Spiegelebene und die zu ihr orthogonalen Ebenen.

Die Ebenenspiegelung verändert die Orientierung eines Simplex′. Auch sie ist also keine „eigentliche“ Bewegung: Ein Tetraeder lässt sich nicht physisch in sein Spiegelbild überführen.

In der Kristallographie wird die Spiegelung mit dem Hermann-Mauguin-Symbol m bezeichnet.

Spiegelungen in Räumen beliebiger Dimension

In einem n-dimensionalen euklidischen Raum gibt es n Arten von Spiegelungen, nämlich Spiegelungen an 0, 1,… (n-1)-dimensionalen Teilräumen (Spiegelelementen).

Fixpunkte sind stets die Punkte des Spiegelelements. Höherdimensionale Fixelemente sind dessen Teilräume sowie die Teilräume, die zu diesem orthogonal sind.

Die Spiegelung an einem (n-1)-dimensionalen Teilraum lässt sich jeweils nicht als „eigentliche Bewegung“ im n-dimensionalen Raum verstehen. Bei Einbettung in einen (n+1)-dimensionalen Raum wird sie gleichbedeutend mit einer involutorischen Drehung um das Spiegelelement.

Hieraus ergibt sich unter anderem, dass im eindimensionalen Fall (also auf einer Geraden) die Punktspiegelung die einzig mögliche Spiegelung ist, und dass diese, da sie die Reihenfolge der Punkte umkehrt, ohne Verlassen der Geraden nicht als Bewegung verstanden werden kann.

Siehe auch

Spiegelungsmatrix (Lineare Algebra)
Spiegelung (Darstellende Geometrie)

Literatur

H. Schupp: Elementargeometrie. UTB Schöningh, 1977, ISBN 3-506-99189-2
Friedrich Bachmann: Aufbau der Geometrie aus dem Spiegelungsbegriff. 2. Auflage, Berlin; Göttingen; Heidelberg 1973
Zusammenfassung: Zur Begründung der Geometrie aus dem Spiegelungsbegriff. In: Mathematische Annalen, Band 123, 1951, S. 341 ff.
Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.

Weblinks

Commons: Reflection (geometry) – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Spiegelung. In: MathWorld (englisch).

Einzelnachweise

W. Borchardt-Ott: Kristallographie: Eine Einführung für Naturwissenschaftler. Springer-Verlag, 2013, ISBN 978-3-662-08227-0, S. 39 (books.google.de).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] W. Borchardt-Ott: Kristallographie: Eine Einführung für Naturwissenschaftler. Springer-Verlag, 2013, ISBN 978-3-662-08227-0, S. 39 (books.google.de).