Versetzung (Materialwissenschaft)

Die Versetzung ist eine Störung der Periodizität eines Kristallgitters, die sich längs einer Linie im Kristall fortsetzt. Sie kann beispielsweise entstehen

beim Kristallwachstum (z. B. aus der Schmelze oder in Gasphasenabscheidung),
im bestehenden Kristall infolge von Eigenspannungen
oder bei der plastischen Verformung. Plastische Verformung von Kristallen erfolgt unter Erzeugung und Bewegung von Versetzungen (Bild 1) oder durch Zwillingsbildung.

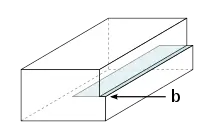
Bild 1. Gleitstufe und betätigte Gleitebene, deren Rand die Lage der erzeugten Versetzung markiert. Der Burgersvektor b ist dem Gleitvektor g gleich

Bild 2. Spannungsfelder einer Stufenversetzung in einem Kristall mit kubisch-primitivem (kp) Gitter
(Blick entlang der Versetzungslinie)

Die Versetzung kann nicht im Inneren eines Kristalls enden. Man unterscheidet traditionell zwei idealisierte Modelle von Versetzungen: die Stufenversetzung und die Schraubenversetzung. Ein wichtiges Merkmal zur Charakterisierung einer Versetzung ist der Burgersvektor.[1]

Idealisierte Grundmodelle

Es gibt zwei Grundmodelle von Versetzungen, die es erlauben, aus der Verzerrung des Kristallgitters die Versetzungsenergie theoretisch zu bestimmen. Die Idealisierung besteht vor allem in der Annahme, dass die Versetzungslinie gerade ist.

Stufenversetzung

Bild 3. Schema einer Stufenversetzung

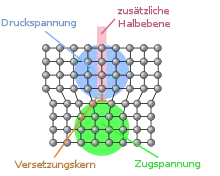
Burgersvektor und Versetzungslinie stehen senkrecht zueinander. Dies gilt allerdings nur für Kristallgitter, in denen infolge höherer Symmetrie rechte Winkel vorkommen, nicht im triklinen Kristallgitter. Eine Stufenversetzung kann man sich als eine zusätzliche Halbebene von Teilchen (Atome, Ionen) vorstellen, die in einem perfekten Kristall keine Fortsetzung besitzt. Die englische Bezeichnung der Stufenversetzung lautet edge dislocation. Die russische Bezeichnung ist краевая дислокация, deutsch: Randversetzung. Den Ort, wo diese Halbebene endet, nennt man Versetzungskern oder Versetzungslinie. Dort bewirkt die Versetzung die stärkste Verzerrung des Gitters, was ein Verzerrungsfeld um die Versetzungslinie herum ergibt (Bild 2).

Die Energie einer Stufenversetzung pro Längeneinheit $l$ beträgt

{\frac {E_{\text{Stufe}}}{l}}\approx {\tfrac {3}{4}}G\cdot b^{2}

mit G = Schubmodul.

Schraubenversetzung

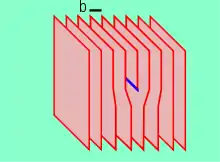
Bild 4. Schema einer Schraubenversetzung

Burgersvektor und Versetzungslinie liegen parallel. Eine Schraubenversetzung bewirkt einen schraubenförmigen Zusammenhang aller von ihr geschnittenen Gitterebenen.

Die Energie einer Schraubenversetzung pro Längeneinheit ist geringer als bei der Stufenversetzung:

{\frac {E_{\text{Schraube}}}{l}}\approx {\tfrac {1}{2}}G\cdot b^{2}

Der typische Versetzungsring weist daher mehr Bereiche mit Schrauben- als mit Stufencharakter auf und hat Ellipsenform.

Eigenschaften

Jede Versetzung hat zwei wichtige Parameter: die Versetzungslinie und den Burgersvektor.

Burgersvektor

Bild 5. Ermittlung des Burgersvektors

Der Burgersvektor ${\vec {b}}$ (benannt nach Johannes Martinus Burgers) beschreibt die Richtung, in der die Versetzungsbewegung unbedingt vorkommt. Sein Betrag entspricht der Entfernung zwischen zwei benachbarten Atomen in dieser Richtung. Seine Richtung wird von der Kristallstruktur des Materials diktiert.

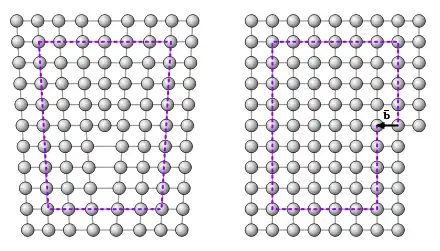
Der Burgersvektor lässt sich nach folgender Vorgehensweise (Bild 5) bilden:

Mit etwas Abstand zur Versetzung wird eine Verbindung zwischen den Atomen gezogen, sodass ein geschlossener Umlauf entsteht. Dies ist der Burgers-Umlauf, dargestellt durch die gestrichelte Linie im linken Bild.
Nun wird der Umlauf des linken Bildes 1:1 auf das rechte Bild eines ungestörten Kristalls übertragen.
An einer Stelle lässt sich der Umlauf nicht schließen.
Die zum Schließen des Umlaufs nötige Verbindung ist der Burgersvektor ${\vec {b}}$ .

Zu einem analogen Ergebnis führt es, wenn der geschlossene Umlauf im perfekten Gitter konstruiert wird und auf die Umgebung der Versetzungslinie übertragen wird. Der Burgersvektor mit der niedrigsten Energie (wächst mit dem Quadrat seines Betrages) liegt in dichtgepackten Ebenen:

In einem kubisch flächenzentrierten Gitter sind das die <110>-Richtungen in den {111}-Ebenen.
In einem kubisch raumzentrierten Gitter sind es die <111>-Richtungen in den {110}-Ebenen. Allerdings sind die {112}- und {123}-Ebenen nur geringfügig weniger dicht gepackt und können somit auch als Gleitebenen auftreten.

In den meisten metallischen Materialien ist die Länge oder der Betrag des Burgersvektors für eine Versetzung von der Größe eines interatomaren Abstandes. Der Betrag des Burgersvektors $\|\mathbf {b} \|\$ kann in krz und Kfz Gittern berechnet werden durch den Gitterparameter $a$ und den Komponenten des Burgersvektors $\langle hkl\rangle$ .

\|\mathbf {b} \|\ =(a/2){\sqrt {h^{2}+k^{2}+l^{2}}}

Die Energie eines Kristalls kann absinken, wenn sich die Versetzung in zwei Partialversetzungen mit jeweils nur halb so großem Burgersvektor aufspaltet. Im kfz-Gitter sind besonders die Shockley-Versetzungen interessant. Durch Kombination von zwei Shockley-Versetzungen kann dann wiederum eine sogenannte Lomer-Cotrell-Versetzung gebildet werden, die eine weitere Absenkung der Energie herbeiführt. Lomer-Cotrell-Versetzungen sind oftmals „sesshaft“, können sich also nicht weiter bewegen, da sie in einer anderen Ebene als die Ausgangsversetzung liegen.

Sichtbarmachung

Bild 6. TEM-Aufnahme von Versetzungen in Austenit.

Die Gitterverzerrungen um eine Versetzungslinie können mit einer Reihe von Methoden sichtbar gemacht werden. Diese eignen sich grundsätzlich auch zur Bestimmung der Versetzungsdichte ρ (siehe dort). Aus einem Diffraktogramm lassen sich durch die Halbwertsbreite der Reflexe Rückschlüsse über intrinsische Spannungen und damit die Versetzungsdichte schließen ohne diese sichtbar zu machen.

Ätzen
IR-Mikroskopie
Transmissionselektronenmikroskopie (TEM)
Feldionenmikroskopie (FIM)
Röntgentopographie

Des Weiteren ist es in jüngerer Zeit mittels hochauflösender Transmissionselektronenmikroskopie (HR-TEM) in Stahl (Bild 6) und einigen Halbleitern gelungen, Versetzungskerne in nahezu atomarer Auflösung sichtbar zu machen.

Versetzungsbewegung als Erklärung der Plastizität

Ehemals verwendetes Konzept der theoretischen Festigkeit

Bis in die 1930er Jahre war es eine große Herausforderung, die Plastizität und Festigkeit der Metalle auf mikroskopischer Ebene zu erklären. In einem „defektfreien“ Kristall wird die theoretische Festigkeit $\tau _{m}$ beschrieben durch den Ausdruck

\tau _{m}={\frac {G}{2\pi }}

$G$ = Schubmodul.

Diese Abschätzung resultiert aus Betrachtungen zum Verschiebewiderstand zweier übereinanderliegender Atomlagen. Die tatsächlich beobachteten Werte liegen jedoch für praktisch alle Metalle ein Vielfaches unter dieser Abschätzung. Bei kubisch-raumzentrierten Kristallgittern wird die theoretische Festigkeit um den Faktor 100 verfehlt, bei kubisch-flächenzentrierten und hexagonalen Gittern um den Faktor 1.000 bis 10.000.[1]

Entdeckung und Beschreibung von Versetzungen

1934 beschrieben Egon Orowan,[2] Michael Polanyi[3] und G. I. Taylor[4] unabhängig und etwa gleichzeitig, wie dieser Widerspruch durch das Versetzungskonzept aufgelöst werden kann. In den 1950er-Jahren wurde ihr Konzept unter Zuhilfenahme von neu entwickelten Elektronenmikroskopen, die Versetzungen sichtbar machen konnten, erstmal experimentell bestätigt.[1]

Bei der Ermittlung der theoretischen Festigkeit ging man davon aus, dass alle Atome einer Atomlage gleichzeitig den Verschiebewiderstand überwinden müssten.[1] Nach dem Versetzungskonzept ist das jedoch nicht der Fall: Unter der Wirkung einer im Vergleich zur theoretischen Festigkeit sehr kleinen Schubspannung können sich Versetzungen „bewegen“, d. h., die Atome der benachbarten Halbebene brechen ihre Bindungen kurzzeitig auf und binden sich an die der nächsten Halbebene an. Die Versetzungslinie „wandert“. Dies ist der elementare Mechanismus der plastischen Verformung. Er geschieht immer nur in solchen Gleitebenen, in denen auch der Burgersvektor liegt. Außer bei reinen Schraubenversetzungen, die auch quergleiten können, ist durch die Lage der Versetzung die Gleitebene bereits fest vorgegeben.

Versetzungswechselwirkungen

Gegensätzliche Versetzungen ziehen sich durch das von ihnen verzerrte Gitter an und annihilieren sich, wenn sie aufeinandertreffen. Versetzungen verschiedenen Typus oder Orientierung stören und behindern sich hingegen gegenseitig. Die reduzierte Mobilität resultiert in einer Ansammlung von Versetzungshaufen und zunehmender kaltverfestigung des Gefüges. An Korngrenzen stauen sich Versetzungen auf (Hall-Petch-Beziehung). Fremdatome wechselwirken auf mehrere Art mit Versetzungen und führen zu Mischkristallverfestigung. Je nach Art, Kohärenz und Größe von intermetallischen Phasen werden Versetzungsbewegungen an ihnen behindert (Ausscheidungshärtung und Dispersionshärtung).

Versetzungsmultiplikation

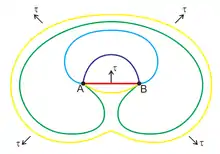
Bild 7. Frank-Read-Quelle zwischen zwei Hindernissen A und B

Die Bewegung einer Versetzungslinie kann durch die Wechselwirkung mit Leerstellen, anderen Versetzungen oder Ausscheidungen wie Carbiden gestört werden. Dies behindert den Gleitprozess. Laufen mehrere Versetzungen aufeinander auf, überlagern sich die Spannungsfelder und führen dazu, dass die Versetzung zwischen zwei Hindernissen ausbeult. Die nachfolgenden Versetzungen nehmen nun die Plätze der vorherigen Versetzungen ein. Es entsteht eine sogenannte Frank-Read-Quelle (Bild 7), die in realen Kristallen über einhundert neue Versetzungen aussenden kann.[1] Die Versetzungsmultiplikation führt zu Kaltverfestigung.

Die Kaltverfestigung ist irreversibel, solange die Temperatur unterhalb ca. 30 % der absoluten Schmelztemperatur T_m (in Kelvin) bleibt. Darüber kann es zur Ausheilung (Kristallerholung) der Versetzungen kommen durch Rekombination oder Anordnung der Versetzungen zueinander, wodurch die Festigkeit wieder deutlich sinkt und die Verformbarkeit steigt. Bei noch höheren Temperaturen werden die Versetzungen durch Gefügeneubildung beim Rekristallisationsglühen beseitigt.

Versetzungen in Halbleitern

In der Halbleiterindustrie werden möglichst versetzungsarme Einkristalle benötigt, da sonst die elektronischen Eigenschaften der Kristalle gestört würden.

Elektronik-Silizium ist normalerweise versetzungsfrei, unabhängig von den Züchtungsverfahren Zonen-Floating und Czochalski. Bei Germanium hängt die Versetzungsdichte sehr vom Verfahren ab, vor allem bei optischen Bauteilen für die Infrarot-Optik kann sie hoch sein, es wird aber auch versetzungsarmes bis versetzungsfreies Germanium gezüchtet. Bei Galliumarsenid (GaAs) hängt die Versetzungsdichte stark vom Züchtungsverfahren und der Dotierung ab. Züchtung mittels „Vertical Gradient Freezing“ (VGF) ermöglicht Versetzungsdichten zwischen 10 cm⁻² (Silizium-Dotierung) und 10³ cm⁻² (Undotiert). Mittels „Liquid encapsulated Czochalski“ (LEC) gezüchtete undotierte Kristalle von 150 mm Durchmesser weisen Versetzungsdichten im Bereich 10⁵ cm⁻² auf. Indium dotiertes Galliumarsenid (GaAs: In, ca. 0,1–1 % Indium) ist fast Versetzungsfrei. Andere Verbindungshalbleiter (InP, GaP, InAs) liegen in ähnlichem Bereich. Bei Versetzungsdichten oberhalb 10⁶ cm⁻², wird zumeist der Umschlag zu polykristallinem Wachstum beobachtet.

GaN und AlN weisen in den Initialphasen bei Heteroepitaxie auf Saphir oder Silizium Versetzungsdichten bis zu 10⁹ cm⁻² auf. Dann wird aber eine Schichtfolge gewählt, die sie drastisch absenkt, damit im aktiven Gebiet des Bauelementes Werte unter 10⁷ cm⁻², erreicht werden. Frei wachsende Kristalle haben wieder eine geringere Versetzungsdichte (AlN-Züchtung mittels Gasphasentransport ca. 10³ cm⁻², ).

Die Versetzungen kommen in Einkristallen vor allem durch thermische Spannungen beim Abkühlprozess in das Material, bei Halbleiterheteroschichtsystemen meist durch eine Gitterfehlanpassung. Möglichst versetzungsarme Einkristalle erhält man daher durch schonende Abkühlung.

Beispiel in 2 Dimensionen

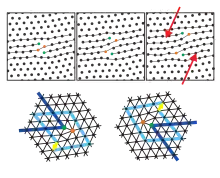
Bild 8. Dissoziation eines Dislokationspaares aufgrund von Scherung (rote Pfeile) eines hexagonalen Kristalls in 2D. Eine Dislokation besteht aus einem Paar von Teilchen mit fünffacher (grün) und siebenfacher (orange) Koordinationszahl.

In zwei Dimensionen existiert nur die Stufenversetzung, die eine zentrale Rolle beim Schmelzen in 2D hat, nicht jedoch die Schraubenversetzung.

Diese Dislokationen bilden topologische Punktdefekte, d. h. sie können einzeln nicht lokal durch eine affine Transformation erzeugt werden. Entstehen können sie nur paarweise mit antiparallelem Burgersvektor. Sind viele Dislokationen z. B. durch thermische Fluktuationen vorhanden, so wird die diskrete Translationsordnung des Kristalls zerstört, gleichzeitig verschwinden der Scher- und der Elastizitätsmodul, d. h. der Kristall ist zu einer flüssigen Phase geschmolzen. Die Orientierungsordnung ist jedoch noch nicht zerstört, und man findet – ähnlich wie bei Flüssigkristallen – eine anisotrope Phase mit typischerweise sechszähliger Richtungssymmetrie, hexatische Phase genannt. Erst die Anwesenheit von Disklinationen (Bild 8) erzeugt eine isotrope Flüssigkeit.[5][6] Dieser zweistufige Schmelzprozess mittels Dislokationen und Disklinationen wird in der KTHNY-Theorie beschrieben.

Versetzungen in triklinen Kristallen

Die Betrachtung von Versetzungen in einem Kristallgitter ohne rechte Winkel führt zu einer neuen Sichtweise und bietet die Möglichkeit genauer zu erkennen, welche Aussagen über Versetzungen allgemeingültig sind. Dies geschieht auf der Grundlage einer umfassenden Untersuchung der plastischen Deformation von Kristallen zweier isomorpher trikliner TCNQ-Komplexsalze als Modellkörper.[7] Es handelt sich um Molekülkristalle der Substanzen Triphenylmethylphosphonim-Bis-7.7.8.8. Tetracyanochinodimethanid (kurz: [Ph]) und Triphenylmethylarsonim-Bis-7.7.8.8. Tetracyanochinodimethanid (kurz: [As]), die wegen der außergewöhnlich starken Anisotropie ihrer elektrischen Leitfähigkeit interessant sind.[8]

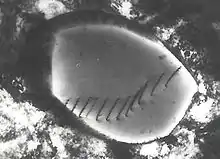
Durch Zufall wurde gefunden, dass die Eindrücke von Bronzedrähten, die als Messelektroden dienten, von Gleitstufen umgeben waren – ein sicheres Zeichen für plastische Deformation (Bild 9).

Bild 9. Gleitstufen in der Umgebung eines Elektrodeneindrucks auf (100)-Fläche von [As]

Bild 10. Triklines 2-D-Gitter mit Stufenversetzung

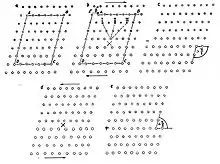
Wie die Entstehung einer Gleitstufe mit der Bewegung einer Versetzung zusammenhängt, lässt sich anhand der schematischen Darstellung der lokalen Verformung eines zweidimensionalen Gitters (Bild 10) zeigen. Bei Druck auf den oberen Teil des Gitters von links nach rechts wird dieser unter Bildung einer Gleitstufe von der Oberfläche her um g verschoben, wobei im Innern bei X eine Störung der Periodizität entsteht – eine Versetzung (b). Überträgt man den Umlauf ABCD aus dem ungestörten Gitter (a) in das gestörte Gitter, so benötigt man zum vollständigen Schließen des Umlaufs den Gittervektor b = g. Dabei ist b der Burgersvektor.

Bild 11. Elementare Gleitstufe

Wenn die Versetzung sich bis zum rechten Rand bewegt (c), ist die Abgleitung vollständig, und es entsteht auch dort eine Gleitstufe. Die Bewegung der Versetzung erfolgt dabei in der Gleitebene, an die sie gebunden ist. Nach einer vollständigen Abgleitung ist der Kristall versetzungsfrei.

Wird Druck auf den oberen Teil von rechts nach links ausgeübt, entsteht zuerst an der rechten Seite eine Gleitstufe und im Innern eine Versetzung (d). Nach vollständiger Abgleitung hat die Versetzung links den Kristall verlassen, und es entsteht auch dort eine Gleitstufe (e).

Weil es in dem Gitter keine rechten Winkel gibt, hat der Begriff Stufenversetzung hier nur Sinn als Rand einer zusätzlichen Gitterebene, und es haben die Stufen in (c) und (e) ein unterschiedliches Profil: bei (c) sind sie stumpfwinklig, bei (e) spitzwinklig.

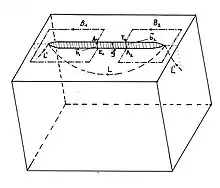
In der schematischen Darstellung einer elementaren Gleitstufe (Bild 11), die durch lokale Verschiebung eines Teils des Kristalls um den Gittervektor g (Gleitvektor) entstanden ist, lässt sich mit einem Burgers-Umlauf um die Endpunkte der Gleitstufe nachweisen, dass dort eine Versetzung mit dem Burgersvektor b = + g die Oberfläche schneidet und zugleich, dass sich dort das Zentrum eines schraubenartigen Zusammenhangs zwischen benachbarten Gitterebenen befindet. Diese Gitterstörung muss sich in das Kristallinnere längs einer Linie fortsetzen. Wie diese Linie verläuft, kann nicht gesagt werden. Beim Verlauf L begann die Verschiebung an der Oberfläche, und die Versetzung wanderte in den Kristall hinein. Beim Verlauf L' hat eine aus dem Innern des Kristalls kommende Versetzung die Oberfläche erreicht. Die Herstellung eines schraubenförmigen Zusammenhang von Gitterebenen erfordert nicht, dass die Versetzungslinie parallel zum Burgersvektor orientiert ist, wie durch die traditionelle Definition der Schraubenversetzung suggeriert.

Bild 12. Gleitstufen bei einem Nadeleinstich auf (100) von [As], TEM-Foto von Kohlenstoffabdruck.

Das TEM-Foto des Gleitstufenfeldes neben einem Nadeleinstich auf die (100)-Fläche eines [As]-Kristalls (Bild 12) lässt erkennen, dass bei der plastischen Deformation Mehrfach-Gleitstufen entstehen, bei denen Gleitung wiederholt in der gleichen Gleitebene aktiviert wird. Dies spricht für den Versetzungsverlauf längs L in Bild 11, denn es kann als unwahrscheinlich gelten, dass sich beim Kristallwachstum zufällig entstandene Versetzungen geordnet in der gleichen Gleitebene befinden

Bild 13. Stufenversetzung im triklinen Kristall projiziert auf die Gleitebene

Auch Stufenversetzungen erzeugen einen schraubenförmigen Zusammenhang zwischen benachbarten Gittereben, wenn diese von der Versetzungslinie geschnitten werden und nicht parallel zum Burgersvekror orientiert sind. Bild 13 zeigt diese Situation als Projektion einer Stufenversetzung auf die Gleitebene in der von Read praktizierten Zeichentechnik.[9] Die ausgefüllten Punkte liegen in Blickrichtung vor der Gleitebene, die offenen Kreise dahinter. Am rechten Rand der Grafik sieht man auf die Flanke einer Gleitstufe. Eingezeichnet sind zwei Burgersumläufe unterschiedlicher Orientierung, welche beide zum gleichen Burgersverktor b führen. Der schief zum Burgersvektor von links unten nach rechts oben geführte Umlauf führt in eine benachbarte Gitterebene und weist dabei auf einen von der Versetzung erzeugten schraubenartigen Zusammenhang hin.

Es gilt ganz allgemein: Jede Versetzung erzeugt einen schraubenartigen Zusammenhang zwischen Gitterebenen, die von ihr geschnitten werden und nicht parallel zum Burgersvektor orientiert sind.

Versetzungsnachweis durch Ätzung

Am Schnittpunkt einer Versetzung mit der Kristalloberfläche wird der Angriff eines Lösungsmittels begünstigt. Der Lösungsvorgang wird dabei längs der Versetzungslinie in die Tiefe geführt, wobei eine Ätzgrube entsteht mit einer den Ort der Versetzung markierenden Spitze. Dies kann zum Nachweis von Versetzungen und ihrer Verteilung auf der Kristalloberfläche benutzt werden.

Bild 14. Gleitstufen (a) und zugehörige Ätzgruben (b) in der Umgebung eines Mikrohärteeindrucks auf (100) von [As]

Bild 14 zeigt ein Beispiel. Hier wurde die Oberfläche des [As]-Kristalls durch das Lösungsmittel Acetonitril angelöst/geätzt. Um einen vergröbernden Anlösevorgang zu vermeiden, wurde dafür gesorgt, dass das Lösungsmittel nur sehr kurze Zeit (etwa 0,1 s) einwirken konnte. Gezeigt wird die Umgebung eines Mikrohärte-Eindrucks, im Bild 14 a das Gleitstufenfeld und in Bild 14 b das zugehörige Ätzbild. Die Ätzgruben markieren den Anfang jeder Gleitstufe und jeden Punkt, an dem die Gleitstufenhöhe durch wiederholte Benutzung der gleichen Gleitebene jeweils um einen Netzebenenabstand (hier 1,5 nm) wächst oder abnimmt. Durch einen Pfeil wird in (a) der Beginn der Sichtbarkeit einer Gleitstufe markiert, in (b) an der gleichen Stelle die dritte Ätzgrube. Die Sichtbarkeit der Gleitstufe im Auflichtmikroskop bei schiefer Beleuchtung begann also bei einer Stufenhöhe von 4,5 nm. Die Reihung zahlreicher Ätzgruben längs der Gleitstufen zeigt, dass die vielfache Benutzung identischer Gleitebenen durch nacheinander bei fortdauernder Belastung erzeugte Versetzungen der Regelfall ist.

Bild 15. Schema einer Vierfach-Gleitstufe

Die schematische Darstellung einer Vierfach-Gleitstufe (Bild 15) zeigt, wie die Versetzungen einen schraubenförmigen Zusammenhang zwischen den von ihnen geschnittenen Gitterebenen herstellen. In dem am weitesten von der Oberfläche entfernten Abschnitt verlaufen die Versetzungen parallel zu den Gitterebenen und erzeugen dort keinen schraubenförmigen Zusammenhang. Sie haben dort die Orientierung einer Stufenversetzung.

Siehe auch

Literatur

J. M. Burgers: Some considerations on the fields of stress connected with dislocations in a regular crystal lattice. In: Proceedings of the Section of Sciences. Koninklijke Nederlandse Akademie van Wetenschappen. Bd. 42, 1939, ISSN 0370-0348, S. 293–325, 378–399.
Jacques Friedel: Les dislocations. Gauthier Villars, Paris, 1956 (2nd ed. Pergamon, Dislocations 1964).
Derek Hull, David J. Bacon: Introduction to Dislocations (= International Series on Materials Science and Technology. Bd. 37). 3rd edition. Pergamon Press, Oxford u. a. 1984, ISBN 0-08-028720-4.
John P. Hirth, Jens Lothe: Theory of dislocations. 2nd edition. Wiley, New York NY u. a. 1982, ISBN 0-471-09125-1.
Hagen Kleinert: Gauge Fields in Condensed Matter. Disorder Fields and Applications to Superfluid Phase Transition and Crystal Melting. Volume 2: Stresses and Defects. Differential Geometry, Crystal Melting. World Scientific, Singapur u. a. 1989, ISBN 9971-5-0210-0, S. 743–1456 (online lesbar auf den Seiten des Autors).
R. Fornari (Hrsg.): Single crystals in electronic materials. Elsevier Ltd, 2019, ISBN 978-0-08-102096-8.
Peter Haasen: Physikalische Metallkunde. 3., neubearbeitete und erw. Aufl. Berlin/Heidelberg, ISBN 978-3-642-87849-7.

Weblinks

Wikibooks: Werkstoffkunde Metall – Lern- und Lehrmaterialien

Physikalische Werkstoffeigenschaften (Ausführliches Vorlesungsskript TU Dresden)

Einzelnachweise

Christoph Broeckmann, Paul Beiss: Werkstoffkunde I. Institut für Werkstoffanwendungen im Maschinenbau der RWTH Aachen, Aachen 2014, S. 162–182.
E. Orowan: Zur Kristallplastizität. I. In: Zeitschrift für Physik. Band 89, Nr. 9, 1. September 1934, S. 605–613, doi:10.1007/BF01341478.
E. Orowan: Zur Kristallplastizität. II. In: Zeitschrift für Physik. Band 89, Nr. 9, September 1934, S. 614–633, doi:10.1007/BF01341479.
E. Orowan: Zur Kristallplastizität. III. In: Zeitschrift für Physik. Band 89, Nr. 9, September 1934, S. 634–659, doi:10.1007/BF01341480.
M. Polanyi: Über eine Art Gitterstörung, die einen Kristall plastisch machen könnte. In: Zeitschrift für Physik. Band 89, Nr. 9, September 1934, S. 660–664, doi:10.1007/BF01341481.
Geoffrey Ingram Taylor: The mechanism of plastic deformation of crystals. Part I.—Theoretical. In: Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. Band 145, Nr. 855, 2. Juli 1934, S. 362–387, doi:10.1098/rspa.1934.0106.
Geoffrey Ingram Taylor: The mechanism of plastic deformation of crystals. Part II.—Comparison with observations. In: Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. Band 145, Nr. 855, 2. Juli 1934, S. 388–404, doi:10.1098/rspa.1934.0107.
Urs Gasser, Christoph Eisenmann, Georg Maret, Peter Keim: Melting of Crystals in Two Dimensions. In: ChemPhysChem. Band 11, Nr. 5, 2010, S. 963–970, doi:10.1002/cphc.200900755.
Urs Gasser, Georg Maret, Peter Keim: Das Schmelzen zweidimensionaler Kristalle. Phasenübergänge durch topologische Defekte. In: Physik in unserer Zeit. Band 39, Nr. 1, 2008, S. 36–43, doi:10.1002/piuz.200601138.
Heinz H. W. Preuß: Trikline TCNQ-Komplexsalze als Modellkörper zur Untersuchung der Kristallplastizität bei niederer Symmetrie, Dissertation B (Habilitationsschrift), Leipzig 1977. In: Der Rektor der Bergakademie Freiberg (Hrsg.): Freiberger Forschungsheft. B 204. VEB Deutscher Verlag für Grundstoffindustrie, Leipzig 1978.
E. Müller, H. Ritschel, H. Hänsel: The Anisotropy of Electrical Conductivity and Thermoelectric Power in Single Crystals of the Anion Radical Salt [(C6H5)3 AsCH3]+ TCNQ2−. In: physica status solidi (b). Band 33, Nr. 1, 1969, S. K55–K58, doi:10.1002/pssb.19690330168.
W. T. Read (Jr.): Dislocations in Crystals. London 1953.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[broeckmann-1] Christoph Broeckmann, Paul Beiss: Werkstoffkunde I. Institut für Werkstoffanwendungen im Maschinenbau der RWTH Aachen, Aachen 2014, S. 162–182.

[2] E. Orowan: Zur Kristallplastizität. I. In: Zeitschrift für Physik. Band 89, Nr. 9, 1. September 1934, S. 605–613, doi:10.1007/BF01341478.
E. Orowan: Zur Kristallplastizität. II. In: Zeitschrift für Physik. Band 89, Nr. 9, September 1934, S. 614–633, doi:10.1007/BF01341479.
E. Orowan: Zur Kristallplastizität. III. In: Zeitschrift für Physik. Band 89, Nr. 9, September 1934, S. 634–659, doi:10.1007/BF01341480.

[3] M. Polanyi: Über eine Art Gitterstörung, die einen Kristall plastisch machen könnte. In: Zeitschrift für Physik. Band 89, Nr. 9, September 1934, S. 660–664, doi:10.1007/BF01341481.

[4] Geoffrey Ingram Taylor: The mechanism of plastic deformation of crystals. Part I.—Theoretical. In: Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. Band 145, Nr. 855, 2. Juli 1934, S. 362–387, doi:10.1098/rspa.1934.0106.
Geoffrey Ingram Taylor: The mechanism of plastic deformation of crystals. Part II.—Comparison with observations. In: Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. Band 145, Nr. 855, 2. Juli 1934, S. 388–404, doi:10.1098/rspa.1934.0107.

[5] Urs Gasser, Christoph Eisenmann, Georg Maret, Peter Keim: Melting of Crystals in Two Dimensions. In: ChemPhysChem. Band 11, Nr. 5, 2010, S. 963–970, doi:10.1002/cphc.200900755.

[6] Urs Gasser, Georg Maret, Peter Keim: Das Schmelzen zweidimensionaler Kristalle. Phasenübergänge durch topologische Defekte. In: Physik in unserer Zeit. Band 39, Nr. 1, 2008, S. 36–43, doi:10.1002/piuz.200601138.

[7] Heinz H. W. Preuß: Trikline TCNQ-Komplexsalze als Modellkörper zur Untersuchung der Kristallplastizität bei niederer Symmetrie, Dissertation B (Habilitationsschrift), Leipzig 1977. In: Der Rektor der Bergakademie Freiberg (Hrsg.): Freiberger Forschungsheft. B 204. VEB Deutscher Verlag für Grundstoffindustrie, Leipzig 1978.

[8] E. Müller, H. Ritschel, H. Hänsel: The Anisotropy of Electrical Conductivity and Thermoelectric Power in Single Crystals of the Anion Radical Salt [(C6H5)3 AsCH3]+ TCNQ2−. In: physica status solidi (b). Band 33, Nr. 1, 1969, S. K55–K58, doi:10.1002/pssb.19690330168.

[9] W. T. Read (Jr.): Dislocations in Crystals. London 1953.