Kristallmorphologie
Die Kristallmorphologie ist ein Begriff aus der Kristallographie und der Mineralogie und beschreibt die Form eines Kristalls, der aus geometrisch bestimmten Flächen, Kanten und Ecken besteht. Zwei aneinander stoßende Kristallflächen bilden dabei eine Kristallkante und mindestens drei Kanten bilden eine Kristallecke. Je nach Kristallsystem und Kristallklasse schließen die Kanten dabei bestimmte, für die betreffende Kristallklasse charakteristische Winkel ein.
Um die Lage von Kristallflächen und -kanten im Raum mathematisch zu beschreiben, bedient sich der Mineraloge verschiedener Indizes. Mit den Millerschen Indizes (hkl) wird dabei die Lage der Flächen in Bezug auf das Achsensystem des Kristalls beschrieben, mit den Richtungsindizes [uvw] die Richtung der Kanten.
Kristallfläche
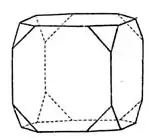
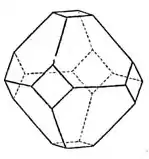
Die Kristallflächen bilden die äußere Begrenzung des Kristallkörpers und liegen parallel zu den Gitter- beziehungsweise Netzebenen der dem Kristall innewohnenden Kristallstruktur, die wiederum von seiner chemischen Zusammensetzung abhängt. Durch Symmetrieoperationen ineinander überführbare kristallographische Flächen heißen Form (siehe unten: Abschnitt Kristallform). Die Kombination der ausgebildeten Formen heißt Tracht. Dieser Begriff ist nicht zu verwechseln mit dem Habitus, der die geometrische Ausdehnung eines Kristalls beschreibt. Der Habitus kann z. B. stängelig, faserig, plattig oder isometrisch sein.
Kristallflächen bilden sich bevorzugt an den Netzebenen, die die dichteste Packung (größte Anzahl von Atomen) und gleichzeitig möglichst wenig freie, offene Valenzen aufweisen (chemische Neutralität). Bei idealen Kristallen besitzen die Flächen eine klare Geometrie (Dreieck, Viereck, Sechseck) und bilden zusammen regelmäßige Körper (siehe platonischer Körper, catalanischer Körper). Bei Kristallen, die ihre Eigengestalt störungsfrei voll entwickeln konnten, spricht man auch von idiomorphen Kristallen. Welche Gestalt dies ist, bestimmt die jeweilige Kristallklasse, der der Kristall angehört. Ein idiomorpher Kristall ist daher nicht gleichzusetzen mit einem holoedrischen Kristall.
Natürliche Kristalle bilden sich aber nur selten in der idealen Form, bedingt durch Störungen der Stoffzufuhr und das anisotrope Verhalten beim Wachsen des Kristalls während der Kristallisation oder durch gegenseitige Behinderung bei einer Vielzahl gleichzeitig entstehender Kristalle, beispielsweise bei schneller Abkühlung. Kristallflächen können somit verzerrt sein oder sogar ganz fehlen. Sie stehen jedoch zum einen immer konvex zueinander, was bedeutet, dass sie sich vom Kristallmittelpunkt „wegbeugen“ und zum anderen bleiben trotz aller Verformungen die Winkel zwischen den Flächen immer konstant. Bei Kristallen, die ihre Eigengestalt aufgrund der genannten Störungen nur teilweise entwickeln konnten, spricht man von hypidiomorphen Kristallen.
Wird ein Kristall während des Wachstums so sehr gestört, dass er seine Eigengestalt gar nicht entwickeln konnte, spricht man von xenomorphen Kristallen.
Kristallform
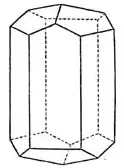
In der Kristallographie bezeichnet man als Form (seltener Kristallform oder Flächenform; engl. form, crystal form, face form, frz. forme[1]) die Gesamtheit aller zueinander symmetrieäquivalenten Kristallflächen. Eine Kristallform wird mit dem Symbol {hkl}, also den millerschen Indizes (hkl) einer der Flächen in geschweiften Klammern, bezeichnet. Man beachte, dass sich die kristallographische Bedeutung des Begriffs Kristallform deutlich von der umgangssprachlichen Bedeutung unterscheidet: die „Form“ eines Kristalls im umgangssprachlichen Sinn wird eher durch die Begriffe Tracht und Habitus beschrieben. Ein einzelner Kristall hat genau eine Tracht und einen Habitus, aber in der Regel mehrere (kristallographische) Formen. Weiterhin ist zu beachten, dass mit dem Begriff Kristallform insbesondere in der Kristallographie organischer Molekülverbindungen und biologischer Makromoleküle häufig eine Modifikation im Sinne der Polymorphie bezeichnet wird, die sich in der Packung der Moleküle und damit in der Regel in der Raumgruppe und den Gitterparametern von anderen Kristallformen unterscheidet.
Kristallformen können geschlossene Körper (Polyeder), wie Würfel oder Oktaeder, bilden. Daneben gibt es aber auch offene Formen, wie das Pinakoid, aber auch Prismen und Pyramiden. Solche offenen Formen müssen an einem Kristall notwendig mit anderen Formen kombiniert sein. Man beachte, dass die Basisflächen von Prismen oder Pyramiden – anders als in der Schulgeometrie – nicht zur Form dazugehören; sie sind nicht symmetrieäquivalent zu den eigentlichen Prismen- oder Pyramidenflächen. Ein tetragonales (quadratisches) Prisma hat in der Kristallographie also vier, nicht sechs Flächen.
Insgesamt gibt es 17 offene (18, wenn man das Dieder in Doma und Sphenoid unterteilt) und 30 geschlossene Sorten kristallographischer Formen.[2][1]
Man unterscheidet daneben allgemeine Formen und spezielle Formen, außerdem Grenzformen. Die allgemeine Form {hkl} geht aus einer „Fläche allgemeiner Lage“ (hkl) hervor, das heißt die Fläche liegt nicht parallel oder senkrecht zu einer Spiegelebene oder senkrecht zu einer Drehachse; die Indizes h, k, l sind im Allgemeinen nicht null und paarweise verschieden. Andernfalls handelt es sich um spezielle Formen. Grenzformen nehmen eine Zwischenstellung ein: Sie haben die gleiche Flächenzahl und Symmetrie wie die allgemeine Form. Zum Beispiel ist die allgemeine Form der Kristallklasse 3 die trigonale Pyramide {hkil}; wird der Index l immer kleiner, die Flächen also immer steiler, so ergibt sich als Grenzform das trigonale Prisma {hki0}. Eine spezielle Form in dieser Kristallklasse wäre die Basisfläche (das Pedion) (0001).
Die folgenden Tabellen geben einen Überblick über alle Formen der 32 Kristallklassen. Nebeneinander stehen zunächst die allgemeine Form {hkl}, dann die speziellen und Grenzformen. Angegeben ist jeweils der Name der Form mit Synonymen sowie die Zahl der Flächen.
| Kristallklasse | {hkl} | |
|---|---|---|
| triklin-pedial | Pedion (1) | |
| triklin-pinakoidal | Pinakoid (2) | |
| Kristallklasse | {hkl} | {h0l} | {010} | |
|---|---|---|---|---|
| monoklin-sphenoidisch | Sphenoid (2) |
(Klino-) Pinakoid (2) | Pedion (1) | |
| monoklin-domatisch | Doma (2) |
Pedion (1) | (Ortho-) Pinakoid (2) | |
| monoklin-prismatisch | monoklines Prisma (4) | (Klino-) Pinakoid (2) | (Ortho-) Pinakoid (2) | |
| Kristallklasse | {hkl} | {hk0} | {h0l} und {0hl} | {100} und {010} | {001} | |
|---|---|---|---|---|---|---|
| rhombisch-pyramidal | rhombische Pyramide (4) |
rhombisches Prisma (4) |
Doma (2) | Pinakoid (2) | Pedion (1) | |
| rhombisch-disphenoidisch | rhombisches Disphenoid (4) |
rhombisches Prisma (4) |
rhombisches Prisma (4) |
Pinakoid (2) | ||
| rhombisch-dipyramidal | rhombische Dipyramide (8) |
rhombisches Prisma (4) |
rhombisches Prisma (4) |
Pinakoid (2) | ||
| Kristallklasse | {hkl} | {h0l} | {hhl} | {hk0} | {100} und {110} | {001} | |
|---|---|---|---|---|---|---|---|
| tetragonal-pyramidal | tetragonale Pyramide (4) |
tetragonales Prisma (4) |
Pedion (1) | ||||
| tetragonal-disphenoidisch | tetragonales Disphenoid (4) |
tetragonales Prisma (4) |
Pinakoid (2) | ||||
| tetragonal-dipyramidal | tetragonale Dipyramide (8) |
tetragonales Prisma (4) |
Pinakoid (2) | ||||
| ditetragonal-pyramidal | ditetragonale Pyramide (8) |
tetragonale Pyramide (4) |
ditetragonales Prisma (8) |
tetragonales Prisma (4) |
Pedion (1) | ||
| tetragonal-skalenoedrisch | tetragonales Skalenoeder (8) |
tetragonale Dipyramide (8) |
tetragonales Disphenoid (4) |
ditetragonales Prisma (8) |
tetragonales Prisma (4) |
Pinakoid (2) | |
| tetragonal-trapezoedrisch | tetragonales Trapezoeder (8) |
tetragonale Dipyramide (8) |
ditetragonales Prisma (8) |
tetragonales Prisma (4) |
Pinakoid (2) | ||
| ditetragonal-dipyramidal | ditetragonale Dipyramide (16) |
tetragonale Dipyramide (8) |
ditetragonales Prisma (8) |
tetragonales Prisma (4) |
Pinakoid (2) | ||
| Kristallklasse | {hkil} | {h0hl} | {hh 2h l} | {hki0} | {1010} | {1120} | {0001} | |
|---|---|---|---|---|---|---|---|---|
| trigonal-pyramidal | trigonale Pyramide (3) |
trigonales Prisma (3) |
Pedion (1) | |||||
| rhomboedrisch | 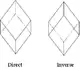 Rhomboeder (6) |
hexagonales Prisma (6) |
Pinakoid (2) | |||||
| ditrigonal-pyramidal | ditrigonale Pyramide (6) |
trigonale Pyramide (3) |
hexagonale Pyramide (6) |
ditrigonales Prisma (6) |
trigonales Prisma (3) |
hexagonales Prisma (6) |
Pedion (1) | |
| trigonal-trapezoedrisch | trigonales Trapezoeder (6) |
 Rhomboeder (6) |
trigonale Dipyramide (6) |
ditrigonales Prisma (6) |
hexagonales Prisma (6) |
trigonales Prisma (3) |
Pinakoid (2) | |
| ditrigonal-skalenoedrisch | ditrigonales Skalenoeder (12) |
 Rhomboeder (6) |
hexagonale Diyramide (12) |
dihexagonales Prisma (12) |
hexagonales Prisma (6) |
Pinakoid (2) | ||
| Kristallklasse | {hkil} | {h0hl} | {hh 2h l} | {hki0} | {1010} | {1120} | {0001} | |
|---|---|---|---|---|---|---|---|---|
| hexagonal-pyramidal | hexagonale Pyramide (6) |
hexagonales Prisma (6) |
Pedion (1) | |||||
| trigonal-dipyramidal | trigonale Dipyramide (6) |
trigonales Prisma (3) |
Pinakoid (2) | |||||
| hexagonal-dipyramidal | hexagonale Dipyramide (12) |
hexagonales Prisma (6) |
Pinakoid (2) | |||||
| dihexagonal-pyramidal | dihexagonale Pyramide (12) |
hexagonale Pyramide (6) |
dihexagonales Prisma (12) |
hexagonales Prisma (6) |
Pedion (1) | |||
| ditrigonal-dipyramidal | ditrigonale Dipyramide (12) |
trigonale Dipyramide (6) |
hexagonale Diyramide (12) |
ditrigonales Prisma (6) |
trigonales Prisma (3) |
hexagonales Prisma (6) |
Pinakoid (2) | |
| hexagonal-trapezoedrisch | hexagonales Trapezoeder (12) |
hexagonale Dipyramide (12) |
dihexagonales Prisma (12) |
hexagonales Prisma (6) |
Pinakoid (2) | |||
| dihexagonal-dipyramidal | dihexagonale Dipyramide (24) |
hexagonale Dipyramide (12) |
dihexagonales Prisma (12) |
hexagonales Prisma (6) |
Pinakoid (2) | |||
| Kristallklasse | {hkl} | {hhl} (h>l) | {hll} (h>l) | {hk0} | {111} | {110} | {100} | |
|---|---|---|---|---|---|---|---|---|
| tetraedrisch-pentagondodekaedrisch | tetraedrisches Pentagondodekaeder (Pentagon-Tritetraeder, Tetartoeder) (12) |
Deltoiddodekaeder (Tetragon-Tritetraeder) (12) |
Triakistetraeder (Tristetraeder, Trigon-Tritetraeder) (12) |
Pentagondodekaeder (Pyritoeder) (12) |
Tetraeder (4) |
Rhombendodekaeder (Granatoeder) (12) |
Würfel (Hexaeder) (6) | |
| disdodekaedrisch | Disdodekaeder (Dyakisdodekaeder, Diploeder, Diploid) (24) |
Triakisoktaeder (Trisoktaeder, Trigon-Trioktaeder) (24) |
Deltoidikositetraeder (Ikositetraeder, Tetragon-Trioktaeder, Trapezoeder, Leucitoeder) (24) |
Pentagondodekaeder (Pyritoeder) (12) |
Oktaeder (8) |
Rhombendodekaeder (Granatoeder) (12) |
Würfel (Hexaeder) (6) | |
| pentagonikositetraedrisch | Pentagonikositetraeder (Gyroeder, Gyroid) (24) |
Triakisoktaeder (...) (24) |
Deltoidikositetraeder (...) (24) |
Tetrakishexaeder (Tetrahexaeder) (24) |
Oktaeder (8) |
Rhombendodekaeder (Granatoeder) (12) |
Würfel (Hexaeder) (6) | |
| hexakistetraedrisch | Hexakistetraeder (Hexatetraeder) (24) |
Deltoiddodekaeder (Tetragon-Tritetraeder) (12) |
Triakistetraeder (...) (12) |
Tetrakishexaeder (Tetrahexaeder) (24) |
Tetraeder (4) |
Rhombendodekaeder (Granatoeder) (12) |
Würfel (Hexaeder) (6) | |
| hexakisoktaedrisch | Hexakisoktaeder (Hexaoktaeder) (48) |
Triakisoktaeder (...) (24) |
Deltoidikositetraeder (...) (24) |
Tetrakishexaeder (Tetrahexaeder) (24) |
Oktaeder (8) |
Rhombendodekaeder (Granatoeder) (12) |
Würfel (Hexaeder) (6) | |
Morphologische Gesetze
Das Gesetz der Winkelkonstanz
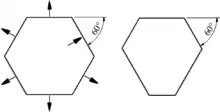
Das Gesetz der Winkelkonstanz besagt:
Alle zur selben Kristallart gehörenden Einzelkristalle schließen zwischen analogen Flächen – gleichen Druck, gleiche Temperatur und chemische Zusammensetzung vorausgesetzt – stets gleiche Winkel ein.
Der Däne Niels Stensen (lat. Nicolaus Steno) bemerkte um 1669 bei der Untersuchung von Quarz, dass die Flächen der Kristalle – unabhängig von ihrer Größe und Form – immer gleiche Winkel bilden. Er vermutete, dass dies eine Eigenschaft aller Mineralkristalle sei.[3] Bestätigt wurde diese Vermutung nach weiteren Vorarbeiten durch Torbern Olof Bergman schließlich von Jean-Baptiste Romé de L’Isle. Romé de L’Isle und sein Assistent Arnould Carangeot vermaßen systematisch Kristalle mit dem von Carangeot entwickelten Anlegegoniometer. 1783 veröffentlichte Romé de L’Isle eine detaillierte Beschreibung von 500 Kristallarten, die auf diesen Messungen basierte.[4] Dabei konnte er empirisch bestätigen, dass das Gesetz der Winkelkonstanz – wie von Steno vermutet – für jede Kristallart gilt. Romé de L’Isles systematische Messungen und der daraus folgende induktive Beweis des Gesetzes der Winkelkonstanz sind das erste Beispiel für wissenschaftliches (methodisch-empirisches) Vorgehen in der Kristallographie. Insofern kann Romé de L’Isle als Begründer der wissenschaftlichen Kristallographie gelten.
Wenn man bedenkt, auf welche Weise Kristalle wachsen, ist dieses Gesetz nur logisch. Die chemische Zusammensetzung und die Bindungsart der Grundbausteine eines Minerals bestimmt die Ausbildung des Kristallsystems mit den entsprechenden Atomen und Molekülen an den Kreuzungspunkten des Raumgitters. Weitere Atome werden immer parallel zu den einzelnen Ebenen des Raumgitters eingebaut. Durch Konvektionsströme innerhalb der mineralischen Lösung kommt es zur unregelmäßigen Verteilung der aufbauenden Atome und damit zur Bevorzugung oder Benachteiligung einzelner Flächen. Dennoch bleiben die Winkel zwischen den Ebenen des Raumgitters durch das vorbestimmte Kristallsystem zwingend erhalten.
Das Rationalitätsgesetz
Das Rationalitätsgesetz (auch Rationalitätsprinzip, Gesetz der rationalen Verhältnisse oder Gesetz der rationalen Indizes) besagt, dass sich alle Kristallflächen und alle Kanten durch rationale Indizes darstellen lassen. Die Indizes sind immer kleine ganze Zahlen. Das gilt sowohl für die Weiss'schen Indizes m:n:p als auch für deren Kehrwerte, die später eingeführten Millerschen Indizes (hkl). Das Rationalitätsgesetz in dieser Formulierung wurde 1809 von Christian Samuel Weiss eingeführt.[5]
Im Ansatz findet sich dieses Gesetz bereits im Dekreszenzgesetz („loi de décrescence“) von René-Just Haüy (1801). Es besagt: Bei der sukzessiven Aufschichtung der kleinsten Baueinheiten tritt jede folgende Schicht, bzw. eine Stufe aus m Schichten parallel einer Kante oder Flächendiagonale um eine feste Anzahl von n = 1, 2, 3, 6 Reihen subtraktiver Moleküle zurück.[6] Haüy bemerkte selbst, dass es unmöglich ist, das reguläre Dodekaeder aus würfelförmigen Baueinheiten zu erzeugen. Er berechnete für das reguläre Dodekaeder ein irrationales Verhältnis entsprechend dem Goldenen Schnitt.
Das Bravaissche Gesetz
Mit Auguste Bravais begannen Versuche, Gesetze zu finden, mit denen sich die Kristallmorphologie aus der inneren Kristallstruktur vorhersagen lässt (und umgekehrt). Bravais sagte um 1848 voraus, dass die „relative Wichtigkeit“ einer Kristallfläche proportional ist zu ihrer Besetzungsdichte, das heißt, dass Formen umso wahrscheinlicher am Kristall auftreten, je mehr Gitterpunkte je Flächeneinheit auf der entsprechenden Gitterebene liegen. Gleichbedeutend damit ist, dass die morphologische Wichtigkeit einer Fläche umgekehrt proportional zum Netzebenenabstand ist.
Donnay-Harker-Regel
Im 20. Jahrhundert wurde das Bravaissche Gesetz (auch Bravaissches Prinzip, frz. „loi de Bravais“, engl. „Bravais rule“) von Georges Friedel[7] sowie von Joseph D. H. Donnay und David Harker[8] wieder aufgegriffen. Während Bravais bei seinen Überlegungen nur Zentrierungen (die Bravais-Gitter) berücksichtigte, bezogen Donnay und Harker auch andere Symmetrieelemente (Gleitspiegelebenen und Schraubenachsen) ein, die zu veränderten Besetzungsdichten von Gitterebenen führen. Sie konnten so jeder Raumgruppen eine Flächenrangfolge zuordnen, die sie morphologischer Aspekt nannten.
Die Goldschmidtsche Komplikationsregel
Victor Mordechai Goldschmidt stellte 1897 das Komplikationsgesetz (Komplikationsregel) auf, welches besagt, dass sich aus zwei Kristallflächen, z. B. (100) und (010), durch wiederholte Addition oder Subtraktion ihrer millerschen Indizes alle weiteren Flächen dieser Zone ableiten lassen. Durch umfangreiche statistische Untersuchungen konnte Goldschmidt zeigen, dass Flächen im Allgemeinen umso seltener auftreten, je „komplizierter“ diese Ableitung ist, also je größer ihre Indizes werden.[9]
Periodic Bond Chain
Die Periodic-Bond-Chain-Theorie oder Hartman-Perdok-Theorie leitet die Kristallmorphologie von den intermolekularen Bindungen zwischen den Kristallbausteinen ab. Diese Theorie wurde ab 1955 von Hartman und Perdok eingeführt.
Literatur
- Paul Ramdohr, Hugo Strunz: Lehrbuch der Mineralogie (16. Aufl.), Ferdinand Enke Verlag (1978), ISBN 3-432-82986-8
- Hans-Joachim Bautsch, Will Kleber, Joachim Bohm: Einführung in die Kristallographie. Oldenbourg Wissenschaftsverlag, 1998 (eingeschränkte Vorschau in der Google-Buchsuche).
Einzelnachweise
- IUCr Online Dictionary of Crystallographie: Form.
- Paul Niggli: Zur Topologie, Metrik und Symmetrie der einfachen Kristallformen. Schweiz. Mineral. u. Petrogr. Mitt. 43 (1963) S. 49–58.
- Nicolaus Steno: De solido intra solidum naturaliter contento dissertationis prodromus. (Vorläufer einer Dissertation über feste Körper, die innerhalb anderer fester Körper von Natur aus eingeschlossen sind.) Florenz 1669.
- Jean-Baptiste Romé de L’Isle: Cristallographie, ou Déscription des formes propres à tous les corps du règne minéral. 1783.
- C. S. Weiss: De indagando formarum crystallinarum charactere geometrico principali dissertatio. Lipsiae [Leipzig] 1809.
- René-Just Haüy: Traité de mineralogie etc. Tome 1–5. Paris 1801. / Dt.: Lehrbuch der Mineralogie etc. Paris und Leipzig 1804-10, Band 1, S. 34ff.
- Georges Friedel: Études sur la loi de Bravais. Bull. Soc. Franc. Miner. 30 (1907), S. 326–455.
- J. D. H. Donnay, David Harker: A new law of crystal morphology extending the law of Bravais. Amer. Miner. 22 (1937), S. 446.
- Victor Mordechai Goldschmidt: Über Entwicklung der Krystallformen. Z. Kristall. 28 (1897), S. 1–35, 414–451.