Orthorhombisches Kristallsystem

Das orthorhombische Kristallsystem gehört zu den sieben Kristallsystemen in der Kristallographie. Es umfasst alle Punktgruppen mit drei senkrecht aufeinander stehenden zweizähligen Dreh- oder Drehinversionsachsen. Das orthorhombische Kristallsystem wird auch rhombisches Kristallsystem genannt. Der Begriff rhombisch darf allerdings nicht mit rhomboedrisch verwechselt werden.

Brookit aus Pakistan

Hemimorphit

Punktgruppen

Das orthorhombische Kristallsystem umfasst die Punktgruppen $\ 222,\,mm2$ und $\ mmm$ . Sie bilden die orthorhombische Kristallfamilie und können mit dem orthorhombischen Gittersystem beschrieben werden.

Gittersystem

Das orthorhombische Gittersystem hat die Holoedrie $\ mmm$ .

Im orthorhombischen Gittersystem liegen Gitterachsen in Richtung der 3 senkrecht aufeinander stehenden Symmetrieachsen. Für die Länge der Gitterachsen erhält man keine weiteren Bedingungen. Somit ergibt sich:

a\neq b\neq c

\alpha =\beta =\gamma =90^{\circ }

Für die Festlegung, welche Achse a, b oder c ist, gibt es nur die Bedingung, dass ein rechtshändiges Koordinatensystem entstehen soll. In der Regel werden die Achsen so gewählt, dass das Hermann-Mauguin-Symbol dem Standard der International Tables for Crystallography entspricht. Mit den Hermann-Mauguin-Symbolen lassen sich die Raumgruppen allerdings bezüglich jeder möglichen Achsenwahl beschreiben. Da dies auch häufiger vorkommt, gibt es in den International Tables eine tabellarische Übersicht über alle Möglichkeiten, eine Raumgruppe mit einer beliebigen Achsenwahl zu beschreiben. Grundsätzlich empfiehlt es sich daher bei der Angabe der Raumgruppe, die Raumgruppennummer mitzuverwenden, da sie damit leichter zu finden ist.

Bravaisgitter

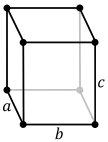Orthorhombisch primitives Gitter: oP
Orthorhombisch basiszentriertes Gitter: oC, oA (oB,oS)
Orthorhombisch innenzentriertes Gitter: oI
Orthorhombisch flächenzentriertes Gitter: oF

Im orthorhombischen Kristallsystem gibt es vier Bravaisgitter. In der Standardaufstellung kommt das b-zentrierte Gitter nicht und das a-zentrierte Gitter nur in der Punktgruppe $\ mm2$ vor. Dies ist dadurch begründet, dass in dieser Punktgruppe das Gittersystem grundsätzlich so aufgestellt wird, dass die zweizählige Achse in Richtung der c-Gitterachse liegt. Daher gelingt es nicht in allen Fällen die Gitterachsen so zu legen, dass ausschließlich das c-zentrierte Gitter verwendet wird. Das orthorhombische Gittersystem wird mit o abgekürzt.

Punktgruppen im orthorhombischen Kristallsystem und ihre physikalischen Eigenschaften

Zur Beschreibung der orthorhombischen Kristallklassen in Hermann-Mauguin-Symbolik werden die Symmetrieoperationen bezüglich drei vorgegebener Richtungen (Blickrichtungen) im Gittersystem angegeben. Wie im monoklinen entsprechen die 3 Blickrichtungen der a (<100>), b (<010>) und c Gitterachse (<001>). Da hier alle drei Gitterrichtungen Symmetrierichtungen sind, besteht allerdings auch das Hermann-Mauguin-Kurzsymbol aus drei Angaben.

Charakteristisch für die orthorhombischen Raumgruppen ist, dass im Hermann-Mauguin-Kurzsymbol keine 3, 4 oder 6 vorkommt.

Punktgruppe (Kristallklasse)								Physikalische Eigenschaften[Anm. 1]				Beispiele
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Internationales Symbol (Hermann-Mauguin)		Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Voll	Kurz	Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
6	orthorhombisch	orthorhombisch-disphenoidisch	D₂ (V)	222	222	mmm	16–24	+	+	–	+	Austinit Epsomit
7		orthorhombisch-pyramidal	C_2v	mm2	mm2		25–46	–	+	+ [001]	+	Hemimorphit Struvit
8		orthorhombisch-dipyramidal	D_2h (V_h)	2/m2/m2/m	mmm		47–74	–	–	–	–	Topas Anhydrit
Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist. Für die Pyroelektrizität ist, sofern vorhanden, auch die Richtung des pyroelektrischen Vektors angegeben.

Siehe auch

Für weitere orthorhombisch kristallisierende chemische Stoffe siehe Kategorie:Orthorhombisches Kristallsystem.
Orthotropie mit der kontinuumsmechanischen Beschreibung der Materialeigenschaften.

Literatur

Theo Hahn (Hrsg.): International Tables for Crystallography Vol. A D. Reidel publishing Company, Dordrecht 1983, ISBN 90-277-1445-2.
D. Schwarzenbach Kristallographie Springer Verlag, Berlin 2001, ISBN 3-540-67114-5.
Will Kleber, Hans-Joachim Bautsch, Joachim Bohm, Detlef Klimm: Einführung in die Kristallographie. 19. Auflage. Oldenbourg Wissenschaftsverlag, 2010, ISBN 978-3-486-59075-3.
Walter Borchard-Ott Kristallographie 7. Auflage Springer Verlag, Berlin 2009, ISBN 978-3-540-78270-4.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Hinweise-1] Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist. Für die Pyroelektrizität ist, sofern vorhanden, auch die Richtung des pyroelektrischen Vektors angegeben.