Schwerefeld

Ein Schwerefeld ist ein Kraftfeld, verursacht durch Gravitation und gegebenenfalls bestimmte Trägheitskräfte. Die Feldstärke des Schwerefeldes ist die Schwere, Formelzeichen ${\vec {g}}$ . Als auf die Masse bezogene Gewichtskraft eines Probekörpers hat sie die SI-Einheit N/kg = m/s² und wird auch Schwerebeschleunigung oder Fallbeschleunigung genannt. Mit dieser Beschleunigung setzt sich ein frei fallender Körper in Bewegung.

Ein Schnurlot zeigt die Richtung des Schwerefeldes an

${\vec {g}}$ ist eine vektorielle Größe mit Betrag und Richtung. Die Richtung heißt Lotrichtung. Der Betrag wird auch Ortsfaktor genannt, um zu betonen, dass $g$ und damit auch das Gewicht eines Körpers vom Ort abhängt. In Deutschland beträgt die Fallbeschleunigung etwa 9,81 m/s² = 981 Gal. Die Variation über die Erdoberfläche beträgt wenige Gal.

Im engeren Sinne – insbesondere in den Geowissenschaften – ist das Schwerefeld eines Himmelskörpers zusammengesetzt aus dessen Gravitationsfeld („Erdanziehung“) und der Zentrifugalbeschleunigung in dem Bezugssystem, das mit dem Körper rotiert und ggf. mit ihm im Gravitationsfeld anderer Himmelskörper frei fällt.

In der Himmelsmechanik werden oft nicht rotierende Bezugssysteme benutzt. Das Schwerefeld eines oder mehrerer Himmelskörper beruht dann nur auf Gravitation.

Im weiteren Sinne spricht man vom Schwerefeld in beliebig beschleunigten Bezugssystemen. Im Schwerefeld einer Zentrifuge dominiert die Zentrifugalkraft. In frei fallenden Bezugssystemen (Bsp. Raumstation) herrscht Schwerelosigkeit.

Messung

Neben der direkten Messung der Beschleunigung eines frei fallenden Körpers kann man den Betrag der Fallbeschleunigung aus der Schwingungsdauer eines Pendels berechnen. Ein modernes Gravimeter ist eine spezielle Federwaage und erreicht eine Präzision von einem Mikrogal, ca. 10⁻⁹ g. Man könnte damit auf der Erde eine Höhenänderung von weniger als einem Zentimeter registrieren. Schwankungen des Luftdrucks beeinflussen den Auftrieb und verursachen damit Änderungen in der gleichen Größenordnung, Gebirge oder unterschiedliche Gesteinsdichten in der Erdkruste beeinflussen g sogar um bis zu 100 Milligal, etwas schwächer auch Gezeitenkräfte infolge der Inhomogenität äußerer Gravitationsfelder, insbesondere von Mond und Sonne.

Summe aus Gravitations- und Zentrifugalbeschleunigung

Die Fallbeschleunigung ist die Vektorsumme aus einem Gravitations- und einem Zentrifugalanteil:

{\vec {g}}={\vec {g}}_{\mathrm {Gravitation} }+{\vec {a}}_{\mathrm {Zentrifugal} }

Die Gravitationsbeschleunigung wird durch das Gravitationsfeld verursacht. Sofern man den Himmelskörper als kugelsymmetrisch betrachten kann, berechnet sich die Gravitationsbeschleunigung nach dem Gravitationsgesetz:

{\vec {g}}_{\mathrm {Gravitation} }=-{\frac {GM}{r^{2}}}\,{\vec {e}}_{r}

Hierbei ist

G

die Gravitationskonstante,

M

die Masse des Himmelskörpers,

r

der Abstand zwischen dem Schwerpunkt des Himmelskörpers und dem Probekörper und

{\vec {e}}_{r}

ein Einheitsvektor, der vom Schwerpunkt des Himmelskörpers auf den Probekörper gerichtet ist. Falls die Masseverteilung des Himmelskörpers nicht isotrop ist, wie das meist der Fall ist, ergeben sich daraus Schwereanomalien.

Die Zentrifugalbeschleunigung ${\vec {a}}_{\mathrm {Zentrifugal} }$ wirkt sich aus, weil man sich auf der Oberfläche des Himmelskörpers in einem mitrotierenden Bezugssystem befindet.

Gezeitenkräfte entstehen durch den Einfluss anderer Himmelskörper (z. B. durch den Mond oder die Sonne). Ob diese Kräfte als Teil des Schwerefeldes betrachtet werden, ist eine Frage der Definition. In diesem Artikel werden sie nicht zum Schwerefeld gezählt.

Für das Schwerefeld an einer Planetenoberfläche ergibt sich daraus: Die Gravitationsbeschleunigung ist von der Höhe abhängig, denn nach dem Gravitationsgesetz ist ${\vec {g}}_{\mathrm {Gravitation} }\sim {\tfrac {1}{r^{2}}}$ . Ebenfalls aus dieser Beziehung folgt, dass durch die Abplattung des Planeten der Abstand zum Planetenmittelpunkt an den Polen am kleinsten, die Gravitationswirkung deswegen am größten ist. Dazu kommt, dass an den Polen des Himmelskörpers die Zentrifugalbeschleunigung verschwindet, weil der Abstand von der Rotationsachse Null ist. Am schwächsten ist das Schwerefeld somit am Äquator: Dort ist die Zentrifugalbeschleunigung maximal und der Gravitationswirkung entgegen gerichtet und der Abstand zum Planetenmittelpunkt am größten.

Die Richtung der Fallbeschleunigung heißt Lotrichtung. Diese Lotrichtung weist ungefähr zum Gravizentrum des Himmelskörpers hin. Abweichungen entstehen (von Schwereanomalien abgesehen) dadurch, dass die Zentrifugalbeschleunigung bei mittleren Breiten in einem schiefen Winkel zur Gravitationsbeschleunigung steht. Linien, die der Lotrichtung folgen, heißen Lotlinien. Sie sind die Feldlinien des Schwerefeldes. Bewegt sich ein Körper im Schwerefeld, so weicht mit zunehmender Geschwindigkeit die Richtung der wirksamen Beschleunigung von der Lotrichtung ab. Dies kann als Wirkung der Corioliskraft gedeutet werden.

Schwerepotential

Da die Gewichtskraft eine konservative Kraft ist, ist die Fallbeschleunigung als zugehörige Feldstärke der negative Gradient eines Potentials U, ${\textstyle {\vec {g}}({\vec {r}})=-{\vec {\nabla }}U({\vec {r}})}$ . In der physikalischen Geodäsie wird aber nicht U, sondern W = −U verwendet und W trotz anderem Vorzeichen als Schwerepotential (bei der Erde auch Geopotential) bezeichnet. Mit dieser Konvention ist

{\vec {g}}({\vec {r}})=+{\vec {\nabla }}W({\vec {r}})

.

Das Schwerepotential setzt sich – ähnlich wie die Fallbeschleunigung selbst – aus einem Gravitations- und einem Zentrifugalanteil zusammen,

W({\vec {r}})=G\iiint \!{\frac {\rho ({\vec {r}}')}{|{\vec {r}}-{\vec {r}}'|}}\,\mathrm {d} ^{3}r'+{\frac {1}{2}}({\vec {\omega }}\times {\vec {r}})^{2}

.

Darin ist der erste Summand das Gravitationspotential in der allgemeinen Form für einen ausgedehnten Körper mit der Dichteverteilung $\rho ({\vec {r}}')$ . Für einen radialsymmetrischen Körper der Masse M vereinfacht es sich im Außenraum zu ${\textstyle G{\frac {M}{r}}}$ . Dieser Beitrag verschwindet im Unendlichen. Der zweite Summand, dessen Form voraussetzt, dass der Ursprung des Koordinatensystems auf der Rotationsachse liegt, ist das Potential der Zentrifugalbeschleunigung. Es kann mit dem Abstand ${\textstyle r_{\perp }}$ von der Rotationsachse auch als ${\textstyle {\frac {1}{2}}\omega ^{2}r_{\perp }^{2}}$ geschrieben werden. Dieser Beitrag verschwindet im Ursprung. Da beide Summanden nie negativ werden, nimmt W nur positive Werte an.[1]^:44,51[2]

Wasser in einem rotierenden Eimer. Sobald es ruhig mitrotiert, bildet seine Oberfläche eine Potentialfläche.

Flächen, auf denen das Schwerepotential konstant ist, heißen Potentialflächen oder Niveauflächen des Schwerefeldes. Sie werden von den Lotlinien rechtwinklig durchstoßen. Beim Übergang von einer Niveaufläche zu einer höheren muss Hubarbeit verrichtet werden, siehe auch Potential (Physik).

Geopotential

Das Schwerepotential W der Erde wird auch Geopotential genannt. Eine besonders wichtige Niveaufläche ist hier das Geoid, auf dem das Schwerepotential den Wert

W_{0}\approx W_{0,\mathrm {conv} }=62{.}636{.}856{,}0{\frac {\mathrm {m} ^{2}}{\mathrm {s} ^{2}}}

annimmt. Der hier genannte Wert ist als „konventionelles Geoidpotential“ bekannt. Er wird unter anderem in der Definition der Internationalen Atomzeit[3], vom Internationalen Dienst für Erdrotation und Referenzsysteme und von der IAU zur Definition der Terrestrischen Zeit verwendet.[4] Bei ihm handelt es sich um den besten im Jahr 1998 bekannten Messwert. Neuere Messungen ergeben aber einen um etwa 2,6 m²/s² kleineren Wert für W₀, was einem Höhenunterschied von 26 cm entspricht.[4] Potentialdifferenzen werden häufig auf W₀ bezogen,

C(P)=W_{0}-W_{P}=-\int _{P_{0}}^{P}{\vec {g}}\cdot \mathrm {d} {\vec {s}}

,

und dann geopotentielle Kote genannt[1]^:72 (Einheit geopotentieller Meter gpm). Wird die geopotentielle Kote durch die Normalschwere geteilt, so ergibt sich die dynamische Höhe. Für mittlere Breiten entspricht die dynamische Höhe ungefähr der metrischen Höhe über dem Meeresspiegel. Der Abstand zweier Äquipotentialflächen hängt von der lokalen Schwerebeschleunigung ab: Je größer diese ist, desto geringer ist der Abstand.

Allgemeinere Definition

Wählt man als Bezugssystem nicht die Oberfläche eines Planeten, sondern ein beliebiges beschleunigtes Bezugssystem, so kann die dort wirksame „Fall“-Beschleunigung ebenfalls als Schwerefeld verstanden werden. Auch die in diesem Bezugssystem herrschenden Kräfte setzen sich aus Gravitations- und Trägheitskräften zusammen.

Beispiele

In einem frei fallenden Bezugssystem sind die Gravitationskraft und die Trägheitskraft entgegengesetzt gleich. Ein Körper im frei fallenden Bezugssystem ist also schwerelos, d. h. kräftefrei. Also ist das frei fallende Bezugssystem ein Inertialsystem. Auch eine Raumstation, die sich in einer Umlaufbahn um die Erde befindet, befindet sich im „freien Fall“, da ihre Bewegung ausschließlich durch die Gravitation bestimmt wird. Die Schwerelosigkeit, d. h. das Verschwinden des Schwerefeldes an Bord dieser Raumstation ist also nicht die Folge einer Abwesenheit der Gravitation, sondern die Folge eines Gleichgewichts von Gravitationskraft und Trägheitskraft. (siehe Schwerelosigkeit).
Ein Planet bewegt sich auf einer Umlaufbahn der Sonne auf einer Kreis- oder Ellipsenbahn. Wählt man nun die Achse Sonne-Planet als Bezugssystem für die Bewegung eines dritten Körpers, z. B. einer Raumsonde, so wird das für diesen Körper wirksame Schwerefeld durch das Zusammenwirken der Gravitation beider Himmelskörper und des Zentrifugalfelds aufgrund der Rotation des Bezugssystems bestimmt. (siehe Lagrange-Punkte).

Erdschwerefeld

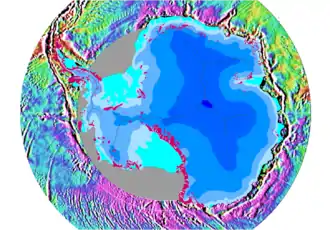
Schwerefeld der Erde im Südpolarmeer

Große Himmelskörper nehmen unter dem Einfluss ihres Schwerefeldes eine Form an, die einer der Niveauflächen entspricht. Im Schwerefeld der Erde wird jene Niveaufläche, die ungefähr der Höhe des Meeresspiegels folgt, als Geoid bezeichnet. Sie ist durch die Zentrifugalbeschleunigung leicht abgeplattet. Diese Abplattung und die Abnahme der Erdbeschleunigung (Fallbeschleunigung auf der Erde) mit der Höhe wird von Normalschwereformeln berücksichtigt. Zusätzlich gibt es Schwereanomalien, d. h. globale, regionale und lokale Unregelmäßigkeiten, da die Masse sowohl in der Erdkruste (Gebirge, Kontinentalplatten) als auch tiefer (in Erdmantel und -kern) nicht gleichmäßig verteilt ist. Die Satellitengeodäsie bestimmt das Geoid mit Hilfe der Beobachtung von Satellitenbahnen, siehe Gradiometrie. Die Schwereanomalien erreichen die Größenordnung 0,01 % und 0,01° in Betrag bzw. Richtung, siehe Lotabweichung, Schweregradient und Vertikalgradient. Bis zu 100 m liegen zwischen dem Geoid und dem mittleren Ellipsoid.

Erdschwerefeld an der Erdoberfläche

Der Wert der Erdbeschleunigung variiert wegen der Zentrifugalkraft, Erdabplattung und Höhenprofil regional um einige Promille um den ungefähren Wert 9,81 m/s². Die Erdbeschleunigung beträgt 9,832 m/s² an den Polen und 9,780 m/s² am Äquator. Die Anziehung am Pol ist somit um ca. 0,5 % größer als am Äquator. Wenn die Erdanziehungskraft auf einen Menschen am Äquator 800 N beträgt, so erhöht sie sich deshalb an den Erdpolen auf 804,24 N. Im Jahr 2013 wurde ermittelt, dass die Erdbeschleunigung mit 9,7639 m/s² auf dem Berg Nevado Huascarán in den Anden (höchster Berg Perus mit 6768 m) am geringsten ist.[5][6]

Normfallbeschleunigung

1901 wurde auf der dritten Generalkonferenz für Maß und Gewicht ein Standardwert, die Normfallbeschleunigung, auf g_n = 9,80665 m/s² festgelegt,[7][8] ein Wert, der sich schon in verschiedenen Landesgesetzen etabliert hatte und der Definition technischer Maßeinheiten dient (DIN 1305).[9] Grundlage waren (aus heutiger Sicht überholte) Messungen von G. Defforges am BIPM bei Paris, extrapoliert auf 45° (nördlicher, oder südlicher) Breite und Meereshöhe.[10]

Deutsches Hauptschwerenetz 1996

Kennzeichnungsplakette des Deutschen Schwerenetzes 1962

In Deutschland ist die ortsabhängige Erdbeschleunigung im Deutschen Hauptschwerenetz 1996 (DHSN 96) festgehalten, welches eine Fortsetzung des (westdeutschen) DHSN 82 ist. Es ist neben dem Deutschen Hauptdreiecksnetz für den Ort und dem Deutschen Haupthöhennetz für die Höhe die dritte Größe zur eindeutigen Festlegung eines geodätischen Bezugssystems. Das deutsche Schwerenetz stützt sich auf ca. 16.000 Messpunkte, die Schwerefestpunkte.

Historisch bedeutsam war der von Kühnen und Furtwänger vom Potsdamer Geodätischen Institut 1906 bestimmte Wert 9,81274 m/s² in Potsdam. Potsdam wurde 1906 der Fundamentalpunkt für die Bestimmung der lokalen Erdbeschleunigung mittels Differenzbestimmung, bis das International Gravity Standardization Net 1971 eingeführt wurde.[11][12]

Mit Einführung des Integrierten Raumbezugs 2016 wurde das DHSN 96 durch das DHSN 2016 abgelöst.

Erdschwerefeld im Erdinneren

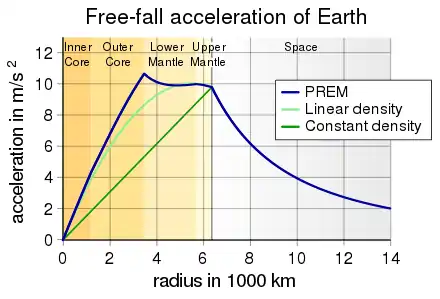
Gravitation im Erdinnern nach dem seismischen PREM-Erdmodell sowie Näherungen durch konstante und linear nach innen zunehmende Gesteinsdichte zum Vergleich.

Wäre die Erde eine nicht rotierende, homogene Kugel, so ergäbe sich ein linearer Anstieg der Schwerebeschleunigung von null am Erdmittelpunkt bis zu einem Maximum an der Erdoberfläche. Tatsächlich ist die Erde in Schichten sehr unterschiedlicher Dichte aufgebaut. Daher ist der Zusammenhang zwischen der Tiefe und der Erdbeschleunigung komplizierter. Im Erdkern wächst die Schwerebeschleunigung mit dem Abstand vom Erdmittelpunkt zunächst gleichmäßig an. An der Kern-Mantel-Grenze (in ca. 2900 km vom Erdmittelpunkt), nach deren Entdeckern Emil Wiechert und Beno Gutenberg auch Wiechert-Gutenberg-Diskontinuität genannt, erreicht sie ein Maximum von knapp 10,68 m/s². Dieser Effekt hat seine Ursache darin, dass der überwiegend metallische Erdkern mehr als doppelt so dicht wie der Erdmantel und die Erdkruste ist. Von dort bis zu ca. 4900 km nimmt sie zunächst wieder langsam bis auf 9,93 m/s² ab, steigt nochmals bei 5700 km auf 10,01 m/s² und sinkt dann monoton, bis sie an der Erdoberfläche etwa 9,82 m/s² erreicht.

Erdschwerefeld außerhalb der Erde

In der Nähe der Erdoberfläche nimmt g um etwa 3,1 µm/s² pro gestiegenem Meter ab. In der Meteorologie gibt man das Geopotential in der Atmosphäre als Äquipotentialflächen an. Für die Praxis hat man Hauptdruckflächen definiert (1000, 500, 200 hPa, und andere).

Außerhalb der Erde nimmt das Gravitationsfeld proportional zum Quadrat des Abstandes vom Erdmittelpunkt ab, während bei konstanter Position bzgl. Längen- und Breitengrad die Zentrifugalbeschleunigung proportional mit diesem Abstand zunimmt. Das Erdschwerefeld ist somit (wie das Schwerefeld jedes Körpers) prinzipiell unbegrenzt, wird aber mit wachsender Entfernung schnell schwächer. In niedrigen Satellitenhöhen von 300 bis 400 km nimmt die Erdbeschleunigung um 10 bis 15 % ab, in 5000 km um ca. 70 %. In einer Höhe von knapp 36.000 km heben sich beide Einflüsse exakt auf. Folglich bewegt sich ein Satellit auf einer solchen geostationären Umlaufbahn genau synchron mit der Erddrehung und verharrt auf demselben Längengrad.

Nur im Nahbereich eines schweren Himmelskörpers kann der Einfluss der anderen Himmelskörper in der Praxis vernachlässigt werden, da er dann sehr gering ist – der Einfluss des nahen Körpers ist dominierend.

Schwere- und Gravitationsbeschleunigung von Himmelskörpern

Sterne und andere Gas- bzw. Plasmakörper haben eine nicht trivial definierte Sternoberfläche, an der ihre Oberflächenbeschleunigung angegeben werden kann. Diese hängt nicht nur stark von ihrer Masse, sondern auch von ihrer Dichte ab. Ein Riesenstern hat einen sehr viel größeren Sternradius, wodurch seine Oberflächenbeschleunigung kleiner als die der Sonne ist.

Da die Oberflächenbeschleunigung von Himmelskörpern über viele Größenordnungen schwankt, wird sie in der Astrophysik häufig in logarithmischer Form (log g) angegeben. Dabei wird die Oberflächenbeschleunigung g in der Einheit cm/s² implizit durch die Bezugsgröße 1 cm/s² geteilt (wodurch sie einheitenlos wird) und davon der Logarithmus zur Basis 10 berechnet. Zum Beispiel hat die Sonne eine Oberflächenbeschleunigung g von ca. 27.400 cm/s². Hieraus ergibt sich für log g ein Wert von ca. 4,44.

Beispiele verschiedener Himmelskörper

Himmelskörper	log g[13]
Sonne (Gelber Zwerg)	4,44
Beteigeuze (Roter Riese)	ca. −0,6
Sirius B (Weißer Zwerg)	ca. 8
Gliese 229 B (Brauner Zwerg)	ca. 5

Ausgewählte Himmelskörper des Sonnensystems

Durch die Rotation des Himmelskörpers verringert sich seine Schwerebeschleunigung durch die Zentrifugalbeschleunigung. Die folgende Tabelle enthält die Gravitations-, die äquatoriale Zentrifugal- und die resultierende Schwerebeschleunigung der Sonne, der acht Planeten, Plutos und einiger Monde des Sonnensystems. Das negative Vorzeichen der Zentrifugalbeschleunigung soll verdeutlichen, dass diese der Gravitationsbeschleunigung entgegengerichtet ist.

	Himmels- körper	Beschleunigung in m/s²
	Himmels- körper	Gravitation[14][1]	Zentrifugal[15]	Schwere[14][1]
	Sonne	274,0	−0,0057	274,0
1	Merkur	003,70	−3,75·10⁻⁶	003,70
2	Venus	008,87	−0,541·10⁻⁶	008,87
3	Erde	009,80665	−0,0339	009,780
	Mond	001,622	−12,3·10⁻⁶	001,622
4	Mars	003,711	−0,0171	003,69
5	Jupiter	024,79	−2,21	023,12
	Io	001,81	−0,007	001,796
	Amalthea	000,02	−0,003	000,017
6	Saturn	010,44	−1,67	008,96
7	Uranus	008,87	−0,262	008,69
8	Neptun	011,15	−0,291	011,00
	Larissa	000,0355	−0,00186	000,0336
	Pluto	000,62	−154·10⁻⁶	000,62

Siehe auch

Einflusssphäre (Astronomie)

Literatur

Douglas Roy Tate: Gravity measurements and the Standards Laboratory. In: U.S. National Bureau of Standards. Technical note, 491. Superintendent of Documents, United States Government Printing Office, Washington 1969. hdl:2027/mdp.39015077289141 HathiTrust Digital Library.
Christoph Reigber, Peter Schwintzer: Das Schwerefeld der Erde. In: Physik in unserer Zeit. Band 34, Nr. 5, September 2003, S. 206–212, doi:10.1002/piuz.200301023.

Weblinks

Literatur von und über Schwerefeld im Katalog der Deutschen Nationalbibliothek
Berechnen des Wertes der Schwerebeschleunigung für beliebige Orte (Gravity Information System der PTB)
GGMplus – 200m-resolution maps of Earth’s gravity field Gallery. Western Australian Center for Geodesy, Curtin University

Einzelnachweise

Wolfgang Torge: Geodäsie. 2. Auflage. de Gruyter, 2003, ISBN 3-11-017545-2 (eingeschränkte Vorschau in der Google-Buchsuche).
Martin Vermeer: Physical geodesy. School of Engineering, Aalto University, 2020, ISBN 978-952-60-8940-9, S. 10, 88 (englisch, Volltext [PDF]): “In physical geodesy — unlike in physics — the potential is reckoned to be always positive …”
Resolution 2 of the 26th CGPM. On the definition of time scales. Bureau International des Poids et Mesures, 2018, abgerufen am 16. April 2021 (englisch).
A conventional value for the geoid reference potential W₀. (PDF) In: Unified Analysis Workshop 2017. Deutsches Geodätisches Forschungsinstitut, S. 5–7, abgerufen am 23. Februar 2020 (englisch).
Luh: Erdbeschleunigung schwankt stärker als gedacht dradio – Forschung Aktuell, 20. August 2013.
Gravity Variations Over Earth Much Bigger Than Previously Thought in Science Daily vom 4. September 2013.
Comptes rendus de la 3^e CGPM (1901), Seite 70, dort noch in cm/s².
Resolution 2 of the 3rd CGPM. Declaration on the unit of mass and on the definition of weight; conventional value of g_n. Bureau International des Poids et Mesures, 1901, abgerufen am 16. April 2021 (englisch).
Norm DIN 1305 Masse, Wägewert, Kraft, Gewichtskraft, Gewicht, Last; Begriffe (beuth.de).
Tate, 1969.
Landesamt für innere Verwaltung (LAiV) Mecklenburg-Vorpommern: Raumbezug - Lage-, Höhen- und Schwerefestpunktfelder (Memento vom 14. Januar 2014 im Internet Archive)
Tate, 1969.
Stanimir Metchev: Fundamental (Sub)stellar Parameters II. Surface Gravity (Vorlesungsfolien, 2009, englisch)
David R. Williams: Planetary Fact Sheet - Metric. NASA, 29. November 2007, abgerufen am 4. August 2008 (englisch, inkl. Unterseiten).
Deutschschweizerische Mathematikkommission [DMK] und Deutschschweizerische Physikkommission [DPK] (Hrsg.): Formeln und Tafeln. 11. Auflage. Orell Füssli Verlag, Zürich 2006, ISBN 978-3-280-02162-0, S. 188.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Toge03-1] Wolfgang Torge: Geodäsie. 2. Auflage. de Gruyter, 2003, ISBN 3-11-017545-2 (eingeschränkte Vorschau in der Google-Buchsuche).

[Vermeer20-2] Martin Vermeer: Physical geodesy. School of Engineering, Aalto University, 2020, ISBN 978-952-60-8940-9, S. 10, 88 (englisch, Volltext [PDF]): “In physical geodesy — unlike in physics — the potential is reckoned to be always positive …”

[CGPM-26-2-3] Resolution 2 of the 26th CGPM. On the definition of time scales. Bureau International des Poids et Mesures, 2018, abgerufen am 16. April 2021 (englisch).

[geopot17-4] A conventional value for the geoid reference potential W₀. (PDF) In: Unified Analysis Workshop 2017. Deutsches Geodätisches Forschungsinstitut, S. 5–7, abgerufen am 23. Februar 2020 (englisch).

[5] Luh: Erdbeschleunigung schwankt stärker als gedacht dradio – Forschung Aktuell, 20. August 2013.

[6] Gravity Variations Over Earth Much Bigger Than Previously Thought in Science Daily vom 4. September 2013.

[7] Comptes rendus de la 3^e CGPM (1901), Seite 70, dort noch in cm/s².

[CGPM-3-2-8] Resolution 2 of the 3rd CGPM. Declaration on the unit of mass and on the definition of weight; conventional value of g_n. Bureau International des Poids et Mesures, 1901, abgerufen am 16. April 2021 (englisch).

[9] Norm DIN 1305 Masse, Wägewert, Kraft, Gewichtskraft, Gewicht, Last; Begriffe (beuth.de).

[10] Tate, 1969.

[11] Landesamt für innere Verwaltung (LAiV) Mecklenburg-Vorpommern: Raumbezug - Lage-, Höhen- und Schwerefestpunktfelder (Memento vom 14. Januar 2014 im Internet Archive)

[12] Tate, 1969.

[13] Stanimir Metchev: Fundamental (Sub)stellar Parameters II. Surface Gravity (Vorlesungsfolien, 2009, englisch)

[nasa-14] David R. Williams: Planetary Fact Sheet - Metric. NASA, 29. November 2007, abgerufen am 4. August 2008 (englisch, inkl. Unterseiten).

[15] Deutschschweizerische Mathematikkommission [DMK] und Deutschschweizerische Physikkommission [DPK] (Hrsg.): Formeln und Tafeln. 11. Auflage. Orell Füssli Verlag, Zürich 2006, ISBN 978-3-280-02162-0, S. 188.