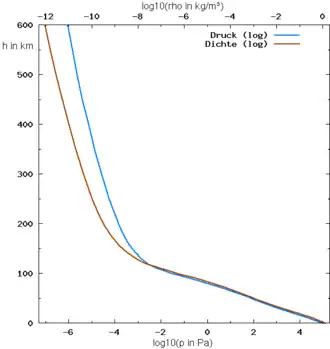
Barometrische Höhenformel

Die barometrische Höhenformel beschreibt die vertikale Verteilung der (Gas-)Teilchen in der Atmosphäre der Erde, also die Abhängigkeit des Luftdruckes von der Höhe. Man spricht daher auch von einem vertikalen Druck-Gradienten, der jedoch aufgrund der hohen Wetterdynamik innerhalb der unteren Atmosphäre nur mit Näherungen auf mathematischem Wege beschrieben werden kann.

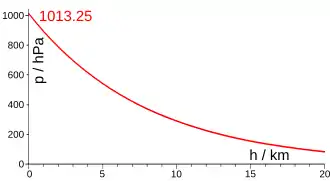
Durchschnittlicher Druck und Dichte in Abhängigkeit von der Höhe. Logarithmische Darstellung für große Höhen

Lineare Darstellung für geringe Höhen

In der einfachsten Form kann grob angenommen werden, dass der Luftdruck in der Nähe des Meeresspiegels um ein Hektopascal (entsprechend 1 ‰ des mittleren Luftdrucks) je acht Meter Höhenzunahme abnimmt. 1 hPa = 100 N/m², 8 m³ Luft haben eine Gewichtskraft 100 N.

Etwas besser ist die Näherung, dass der Druck mit zunehmender Höhe exponentiell abnimmt. Dieser Zusammenhang war 1686 erstmals von Edmond Halley erkannt worden.[1]

Hydrostatische Grundgleichung

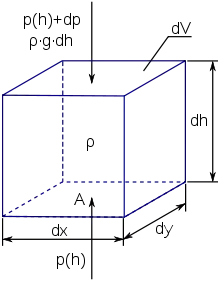
Volumenelement mit den maßgebenden Einflüssen

Die Änderung von Druck und Dichte der Atmosphäre mit der Höhe wird durch die hydrostatische Grundgleichung beschrieben. Zur Herleitung betrachte man ein quaderförmiges Volumenelement mit der Grundfläche $A\,$ und der infinitesimal kleinen Höhe $\mathrm {d} h\,$ , welches Luft der Dichte $\rho \,$ enthält. Von unten wirkt auf die Grundfläche nur die vom Atmosphärendruck $p\,$ ausgeübte Kraft $p\cdot A$ . Die von oben auf die Grundfläche wirkende Kraft setzt sich zusammen aus der Gewichtskraft $\mathrm {d} m\cdot g=\rho \,\mathrm {d} V\cdot g=\rho g\,\mathrm {d} h\cdot A$ der im Volumen $\mathrm {d} V=A\cdot \mathrm {d} h$ enthaltenen Luftmasse $\mathrm {d} m\,$ und der vom Atmosphärendruck auf die Oberseite ausgeübten Kraft. Der Atmosphärendruck ist in dieser Höhe um den Betrag $\mathrm {d} p\,$ verschieden von dem auf die Unterseite wirkenden Druck; die durch ihn ausgeübte Kraft ist daher $(p+\mathrm {d} p)\cdot A$ .

Im hydrostatischen Gleichgewicht sind alle Luftströmungen zur Ruhe gekommen. Damit das Gleichgewicht erhalten und das betrachtete Volumenelement auch weiterhin in Ruhe bleibt, muss die Summe aller darauf wirkenden Kräfte null sein:

p\cdot A-\rho g\,\mathrm {d} h\cdot A-(p+\mathrm {d} p)\cdot A=0

Kürzen und Umstellen liefert

{\frac {\mathrm {d} p}{\mathrm {d} h}}=-\rho g

Nach dem idealen Gasgesetz lässt sich die Dichte $\rho \,$ ausdrücken als $\rho ={\tfrac {pM}{RT}}$ ,

so dass sich schließlich ergibt:

{\frac {\mathrm {d} p}{\mathrm {d} h}}=-{\frac {pMg}{RT}}

Dabei ist

$M$ die mittlere molare Masse der Atmosphärengase (0,02896 kg mol⁻¹),
$g$ die Schwerebeschleunigung (9,807 m s⁻²),
$R$ die universelle Gaskonstante (8,314 J K⁻¹ mol⁻¹) und
$T$ die absolute Temperatur.

Die hydrostatische Grundgleichung gibt an, um welchen Betrag $\mathrm {d} p$ sich der Atmosphärendruck ändert, wenn sich die Höhe um einen kleinen Betrag $\mathrm {d} h$ ändert. Wie das negative Vorzeichen zeigt, ist $\mathrm {d} p$ negativ, wenn $\mathrm {d} h$ positiv ist; der Druck wird mit zunehmender Höhe also geringer. So nimmt beispielsweise bei mittlerem Luftdruck auf Meereshöhe ( $p$ = 1013 hPa) bei einer Temperatur von 288 K (= 15 °C) der Druck auf einem Meter Höhenunterschied um 0,12 hPa beziehungsweise auf 8,3 Metern Höhenunterschied um 1 hPa ab. Der Höhenunterschied, der einem Druckunterschied von 1 hPa entspricht, ist die barometrische Höhenstufe. In größeren Höhen (kleineres $p$ ) und bei höheren Temperaturen $T$ verändert sich der Luftdruck langsamer, die barometrische Höhenstufe nimmt zu.

In der Regel werden explizite Werte für Druck und Dichte auf vorgegebenen Höhen benötigt. Daraus lassen sich bei Bedarf auch die Druckunterschiede für größere Höhenunterschiede ablesen. Die gesuchte Lösung der Grundgleichung erhält man durch Trennung der Variablen

{\frac {\mathrm {d} p}{p}}=-{\frac {Mg}{RT}}\,\mathrm {d} h

und anschließende Integration zwischen den gesuchten Höhen beziehungsweise den zugehörigen Drücken:

\int _{p(h_{0})}^{p(h_{1})}{\frac {\mathrm {d} p}{p}}=-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h

.

Integration der linken Seite ergibt $\ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)$ . Zur Integration der rechten Seite muss die Höhenabhängigkeit von $g$ und $T$ bekannt sein. Die Schwerebeschleunigung $g$ kann für nicht zu große Höhen als konstant angesehen werden. Die Temperatur $T$ variiert in komplizierter und kaum vorhersagbarer Weise mit der Höhe. Es müssen daher vereinfachende Annahmen über den Temperaturverlauf $T(h)$ getroffen werden.

Isotherme Atmosphäre

Die in einführender Literatur und im Schulunterricht meist zitierte klassische barometrische Höhenformel gilt für den Spezialfall, dass die Temperatur $T$ in jeder Höhe gleich, die Atmosphäre also isotherm ist.

Herleitung aus der hydrostatischen Grundgleichung

Die Integration der hydrostatischen Grundgleichung liefert bei konstantem $T$ :

{\begin{aligned}&&\int _{p(h_{0})}^{p(h_{1})}{\frac {\mathrm {d} p}{p}}&=-{\frac {Mg}{RT}}\,\int _{h_{0}}^{h_{1}}\mathrm {d} h\\\iff &&\ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)&=-{\frac {Mg}{RT}}(h_{1}-h_{0})=-{\frac {Mg}{RT}}\Delta h\\\iff &&{\frac {p(h_{1})}{p(h_{0})}}&=\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}\\\iff &&p(h_{1})&=p(h_{0})\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}\end{aligned}}

Durch Einführung der Skalenhöhe $h_{s}={\tfrac {RT}{Mg}}$ vereinfacht sich die Höhenformel zu

p(h_{1})=p(h_{0})\mathrm {e} ^{-{\frac {\Delta h}{h_{s}}}}

Mit jeder Höhenzunahme um $h_{s}$ nimmt der Luftdruck um den Faktor $\mathrm {e} \approx 2{,}7$ ab. Die Skalenhöhe ist daher ein natürliches Maß für die Höhe der Atmosphäre und den Druckverlauf in ihr. Sie beträgt in der hier angenommenen Modellatmosphäre bei einer Temperatur von 15 °C etwa 8,4 km.

Für die Dichte gilt entsprechend:

\rho (h_{1})=\rho (h_{0})\mathrm {e} ^{-{\frac {\Delta h}{h_{s}}}}

Für einen bergab wandernden Beobachter nimmt der Luftdruck ständig zu, da eine immer schwerere Luftsäule auf ihm lastet. Die Zunahme verläuft exponentiell, da die Luft kompressibel ist: für jeden Meter Höhenunterschied nimmt die Gewichtskraft der auf einer Messfläche lastenden Luftsäule um das Gewicht des auf dieser Strecke hinzukommenden Säulenvolumens zu. Dieses Gewicht hängt aber von der Dichte der Luft und diese wiederum vom Luftdruck ab. Der Luftdruck wächst also umso schneller, je höher der Luftdruck bereits ist (je weiter der Beobachter also herabgestiegen ist). Ändert sich eine Größe stets um einen Betrag, der der Größe selbst proportional ist, so geschieht die Änderung exponentiell.

Obwohl der Druck nicht konstant ist, befindet sich die Luftsäule im mechanischen Gleichgewicht: Der negative Druckgradient ist gleich der Schwerkraft pro Volumenelement $-\partial _{z}p(z)=g\rho (z)$

Herleitung aus der statistischen Mechanik

In einem Teilchensystem, das sich bei der Temperatur $T$ im thermischen Gleichgewicht befindet (das also insbesondere überall dieselbe Temperatur aufweist) und dessen Teilchen die kontinuierlich oder diskret verteilten Energieniveaus $E_{j}$ einnehmen können, ist die Wahrscheinlichkeit, dass sich ein Teilchen gerade auf dem Energieniveau $E_{j}$ befindet, gegeben durch die Boltzmann-Verteilung

P_{j}={\frac {\mathrm {e} ^{-{\frac {E_{j}}{k_{\mathrm {B} }T}}}}{Z}}

.

Dabei ist $k_{\mathrm {B} }$ die Boltzmann-Konstante und $Z$ ein Normierungsfaktor (die so genannte Zustandssumme), der sicherstellt, dass die Summe über alle Wahrscheinlichkeiten gleich 1 ist. Besteht das System aus $N$ Teilchen, so ist die Anzahl der Teilchen auf dem Energieniveau $E_{j}$ im Mittel $n_{j}=NP_{j}$ .

Ein Gasteilchen der Masse $m$ hat im Schwerefeld der Erde die potentielle Energie $E_{\mathrm {pot} }=mgh$ und wegen seiner Temperatur im Mittel die thermische Energie $E_{\mathrm {th} }$ , insgesamt also die Energie $E(h)=mgh+E_{\mathrm {th} }$ . Betrachtet man zwei gleich große Volumenelemente auf den Höhen $h_{0}$ beziehungsweise $h_{1}$ , so haben die Teilchen auf der Höhe $h_{1}$ eine um den Betrag $mg\Delta h$ höhere Energie. Die Wahrscheinlichkeit, ein Teilchen im höheren Volumenelement anzutreffen, verhält sich daher zur Wahrscheinlichkeit, es im tieferen Volumenelement anzutreffen wie

{\frac {P(h_{1})}{P(h_{0})}}={\frac {\mathrm {e} ^{-{\frac {E(h_{1})}{k_{\mathrm {B} }T}}}}{\mathrm {e} ^{-{\frac {E(h_{0})}{k_{\mathrm {B} }T}}}}}=\mathrm {e} ^{-{\frac {\Delta E}{k_{\mathrm {B} }T}}}=\mathrm {e} ^{-{\frac {\Delta E_{\mathrm {pot} }}{k_{\mathrm {B} }T}}}

.

Für eine hinreichend große Anzahl $N$ von Teilchen verhalten sich die Teilchendichten $n(h)$ wie die Aufenthaltswahrscheinlichkeiten

{\frac {n(h_{1})}{n(h_{0})}}={\frac {NP(h_{1})}{NP(h_{0})}}=\mathrm {e} ^{-{\frac {\Delta E_{\mathrm {pot} }}{k_{\mathrm {B} }T}}}

,

und wegen des idealen Gasgesetzes folgt für den Druck $p(h)=n(h)\,k_{\mathrm {B} }T$ dasselbe Verhältnis

{\frac {p(h_{1})}{p(h_{0})}}=\mathrm {e} ^{-{\frac {\Delta E_{\mathrm {pot} }}{k_{\mathrm {B} }T}}}=\mathrm {e} ^{-{\frac {mg\Delta h}{k_{\mathrm {B} }T}}}=\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}

,

wobei man die molare Masse $M$ und die Gaskonstante $R$ erhält, indem man die Teilchenmasse $m$ beziehungsweise die Boltzmann-Konstante $k_{\mathrm {B} }$ mit der Avogadro-Konstante multipliziert.

Allerdings wird hier bei der Energie-Betrachtung der Gleichverteilungssatz vorausgesetzt. Diese Voraussetzung ist aber allgemein nur in dichter Atmosphäre erfüllt, weil nur dort durch Stöße zwischen den Gasmolekülen die Energien zwischen den verschiedenen Freiheitsgraden ausgetauscht werden. Der Grund dafür, dass der Gleichverteilungssatz generell nicht für die Höhenenergie gilt, ist, dass der Gleichverteilungssatz direkt nur auf Potentiale angewendet werden kann, die quadratisch in die Hamilton-Funktion eingehen. Weil die Höhenenergie nur linear in die Hamilton-Funktion eingeht, kann man den Gleichverteilungssatz in sehr dünnen Gasen nicht einfach voraussetzen.

Atmosphäre mit linearem Temperaturverlauf

Der streng lineare Temperaturverlauf besteht nur in der idealisierten Vorstellung einer ruhenden Atmosphäre ohne Konvektion ohne Ausgleich des Temperaturgefälles durch Wärmeleitung. Um das besser verwendbar zu machen, wurde die potentielle Temperatur eingeführt. Obwohl der adiabatische Gradient ein Temperaturgefälle ist, ist die potentielle Temperatur konstant, d. h. ein Gleichgewicht. Mit der potentiellen Energie eines Teilchens im Gravitationsfeld ( $E=mgh$ ) hat das nichts zu tun. Besonders deutlich wird das mit der Zahl der Freiheitsgrade. Teilchen gleicher Masse, aber unterschiedlicher Zahl an Freiheitsgraden haben unterschiedliche Temperaturgradienten.

Da für die Aufrechterhaltung des linearen Temperaturverlaufs die Wärmeleitung keine Rolle spielen darf, darf in der Realität der permanente „Wärmetransport“ (Wärmeleitung) durch schnelle Zirkulation nur einen geringen Einfluss haben. Weil Konvektionslosigkeit und Zirkulation nicht gleichzeitig vorkommen können, wird der lineare Verlauf immer leicht modifiziert durch Wärmetransport aller Art, der bekannteste ist die Kondensation von Wasserdampf, die zu einem geringeren Temperaturabfall führt („feucht-adiabatisch“, eine etwas irreführende Bezeichnung).

Temperaturverteilung (Adiabatische Atmosphäre)

Aus der Gleichung für die Druckänderung

{\frac {\mathrm {d} p}{p}}=-{\frac {Mg}{RT}}\,\mathrm {d} h

und der mit Hilfe logarithmischer Ableitungen geschriebenen Gleichung für die adiabatische Zustandsänderung

{\frac {\mathrm {d} p}{p}}={\frac {\kappa }{\kappa -1}}\ {\frac {\mathrm {d} T}{T}}

folgt sofort die lineare Temperaturabnahme gemäß

\mathrm {d} T=-{\frac {Mg}{R\ \kappa /(\kappa -1)}}\ \mathrm {d} h

Mit der mittleren molaren Masse des Atmosphärengases M = 0,02896 kg mol⁻¹, der Schwerebeschleunigung g = 9,807 m s⁻², der universellen Gaskonstante R = 8,314 J K⁻¹ mol⁻¹ und dem Adiabatenexponenten von (trockener) Luft $\kappa$ = 1,402 erhält man den Temperaturgradienten

{\frac {\mathrm {d} T}{\mathrm {d} h}}=-\,{\frac {0{,}979\,\mathrm {K} }{100\,\mathrm {m} }}

Dies ist näherungsweise der unten angegebene Temperaturgradient. Jener wird allerdings im Wesentlichen durch die feuchtadiabatische Expansion bestimmt: der feuchtadiabatische Adiabatenexponent ist kleiner als der trockenadiabatische Adiabatenexponent. Bei einer reinen Wasserdampfatmosphäre wäre der Temperaturgradient

\left.{\frac {\mathrm {d} T}{\mathrm {d} h}}\right|_{\mathrm {H_{2}O} }=-{\frac {0{,}562\,\mathrm {K} }{100\,\mathrm {m} }}

Weitere Grenzen des adiabatischen Ansatzes: Wird die Luft sehr kalt, ändert sich auch bei trockener Luft der Adiabatenexponent. Bei sehr großen Höhen (geringe Dichte) wird auch die mittlere freie Weglänge sehr groß, so dass die Gasgleichungen kaum noch gelten. Dazu kommt noch, dass durch den Treibhauseffekt auch der adiabatische Ansatz (kein Energieaustausch mit der Umgebung) verletzt wird.

Dichte- und Druckverteilung

Im Allgemeinen ist die Temperatur nicht konstant, sondern variiert mit der Höhe. Der einfachste Ansatz zur Berücksichtigung einer solchen Veränderlichkeit geht von einer linearen Abnahme mit der Höhe aus. Aus der adiabatischen Beziehung folgt wie oben beschrieben ein konstanter Temperaturgradient

a=-{\frac {\mathrm {d} T}{\mathrm {d} h}}={\frac {\kappa -1}{\kappa }}{\frac {Mg}{R}}

sodass für die Temperatur $T(h)$ gilt:

T(h)=T(h_{0})-a\cdot (h-h_{0})\qquad \Rightarrow \qquad T(h)=T(h_{0})\cdot \left(1-{\frac {a(h-h_{0})}{T(h_{0})}}\right)=T(h_{0})\cdot \left(1-{\frac {a\Delta h}{T(h_{0})}}\right)

,

wobei $a$ der (positiv zu nehmende) Betrag des vertikalen atmosphärischen Temperaturgradienten ist, der angibt, um wie viele Kelvin die Lufttemperatur pro Meter Höhenunterschied abnimmt. Das Integral über die rechte Seite der Grundgleichung lautet damit

-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h=-\int _{h_{0}}^{h_{1}}{\frac {Mg}{R\,(T(h_{0})-a\cdot (h-h_{0}))}}\,\mathrm {d} h=-{\frac {Mg}{R}}\int _{h_{0}}^{h_{1}}{\frac {1}{(T(h_{0})+ah_{0})-ah}}\,\mathrm {d} h

.

Wegen

\int {\frac {1}{b-ax}}\,\mathrm {d} x=-{\frac {1}{a}}\,\ln(b-ax)

ist die Lösung des Integrals

-{\frac {1}{a}}\ln(\,(T(h_{0})+ah_{0})-ah)\vert _{h_{0}}^{h_{1}}=-{\frac {1}{a}}\ln \left({\frac {T(h_{0})-a(h_{1}-h_{0})}{T(h_{0})}}\right)

,

so dass insgesamt aus dem Integral über die Grundgleichung

\ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)=+{\frac {Mg}{R}}\,{\frac {1}{a}}\ln \left({\frac {T(h_{0})-a(h_{1}-h_{0})}{T(h_{0})}}\right)=+{\frac {Mg}{R}}\,{\frac {1}{a}}\ln \left(1-{\frac {a\Delta h}{T(h_{0})}}\right)

die barometrische Höhenformel für linearen Temperaturverlauf folgt:

p(h_{1})=p(h_{0})\mathrm {e} ^{+{\frac {Mg}{R}}{\frac {1}{a}}\ln \left(1-{\frac {a\Delta h}{T(h_{0})}}\right)}

,

oder wegen $\mathrm {e} ^{y\cdot \ln(x)}=x^{y}$

p(h_{1})=p(h_{0})\left(1-{\frac {a\Delta h}{T(h_{0})}}\right)^{\frac {Mg}{Ra}}=p(h_{0})\left(1-{\frac {\kappa -1}{\kappa }}{\frac {Mg\Delta h}{RT(h_{0})}}\right)^{\frac {\kappa }{\kappa -1}}

Für die Dichte gilt entsprechend

\rho (h_{1})=\rho (h_{0})\left(1-{\frac {a\Delta h}{T(h_{0})}}\right)^{\frac {Mg}{Ra\kappa }}=\rho (h_{0})\left(1-{\frac {\kappa -1}{\kappa }}{\frac {Mg\Delta h}{RT(h_{0})}}\right)^{\frac {1}{\kappa -1}}

Der Exponent ist hier durch $\kappa$ geteilt, da der Dichte/Druck-Zusammenhang aus der adiabatischen Beziehung der beiden Größen resultiert.

Diese erweiterte barometrische Höhenformel bildet die Grundlage für die barometrische Höhenfunktion der Standardatmosphäre in der Luftfahrt. Dabei wird zunächst die Atmosphäre in Teilschichten mit jeweils linear interpoliertem Temperaturverlauf unterteilt. Dann werden, mit der untersten Schicht beginnend, Temperatur und Druck an der Obergrenze der jeweiligen Teilschicht berechnet und für die Untergrenze der darüber liegenden Schicht eingesetzt. Auf diese Weise entsteht induktiv das Modell für die gesamte Atmosphäre.

Typische Temperaturgradienten

Wie Messungen der Temperaturprofile in der Atmosphäre zeigen, ist die Annahme einer linearen Temperaturabnahme im Mittel eine gute Näherung, wenn auch im Einzelfall deutliche Abweichungen auftreten können, zum Beispiel bei Inversionswetterlagen. Die Hauptursache für die Temperaturabnahme mit der Höhe ist die Erwärmung der unteren Luftschichten durch die von der Sonne aufgeheizte Erdoberfläche, während die oberen Luftschichten Wärme in den Weltraum abstrahlen. Dazu kommen trockenadiabatische oder feuchtadiabatische Temperaturänderungen einzelner aufsteigender oder absinkender Luftpakete und zusätzliche Modifikationen durch Vermischungsvorgänge zwischen Luftmassen unterschiedlicher Herkunft.

In Warmluftmassen und bei Aufgleitvorgängen nimmt der Temperaturgradient Werte um 0,3 bis 0,5 K pro 100 m an, in einbrechender Kaltluft meist um 0,6 bis 0,8 K pro 100 m, im Mittel über alle Wetterlagen 0,65 K pro 100 m. In Tallagen können häufige Bodeninversionen den mittleren Temperaturgradienten auf 0,5 K pro 100 m senken, in den Wintermonaten sogar auf 0,4 K pro 100 m.[2]

Die beschriebenen Verhältnisse sind auf die Troposphäre beschränkt. In der Stratosphäre nimmt die Temperatur deutlich langsamer ab, meist nimmt sie sogar wieder zu, vor allem wegen der Absorption von UV-Strahlung in der Ozonschicht.

Für einen Temperaturgradienten von 0,65 K pro 100 m nimmt der Exponent $\mathrm {\tfrac {Mg}{Ra}}$ den Wert 5,255 an:

p(h_{1})=p(h_{0})\left(1-{\frac {0{,}0065\cdot \Delta h}{T(h_{0})}}\right)^{5{,}255}

Wird der Exponent durch den Isentropenkoeffizienten $\kappa$ ausgedrückt, so wird:

5{,}255={\frac {\kappa }{\kappa -1}}\quad \Rightarrow \quad \kappa =1{,}235

Das bedeutet 8,5 Freiheitsgrade.

Aus dem Temperaturgradienten ergibt sich auch die mittlere Wärmekapazität der Luft über alle Wetterlagen:

{\frac {\mathrm {d} T}{\mathrm {d} h}}={\frac {0{,}65\,\mathrm {K} }{100\,\mathrm {m} }}={\frac {g}{c_{p}}}={\frac {9{,}81\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}}{c_{p}}}\quad \Rightarrow \quad c_{p}=1509\,{\frac {\mathrm {m} ^{2}}{\mathrm {K} ~\mathrm {s} ^{2}}}=1509\,{\frac {\mathrm {Ws} }{\mathrm {kg~K} }}

Dieser Wert liegt zwischen dem Wert von trockener Luft (1005 Ws/(kg K)) und Wasserdampf (2034 Ws/(kg K)).

Die nachfolgende Tabelle zeigt den Zusammenhang zwischen Höhe und Druck (im Mittel):

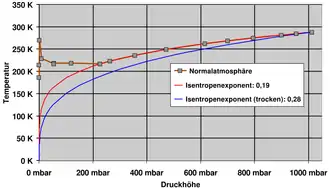
Temperaturverlauf der Atmosphäre als Funktion der Druckhöhe (Erdoberfläche = 1,013 bar) – die Tropopause wird am besten mit einem Isentropenexponenten von 0,19 angenähert.

Höhe in m	Druck in hPa
0	1013,25
500	954,61
1000	898,76
1500	845,58
2000	794,98
2500	746,86
3000	701,12
3500	657,68
4000	616,45
4500	577,33
5000	540,25
6000	471,87
7000	410,66
8000	356,06
9000	307,48
10000	264,42
11000	226,37

In dieser Form bietet sich die Höhenformel für den häufigen Fall an, dass Temperatur und Luftdruck auf einer der beiden Höhen bekannt sind, nicht aber der zurzeit bestehende Temperaturgradient.

Die Höhenstufen

Die barometrische Höhenstufe ist die vertikale Strecke, die zurückgelegt werden muss, um 1 hPa Luftdruckänderung zu erzielen. In Bodennähe beträgt die barometrische Höhenstufe etwa 8 Meter, in 5,5 Kilometern Höhe 16 Meter und in 11 Kilometern Höhe 32 Meter.

Mit der Höhenformel ergibt sich folgende Tabelle für die Höhen- und Temperaturabhängigkeit der barometrischen Höhenstufe:

Barometrische Höhenstufe in m/hPa
h	−15 °C	0 °C	15 °C	30 °C
0 m	7,5	7,9	8,3	8,8
500 m	7,9	8,3	8,7	9,2
1000 m	8,3	8,7	9,2	9,6
2000 m	9,3	9,7	10,1	10,6
3000 m	10,4	10,8	11,2	11,6

Als Faustformel für mittlere Höhen und Temperaturen gilt „1 hPa/30 ft“. Diesen Rundungswert nutzen Luftfahrer häufig für überschlägige Berechnungen.

Internationale Höhenformel

Setzt man die Referenzhöhe $h_{0}$ auf Meereshöhe und nimmt für die dortige Atmosphäre einen mittleren Zustand an, wie er durch die Internationale Standardatmosphäre beschrieben wird (Temperatur 15 °C = 288,15 K, Luftdruck 1013,25 hPa, Temperaturgradient 0,65 K pro 100 m), so erhält man die Internationale Höhenformel für die Troposphäre (gültig bis 11 km Höhe):

p(h)=1013{,}25\cdot \left(1-{\frac {0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}\cdot h}{288{,}15\ \mathrm {K} }}\right)^{5{,}255}\mathrm {hPa}

{\color {White}p(h)}=p_{0}\cdot \left(1-{\frac {0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}\cdot h}{T_{0}\ }}\right)^{5{,}255}

Diese Formel erlaubt die Berechnung des Luftdrucks (in Gestalt des sog. Normaldrucks) auf einer gegebenen Höhe, ohne dass Temperatur und Temperaturgradient bekannt sind. Die Genauigkeit im konkreten Anwendungsfall ist allerdings begrenzt, da der Berechnung statt des aktuellen Atmosphärenzustands lediglich eine mittlere Atmosphäre zugrunde gelegt wird.

Internationale Höhenformel im Rahmen der Internationalen Standardatmosphäre nach der Höhe aufgelöst, zur Umrechnung des Luftdrucks p(h) (Normaldruck) in die damit korrespondierende Höhe in Metern (m):

h={\frac {288{,}15\ \mathrm {K} }{0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}}}\cdot \left(1-\left({\frac {p(h)}{1013{,}25\,\mathrm {hPa} }}\right)^{\frac {1}{5{,}255}}\right)

Allgemeiner Fall

Die Lösung der hydrostatischen Grundgleichung lautet allgemein

\ln \left({\frac {p(h_{1})}{p(h_{0})}}\right)=-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h

,

beziehungsweise

p(h_{1})=p(h_{0})\,\mathrm {e} ^{-\int _{h_{0}}^{h_{1}}{\frac {Mg}{RT}}\,\mathrm {d} h}

mit noch zu lösendem Integral.

Virtuelle Temperatur

Die Gaskonstante $R$ ist eine Naturkonstante und kann vor das Integral gezogen werden. Die mittlere molare Masse der Atmosphärengase $M$ ist, sofern vom stark variablen Wasserdampfgehalt abgesehen wird, innerhalb der Troposphäre ebenfalls praktisch konstant und kann auch vor das Integral gezogen werden. Die unterschiedlichen Skalenhöhen der verschieden schweren Atmosphärengase würden in einer ruhenden Atmosphäre zwar zu einer teilweisen Entmischung führen, so dass sich schwerere Komponenten in den unteren Schichten und leichtere Komponenten in den höheren Schichten anreichern würden; die durch das Wettergeschehen bedingte intensive Durchmischung der Troposphäre verhindert dies jedoch. Der veränderliche Wasserdampfgehalt sowie verallgemeinert auch sonstige geringfügige Änderungen von M (vor allem in den höheren Atmosphärenschichten) kann durch Verwendung der entsprechenden virtuellen Temperatur $T_{v}$ anstelle der tatsächlichen Temperatur $T$ berücksichtigt werden. Für M kann daher der Wert für trockene Luft in Meereshöhe eingesetzt werden.

Geopotentielle Höhen

Die Schwerebeschleunigung $g$ nimmt mit der Höhe ab, was bei großen Höhendifferenzen oder hohen Genauigkeitsanforderungen berücksichtigt werden muss. Eine variable Schwerebeschleunigung im Integranden würde die Integration allerdings erheblich erschweren. Dies lässt sich umgehen durch Verwendung geopotentieller statt geometrischer Höhen. Man denke sich dazu eine Testmasse $m$ bei variablem $g$ von Meereshöhe auf die Höhe $h$ gehoben. Weil $g$ mit der Höhe abnimmt, ist die dabei gewonnene potentielle Energie $\Delta E_{\mathrm {pot} }$ kleiner als wenn $g$ stets den Meereshöhenwert $g_{0}$ hätte. Die geopotentielle Höhe $h_{p}$ ist die Höhe, gemessen in geopotentiellen Metern, die rechnerisch zu überwinden ist, um der Masse bei stets konstanter Schwerebeschleunigung $g_{0}$ dieselbe potentielle Energie $\Delta E_{\mathrm {pot} }$ zuzuführen (mit anderen Worten: $h_{p}$ ist das durch $g_{0}$ dividierte Schwerepotential. Flächen gleicher geopotentieller Höhe sind Äquipotentialflächen im Schwerefeld).

Für die zu einer geometrischen Höhe $h$ gehörige geopotentielle Höhe $h_{p}$ soll also gelten:

\Delta E_{\mathrm {pot} }=\int _{0}^{h}mg(h)\,\mathrm {d} h=mg_{0}\cdot h_{p}

,

woraus folgt:

g(h)\,\mathrm {d} h=g_{0}\,\mathrm {d} h_{p}

.

Für das Verhältnis der Schwerebeschleunigung $g$ in der Höhe $h$ zur Schwerebeschleunigung $g_{0}$ auf Meereshöhe gilt, da das Gravitationsfeld quadratisch mit dem Abstand zum Erdmittelpunkt abnimmt:

{\frac {g(h)}{g_{0}}}=\left({\frac {R_{\mathrm {E} }}{R_{\mathrm {E} }+h}}\right)^{2}

,

mit dem Erdradius $R_{\mathrm {E} }$ . Integration von

\mathrm {d} h_{p}={\frac {g(h)}{g_{0}}}\,\mathrm {d} h=\left({\frac {R_{\mathrm {E} }}{R_{\mathrm {E} }+h}}\right)^{2}\mathrm {d} h

liefert

\int _{0}^{h_{p}}\mathrm {d} h_{p}=\int _{0}^{h}\left({\frac {R_{\mathrm {E} }}{R_{\mathrm {E} }+h}}\right)^{2}\mathrm {d} h

\iff \ h_{p}={\frac {R_{\mathrm {E} }\cdot h}{R_{\mathrm {E} }+h}}

.

$R_{\mathrm {E} }$ ist dabei auf den Wert 6356 km zu setzen. Gegebenenfalls muss außerdem noch berücksichtigt werden, dass die Schwerebeschleunigung auf Meereshöhe $g_{0}$ von der geographischen Breite abhängt.

Auf diese Weise müssen nur einmal vor der Rechnung die gewünschten geometrischen Höhen in geopotentielle Höhen umgerechnet werden; in der Höhenformel kann dann statt der veränderlichen Schwerebeschleunigung einfach der konstante Meereshöhenwert verwendet werden. Für nicht zu große Höhen ist der Unterschied zwischen geometrischen und geopotentiellen Höhen gering und oft vernachlässigbar:

geometrisch	geopotentiell
0 m	0,0 m
500 m	500,0 m
1000 m	999,8 m
5000 m	4996,1 m
10000 m	9984,3 m

Mit der Schwerebeschleunigung auf Meereshöhe $g_{0}$ , den geopotentiellen Höhen $h_{p0}$ und $h_{p1}$ und der virtuellen Temperatur $T_{v}$ vereinfacht sich die allgemeine Höhenformel zu

p(h_{1})=p(h_{0})\cdot \exp \left(-{\frac {Mg_{0}}{R}}\int _{h_{p0}}^{h_{p1}}{\frac {1}{T_{v}(h_{p})}}\,\mathrm {d} h_{p}\right)

.

Es bleibt das Integral über $1/T_{v}$ zu lösen, wozu nur noch das Temperaturprofil $T_{v}(h_{p})$ bekannt sein muss. Es kann in der realen Atmosphäre zum Beispiel durch Radiosonden-Aufstiege bestimmt werden. Für vereinfachte Modellatmosphären mit konstanter oder linear veränderlicher Temperatur ergeben sich wieder Höhenformeln des eingangs behandelten Typs.

Anwendungen

Theorie

Der von einem Barometer gemessene Luftdruck (QFE) hängt vom meteorologischen Zustand der Atmosphäre und der Standorthöhe ab. Sollen die Angaben verschiedener Barometer für meteorologische Zwecke untereinander verglichen werden (zum Beispiel um die Lage eines Tiefdruckgebiets oder einer Front zu bestimmen), muss der Einfluss der Standorthöhen aus den Messdaten entfernt werden. Zu diesem Zweck werden die gemessenen Druckwerte auf eine gemeinsame Bezugshöhe, üblicherweise Meereshöhe, umgerechnet. Diese Umrechnung geschieht mittels einer Höhenformel. Das Umrechnen wird auch als Reduktion bezeichnet (auch wenn der Zahlenwert größer wird), da der Messwert dabei von unerwünschten Störeffekten befreit wird. Das Ergebnis ist der auf Meereshöhe reduzierte Luftdruck (QNH).

Je nach Genauigkeitsanforderungen muss eine geeignete Höhenformel benutzt werden. Bei geringeren Ansprüchen kann aus der Höhenformel für konstante Temperatur ein fester Umrechnungsfaktor abgeleitet werden, wozu eine repräsentative Temperatur zu wählen ist:

p_{0}=p(h)\,\mathrm {e} ^{{\frac {Mg}{RT}}h}

Für eine Standorthöhe von 500 m und bei Verwendung einer Jahresmitteltemperatur von 6 °C ergibt sich z. B. ein Reduktionsfaktor von 1,063, mit dem die gemessenen Werte zu multiplizieren sind.

Bei etwas höheren Ansprüchen kann die aktuelle Lufttemperatur berücksichtigt werden. Deren Einfluss zeigt folgendes Beispiel, in dem ein auf 500 m Höhe gemessener Luftdruck von 954,3 hPa mit der Höhenformel für linearen Temperaturverlauf (a = 0,0065 K/m) unter Annahme verschiedener Stationstemperaturen $T(h)$ auf Meereshöhe reduziert wird:

p_{0}=p(h)\,\left({\frac {T(h)}{T(h)+0{,}0065\mathrm {\frac {K}{m}} \,h}}\right)^{-5{,}255}=p(h)\,\left({\frac {T(h)}{T_{0}}}\right)^{-5{,}255}

$t(h)$	−10 °C	0 °C	10 °C	20 °C	30 °C
$p_{0}$	1017,9	1015,5	1013,3	1011,2	1009,3

T(h)=t(h)+273{,}15\,\mathrm {K}

Falls eine höhere Genauigkeit gewünscht ist, aktuelle Lufttemperaturen zur Verfügung stehen und Genauigkeit sowie Kalibrierung des verwendeten Barometers den Aufwand rechtfertigen, sollte die Reduktion stets unter Verwendung der aktuellen Lufttemperatur erfolgen. Als Höhenformel bietet sich die Variante für linearen Temperaturverlauf an. Es kann auch die Variante für konstanten Temperaturverlauf verwendet werden, sofern die auf halber Stationshöhe herrschende aktuelle Temperatur eingesetzt wird:

p_{0}=p(h)\,\mathrm {e} ^{{\frac {Mg}{R\,\left(T(h)+a{\frac {h}{2}}\right)}}h}

Diese Variante ist zwar theoretisch weniger genau, da sie die Veränderlichkeit der Temperatur mit der Höhe ignoriert, während die lineare Variante diese näherungsweise berücksichtigt. Bei den für Wetterstationen vorkommenden Höhen und Temperaturen sind die Unterschiede jedoch unbedeutend.

Die vom Deutschen Wetterdienst empfohlene Reduktionsformel entspricht der Variante mit konstantem Temperaturverlauf. Aus der auf Standorthöhe gemessenen Temperatur wird mit Hilfe des Standard-Temperaturgradienten die Temperatur auf halber Standorthöhe geschätzt. Die Luftfeuchte findet Berücksichtigung durch Übergang zur entsprechenden virtuellen Temperatur.[3]

p_{0}=p(h)\,\mathrm {e} ^{x},\quad x={\frac {g_{0}}{R^{*}\,(T(h)+C_{h}\cdot E+a{\frac {h}{2}})}}\,h

mit

$p_{0}$		Luftdruck auf Meeresniveau reduziert
$p(h)$		Luftdruck in Barometerhöhe (in hPa, auf 0,1 hPa genau)
$g_{0}$	= 9,80665 m/s²	Normfallbeschleunigung
$R^{*}$	= 287,05 m²/(s²K)	Gaskonstante trockener Luft (= R/M)
$h$		Barometerhöhe (in m, auf dm genau; bis 750 m Höhe kann mit der geometrischen Höhe gerechnet werden, darüber sind geopotenzielle Höhen zu verwenden)
$T(h)$		Hüttentemperatur (in K, wobei $T(h)=t(h)+273{,}15\,\mathrm {K}$ )
$t(h)$		Hüttentemperatur (in °C)
$a$	= 0,0065 K/m	vertikaler Temperaturgradient
$E$		Dampfdruck des Wasserdampfanteils (in hPa)
$C_{h}$	= 0,12 K/hPa	Beiwert zu $E$ zur Berücksichtigung der mittleren Dampfdruckänderung mit der Höhe (eigentlich stationsabhängig, hier als fester Mittelwert)

Falls keine gemessene Luftfeuchte zur Verfügung steht, kann $E$ auch gemäß folgender Approximation geschätzt werden, welche auf langjährigen Mittelwerten von Temperatur und Feuchte beruht:

t(h)<9{,}1\,^{\circ }\mathrm {C

t(h)\geq 9{,}1\,^{\circ }\mathrm {C

Praxis

Der Vergleich mehrerer Barometer macht die begrenzte absolute Genauigkeit handelsüblicher Geräte deutlich.

Die hier erhobenen Genauigkeitsanforderungen an gemessenen Luftdruck und Barometerhöhe werden für einen Amateurmeteorologen in der Regel nicht zu erfüllen sein. Bei den Barometern von Hobby-Wetterstationen wird durchaus mit systematischen Fehlern von mindestens 1 bis 2 hPa zu rechnen sein. Einer solchen Unsicherheit entspricht über die barometrische Höhenstufe eine Unsicherheit der Standorthöhe von zehn bis zwanzig Metern. Der Ehrgeiz, die Standorthöhe genauer bestimmen zu wollen, führt höchstwahrscheinlich nicht zu einem genaueren Ergebnis. In diesem Lichte wäre auch die Notwendigkeit oder Überflüssigkeit einer Berücksichtigung der Luftfeuchte zu betrachten.

Gegebenenfalls empfiehlt es sich, nicht die reale Standorthöhe zu verwenden, sondern eine fiktive Höhe, welche die beste Übereinstimmung des reduzierten Luftdrucks mit den Angaben eines nahe gelegenen Referenzbarometers (offizielle Wetterstation, Flughafen usw.) erzielt. Durch eine solche Kalibrierung lässt sich ein eventueller systematischer Fehler des Barometers größtenteils kompensieren. Hierzu ist es zweckmäßig, zunächst eine genäherte Höhe zur Reduktion zu verwenden und die eigenen Ergebnisse über einen längeren Zeitraum (vor allem auch bei verschiedenen Temperaturen) mit den Referenzangaben zu vergleichen. Wird ein systematischer Unterschied festgestellt, kann mit Hilfe einer geeigneten Höhenformel die Höhendifferenz berechnet werden, welche ausgehend von der genäherten Standorthöhe die reduzierten Höhen um den gewünschten Betrag verschiebt. Die auf diese Weise korrigierte Höhe wird dann für künftige Reduktionen verwendet. Wird die Temperatur bei der Reduktion nicht berücksichtigt, sollte beim Kalibrieren die Situation bei einer repräsentativen Temperatur zugrunde gelegt werden.

Ein typisches Wohnzimmerbarometer

Einfache Wohnzimmerbarometer werden in der Regel so eingestellt, dass sie unmittelbar den reduzierten Luftdruck anzeigen. Meist geschieht dies durch eine Schraube auf der Gehäuserückseite, mit der sich die Vorspannung der Druckdosenfeder ändern lässt. Die Kalibrierung entspricht also einer Verschiebung der Anzeigeskala. Das ist streng genommen nicht korrekt. Wie die Höhenformeln zeigen, muss die Reduktion durch Multiplikation mit einem Kalibrierfaktor erfolgen und nicht durch bloße Addition einer Konstanten: Der reduzierte Luftdruck ändert sich um etwas mehr als ein hPa, wenn sich der Luftdruck auf Standorthöhe um ein hPa ändert. Die Skala müsste also zusätzlich zur Verschiebung auch leicht gestreckt werden. Der dadurch verursachte Fehler ist jedoch geringer als der Fehler, der dadurch entsteht, dass diese Geräte den Temperatureinfluss auf die Reduktion ignorieren. Da sie keine Eingabemöglichkeit für die Standorthöhe haben, kann eine Kalibrierung nur durch Vergleich mit einem Referenzbarometer erfolgen, wodurch wiederum gleichzeitig systematische Nullpunktfehler des Instruments vermindert werden. Die Kalibrierung muss für den Standort des Barometers (oder einen Ort vergleichbarer Höhe) erfolgen. Es hat keinen Zweck, das Gerät beim Händler „richtig einstellen“ zu lassen, wenn es dann an einem völlig anderen Ort aufgehängt wird. Wenn das Barometer dazu dient, aus Luftdruckänderungen eine kurzfristige Wettervorhersage abzuleiten, ist eine genaue Kalibrierung weniger wichtig.

Grenzen

Generell ist bei der Reduktion von Luftdruckmessungen zu bedenken, dass die dabei rechnerisch addierte Luftsäule für die meisten Standorte in Wirklichkeit nicht existieren kann und es daher auch keinen „wahren“ Wert für den „Meereshöhendruck am Standort“ geben kann, der durch hinreichend aufwendiges Rechnen präzise angenähert werden könnte. Die Reduktionsformeln beruhen zum Teil lediglich auf Konventionen und dienen, abgesehen von speziellen wissenschaftlichen Anwendungen, hauptsächlich dazu, die Messwerte der Wetterstationen so weit wie möglich untereinander vergleichbar zu machen. Ein Beispiel zur Fiktivität der addierten Luftsäule: Über ebenem Gelände, auf dem kalte Luft nicht abfließt, kann sich in klaren Nächten wegen der Wärmeabstrahlung des Erdbodens die bodennahe Luft merklich abkühlen (Bodeninversion). Eine dort befindliche Wetterstation wird diese verringerte Temperatur registrieren und mit dem üblichen Temperaturgradienten rechnerisch nach unten fortsetzen. Befände sich das Gelände aber auf Meereshöhe, so wäre jene Luft wegen des nun fehlenden Erdbodens gar nicht abgekühlt und die nun tatsächlich existierende Luftsäule hätte eine deutlich höhere Temperatur als die rechnerische. Die Rechnung hat also eine zu hohe Dichte der addierten Luftsäule angenommen und ergibt einen höheren reduzierten Luftdruck, als er bei derselben Wetterlage herrschen würde, falls das gesamte Gelände auf Meereshöhe läge.

Barometrische Höhenmessung

Die Höhenabhängigkeit des Luftdrucks kann auch zur Höhenmessung verwendet werden. Barometrische Höhenmessungen sind schnell und relativ einfach durchzuführen, in ihrer Genauigkeit jedoch begrenzt. Ein für die Höhenbestimmung ausgelegtes Barometer bezeichnet man als Höhenmesser oder Altimeter. Die Vorgehensweise richtet sich nach Verwendungszweck und Genauigkeitsansprüchen. Anwendung findet das Verfahren unter anderem beim Wandern und mit etwas höheren Genauigkeitsansprüchen in der Landvermessung.

Literatur

Richard Rühlmann: Die barometrischen Höhenmessungen und ihre Bedeutung für die Physik der Atmosphäre. Leipzig 1870, S. 10–12, 21–24 (digital). (zur Geschichte)

W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 3. Auflage. Springer-Verlag, Berlin / Heidelberg / New York 2000, ISBN 3-540-67180-3.

Siehe auch

Höhe über dem Meeresspiegel

Weblinks

Wikibooks: Formelsammlung Hydrostatik – Lern- und Lehrmaterialien

Online-Rechenprogramm für die Internationale Höhenformel

Einzelnachweise

Edmond Halley: A discourse of the rule of the decrease of the height of the mercury in the barometer. In: Philos. Transactions, 1686 and 1687, Bd. 16, S. 104
K.-H. Ahlheim [Hrsg.]: Wie funktioniert das? Wetter und Klima. Meyers Lexikonverlag, Mannheim/Wien/Zürich 1989, ISBN 3-411-02382-1, S. 46
Deutscher Wetterdienst (Hrsg.): Beobachterhandbuch (BHB) für Wettermeldestellen des synoptisch-klimatologischen Mess- und Beobachtungsnetzes (= Vorschriften und Betriebsunterlagen. Nr. 3). Dezember 2015, Kap. 6.6 Reduktion des Luftdrucks (Volltext [PDF; 3,4 MB; abgerufen am 24. Januar 2022]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Edmond Halley: A discourse of the rule of the decrease of the height of the mercury in the barometer. In: Philos. Transactions, 1686 and 1687, Bd. 16, S. 104

[2] K.-H. Ahlheim [Hrsg.]: Wie funktioniert das? Wetter und Klima. Meyers Lexikonverlag, Mannheim/Wien/Zürich 1989, ISBN 3-411-02382-1, S. 46

[BHB-3] Deutscher Wetterdienst (Hrsg.): Beobachterhandbuch (BHB) für Wettermeldestellen des synoptisch-klimatologischen Mess- und Beobachtungsnetzes (= Vorschriften und Betriebsunterlagen. Nr. 3). Dezember 2015, Kap. 6.6 Reduktion des Luftdrucks (Volltext [PDF; 3,4 MB; abgerufen am 24. Januar 2022]).