Archytas von Tarent

Archytas von Tarent (griechisch Ἀρχύτας Archýtas; * wohl zwischen 435 und 410 v. Chr.; † wohl zwischen 355 und 350 v. Chr.) war ein antiker griechischer Philosoph, Mathematiker, Musiktheoretiker, Physiker, Ingenieur, Staatsmann und Feldherr.

Archytas wirkte in seiner Heimatstadt, der griechischen Kolonie Tarent in Apulien. Als Philosoph gehörte er zur Richtung der Pythagoreer. Bekannt ist er vor allem durch seine freundschaftliche Beziehung zu Platon, durch die angeblich von ihm erfundene fliegende Taube und durch ein Gedankenexperiment, mit dem er die Unendlichkeit des Universums beweisen wollte. Von seinen Schriften, die insbesondere Themen der Mathematik und der Musik behandelten, sind nur wenige Fragmente erhalten geblieben.

Als Wissenschaftstheoretiker war Archytas Optimist. Er meinte, wissenschaftliche Erkenntnis sei leicht zu gewinnen, wenn man über die richtige Methode verfüge. Besonderes Gewicht legte er auf die Mathematik als Grundlagenwissenschaft. Seine bedeutendste mathematische Leistung war die Lösung des Problems der Verdoppelung des Würfels. Sie zeigt, dass er über eine für seine Zeit außergewöhnliche methodische Komplexität verfügte. Zur musikalischen Harmonielehre trug er mit seiner mathematischen Theorie harmonischer Intervalle bei. In der Optik versuchte er für die Spiegelung und in der Akustik für die unterschiedlichen Tonhöhen eine Erklärung zu finden. Seine wissenschaftlichen Leistungen, von denen wegen der Spärlichkeit der überlieferten Angaben nur wenig bekannt ist, fanden in der antiken Nachwelt und bei modernen Wissenschaftshistorikern Anerkennung.

Eine maßgebliche Rolle spielte Archytas politisch und militärisch als leitender Staatsmann und Stratege seiner Heimatstadt und eines von ihr geführten Bundes griechischer Kolonien Süditaliens. Seine militärischen Erfolge verschafften ihm hohe Autorität. Innenpolitisch setzte er sich für sozialen Ausgleich ein, wobei er es für möglich hielt, ein Gerechtigkeitskonzept wissenschaftlich zu begründen und damit Konsens herbeizuführen.

Leben

Der Vater des Philosophen hieß wahrscheinlich Hestiaios. Nach anderen, weniger glaubwürdigen Angaben war sein Name Mnesagoras, Mnasagetes oder Mnesarchos. Ansonsten ist über die Herkunft des Archytas nichts bekannt. Seine Geburt lässt sich nur ungefähr datieren; sie fällt wohl in die Zeit zwischen 435 und 410 v. Chr.[1] Offenbar war seine Familie reich; die anekdotische Überlieferung zeigt ihn als Großgrundbesitzer.[2]

Wissenschaft

Cicero berichtet, der philosophische Lehrer des Archytas sei Philolaos von Kroton gewesen.[3] Das ist plausibel, aber nicht sicher.[4] Philolaos gehörte der Richtung der Pythagoreer an, die sich auf die Lehren des Pythagoras von Samos beriefen. Nach Angaben des römischen Schriftstellers Valerius Maximus[5] erhielt Archytas eine lange, gründliche Ausbildung in Metapont, einem traditionellen Zentrum des Pythagoreismus. Dort hatte im 6. Jahrhundert v. Chr. Pythagoras gelebt und gelehrt. Archytas fügte sich in die pythagoreische Tradition ein, doch das bedeutet nicht, dass er von ihr eine Dogmatik übernahm. Im 4. Jahrhundert v. Chr. wurde er in erster Linie als eigenständiger Denker wahrgenommen, der an Themen und Ideen der Pythagoreer anknüpfte. Aristoteles unterschied klar zwischen den Auffassungen des Archytas und denen der „sogenannten“ Pythagoreer, mit denen er sich separat auseinandersetzte. – Von den Schülern des Archytas sind nur der Mathematiker Eudoxos von Knidos und ein Archedemos, den Platon schätzte, namentlich bekannt.[6]

Politische und militärische Aktivität

Tarent hatte ab ungefähr 473 v. Chr. eine demokratische Verfassung,[7] stand aber im Peloponnesischen Krieg (431–404 v. Chr.) auf der Seite Spartas, dessen Mischverfassung von monarchischen und aristokratisch-oligarchischen Elementen geprägt war, und stellte sich damit gegen das demokratische Athen. Sparta war die Mutterstadt von Tarent, das einst von spartanischen Kolonisten gegründet worden war. Syrakus, die Vormacht im griechisch besiedelten Teil Siziliens, zählte ebenfalls zu den schließlich siegreichen Feinden Athens. Nach dem Ende des Krieges nahm Tarent eine freundliche Haltung gegen Syrakus ein und hielt sich aus den militärischen Auseinandersetzungen zwischen dem Tyrannen Dionysios I. von Syrakus und einer 393 gebildeten Liga süditalischer Griechenstädte heraus. Nachdem der Tyrann 379/378 die führende Stadt der Liga, Kroton, erobert hatte, übernahm Tarent die Führung der Liga, wohl im Einvernehmen mit Dionysios, und entwickelte sich zur Führungsmacht im festländischen Teil der Magna Graecia, der griechisch besiedelten Teile Siziliens und des süditalischen Festlands. Nun begann eine Blütezeit der Stadt. In diese Periode, die siebziger und sechziger Jahre des 4. Jahrhunderts v. Chr., fiel die politisch-militärische Glanzzeit des Archytas, der bereits eine vorteilhafte Ausgangslage vorfand und dann die Gunst der Verhältnisse zu nutzen wusste. Militärisch war Tarent damals eine regionale Großmacht, es war etwa so stark wie Athen vor dem Ausbruch des Peloponnesischen Krieges und verfügte über eine bedeutende Flotte. Nach Angaben, die Strabon überliefert, konnte die Stadt 30.000 Infanteristen und 4000 Kavalleristen aufbieten.[8]

Der Aktionsraum des Archytas. Für Tarent ist der griechische Name Taras angegeben.

Die Umstände von Archytas’ Aufstieg zu einer führenden Stellung sind nicht dokumentiert. Sicher ist jedenfalls, dass er sich militärisch auf außergewöhnliche Weise bewährte. Der kaiserzeitliche Philosophiegeschichtsschreiber Diogenes Laertios, der sich wahrscheinlich auf Angaben des gut informierten Philosophen Aristoxenos stützte, hob rühmend hervor, dass Archytas als Einziger siebenmal von seinen Mitbürgern zum Feldherrn (Strategos) gewählt wurde, obwohl das Gesetz keine Wiederwahl nach dem Ende der einjährigen Amtszeit zuließ.[9] Gemeint war wohl, dass er siebenmal hintereinander einem Kollegium von gewählten Feldherren angehörte, obwohl unmittelbare Wiederwahl verboten war, da man einer gefährlichen Machtkonzentration vorbeugen wollte. Offenbar wurde die gesetzliche Vorschrift durch einen Volksbeschluss eigens für Archytas außer Kraft gesetzt. Diese Sonderregelung illustriert das außerordentliche Vertrauen, dessen er sich erfreute. Als Befehlshaber besaß er Sondervollmachten, die mit seinem Titel strategós autokrátor verbunden waren; er durfte wohl militärische Entscheidungen nach eigenem Ermessen fällen, unterstand aber letztlich der Aufsicht der Volksversammlung seiner Mitbürger. Einmal legte er das Feldherrnamt nieder, angeblich infolge von Machenschaften neidischer Gegner; darauf erlitten die Tarentiner prompt eine Niederlage, womit seine Unersetzlichkeit bewiesen war.[10]

Als führender Staatsmann und Stratege Tarents war Archytas zugleich Oberkommandierender der Streitkräfte der Liga. Deren Zweck war hauptsächlich der gemeinsame Kampf der griechischen Siedler gegen ihre traditionellen Gegner, die einheimischen Italiker, gegen die Tarent schon im 5. Jahrhundert v. Chr. mit wechselndem Erfolg vorgegangen war. Die Feldzüge des Archytas gegen die Italiker waren alle erfolgreich.[11]

Verhältnis zu Platon

Zur Bekanntheit des Archytas in späterer Zeit trug vor allem seine Beziehung zu Platon bei. Den später berühmten athenischen Philosophen lernte er kennen, als dieser bei seiner ersten Italienreise (388/387 v. Chr.), bevor er Dionysios I. in Syrakus aufsuchte, einen Aufenthalt in Tarent einlegte. Archytas wurde Gastfreund (xénos) des Atheners. Platon war wohl in erster Linie an Archytas’ Mathematikkenntnissen interessiert, weniger an seinen philosophischen Ansichten. Das Gastfreundschaftsverhältnis beinhaltete gegenseitige Verpflichtungen zu beiderseitigem Vorteil, war aber nicht notwendigerweise mit einer engen persönlichen Freundschaft verbunden. Die späte Überlieferung, der zufolge Platon von Archytas philosophische Erkenntnisse erhoffte oder sogar sein Schüler wurde, ist nicht vertrauenswürdig.[12] Unglaubwürdig ist auch eine späte Legende, der zufolge Platon auf Befehl des syrakusischen Tyrannen versklavt und von Archytas gekauft und freigelassen wurde.[13]

Für die weitere Entwicklung ist Platons siebter Brief die Hauptquelle. Die Authentizität des Briefs ist zwar in der Forschung seit langem umstritten, aber seine Schilderung des Ablaufs der Ereignisse gilt als glaubwürdig, auch falls er nicht von Platon stammt. Jedenfalls war der Autor mit den Verhältnissen vertraut. Nach der Darstellung im Brief hat Platon während seines zweiten Sizilienaufenthalts (366–365 v. Chr.), als er auf den Tyrannen Dionysios II. von Syrakus, den Sohn und Nachfolger Dionysios’ I., Einfluss gewann, eine freundschaftliche Verbindung zwischen Archytas und dem jungen syrakusischen Herrscher hergestellt. Später, nach Platons Abreise, besuchte Archytas den Tyrannen. Während seines Aufenthalts in Syrakus pflegte der tarentinische Staatsmann nicht nur die politische Beziehung, sondern belehrte Dionysios II. anscheinend auch philosophisch und erhielt einen positiven Eindruck von ihm. In der Folgezeit bedrängten sowohl die Tarentiner als auch Dionysios den nach Athen heimgekehrten Platon, er solle sich nochmals auf den Weg machen, trotz der Verstimmung, die während des zweiten Aufenthalts zwischen ihm und dem Tyrannen eingetreten war. Von Platons Einfluss auf Dionysios erhoffte sich Archytas eine Stabilisierung des guten Verhältnisses zwischen Tarent und dem syrakusischen Reich. Durch die dringenden Bitten aus Syrakus und Tarent ließ sich der alte Philosoph zu seiner dritten Sizilienreise (361–360 v. Chr.) überreden. Diesmal fiel er aber bei dem Tyrannen in Ungnade, wurde in politische Konflikte verwickelt und geriet in Lebensgefahr. Dem siebten Brief zufolge gelang es ihm, Archytas von seiner Notlage zu benachrichtigen, worauf die Tarentiner eine Gesandtschaft schickten, die zu seinen Gunsten intervenierte und dem bedrängten Philosophen die Erlaubnis zur Abreise verschaffte.[14]

Tod

Wahrscheinlich starb Archytas im Zeitraum zwischen 355 und 350 v. Chr. Nach seinem Tod setzte in Tarent ein Niedergang ein, der schließlich dazu führte, dass sich die Tarentiner ab etwa 340 v. Chr. nicht mehr auf die eigenen militärischen Ressourcen verließen, sondern Söldnerführer anheuerten, die fortan einen bedeutenden Anteil an der Kriegführung hatten.[15]

In Ode I,28 (Te maris et terrae) des römischen Dichters Horaz wird Archytas im Zusammenhang mit einem Schiffbrüchigen angesprochen, der um seine Bestattung bittet. Daraus wurde verschiedentlich geschlossen, er sei bei einem Schiffbruch in der Adria ums Leben gekommen.[16] Diese Deutung ist umstritten.[17]

Früher irrtümlich als Archytas identifizierte Büste im Archäologischen Nationalmuseum Neapel

Bildliche Darstellung

Bildnisse eines Mannes mit turbanartiger Kopfbedeckung – eine bronzene Büste im Archäologischen Nationalmuseum von Neapel und eine römische Herme im Museo Capitolino in Rom – sind wegen des eigentümlichen Haarstils als Darstellungen des Archytas identifiziert worden, da diese Haartracht auch auf einer entsprechend beschrifteten Münze von Tarent zu sehen ist. Die Münze hat sich jedoch als moderne Fälschung erwiesen, womit die Grundlage für die Identifizierung entfällt.[18]

Werke

Von den Werken des Archytas sind nur vier sicher echte Fragmente erhalten. In den älteren Quellen findet sich keine Werkliste. In späterer Zeit waren viele unechte Werke unter seinem Namen im Umlauf.[19] Die ursprünglichen Titel der authentischen Werke sind nicht bekannt, die diesbezüglichen Angaben der zitierenden antiken Autoren gelten als unzuverlässig. Sicher ist nur, dass Musik und Mathematik behandelt wurden. Für eine der Schriften wird der Titel Über die Wissenschaften in verschiedenen Varianten (Perí mathematikón, Perí mathemáton, Peri mathematikés) genannt. Eine andere – oder möglicherweise ein Teil von Über die Wissenschaften – hieß vielleicht Harmonik. Ein weiteres Werk, das angeblich den Titel Abhandlungen (diatribaí) trug, beinhaltete möglicherweise den Versuch, der Ethik eine wissenschaftliche Grundlage zu geben. Vielleicht verfasste Archytas auch Schriften über Kosmologie, Biologie, Maschinen und Landwirtschaft.[20]

Philosophie

Obwohl Archytas ein jüngerer Zeitgenosse des Sokrates war, den er um Jahrzehnte überlebte, wird er zu den Vorsokratikern gezählt, weil er zu einer älteren Tradition gehörte, die noch nicht unter dem Einfluss der sokratischen Philosophie stand. Diese Zuordnung ist jedoch problematisch, denn seine Werke entstanden erst nach dem Tod des Sokrates.[21]

Archytas betrachtete die „Zahlenwissenschaft“, die er logistikē nannte, als Grundlage der Wissenschaften und betonte auch ihren Vorrang vor der Geometrie. In der Hochschätzung der Mathematik stimmte er mit Platon überein. Während jedoch Platon in der Beschäftigung mit Mathematik nur eine Vorbereitung auf das Studium der Philosophie sah und sein Bildungsverständnis auf ein rein geistiges Erfassen der Wirklichkeit abzielte, teilte Archytas Platons Geringschätzung der Empirik nicht und machte auch die scharfe platonische Trennung zwischen den Bereichen des geistig Erkennbaren und des sinnlich Wahrnehmbaren nicht mit. Für ihn war die Arithmetik auch unter politischem Gesichtspunkt wichtig, weil sie ihm die Möglichkeit zu bieten schien, einleuchtende Formeln für eine einvernehmliche, ausgewogene Besitzverteilung unter den Bürgern zu finden. Da die Anwendung solcher Formeln für jeden überprüfbar war, konnte damit nach Archytas’ Überzeugung der soziale Frieden hergestellt und bewahrt werden. Dies war in den oft von blutigen Machtkämpfen erschütterten griechischen Städten von größter Bedeutung. Ein Ausgleich zwischen den sozialen Schichten, der gewaltsamen Konflikten (stáseis) in der Bürgerschaft vorbeugen sollte, war ein zentrales Anliegen des Archytas. Die Verwirklichung erwartete er von der richtigen, angemessenen „Berechnung“ (logismós), die nachweislich gewährleiste, dass niemand übervorteilt werde.[22]

Bruno Snell weist auf den Bedeutungswandel des Wortes máthema hin, das der Grundbedeutung nach das bezeichnet, was gelernt ist oder gelernt werden kann. Als Bezeichnung für Wissenschaft ist dieser Ausdruck erstmals bei Archytas bezeugt. Für den Tarentiner Philosophen nahm zwar unter den Wissensgebieten das eigentlich Mathematische die Zentralstellung ein, doch neben Geometrie und Arithmetik gehörten auch Astronomie und Musik zu den mathémata. Diese vier Wissenschaften nannte Archytas „verschwistert“. Erst später wurde das Bedeutungsfeld auf Mathematik eingeengt, weil nur noch die Mathematik als Wissenschaft im eigentlichen Sinne erschien, denn nur sie schien der Forderung zu entsprechen, dass die Gegenstände einer Wissenschaft mit völliger Sicherheit erkennbar sein müssen.[23]

Anscheinend entwickelte Archytas eine Wissenschaftstheorie als Lehre, in der er die Kunst des richtigen Suchens – die wissenschaftliche Vorgehensweise – als Grundvoraussetzung für den Erfolg behandelte.[24] Er bekannte sich zu einem erkenntnistheoretischen Optimismus; nach seiner Überzeugung sind Entdeckungen leicht und einfach, wenn man über die richtige Methode verfügt.[25] Die Einzelheiten seiner Methode sind wegen der ungünstigen Quellenlage schwer zu ermitteln. Überliefert ist sein Grundsatz, dass man zunächst gute Unterscheidungen hinsichtlich der Beschaffenheit der „Ganzen“ treffen müsse; wenn dies gelungen sei, könne man die Natur der Einzelobjekte gut erfassen. Demnach schreitet die wissenschaftliche Erkenntnis vom Allgemeineren zum Spezielleren voran. Was genau er mit den „Ganzen“ meinte – etwa die allgemeinen Konzepte einer bestimmten Wissenschaft – geht aus den spärlichen Angaben der Quellen nicht hervor.[26] Jedenfalls war Archytas der Überzeugung, dass eigenes Entdecken von Sachverhalten dem Übernehmen von bereits vorhandenem Wissensstoff überlegen sei. Was man selbst herausgefunden habe, sei etwas Eigenes (ídion); das Wissensgut, das man sich lernend aneigne, sei etwas Fremdes.[27]

In der Ethik legte Archytas besonderes Gewicht auf die Forderung, man solle sich stets nach der Vernunft richten und niemals spontan aus Ärger handeln oder sich von Begierden den Verstand vernebeln lassen.[28]

Kosmologie

Die Überlieferung, wonach sich Archytas auch als Astronom betätigte, geht auf die römischen Dichter Horaz und Properz zurück, die wohl keine zuverlässigen Informationen darüber besaßen. Authentisch und berühmt ist jedoch seine Argumentation für die Unendlichkeit des Universums. Es handelt sich um ein Gedankenexperiment, das besagt: Wenn jemand, der an einem angenommenen Ende des Universums angekommen wäre, dort seine Hand oder einen Stab ausstrecken würde, müsste er entweder auf einen Körper oder auf leeren Raum stoßen, also auf jeden Fall auf eine Fortsetzung des Universums. Somit muss der Kosmos unendlich ausgedehnt sein. Dieser Gedanke wurde von den Stoikern und Epikureern und noch von John Locke und Isaac Newton aufgegriffen und abgewandelt.[29]

Mathematik

Irrationalität

Archytas befasste sich mit den in damaliger Ausdrucksweise „überteilig“ genannten Verhältnissen $(n+1):n$ . Das sind Verhältnisse $a:b$ , bei denen der „Überschuss“ von $a$ über $b$ der n-te Teil von $b$ ist und dann gilt: $a:b=(n+1):n$ .[30] Archytas fand einen Beweis für den Satz „Zwischen zwei Zahlen in einem überteiligen Verhältnis können niemals mittlere Proportionale (geometrische Mittel) gefunden werden.“ Das bedeutet in moderner Terminologie, dass es irrationale Größenverhältnisse gibt, die sich nicht als rationale Zahlenverhältnisse (Bruchzahlen) darstellen lassen. Die Quadratwurzeln ${\sqrt {(n+1):n}}$ sind irrational.[31]

Kurve des Archytas

Kurve des Archytas

Der Vorgang der Würfelverdoppelung

Hippokrates von Chios war es gelungen, das Problem der Verdopplung des Würfels auf ein Verhältnisproblem zurückzuführen: Es genüge, für die Strecke $a$ , die Kante des zu verdoppelnden Würfels, die Strecken $u$ und $v$ so zu finden – das bedeutet: geometrisch zu konstruieren –, dass sie im Verhältnis $a:u=u:v=v:2a$ stehen. Dann ist nämlich

\left({\frac {a}{u}}\right)^{3}={\frac {a}{u}}\times {\frac {u}{v}}\times {\frac {v}{2a}}={\frac {a}{2a}}={\frac {1}{2}}.

Es gilt also

2\times a^{3}=u^{3}

und der Würfel mit der Kante $u$ ist wie gewünscht eine Verdopplung des Würfels mit der Kante $a$ .

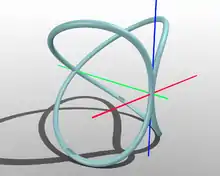
Es gelang Hippokrates jedoch nicht, $u$ und $v$ für vorgegebene Strecken $a$ und $b$ so zu konstruieren, dass $a:u=u:v=v:b$ gilt, auch nicht für den hier allein benötigten Spezialfall $b=2a$ . Darum bemühten sich spätere antike Wissenschaftler. Der spätantike Mathematiker Eutokios überliefert in seinem Kommentar zur Abhandlung Peri sphaíras kai kylíndrou (Über Kugel und Zylinder) des Archimedes zwölf Lösungen. Deren früheste und beste ist die des Archytas. Sie gelang ihm mit Hilfe der daher nach ihm benannten Kurve. Diese ist die erste krumme – das heißt in keiner Ebene enthaltene – Kurve, die in der Geschichte der Mathematik benutzt wurde. Die Konstruktion, mit der ein Schnittpunkt dreier gekrümmter Oberflächen gefunden wird, ist in der antiken Mathematik einzigartig und vor allem für dieses frühe Stadium der Mathematikgeschichte erstaunlich. Dennoch wird in der heutigen Forschung überwiegend angenommen, dass sie tatsächlich von Archytas stammt.[32]

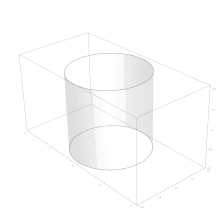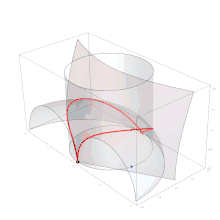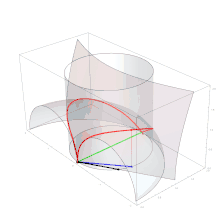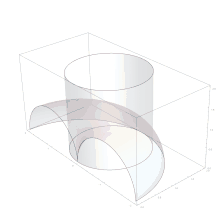
Zur Lösung benutzte Archytas die Oberflächen dreier Körper: eines Torus, eines Zylinders und eines Konus. In moderner Darstellung mittels geeignet gewählter kartesischer Koordinaten werden diese Oberflächen jeweils durch eine der folgenden Gleichungen gegeben:

{\begin{matrix}x^{2}+y^{2}+z^{2}=a{\sqrt {x^{2}+y^{2}}}\\x^{2}+y^{2}=ax\\x^{2}+y^{2}+z^{2}={\frac {a^{2}}{b^{2}}}x^{2}\end{matrix}}

Torus und Zylinder schneiden sich in der Kurve des Archytas. Der Schnittpunkt $P$ dieser Kurve mit dem Konus ist ein Punkt, der allen drei Gleichungen genügt. Für ihn gilt also, wenn abkürzend

u={\sqrt {x^{2}+y^{2}+z^{2}}}

und

v={\sqrt {x^{2}+y^{2}}}

geschrieben wird:

\left\{{\begin{matrix}u^{2}=av\\v^{2}=ax\\u^{2}={\frac {a^{2}}{b^{2}}}x^{2}\end{matrix}}\right.

Die erste Gleichung besagt $a:u=u:v$ . Wenn in der dritten für $ax$ das laut der zweiten Gleichung gleichwertige $v^{2}$ eingesetzt wird, ergibt sich nach Wurzelziehen und Umstellung $u:v=v:b$ . Insgesamt gilt also die gewünschte Beziehung $a:u=u:v=v:b$ . Die Strecke von $P$ zum Koordinatenursprung hat die Länge $u$ ; so wurde $u$ eingeführt. Sie ist also im Fall $b=2a$ die Kante des verdoppelten Würfels. Eine Rekonstruktion von Archytas’ Vorgehen gibt Stephen Menn.[33] Die Konstruktion gelingt nicht, wenn nur Zirkel und Lineal verwendet werden dürfen; diese Forderung wurde aber erst nach Archytas in der griechischen Mathematik vorherrschend.

Musik

Der von Archytas bewiesene Satz, dass es zwischen den Zahlen $n+1$ und $n$ , die in „überteiligem“ Verhältnis stehen, kein geometrisches Mittel geben kann, hat für die Harmonik die Konsequenz, dass es unmöglich ist, die grundlegenden harmonischen Intervalle – die Oktave (2:1), die Quinte (3:2), die Quarte (4:3) und den Ganzton (9:8) – durch eine mittlere Proportionale in zwei gleiche Teile zu teilen. Daher teilte Archytas die Quinte und die Quarte mit Hilfe der arithmetischen und harmonischen Mittel. Auf diese Verhältnisse gestützt entwickelte er eine mathematische Theorie harmonischer Intervalle für alle drei zu seiner Zeit verwendeten Tetrachorde (das enharmonische, das chromatische und das diatonische Tongeschlecht). Die Zahlenverhältnisse der Intervalle innerhalb der Tetrachorde bestimmte er, jeweils mit dem höchsten Ton beginnend, für das diatonische Tongeschlecht als 9:8, 8:7, 28:27, für das chromatische als 32:27, 243:224; 28:27 und für das enharmonische als 5:4, 36:35, 28:27. In der Musikpraxis ging es dabei um die zwei inneren Saiten eines viersaitigen Instruments, die „beweglichen“ Saiten, die in den drei Tongeschlechtern verschieden gestimmt wurden.[34]

Die Arbeit des Archytas wurde im weiteren Verlauf der antiken musiktheoretischen Forschung fortgesetzt. Ein Ergebnis dieser Bemühungen waren die Befunde in Euklids Sectio canonis. Der inhaltliche Zusammenhang zwischen den Studien des Archytas und der Sectio canonis hat manche moderne Forscher zur Annahme bewogen, dass Euklids Werk im Wesentlichen einen Text des Tarentiners wiedergebe. Gegen diese Vermutung wird aber vorgebracht, dass die Unterschiede gewichtiger seien als die Übereinstimmungen. Immerhin kann Archytas jedenfalls als Vorläufer betrachtet werden.[35]

Physik

Optik

Der kaiserzeitliche Schriftsteller Apuleius, der sich vermutlich auf glaubwürdige Angaben des Archimedes stützte, erwähnte in seiner Apologia eine optische Theorie des Archytas zur Erklärung der Spiegelungen.[36] Das Phänomen des Spiegelns wurde in der Antike unterschiedlich gedeutet. Nach einer der Hypothesen sendet jedes Ding ständig Atome aus, die, wenn sie die Augen der Sehenden erreichen, ihnen die Gestalt des Objekts übermitteln, von dem sie stammen. Demnach beruht Spiegelung darauf, dass die spiegelnde Fläche die Atome zurückwirft. Einer alternativen Hypothese zufolge sendet das Auge beim Sehen Strahlen aus, die mit den Objekten der Außenwelt Kontakt aufnehmen und beim Spiegeln reflektiert werden. Archytas zählte wie Platon zu den Befürwortern der zweiten Erklärung. Seine Auffassung unterscheidet sich aber beträchtlich von der Platons. Während Platon meinte, dass die vom Auge ausgehenden Strahlen nur im Zusammenwirken mit äußerem Licht einen optischen Eindruck erzeugen können, glaubte Archytas, dass sie keine solche Unterstützung benötigen. Wie er unter dieser Voraussetzung erklären konnte, dass bei äußerer Dunkelheit nichts sichtbar ist, ist unbekannt; er muss einen äußeren hindernden Faktor angenommen haben.[37]

Für die Pythagoreer war die mathematische Optik eines der wichtigsten Forschungsfelder. Es ging ihnen darum, den Sehvorgang durch geometrische Beziehungen zu beschreiben. Wer von ihnen die mathematischen Optik begründet hat, ist unbekannt; in der wissenschaftsgeschichtlichen Forschung wird vermutet, dass Archytas eine Pionierrolle spielte.[38]

Akustik

Archytas legte eine Theorie der Akustik vor, wobei er sich auf Ergebnisse nicht namentlich genannter früherer Forscher berief, die er für schlüssig hielt. Damit meinte er anscheinend einen damals bestehenden Konsens der Forschung. Seine Argumentation stützte er auf „Experimente“ sowie auf Erfahrungen mit der menschlichen Stimme und mit der Funktionsweise von Musikinstrumenten. Unter Experimenten verstand er nicht nur Versuchsanordnungen im modernen Sinn, sondern auch allgemein Beobachtungen aller Art, insbesondere alltägliche Erfahrungen. In den akustischen Phänomenen sah er nicht Erzeugnisse des Wahrnehmungsapparats des Hörenden, sondern objektive Tatsachen, die auch gegeben sind, wenn niemand hört. Somit ist nach seinem Verständnis ein Geräusch auch dann als solches aufzufassen, wenn es außerhalb des Wahrnehmungsspektrums von Hörenden liegt, etwa weil es zu leise ist. Als Bedingung für die Entstehung von Geräuschen nannte er, offenbar einem damaligen Konsens folgend, die Einwirkung bewegter Dinge, die zusammenstoßen, aufeinander. Für den Umstand, dass manche Geräusche gehört werden und andere nicht, gab er drei Gründe an, die nach seinen Worten in der menschlichen Natur liegen: Wenn man einen Klang nicht hört, ist entweder der Zusammenstoß der erzeugenden Dinge zu schwach oder die Distanz zur Geräuschquelle zu groß oder das Geräusch so laut, dass es wegen seiner Stärke nicht wahrgenommen werden kann. Der letztgenannte Fall tritt ein, wenn das Geräusch so voluminös ist, dass es nicht in den engen Gehörgang passt und daher nicht ins Ohr eindringen kann. Solche Geräusche sind somit prinzipiell unhörbar. Offenbar betrachtete Archytas den Klang als eine Art Materie, die sich durch den Raum bewegt und dabei auch ins Ohr gelangt, sofern sie hineinpasst. Ob er mit den extrem lauten und daher unhörbaren Klängen die Sphärenharmonie – die angeblich von den Himmelskörpern erzeugten Töne – meinte, ist unklar.[39]

Die Erklärung des Archytas für die unterschiedlichen Tonhöhen der hörbaren Klänge lautet: Hohe Töne sind die, die mit relativ hoher Geschwindigkeit aufs Ohr treffen; je langsamer ein Ton bei seinem Eintreffen ist, desto tiefer erscheint er dem Hörenden. Diese Theorie ist vor Archytas nicht bezeugt, sie stammt wahrscheinlich von ihm. Dafür spricht der Umstand, dass er seine Hypothese ausführlich begründete, offenbar weil er es für erforderlich hielt, das Publikum von einer neuen Idee zu überzeugen. Die lauten und leisen Töne verglich er mit mehr oder weniger kraftvoll abgeschossenen oder geschleuderten Wurfwaffen, die nur dann weit fliegen und mit Wucht auftreffen, wenn sie einen starken Impuls erhalten haben. Zur Veranschaulichung wies Archytas auch darauf hin, dass man sich beim lauten Sprechen oder Singen anstrengen muss, um mit kraftvoller Stimme die gewünschte Lautstärke zu erzeugen. Des Weiteren führte er an, dass bei einem Blasinstrument der erzeugte Ton dann tiefer ist, wenn der Schall bei gleicher Kraft des Blasens eine längere Strecke durch das Rohr zurückzulegen hat. Diesen Effekt führte er auf eine Abschwächung der Bewegung durch die größere Distanz zurück. In seiner Theorie fehlt allerdings noch eine Unterscheidung zwischen den voneinander unabhängigen Ursachen von Tonhöhe und Lautstärke; die Aspekte, die er nennt – Geschwindigkeit und Wucht des Auftreffens –, haben dieselbe Ursache. Die Differenzierung der Kausalität leistete erst die spätere antike Forschung. – Die Vorstellung des Archytas, dass die Tonhöhe von der variierenden Geschwindigkeit des Schalls abhängt, setzte sich in der Folgezeit in der antiken Akustik allgemein durch. Allerdings widersprach ihr Theophrast.[40]

In moderner Terminologie besagt die Feststellung des Archytas, dass die Lautstärke, die Amplitude, von der Energie abhängt, die dem Schall von seiner Quelle mitgeteilt wurde, und dass die Strecke, die der Schall zurücklegt, bis er zur Unhörbarkeit gedämpft wird, bei größerer Amplitude länger ist. Der Ansatz, die Tonhöhe auf Geschwindigkeit zurückzuführen, war richtig, nur nahm Archytas irrtümlich an, es sei die Geschwindigkeit, mit der sich der Schall fortpflanzt. In Wirklichkeit ist es die Frequenz, die Schnelligkeit der Schwingung, das heißt die Anzahl der Hin- und Herbewegungen pro Zeiteinheit.[41]

Mechanik

Archytas galt lange als Begründer der Mechanik. Dafür gibt es aber keinen Beweis, wenn man mit dem Begriff Mechanik die Vorstellung von Ingenieurwesen als angewandter Wissenschaft verbindet. Nach den Angaben des Diogenes Laertios hat Archytas als Erster die Mechanik unter Heranziehung mathematischer Prinzipien methodisch behandelt.[42] Demnach hat er als Pionier einen Beitrag zur Theorie geleistet; für die Anwendung besagt das nichts. Plutarch behauptete, Archytas und Eudoxos von Knidos seien die ersten Wissenschaftler gewesen, die sich mit Mechanik und Technik beschäftigt hätten. Sie hätten mit mechanischen Apparaturen Probleme wie die Würfelverdoppelung gelöst, die theoretisch und zeichnerisch schwer zu lösen seien. Platon habe jedoch diese Vorgehensweise als unmathematisch kritisiert und ihr damit ein Ende gesetzt.[43] Dies trifft aber nach heutigem Forschungsstand auf Archytas nicht zu, denn sein Verfahren der Würfelverdoppelung war rein abstrakt, es wurden keine Instrumente eingesetzt. Somit entfallen die Belege für seine Rolle als Begründer des praktischen Ingenieurwesens. Von den Apparaten, deren Erfindung Archytas zugeschrieben wurde, stammen nur zwei tatsächlich von ihm: die fliegende „Taube des Archytas“ und wahrscheinlich auch eine Klapper. Die Klapper ist aber nur ein Spielzeug, und die Taube macht Archytas nicht zum Begründer einer angewandten Ingenieurwissenschaft. Er war nur einer der wichtigen Vorläufer, welche die Voraussetzungen für die Entstehung dieses Wissenszweigs schufen. Für die Behauptungen, er habe den Flaschenzug erfunden und Kriegsmaschinen ersonnen, fehlen Belege. Zwar war Archytas anscheinend grundsätzlich an der Anwendung mathematischer Erkenntnisse auf physikalische Objekte interessiert, aber es lässt sich nicht zeigen, dass er über abstrakte Überlegungen hinausging.[44]

Taube des Archytas

Von der Taube berichtet Aulus Gellius, ein römischer Schriftsteller des 2. Jahrhunderts. Er beruft sich auf eine heute verlorene griechische Schrift seines älteren Zeitgenossen Favorinus, die er zitiert, und auf Angaben weiterer, nicht namentlich genannter Autoren. Nach dieser Darstellung konstruierte Archytas eine hölzerne Nachbildung einer Taube, die mittels einer von ihm ersonnenen Mechanik fliegen konnte. Dazu bemerkt Gellius, dies scheine unglaublich, sei aber für wahr zu halten. Die Konstruktion sei durch Gegengewichte (libramenta) balanciert worden. Die Taube sei durch eine verborgene, eingeschlossene Luftströmung in Bewegung gesetzt worden. Allerdings konnte sie sich laut dem Favorinus-Zitat nach der Landung nicht erneut in die Luft erheben.[45]

Als Erfinder des Geräts wird bei Gellius und Favorinus Archytas von Tarent bezeichnet. In der Forschung wird aber die Möglichkeit erwogen, dass eine Verwechslung mit einem gleichnamigen Autor vorliegt, der in späterer Zeit eine Abhandlung über Mechanik verfasste.[46]

In der Fachliteratur sind verschiedene Erklärungshypothesen erörtert worden, deren Ausgangsbasis ein 1904 von Wilhelm Schmidt dargelegtes Modell bildet. Diesem zufolge flog die Taube nicht frei, sondern war Bestandteil eines größeren Apparats, für den Rollen benötigt wurden. Eine Schnur verband sie mit dem in der Luft hängenden Gegengewicht. Der hölzerne Vogel war hohl, mit Pressluft gefüllt und mit einem verborgenen Ventil versehen, durch dessen Öffnung Luft entweichen konnte. Dadurch verringerte sich das Gewicht, und das Gegengewicht, das so schwer war wie die Taube samt der komprimierten Luft, erlangte das Übergewicht und senkte sich, so dass die Taube emporgeschnellt wurde.[47] Carl A. Huffman hat eine abgewandelte Version des Modells vorgelegt, die ohne die Annahme von Pressluft in der Taube auskommt; nach seiner Deutung wurde der benötigte Luftstrom außerhalb des Vogels erzeugt.[48] Karin Luck-Huyse vermutet „eine Art Strahlantrieb mittels komprimierter Luft“.[49]

Klapper

Der zweite Apparat, den Archytas anscheinend erfand, ist eine Klapper (griechisch platagḗ). Aristoteles berichtet, die „Klapper des Archytas“ sei für unruhige Kinder bestimmt; ihr Zweck sei, kleinere Kinder zu beschäftigen und von unerwünschten Tätigkeiten abzuhalten.[50] Der Ausdruck wurde sprichwörtlich: Von einer Person, die sich nicht ruhig halten kann, wurde gesagt, sie benötige eine Klapper des Archytas. Einer anekdotischen Überlieferung zufolge zeigte Archytas besonderes Interesse an Kindern und spielte gern mit ihnen. Daher scheint es plausibel, dass er tatsächlich ein derartiges Gerät ersonnen hat. Es ist aber auch möglich, dass der Erfinder ein gleichnamiger Architekt war. Wie die Klapper aussah, ist unbekannt; es dürfte sich um ein Gerät in der Art von Kastagnetten gehandelt haben.[51]

Rezeption

Antike und Mittelalter

Aristoteles setzte sich intensiv mit der Philosophie des Archytas auseinander. Er behandelte sie in einer besonderen Schrift aus drei Büchern. Außerdem verfasste er eine Gegenüberstellung von Platons Dialog Timaios und der Schriften des Archytas. Beide Werke des Aristoteles sind heute verloren. Sein Schüler Aristoxenos, der aus Archytas’ Heimatstadt Tarent stammte, schrieb eine Biographie seines berühmten Landsmanns, die ebenfalls verloren ist. Aristoxenos, der als jüngerer Zeitgenosse des Archytas gut informiert war, verwertete anekdotisches Material und gab eine wohlwollende Darstellung. Auf dieser Lebensbeschreibung fußt wohl ein großer Teil der späteren biographischen und doxographischen Tradition, darunter die kurze Archytas-Biographie des Diogenes Laertios.[52]

Unter dem Namen des Archytas sind eine Reihe von Abhandlungen und Fragmenten sowie zwei Briefe in dorischem Dialekt überliefert, die sicher nicht von ihm stammen, sondern von verschiedenen unbekannten Autoren. Sie gehören zum pseudepigraphen (unter falschen Verfassernamen verbreiteten) philosophischen Schrifttum, dessen anonyme Autoren ihre Schriften bekannten Pythagoreern der Vergangenheit zuschrieben, um damit ihren literarischen Fiktionen Beachtung zu verschaffen. Unter den Pythagoreern ist Archytas derjenige, unter dessen Namen in der Antike die meisten derartigen Werke kursierten. Die Datierung der pseudo-archyteischen Schriften ist umstritten; nach einer älteren Forschungsmeinung (Holger Thesleff) gehören sie großenteils in die frühhellenistische Zeit, nach den heute vorherrschenden Datierungsansätzen sind manche im 1. Jahrhundert v. Chr. oder im 1. Jahrhundert n. Chr. entstanden. Behandelt werden Fragen der Logik, Erkenntnistheorie, Metaphysik, Ethik und Staatstheorie.[53]

In der Antike kursierte eine Reihe von Anekdoten, die für die gebildete Öffentlichkeit das Bild des berühmten Philosophen und Staatsmanns prägten. Die Frage nach einem historischen Kern des Erzählguts bleibt offen. Markante Motive waren Archytas’ Kinderfreundlichkeit sowie seine Selbstbeherrschung und Rationalitätsforderung; so wurde erzählt, er habe es grundsätzlich abgelehnt, im Zorn zu strafen, und habe lieber auf eine eigentlich nötige Bestrafung verzichtet, als sie unter dem Einfluss der Emotion auszuführen. Ferner wurde ihm eine von Cicero überlieferte Äußerung über den sozialen Charakter des Menschen zugeschrieben: Wenn jemand zum Himmel emporsteigen und von dort aus die Beschaffenheit und Schönheit des Kosmos wahrnehmen könnte, so würde er zwar darüber staunen, könnte diese Bewunderung der Welt aber nicht genießen, wenn niemand da wäre, mit dem er sie teilen könnte. Dieses angebliche Archytas-Zitat verwertete Cicero für seinen Lobpreis der Freundschaft.[54]

Cicero ließ in seinem literarischen Dialog Cato maior de senectute den römischen Staatsmann Marcus Porcius Cato Censorius auftreten. In dem fiktiven, ins Jahr 150 v. Chr. gesetzten Dialog berichtet Cato von seinem Aufenthalt in Tarent im Jahr 209 v. Chr. Damals erfuhr er nach seinen Worten als Gast eines einheimischen Pythagoreers von einer Rede des Archytas, deren Inhalt sein Gastgeber ihm gemäß einer lokalen mündlichen Überlieferung mitteilte. Die Dialogfigur Cato befindet, Archytas sei „mit an erster Stelle unter die großen, hervorragenden Männer zu rechnen“.[55]

Horaz pries in einer seiner Oden die wissenschaftlichen Leistungen des Archytas. In dem Gedicht erscheint der Tarentiner als der, „der Länder und Meer und des Sandes unzählbare Menge ausmaß“, die Himmelsräume erforschte und im Geist das Weltall durchflog. Mit dem Ausmessen ist die Geometrie gemeint, mit der Erkundung des Weltalls wohl das Argument für die Unendlichkeit des Kosmos.[56]

Mit dem religiösen Aspekt der pythagoreischen Tradition wurde Archytas erst in der Spätantike in Verbindung gebracht. Im Mittelalter wurde er dann als einer der großen Weisen der Antike und auch als Magier dargestellt.[57]

Frühe Neuzeit

Im 16. und 17. Jahrhundert faszinierte der Bericht des Gellius über die fliegende Taube des Archytas die Gelehrten, die neue technische Errungenschaften erhofften. Der antike Wissenschaftler wurde als Pionier der Mechanik gefeiert. Athanasius Kircher und Gaspar Schott, die ebenso wie ihr Zeitgenosse René Descartes Tiere als Maschinen betrachteten, hielten es für grundsätzlich möglich, eine fliegende Taube zu konstruieren. Ihre Versuche, das Geheimnis des Archytas zu ergründen, blieben jedoch erfolglos.[58]

Als vorbildlicher Weiser und Staatsmann tritt Archytas in der ersten Fassung von Christoph Martin Wielands Roman Geschichte des Agathon (1766–1767) auf. Der aus Athen stammende Protagonist Agathon begibt sich nach einer wechselvollen Karriere nach Syrakus, wo er in einem politischen Kampf unterliegt und ins Gefängnis geworfen wird. Zur Rettung wird ihm seine alte Freundschaft mit Archytas’ Sohn Critolaus. Archytas, der als weiser Staatsmann und Gesetzgeber die Republik Tarent lenkt, sorgt für Agathons Freilassung, und Critolaus bewegt ihn zur Übersiedlung nach Tarent. Wieland schildert die tarentinische Republik als idyllisches Staatswesen, als die paradiesische, utopisch wirkende Welt des Archytas, die „mehr durch die Macht der Sitten als durch das Ansehen der Gesetze“ ihren idealen gesellschaftlichen Zustand bewahrt. Archytas, jetzt ein ehrwürdiger Greis, hat sich dank seiner maßvollen, vernünftigen Lebensweise die „Lebhaftigkeit aller Kräfte“ bewahrt, die in seinem Alter etwas Seltenes ist. Seinen Erfolg und seine Autorität als allseits bewunderter und geliebter Staatslenker verdankt Wielands Archytas vor allem seinem ausgeglichenen, harmonischen Naturell. Von der Tyrannei der Leidenschaften, den „Verirrungen des Geistes und des Herzens“, hat er sich stets ferngehalten, und metaphysische Spekulationen, die über die Grenzen des menschlichen Verstandes hinausgehen, überlässt er seinem Freund Platon. Seine Philosophie ist ganz praktisch; sie beschränkt sich auf die Wahrheiten, „welche das allgemeine Gefühl erreichen kann“ und die Vernunft bekräftigt.[59] Mit der Stimmigkeit ihres Lebens verwirklicht die Romanfigur Archytas ein wichtiges Anliegen Wielands, doch distanziert sich dieser ausdrücklich von seiner eigenen Idylle: Er tritt als unschuldiger Herausgeber auf, der die erzählte Geschichte nur einem alten griechischen Manuskript entnommen habe, und kritisiert den fiktiven Autor, der sich im letzten Teil seines Werks in eine Wunderwelt, „in das Land der schönen Seelen, und der utopischen Republiken“ verirrt habe.[60] – In der dritten, umgearbeiteten Fassung von 1794 baute Wieland den Schlussteil des Romans aus, wobei er insbesondere der Rolle des Archytas größeres Gewicht gab.[61]

Moderne

In der modernen wissenschaftsgeschichtlichen Forschung haben Archytas’ Leistungen große Anerkennung erfahren, wenngleich bei vielen Annahmen betont wird, dass sie wegen der ungünstigen Quellenlage unsicher sind. Pierre Wuilleumier, der 1939 eine umfangreiche Monographie zur Geschichte und Kultur des griechischen Tarent veröffentlichte, beschrieb Archytas als innovatives Genie, als dominierende Gestalt der Politik und des Geisteslebens seiner Heimatstadt und ihrer Region und als „das erste und schönste Beispiel eines Philosophen an der Macht“.[62] Maria Timpanaro Cardini (1962) rühmte die „Modernität“ seiner Einstellung, die Breite seines Interessenspektrums, die Klarheit seines Denkens und seine konsequent wissenschaftliche Vorgehensweise.[63] Walter Burkert (1962) stellte fest, Archytas habe die Bahn zu einer allgemeinen Zahlentheorie, wie sie dann bei Euklid vorliegt, eingeschlagen. Er habe seine Zahlentheorie, die aus der Musiktheorie herausgewachsen sei, „mit den Beweismethoden der hochentwickelten Geometrie aus spekulativer Zahlen- und Musiklehre“ geschaffen und die Musiktheorie zahlentheoretisch ausgebaut. Die Würfelverdoppelung bezeichnete Burkert als bahnbrechend.[64] Myles Frederic Burnyeat (2005) sah in Archytas einen brillanten Mathematiker und den Begründer der mathematischen Optik,[65] Leonid Zhmud (2013) würdigte ihn als „das seltene Beispiel eines hervorragenden Mathematikers und originellen Denkers, der gleichzeitig ein erfolgreicher Staatsmann war“.[66]

Kritischer fiel das Urteil von Bartel Leendert van der Waerden (1956) aus. Er würdigte die Vielseitigkeit und den Ideenreichtum des antiken Wissenschaftlers, dessen Denken ganz kinematisch gewesen sei, und hob hervor, „wie lebendig seine Raumanschauung und seine Bewegungsvorstellungen waren“. Andererseits bemängelte van der Waerden jedoch Weitschweifigkeit der Darlegungen und konstatierte einen „merkwürdigen Gegensatz zwischen seinen genialen Ideen, seiner schöpferischen Phantasie, seiner großartigen Beherrschung der geometrischen Methoden einerseits und seiner mangelhaften Logik, seinem Unvermögen, sich genau und klar auszudrücken, seinen Denkfehlern und Umständlichkeiten andererseits“.[67] Dieser Einschätzung widersprach Carl A. Huffman, der 2005 eine große Monographie über Archytas mit Edition der Fragmente und Testimonien vorlegte. Er wies insbesondere die Behauptung zurück, der Stil des Archytas sei unklar und sein Diskurs logisch fehlerhaft.[68] Huffmans Standardwerk, die erste Monographie über den Tarentiner seit 1840, prägt seit seinem Erscheinen den Gang der Forschung.

Der Mondkrater Archytas und der Asteroid (14995) Archytas sind nach dem antiken Wissenschaftler benannt, ebenso die Pflanzengattung Archytaea Mart. 1824 aus der Familie der Bonnetiaceae.[69]

Textausgabe

Carl A. Huffman: Archytas of Tarentum. Pythagorean, Philosopher and Mathematician King. Cambridge University Press, Cambridge 2005, ISBN 0-521-83746-4 (grundlegende Studie; enthält Ausgabe der Fragmente mit englischer Übersetzung und ausführlichem Kommentar und Zusammenstellung aller übrigen Quellenzeugnisse)

Literatur

George C. Brauer: Taras. Its History and Coinage. Caratzas, New Rochelle 1986, ISBN 0-89241-377-8, S. 43–59
Bruno Centrone: Archytas de Tarente. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Band 1, CNRS, Paris 1989, ISBN 2-222-04042-6, S. 339–342
Charles H. Kahn: Pythagoras and the Pythagoreans. A Brief History. Hackett, Indianapolis 2001, ISBN 0-87220-576-2
Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Schwabe, Basel 2013, ISBN 978-3-7965-2598-8, S. 425–428

Weblinks

Commons: Archytas von Tarent – Sammlung von Bildern, Videos und Audiodateien

Literatur zu Archytas und Pseudo-Archytas im Katalog der Deutschen Nationalbibliothek
Eintrag in Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.

Anmerkungen

Siehe dazu Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 6; Bernard Mathieu: Archytas de Tarente, pythagoricien et ami de Platon. In: Bulletin de l’Association Guillaume Budé, Jg. 1987, S. 239–255, hier: 240.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 18; George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 45 f.
Cicero, De oratore 3,34,139.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 7, 34, 46; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 181.
Valerius Maximus, Facta et dicta memorabilia 4,1,ext.1.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 6–8. Vgl. zur Eigenständigkeit des Archytas als Philosoph Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 176 f.
George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 27 f. und Anm. 5; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 17 f.
George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 31, 43–45; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 5, 9–11; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 62–66.
Diogenes Laertios 8,79.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 10–14; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 68–71.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 9–14; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 70–73.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 32–35, 37, 41; Bernard Mathieu: Archytas de Tarente, pythagoricien et ami de Platon. In: Bulletin de l’Association Guillaume Budé, Jg. 1987, S. 239–255, hier: 246 f.; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 182 f.
Alice Swift Riginos: Platonica, Leiden 1976, S. 90 f.
Siebter Brief 338c–340a. Siehe dazu Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 32–42; Geoffrey Lloyd: Plato and Archytas in the Seventh Letter. In: Phronesis 35, 1990, S. 159–174, hier: 162 f., 165–168, 172 f.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 5 f.; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 77 f. Vgl. George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 61–63.
Ross S. Kilpatrick: Archytas at the Styx (Horace Carm. 1. 28). In: Classical Philology 63, No. 3 (1968), S. 201–206; Gerhard Fink (Hrsg. und Übers.): Q. Horatius Flaccus. Oden und Epoden. Sammlung Tusculum, Artemis & Winkler, Düsseldorf/Zürich 2002, ISBN 978-3-11-036002-8, S. 382 f. (abgerufen über De Gruyter Online).
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 19–21; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 74 f.
Richard Neudecker: Die Skulpturenausstattung römischer Villen in Italien (= Beiträge zur Erschließung hellenistischer und kaiserzeitlicher Skulptur und Architektur. Band 9). Philipp von Zabern, Mainz 1988, S. 148 Nr. 14.3; Bruno Centrone, Marie-Christine Hellmann: Archytas de Tarente. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Bd. 1, Paris 1989, S. 339–342, hier: 342; Gisela M. A. Richter: The Portraits of the Greeks, Bd. 2, London 1965, S. 179 (vgl. Bd. 1, London 1965, S. 79).
Ein Verzeichnis bietet Holger Thesleff: An Introduction to the Pythagorean Writings of the Hellenistic Period, Åbo 1961, S. 8–11.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 30–32, 187 f., 228–232; Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 299 f.; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 179 f.
Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 297.
Christoph Riedweg: Pythagoras, 2., überarbeitete Auflage, München 2007, S. 146; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 68–76, 190–193; Bernard Mathieu: Archytas de Tarente, pythagoricien et ami de Platon. In: Bulletin de l’Association Guillaume Budé, Jg. 1987, S. 239–255, hier: 253; Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 309–312.
Bruno Snell: Die Ausdrücke für den Begriff des Wissens in der vorplatonischen Philosophie, 2. Auflage, Hildesheim/Zürich 1992, S. 76–80.
Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 427 f.
Leonid Zhmud: The Origin of the History of Science in Classical Antiquity, Berlin 2006, S. 68.
Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 302–309.
Siehe dazu Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 312.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 24, 283–290, 323–337.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 22–24, 541–550; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 186 f.
Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 373, 406.
Siehe dazu Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 457–470.
Stephen Menn: How Archytas Doubled the Cube. In: Brooke Holmes, Klaus-Dietrich Fischer (Hrsg.): The Frontiers of Ancient Science, Berlin 2015, S. 407–435, hier: 407 f.; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 184 f. Anderer Meinung ist allerdings Luc Brisson: Archytas and the duplication of the cube. In: Gabriele Cornelli u. a. (Hrsg.): On Pythagoreanism, Berlin 2013, S. 203–233, hier: 213–222.
Stephen Menn: How Archytas Doubled the Cube. In: Brooke Holmes, Klaus-Dietrich Fischer (Hrsg.): The Frontiers of Ancient Science, Berlin 2015, S. 407–435, hier: 409–434.
Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 16 f.; Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 427.
Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 427; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 130.
Apuleius, Apologia 15.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 550–556.
Myles Frederic Burnyeat: Archytas and Optics. In: Science in Context 18, 2005, S. 35–53. Vgl. Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 567 f.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 129–138.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 138–148; Alan C. Bowen: The Foundations of Early Pythagorean Harmonic Science: Archytas, Fragment 1. In: Ancient Philosophy 2, 1982, S. 79–104, hier: 92 f.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 140, 144.
Diogenes Laertios 8,83.
Plutarch, Marcellus 14.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 77–83.
Aulus Gellius, Noctes Atticae 10,12,9 f.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 571.
Wilhelm Schmidt: Aus der antiken Mechanik. In: Neue Jahrbücher für das Klassische Altertum 13, 1904, S. 329–351, hier: 349–351.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 570–579.
Karin Luck-Huyse: Der Traum vom Fliegen in der Antike, Stuttgart 1997, S. 133.
Aristoteles, Politik 1340b25–31.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 302–307.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 3–5.
Übersichten bieten Bruno Centrone: Pseudo-Archytas. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Bd. 1, Paris 1989, S. 342–345 und Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 595–609.
Cicero, Laelius de amicitia 23,88. Vgl. Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 18 f., 283–290, 293–296.
Cicero, Cato maior de senectute 12,39. Zur Frage der Herkunft des Inhalts siehe Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 324–331; Federico Russo: L’incontro tra Archita, Platone e Ponzio Sannita in Cic. Cato 12, 39–41. In: Mediterraneo Antico 10, 2007, S. 433–445.
Horaz, Oden 1,28. Vgl. Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 21–24.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 4, 25.
Anthony Grafton: Conflict and Harmony in the Collegium Gellianum. In: Leofranc Holford-Strevens, Amiel Vardi (Hrsg.): The Worlds of Aulus Gellius, Oxford 2004, S. 318–342, hier: 338–342.
Christoph Martin Wieland: Geschichte des Agathon. Erste Fassung, herausgegeben von Fritz Martini, Stuttgart 1985, S. 558–567.
Christoph Martin Wieland: Geschichte des Agathon. Erste Fassung, herausgegeben von Fritz Martini, Stuttgart 1985, S. 552–557.
Walter Erhart: »Geschichte des Agathon«. In: Jutta Heinz (Hrsg.): Wieland-Handbuch, Stuttgart/Weimar 2008, S. 259–274, hier: 262 f., 266–272.
Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 67, 584.
Maria Timpanaro Cardini (Hrsg.): Pitagorici. Testimonianze e frammenti, Band 2, Florenz 1962, S. 262.
Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 364, 423, 425.
Myles Frederic Burnyeat: Archytas and Optics. In: Science in Context 18, 2005, S. 35–53, hier: 33.
Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 425.
Bartel Leendert van der Waerden: Erwachende Wissenschaft, Basel/Stuttgart 1956, S. 247–249, 252 f.
Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 468–470.
Lotte Burkhardt: Verzeichnis eponymischer Pflanzennamen – Erweiterte Edition. Teil I und II. Botanic Garden and Botanical Museum Berlin, Freie Universität Berlin, Berlin 2018: Online-Fundstelle.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Siehe dazu Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 6; Bernard Mathieu: Archytas de Tarente, pythagoricien et ami de Platon. In: Bulletin de l’Association Guillaume Budé, Jg. 1987, S. 239–255, hier: 240.

[2] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 18; George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 45 f.

[3] Cicero, De oratore 3,34,139.

[4] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 7, 34, 46; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 181.

[5] Valerius Maximus, Facta et dicta memorabilia 4,1,ext.1.

[6] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 6–8. Vgl. zur Eigenständigkeit des Archytas als Philosoph Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 176 f.

[7] George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 27 f. und Anm. 5; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 17 f.

[8] George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 31, 43–45; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 5, 9–11; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 62–66.

[9] Diogenes Laertios 8,79.

[10] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 10–14; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 68–71.

[11] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 9–14; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 70–73.

[12] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 32–35, 37, 41; Bernard Mathieu: Archytas de Tarente, pythagoricien et ami de Platon. In: Bulletin de l’Association Guillaume Budé, Jg. 1987, S. 239–255, hier: 246 f.; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 182 f.

[13] Alice Swift Riginos: Platonica, Leiden 1976, S. 90 f.

[14] Siebter Brief 338c–340a. Siehe dazu Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 32–42; Geoffrey Lloyd: Plato and Archytas in the Seventh Letter. In: Phronesis 35, 1990, S. 159–174, hier: 162 f., 165–168, 172 f.

[15] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 5 f.; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 77 f. Vgl. George C. Brauer: Taras. Its History and Coinage, New Rochelle 1986, S. 61–63.

[16] Ross S. Kilpatrick: Archytas at the Styx (Horace Carm. 1. 28). In: Classical Philology 63, No. 3 (1968), S. 201–206; Gerhard Fink (Hrsg. und Übers.): Q. Horatius Flaccus. Oden und Epoden. Sammlung Tusculum, Artemis & Winkler, Düsseldorf/Zürich 2002, ISBN 978-3-11-036002-8, S. 382 f. (abgerufen über De Gruyter Online).

[17] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 19–21; Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 74 f.

[18] Richard Neudecker: Die Skulpturenausstattung römischer Villen in Italien (= Beiträge zur Erschließung hellenistischer und kaiserzeitlicher Skulptur und Architektur. Band 9). Philipp von Zabern, Mainz 1988, S. 148 Nr. 14.3; Bruno Centrone, Marie-Christine Hellmann: Archytas de Tarente. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Bd. 1, Paris 1989, S. 339–342, hier: 342; Gisela M. A. Richter: The Portraits of the Greeks, Bd. 2, London 1965, S. 179 (vgl. Bd. 1, London 1965, S. 79).

[19] Ein Verzeichnis bietet Holger Thesleff: An Introduction to the Pythagorean Writings of the Hellenistic Period, Åbo 1961, S. 8–11.

[20] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 30–32, 187 f., 228–232; Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 299 f.; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 179 f.

[21] Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 297.

[22] Christoph Riedweg: Pythagoras, 2., überarbeitete Auflage, München 2007, S. 146; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 68–76, 190–193; Bernard Mathieu: Archytas de Tarente, pythagoricien et ami de Platon. In: Bulletin de l’Association Guillaume Budé, Jg. 1987, S. 239–255, hier: 253; Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 309–312.

[23] Bruno Snell: Die Ausdrücke für den Begriff des Wissens in der vorplatonischen Philosophie, 2. Auflage, Hildesheim/Zürich 1992, S. 76–80.

[24] Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 427 f.

[25] Leonid Zhmud: The Origin of the History of Science in Classical Antiquity, Berlin 2006, S. 68.

[26] Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 302–309.

[27] Siehe dazu Andrew Barker: Archytas Unbound. In: Oxford Studies in Ancient Philosophy 31, 2006, S. 297–321, hier: 312.

[28] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 24, 283–290, 323–337.

[29] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 22–24, 541–550; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 186 f.

[30] Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 373, 406.

[31] Siehe dazu Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 457–470.

[32] Stephen Menn: How Archytas Doubled the Cube. In: Brooke Holmes, Klaus-Dietrich Fischer (Hrsg.): The Frontiers of Ancient Science, Berlin 2015, S. 407–435, hier: 407 f.; Monte Ransome Johnson: Sources for the Philosophy of Archytas. in: Ancient Philosophy 28, 2008, S. 173–199, hier: 184 f. Anderer Meinung ist allerdings Luc Brisson: Archytas and the duplication of the cube. In: Gabriele Cornelli u. a. (Hrsg.): On Pythagoreanism, Berlin 2013, S. 203–233, hier: 213–222.

[33] Stephen Menn: How Archytas Doubled the Cube. In: Brooke Holmes, Klaus-Dietrich Fischer (Hrsg.): The Frontiers of Ancient Science, Berlin 2015, S. 407–435, hier: 409–434.

[34] Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 16 f.; Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 427.

[35] Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 427; Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 130.

[36] Apuleius, Apologia 15.

[37] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 550–556.

[38] Myles Frederic Burnyeat: Archytas and Optics. In: Science in Context 18, 2005, S. 35–53. Vgl. Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 567 f.

[39] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 129–138.

[40] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 138–148; Alan C. Bowen: The Foundations of Early Pythagorean Harmonic Science: Archytas, Fragment 1. In: Ancient Philosophy 2, 1982, S. 79–104, hier: 92 f.

[41] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 140, 144.

[42] Diogenes Laertios 8,83.

[43] Plutarch, Marcellus 14.

[44] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 77–83.

[45] Aulus Gellius, Noctes Atticae 10,12,9 f.

[46] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 571.

[47] Wilhelm Schmidt: Aus der antiken Mechanik. In: Neue Jahrbücher für das Klassische Altertum 13, 1904, S. 329–351, hier: 349–351.

[48] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 570–579.

[49] Karin Luck-Huyse: Der Traum vom Fliegen in der Antike, Stuttgart 1997, S. 133.

[50] Aristoteles, Politik 1340b25–31.

[51] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 302–307.

[52] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 3–5.

[53] Übersichten bieten Bruno Centrone: Pseudo-Archytas. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Bd. 1, Paris 1989, S. 342–345 und Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 595–609.

[54] Cicero, Laelius de amicitia 23,88. Vgl. Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 18 f., 283–290, 293–296.

[55] Cicero, Cato maior de senectute 12,39. Zur Frage der Herkunft des Inhalts siehe Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 324–331; Federico Russo: L’incontro tra Archita, Platone e Ponzio Sannita in Cic. Cato 12, 39–41. In: Mediterraneo Antico 10, 2007, S. 433–445.

[56] Horaz, Oden 1,28. Vgl. Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 21–24.

[57] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 4, 25.

[58] Anthony Grafton: Conflict and Harmony in the Collegium Gellianum. In: Leofranc Holford-Strevens, Amiel Vardi (Hrsg.): The Worlds of Aulus Gellius, Oxford 2004, S. 318–342, hier: 338–342.

[59] Christoph Martin Wieland: Geschichte des Agathon. Erste Fassung, herausgegeben von Fritz Martini, Stuttgart 1985, S. 558–567.

[60] Christoph Martin Wieland: Geschichte des Agathon. Erste Fassung, herausgegeben von Fritz Martini, Stuttgart 1985, S. 552–557.

[61] Walter Erhart: »Geschichte des Agathon«. In: Jutta Heinz (Hrsg.): Wieland-Handbuch, Stuttgart/Weimar 2008, S. 259–274, hier: 262 f., 266–272.

[62] Pierre Wuilleumier: Tarente des origines à la conquête romaine, Paris 1939, S. 67, 584.

[63] Maria Timpanaro Cardini (Hrsg.): Pitagorici. Testimonianze e frammenti, Band 2, Florenz 1962, S. 262.

[64] Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 364, 423, 425.

[65] Myles Frederic Burnyeat: Archytas and Optics. In: Science in Context 18, 2005, S. 35–53, hier: 33.

[66] Leonid Zhmud: Archytas aus Tarent (DK 47). In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 1), Halbband 1, Basel 2013, S. 425–428, hier: 425.

[67] Bartel Leendert van der Waerden: Erwachende Wissenschaft, Basel/Stuttgart 1956, S. 247–249, 252 f.

[68] Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 468–470.

[Burkhardt2018-69] Lotte Burkhardt: Verzeichnis eponymischer Pflanzennamen – Erweiterte Edition. Teil I und II. Botanic Garden and Botanical Museum Berlin, Freie Universität Berlin, Berlin 2018: Online-Fundstelle.