Spieltheorie
Die Spieltheorie ist eine mathematische Theorie, in der Entscheidungssituationen modelliert werden, in denen mehrere Beteiligte miteinander interagieren. Sie versucht dabei unter anderem, das rationale Entscheidungsverhalten in sozialen Konfliktsituationen davon abzuleiten. Die Spieltheorie ist originär ein Teilgebiet der Mathematik. Sie bedient mannigfaltige Anwendungsfelder.
In diesem Artikel wird die nicht-kooperative Spieltheorie behandelt, die von der kooperativen Spieltheorie zu unterscheiden ist. Unten finden sich einige Bemerkungen zu den Unterschieden.
Begriff und Abgrenzung
Ein Spiel im Sinne der Spieltheorie ist eine Entscheidungssituation mit mehreren Beteiligten, die sich mit ihren Entscheidungen gegenseitig beeinflussen. Im Unterschied zur klassischen Entscheidungstheorie modelliert diese Theorie also Situationen, in denen der Erfolg des Einzelnen nicht nur vom eigenen Handeln, sondern auch von dem anderer abhängt (interdependente Entscheidungssituation).
Der Begriff Spieltheorie (engl. game theory) entstand aus zuvor von den Begründern verwendeten Begriffsumschreibungen wie Theorie der Gesellschaftsspiele (1928)[1] bzw. theory of games (1944).[2] Obwohl bereits in den Publikationen von 1928 und 1944 ökonomische Anwendungen als primäre Zielsetzung formuliert wurden, befinden sich dort mehrfache Hinweise auf Implikationen für Gesellschaftsspiele wie Schach, das Bluffen beim Poker, Baccara und das Signalisieren beim Bridge.[3][4] Auch späteren Autoren dienten Gesellschaftsspiele als Beispiele, etwa für John Forbes Nash in seiner Dissertation von 1950, in der er im Anschluss an einen Existenzbeweis für das nachfolgend nach ihm benannte Gleichgewicht als einfaches Beispiel eine Berechnung für ein Drei-Personen-Poker durchführte.[5] In späterer Zeit wurde im deutschen Sprachraum wiederholt der Begriff Interaktive Entscheidungstheorie für treffender als Spieltheorie befunden. Aufgrund der weiten Verbreitung des Begriffs Spieltheorie konnten sich solche Vorschläge aber nicht durchsetzen.[6]
Der Begriff Spieltheorie taucht wiederum auch in anderen Gebieten der theoretischen Behandlung von Spielen auf – siehe Spielwissenschaft, Spielpädagogik, Ludologie oder Homo ludens.
Anwendung
Die Spieltheorie ist weniger eine zusammenhängende Theorie als mehr ein Satz von Analyseinstrumenten. Anwendungen findet die Spieltheorie vor allem im Operations Research, in den Wirtschaftswissenschaften (sowohl Volkswirtschaftslehre als auch Betriebswirtschaftslehre), in der Ökonomischen Analyse des Rechts (law and economics) als Teilbereich der Rechtswissenschaften, in der Politikwissenschaft, in der Soziologie, in der Psychologie, in der Informatik, in der linguistischen Textanalyse[7] und seit den 1980ern auch in der Biologie (insb. die evolutionäre Spieltheorie).
Kooperative vs. nicht-kooperative Spieltheorie
.jpg.webp)
Generell wird die nicht-kooperative von der kooperativen Spieltheorie so unterschieden: Können die Spieler bindende Verträge abschließen, so spricht man von kooperativer Spieltheorie. Sind hingegen alle Verhaltensweisen (also auch eine mögliche Kooperation zwischen Spielern) self-enforcing, d. h., sie ergeben sich aus dem Eigeninteresse der Spieler, ohne dass bindende Verträge abgeschlossen werden können, so spricht man von nicht-kooperativer Spieltheorie.
Kooperative Spieltheorie ist als axiomatische Theorie von Koalitionsfunktionen (charakteristischen Funktionen) aufzufassen und ist auszahlungsorientiert. Nicht-kooperative Spieltheorie ist dagegen aktions- bzw. strategieorientiert. Die nicht-kooperative Spieltheorie ist ein Teilgebiet der Mikroökonomik, während die kooperative Spieltheorie einen Theoriezweig eigener Art darstellt. Bekannte Konzepte der kooperativen Spieltheorie sind der Kern, die Shapley-Lösung und die Nash-Verhandlungslösung.
Die nicht-kooperative Spieltheorie spielt in der universitären Lehre eine größere Rolle als die kooperative Spieltheorie. Es gibt viele Lehrbücher zur Spieltheorie und es gibt an Universitäten viele Veranstaltungen mit dem Titel Spieltheorie, in denen die kooperative Spieltheorie gar nicht oder nur am Rande behandelt wird. Obwohl die Nobelpreisträger Robert J. Aumann und John Forbes Nash Jr. beide entscheidende Beiträge zur kooperativen Spieltheorie geleistet haben, wurde der Preis vom Nobelpreiskomitee ausdrücklich für ihre Beiträge zur nicht-kooperativen Spieltheorie vergeben.
Dennoch wird in der aktuellen Forschung weiterhin die kooperative Spieltheorie untersucht, und ein Großteil neuer spieltheoretischer wissenschaftlicher Artikel sind der kooperativen Spieltheorie zuzuordnen. Die weiterhin große Bedeutung der kooperativen Spieltheorie in der Forschung ist auch daran abzulesen, dass in der wissenschaftlichen Diskussion sehr präsente Forschungsfelder wie die Verhandlungstheorie und die Matchingtheorie zu einem großen Teil mit den Mitteln der kooperativen Spieltheorie analysiert werden.
Geschichte


Ausgangspunkt
Historischer Ausgangspunkt der Spieltheorie ist die Analyse des Homo oeconomicus, insbesondere durch Daniel Bernoulli, Joseph Bertrand, Antoine-Augustin Cournot (1838), Francis Ysidro Edgeworth (1881), Frederik Ludvig Bang von Zeuthen und Heinrich Freiherr von Stackelberg. Diese spieltheoretischen Analysen waren jedoch immer Antworten auf spezifische Fragestellungen, ohne dass eine allgemeinere Theorie zur Analyse strategischer Interaktion daraus entwickelt worden wäre. Die ersten allgemeinen Überlegungen stellte Émile Borel 1921 an.[8][9]
Grundlagen
Erst die formalisierte Analyse von Gesellschaftsspielen und der Beweis des Min-Max-Theorems durch John von Neumann im Jahr 1928 legte die Grundlage der modernen Spieltheorie.[1] Schnell erkannte John von Neumann die Anwendbarkeit des von ihm entwickelten Ansatzes zur Analyse wirtschaftlicher Fragestellungen, so dass 1944 im Buch „Spieltheorie und wirtschaftliches Verhalten“ (Theory of Games and Economic Behavior), das er zusammen mit Oskar Morgenstern verfasste, bereits eine Verquickung zwischen der mathematischen Theorie und der wirtschaftswissenschaftlichen Anwendung erfolgte. Dieses Buch gilt auch heute noch als wegweisender Meilenstein. Zunächst hatte man nur für Konstantsummenspiele eine Lösung.
Eine allgemeine Lösungsmöglichkeit bot erst das Nashgleichgewicht ab 1950. Danach hat sich die Spieltheorie erst allmählich als anerkannte Methodik in den Wirtschaftswissenschaften sowie mehr und mehr auch in den sozialwissenschaftlichen Nachbardisziplinen durchgesetzt.
Weitere Entwicklung
Seit 1970 ist eine sehr stürmische Entwicklung der Spieltheorie und ein Ausufern in andere Disziplinen zu beobachten. In diesem Sinne entstanden seit damals die Kombinatorische und die Algorithmische Spieltheorie als sehr mathematisch orientierte Zweige sowie die Evolutionäre Spieltheorie, die am stärksten von der Annahme bewusster Entscheidungen abrückt.
Würdigung
Für spieltheoretische Arbeiten wurde bisher acht Mal der Wirtschaftsnobelpreis vergeben, welche die große Bedeutung der Spieltheorie für die moderne Wirtschaftstheorie verdeutlichen: 1994 an John Forbes Nash Jr., John Harsanyi und Reinhard Selten, 1996 an William Vickrey, 2005 an Robert Aumann und Thomas Schelling und 2012 an Alvin Roth und Lloyd S. Shapley. Für ihre Erforschung begrenzter Rationalität erhielten Herbert A. Simon 1978 und Daniel Kahneman 2002 den Nobelpreis. Auch die Preise an Leonid Hurwicz, Eric S. Maskin und Roger B. Myerson im Jahr 2007 für ihre Forschung auf dem Gebiet der Mechanismus-Design-Theorie stehen in engem Zusammenhang zu spieltheoretischen Fragestellungen.
Methodik
Interaktion als Spiel modellieren
Die Spieltheorie modelliert die verschiedensten Situationen als ein Spiel. Dabei ist der Begriff „Spiel“ durchaus wörtlich zu nehmen: In der mathematisch-formalen Beschreibung wird festgelegt, welche Spieler es gibt, welchen sequenziellen Ablauf das Spiel hat und welche Handlungsoptionen (Züge) jedem Spieler in den einzelnen Stufen der Sequenz zur Verfügung stehen.
Beispiele: Im Spiel Cournot-Duopol sind die Spieler die Firmen und ihre jeweilige Handlungsoption ist ihre Angebotsmenge. Im Bertrand-Duopol sind die Spieler wieder die Duopolisten, ihre Handlungsoptionen sind aber hier die Angebotspreise. Im Spiel Gefangenendilemma sind die Spieler die beiden Gefangenen und ihre Aktionsmengen sind aussagen und schweigen. In Anwendungen der Politikwissenschaft sind die Spieler oft Parteien oder Lobbyverbände, während in der Biologie die Spieler meistens Gene oder Spezies sind.
Zur Beschreibung eines Spiels gehört zudem eine Auszahlungsfunktion: Diese Funktion ordnet jedem möglichen Spielausgang einen Auszahlungsvektor zu, d. h., durch diesen Vektor wird festgelegt, welchen Gewinn ein Spieler macht, wenn ein bestimmter Spielausgang eintritt. Bei Anwendungen in den Wirtschaftswissenschaften ist die Auszahlung meistens als monetäre Größe zu verstehen, bei politikwissenschaftlichen Anwendungen kann es sich hingegen um Wählerstimmen handeln, während bei biologischen Anwendungen meistens die Auszahlung aus Reproduktionsfähigkeit oder Überlebensfähigkeit besteht.
Man kann in der Spieltheorie zwei bedeutende Aspekte erkennen:
- Formalisierung
- Ein bedeutender Schritt ist, ein Spiel im Sinne der Spieltheorie zu formalisieren. Die Spieltheorie hat hierfür eine reichhaltige Sprache entwickelt. Siehe unter: Spieldarstellung
- Lösung
- Abhängig vom Kontext kann man in einem weiteren Schritt eine Vorhersage des Spielausganges versuchen. Siehe hierfür: Lösungskonzepte.
Eine wichtige Technik beim Finden von Gleichgewichten in der Spieltheorie ist das Betrachten von Fixpunkten.
In der Informatik versucht man, mit Hilfe von Suchstrategien und Heuristiken (allgemein: Techniken der Kombinatorischen Optimierung und Künstlichen Intelligenz) bestimmte Spiele, wie Schach, SameGame, Mancala, Go zu lösen oder z. B. zu beweisen, dass derjenige, der anfängt, bei richtiger Strategie immer gewinnt (das ist z. B. der Fall für Vier gewinnt, Qubic und Fünf in eine Reihe) oder z. B. derjenige, der den zweiten Zug hat, immer wenigstens ein Unentschieden erzielen kann (Beispiel Mühle). Man spricht in diesem Zusammenhang vom first movers advantage bzw. second movers advantage.
Informationsbegriff
Entscheidend für Darstellung und Lösung ist der Informationsstand der Spieler. Unterschieden werden hierbei drei Begriffe: Vollständige, perfekte (bzw. vollkommene) Information und perfektes Erinnerungsvermögen, je nachdem, ob der Spieler über die Spielregeln, die Züge der anderen Spieler und die eigenen Informationen aus der Vergangenheit informiert ist. Standard ist das Spiel mit vollständiger Information sowie perfektem Erinnerungsvermögen. Perfekte Information gehört nicht zu den Standardannahmen, da sie hinderlich bei der Erklärung zahlreicher einfacher Konflikte wäre.
Vollständige Information, die Kenntnis aller Spieler über die Spielregeln, ist eine Annahme, die man beim Spiel im klassischen Wortsinn (vgl. Spiel) gemeinhin als Voraussetzung für gemeinsames Spielen betrachten wird. Unstimmigkeiten über die Spielregeln, etwa, ob bei Mensch ärgere Dich nicht die Pflicht besteht, einen gegnerischen Kegel zu schlagen, wenn dies im betreffenden Zug möglich ist, oder ob bei Mau Mau eine gezogene Karte sofort gelegt werden darf, wenn sie passt, werden in der Regel als ernsthafte Störung betrachtet, wenn sie nicht vor dem Spiel geklärt wurden. Andererseits wird die Spieltheorie auf viele Situationen angewendet, für die dieses Informationserfordernis zu rigide wäre, da mit dem Vorhandensein gewisser Informationen nicht gerechnet werden kann (z. B. bei politischen Entscheidungen). Darum ist es sinnvoll, die klassische Spieltheorie, die mit vollständiger Information arbeitet, um die Möglichkeit unvollständiger Information zu erweitern. Andererseits ist dieses Feld dadurch begrenzt, weil sich für jedes Spiel mit unvollständiger Information ein Spiel mit vollständiger Information konstruieren lässt, das strategisch äquivalent ist.
Perfekte Information, also die Kenntnis sämtlicher Spieler über sämtliche Züge sämtlicher Spieler, ist eine rigorose Forderung, die in vielen klassischen Spielen nicht erfüllt ist: Sie ist beispielsweise in den meisten Kartenspielen verletzt, weil zu Spielbeginn der Zug des Zufallsspielers und die Verteilung der Blätter unbekannt ist, da man jeweils nur die eigenen Karten einsehen kann. Darum wird in spieltheoretischen Modellen meist nicht von perfekter Information ausgegangen. Erfüllt ein Spiel das Kriterium perfekter Information, ist es in der Regel vom Prinzip her einfacher zu lösen; auch wenn sich in der Realität wie beim Schach aufgrund der Komplexität große Hürden ergeben.
Perfektes Erinnerungsvermögen ist das Wissen jedes Spielers über sämtliche Informationen, die ihm bereits in der Vergangenheit zugänglich waren. Obwohl diese Annahme zumindest vom Prinzip her auf den ersten Blick immer erfüllt zu sein scheint, gibt es Gegenbeispiele: Handelt es sich bei einem Spiel um ein Team kooperierender Akteure wie beim Skat, kennt „der“ einzelne Spieler zum Zeitpunkt einer eigenen Entscheidung nicht mehr den Informationskontext vergangener Züge, die ein Partner aufgrund seiner Karten getroffen hat.
Darstellungsformen
Spiele werden meist entweder in strategischer (Normal-)Form oder in extensiver Form beschrieben. Weiterhin ist noch die Agentennormalform zu nennen. Da es Spiele gibt, denen keine dieser Formen gerecht wird, muss bisweilen auf allgemeinere mathematische oder sprachliche Beschreibungen zurückgegriffen werden.
Die Extensivform
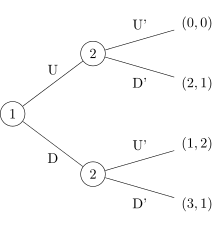
Die Extensivform eines Spiels bezeichnet in der Spieltheorie eine Darstellungsform von Spielen, die sich auf die Baumdarstellung zur Veranschaulichung der zeitlichen Abfolge von Entscheidungen stützt.
Die Normalform
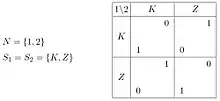
Die Normalform eines Spiels beschränkt sich im Wesentlichen auf die A-priori-Strategiemengen der einzelnen Spieler und eine Auszahlungsfunktion als Funktion der gewählten Strategiekombinationen. Gerecht wird diese Darstellungsform am ehesten solchen Spielen, bei denen alle Spieler ihre Strategien zeitgleich und ohne Kenntnis der Wahl der anderen Spieler festlegen. Zur Veranschaulichung verwendet man meist eine Bimatrixform.
Die Agentennormalform
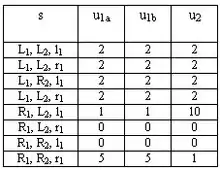
Wer oder was ist eigentlich ein Spieler in einer gegebenen Situation? Die Agentennormalform beantwortet diese Frage so: Jeder Zug im Verlauf eines Spiels verlangt nach einem Spieler im Sinne eines unabhängigen Entscheiders, da die lokale Interessenlage einer Person oder Institution von Informationsbezirk zu Informationsbezirk divergieren kann. Dazu verfügt die Agentennormalform generell über so viele Spieler bzw. Agenten, wie es Informationsbezirke persönlicher Spieler gibt. Der „natürliche“ Spieler 1 wird hier beispielsweise zu den Agenten 1a und 1b abstrahiert.
Lösungskonzepte
Sobald ein Spiel definiert ist, kann man sodann das Analyseinstrumentarium der Spieltheorie anwenden, um beispielsweise zu ermitteln, welche die optimalen Strategien für alle Spieler sind und welches Ergebnis das Spiel haben wird, falls diese Strategien zur Anwendung kommen.
Um Fragestellungen spieltheoretisch zu analysieren, werden sogenannte Lösungskonzepte verwendet.
Gleichgewichte
Das weitaus prominenteste Lösungskonzept, das Nash-Gleichgewicht, stammt von John Forbes Nash Jr. (1950). Die obige Fragestellung – welche möglichen Ausgänge ein Spiel hat, wenn sich alle Spieler individuell optimal verhalten – kann durch die Ermittlung der Nash-Gleichgewichte eines Spiels beantwortet werden: Die Menge der Nash-Gleichgewichte eines Spiels enthält per Definition diejenigen Strategieprofile, in denen sich ein einzelner Spieler durch Austausch seiner Strategie durch eine andere Strategie bei gegebenen Strategien der anderen Spieler nicht verbessern könnte.
Weitere Gleichgewichte
Für andere Fragestellungen gibt es andere Lösungskonzepte. Wichtige sind das Minimax-Gleichgewicht, das wiederholte Streichen dominierter Strategien sowie Teilspielperfektheit und in der kooperativen Spieltheorie der Core, der Nucleolus, die Verhandlungsmenge und die Imputationsmenge.
Gemischte vs. reine Strategien
Während die reine Strategie eines Spielers eine Funktion ist, die jeder Spielstufe, in der die Aktionsmenge des Spielers nicht leer ist, eine Aktion zuordnet, ist eine gemischte Strategie eine Funktion, die jeder Spielstufe, in der die Aktionsmenge des Spielers nicht leer ist, eine Wahrscheinlichkeitsverteilung über der in dieser Spielstufe verfügbaren Aktionsmenge zuordnet. Damit ist eine reine Strategie der Spezialfall einer gemischten Strategie, in der immer dann, wenn die Aktionsmenge eines Spielers nicht leer ist, die gesamte Wahrscheinlichkeitsmasse auf eine einzige Aktion der Aktionsmenge gelegt wird. Man kann leicht zeigen, dass jedes Spiel, dessen Aktionsmengen endlich sind, ein Nash-Gleichgewicht in gemischten Strategien haben muss. In reinen Strategien ist die Existenz eines Nash-Gleichgewichtes hingegen für viele Spiele nicht gewährleistet. Die Analyse von Gleichgewichten in gemischten Strategien wurde wesentlich durch eine Reihe von Beiträgen John Harsanyis in den 70er und 80er Jahren vorangebracht.
Einige besondere Probleme
Im Folgenden sollen auf der Basis der beschriebenen Spielformen und deren Lösungskonzepte einige Probleme genannt werden, die sich in der spieltheoretischen Behandlung als besonders einflussreich erwiesen haben.
Einmalige vs. wiederholte Spiele
Ein Spiel, das nach einmaliger Durchführung nicht wiederholt wird, wird als sogenanntes One-Shot-Game bezeichnet. Wird ein One-Shot-Game mehrmals hintereinander durchgeführt, wobei sich im Allgemeinen die Gesamtauszahlung für jeden Spieler durch die (eventuell aufdiskontierten) Auszahlungen jedes einzelnen One-Shot-Games ergibt, so spricht man von einem wiederholten Spiel. Die gesamte Folge aller One-Shot-Games bezeichnet man als Superspiel. In der Spieltheorie unterscheidet man zudem zwischen endlich wiederholten und unendlich wiederholten Superspielen.
Die Analyse wiederholter Spiele wurde wesentlich von Robert J. Aumann vorangebracht.
Ein Lösungskonzept vieler endlich wiederholter Spiele ist die sogenannte Rückwärtsinduktion, indem zunächst die Lösung des letzten One-Shot-Games ermittelt und darauf basierend die Lösungen der vorangegangenen Spiele bis zum ersten Spiel bestimmt werden. Eine bekannte Anwendung der Backward-Induction ist das sogenannte Chainstore-Paradoxon.
Unvollständige Information und Reputation
Kennt ein Spieler selbst nur seinen eigenen Typ, während andere nur diesbezügliche probabilistische Erwartungen hegen, so spricht man von unvollständiger, speziell asymmetrischer Information. Reputationseffekte treten immer dann auf, wenn ein Spieler für andere als einem bestimmten Typ zugehörig identifiziert werden kann.
Allgemein bekannte Spielregeln
Die Spieltheorie unterstellt zunächst nicht nur jedem Spieler Rationalität, sondern auch, dass alle Spieler wissen, dass alle Spieler rational sind etc. Man unterstellt also allgemein bekannte Spielregeln, bzw. allgemein bekannte Rationalität. Im Unterschied zur „perfekten“ Rationalität werden zunehmend auch Spieltheorien mit eingeschränkter Rationalität formuliert, die ggf. auch Zweifel an der Rationalität von Spielern zulassen (u. a. auch in der evolutionären Spieltheorie).
Evolutionäre Spieltheorie
Von evolutionärer Spieltheorie spricht man meist dann, wenn das Verhalten der Spieler nicht durch rationale Entscheidungskalküle abgeleitet wird, sondern als Ergebnis von kulturellen oder genetischen Evolutionsprozessen begründet wird. Oft kann man die stabilen Ergebnisse durch statische Stabilitätskonzepte charakterisieren. Ein derartiges Konzept ist die evolutionär stabile Strategie, auch kurz „ESS“ genannt (Maynard Smith und Price, 1973). Evolutionstheoretisch besagt diese Spieltheorie, dass jeweils nur die am besten angepasste Strategie bzw. Mutante überleben kann.
Spieltheorie und Mechanismus-Design
Die Spieltheorie untersucht, wie rationale Spieler ein gegebenes Spiel spielen. In der Mechanismus-Designtheorie wird diese Fragestellung jedoch umgekehrt, und es wird versucht, zu einem gewollten Ergebnis ein entsprechendes Spiel zu entwerfen, um den Ausgang bestimmter regelbezogener Prozesse zu bestimmen oder festzulegen. Dies geschieht im Zuge der Lösungen für ein Mechanismus-Design-Problem. Dieses Vorgehen kann nicht nur für "reine" Spiele, sondern auch für das Verhalten von Gruppen in Wirtschaft und Gesellschaft genutzt werden.
Rezeption
Die Spieltheorie erlaubt es, soziale Konfliktsituationen, die strategische Spiele genannt werden, facettenreich abzubilden und mathematisch streng zu lösen. Aufgrund der unrealistischen Modellannahmen wird die empirische Erklärungskraft der Spieltheorie in der Regel in Abrede gestellt. Kein Mensch wird jemals so rational sein, wie es den Spielern durch die spieltheoretischen Lösungskonzepte unterstellt wird. Menschen unterliegen stets kognitiven Beschränkungen, die perfekt rationales Verhalten in komplexen Spielen ausschließen. Indes muss nach Auffassung des Bamberger Politikwissenschaftlers Reinhard Zintl zwischen dem Anwendungsfall als Verhaltenstheorie und demjenigen als Verfassungstheorie unterschieden werden; und es sei je nach Erklärungsproblem auch eine inkonsistente Verwendung einzelner Akteursmodelle durchaus gestattet und zweckmäßig.[10]
Beispiele
Berühmte Probleme
Siehe auch
Literatur
- Christian Rieck: Spieltheorie – eine Einführung. Rieck, Eschborn 2012, ISBN 978-3-924043-91-9.
- Florian Bartholomae, Marcus Wiens: Spieltheorie - Ein anwendungsorientiertes Lehrbuch. Springer Gabler Verlag, Wiesbaden 2016, ISBN 978-3-8349-4419-1.
- Michael Sauer: Operations Research kompakt. Oldenbourg Verlag, München 2009, ISBN 978-3-486-59082-1.
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. 5. Auflage. Vieweg+Teubner Verlag, Wiesbaden 2010, ISBN 3-8348-0775-3, doi:10.1007/978-3-8348-9696-4 (behandelt Anwendungen auf Gesellschaftsspiele und die historische Entwicklung).
- Andreas Diekmann: Spieltheorie: Einführung, Beispiele, Experimente. Rowohlts Enzyklopädie, Reinbek bei Hamburg 2009, ISBN 978-3-499-55701-9.
- Steven N. Durlauf, Lawrence E. Blume: Game Theory. Palgrave Macmillan, 2010, ISBN 978-0-230-23890-9.
- Manfred Eigen, Ruthild Winkler: Das Spiel. Piper, München 1987, ISBN 3-492-02151-4 (Spieltheorie im naturwissenschaftlichen Umfeld, neu aufgelegt 2010: ISBN 978-3-924043-95-7).
- Len Fisher: Schere, Stein, Papier. Spieltheorie im Alltag. aus dem Englischen von Andreas Held. Spektrum Akademischer Verlag, Heidelberg 2010, ISBN 978-3-8274-2467-9.
- Drew Fudenberg, Jean Tirole: Game Theory. MIT Press, Cambridge/MA 1991, ISBN 978-0-262-06141-4.
- Robert Gibbons: A prime in game theory. Harvester Wheatsheaf, New York 1992, ISBN 0-7450-1159-4.
- Herbert Gintis: Game theory evolving. 2. Aufl. Princeton University Press, Princeton 2009, ISBN 978-0-691-14050-6.
- Manfred J. Holler, Gerhard Illing: Einführung in die Spieltheorie. 6. Auflage. Springer Verlag, Berlin 2005, ISBN 3-540-27880-X.
- Alexander Mehlmann: Strategische Spiele für Einsteiger – Eine verspielt-formale Einführung in Methoden, Modelle und Anwendungen der Spieltheorie. (Reihe: Mathematik für Einsteiger). Vieweg + Teubner, 2007, ISBN 978-3-8348-0174-6.
- Roger B. Myerson: Game Theory. Analysis of Conflict. Harvard University Press 1991, ISBN 0-674-34115-5.
- John von Neumann, Oskar Morgenstern: Theory of Games and Economic Behavior. University Press, Princeton NJ 2004, ISBN 0-691-11993-7 (Erstveröffentlichung 1944, gilt als erste systematische Veröffentlichung zur Spieltheorie).
- Wolfgang Ortmanns: Entscheidungs- und Spieltheorie: eine anwendungsbezogene Einführung. Verlag Wissenschaft & Praxis, Sternenfels 2008, ISBN 978-3-89673-489-1.
- Martin J. Osborne, Ariel Rubinstein: Bargaining and Markets. Academic Press, San Diego 1990, ISBN 0-12-528631-7.
- Martin J. Osborne, Ariel Rubinstein: A Course in Game Theory. MIT Press, 1994, ISBN 0-262-65040-1.
- Guillermo Owen: Game Theory. Academic Press, San Diego 1995, ISBN 0-12-531151-6.
- Burkhard Rauhut, Norbert Schmitz und Ernst-Wilhelm Zachow: Spieltheorie. Teubner, Stuttgart 1979.
- Anna Karlin, Yuval Peres: Game theory, Alive, American Mathematical Society 2017, pdf
- Michael Maschler, Eilon Solan, Shmuel Zamir: Game Theory, Cambridge University Press 2013
Weblinks
- Don Ross: Game Theory. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Till Grüne-Yanoff: Game Theory. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
- Vorlesungsskript Einführung in die Spieltheorie von Prof. Dr. Leininger (TU Dortmund)
- Open Yale Courses: ECON 159: Game Theory – Vorlesungen zum Download (24 × 75 Minuten) von der Yale University
- Games and AI Group des Fachbereichs Informatik der Universität Maastricht (englisch) – Computergestützte Strategien in Gesellschaftsspielen
- Gametheory.net (englisch)
- Wikiludia
- Gambit – Software zur Analyse von endlichen, strategischen und extensiven Spielen
- Professor Rieck's Spieltheorie-Seite – Einfache Beispiele und Erklärungen zur Spieltheorie
Einzelnachweise
- John von Neumann: Zur Theorie der Gesellschaftsspiele, Mathematische Annalen, Band 100, 1928, S. 295–320, doi:10.1007/BF01448847, online (frei zugänglich).
- John von Neumann, Oskar Morgenstern: Theory of games and economic behavior, Princeton 1944.
- Axel Ockenfels: Stichwort Spieltheorie im Gabler Wirtschaftslexikon, abgerufen am 30. April 2018.
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, Springer Spektrum, 6. Auflage, Wiesbaden 2012, ISBN 978-3-8348-1923-9, doi:10.1007/978-3-8348-2319-9, S. 246 ff.
- John Nash: Non-cooperative games, 1950, Online-Version (Memento vom 17. September 2012 im Internet Archive)
- Bastian Fromen: Faire Aufteilung in Unternehmensnetzwerken: Lösungsvorschläge auf der Basis der kooperativen Spieltheorie, Springer, Wiesbaden 2013, ISBN 978-3-8244-8164-4, doi:10.1007/978-3-322-81803-4, S. 55 in der Google-Buchsuche
- Vgl. Reinhard Breymayer: Zur Pragmatik des Bildes. Semiotische Beobachtungen zum Streitgespräch Mk 12, 13–17 („Der Zinsgroschen“) unter Berücksichtigung der Spieltheorie. In: Linguistica Biblica. Interdisziplinäre Zeitschrift für Theologie und Linguistik 13/14 (1972), S. 19–51.
- Émile Borel: La théorie du jeu et les équations intégrales à noyau symétrique gauche In: Comptes rendus hebdomadaires des séances de l’Académie des sciences. 173, 1921, S. 1304–1308 (gallica.bnf.fr).
- Maurice Fréchet: Commentary on the Three Notes of Emile Borel. In: Econometrica. Band 21, Heft 1 (Jan. 1953), S. 118–124, JSTOR 1906949
- Reinhard Zintl: Der Nutzen unvollständiger Erklärungen: Überlegungen zur sozialwissenschaftlichen Anwendung der Spieltheorie. Vortrag gehalten am 13. Februar 1995 im Max-Planck-Institut für Gesellschaftsforschung in Köln (hier (PDF; 32 kB) in elektronischer Fassung lesbar).