Rechenmaschine
Eine Rechenmaschine, veraltet auch Kalkulator, ist eine Maschine, mit deren Hilfe mathematische Berechnungen automatisiert ausgeführt werden können. Eine Rechenmaschine ist also ein Rechenhilfsmittel, das die Berechnung aufwendigerer mathematischer Aufgaben unterstützt, indem dem Benutzer der Maschine möglichst wenig kognitiver Aufwand abverlangt wird. Welche Berechnungen möglich sind, hängt von der Maschine selbst und von den für diese Maschine angebotenen Algorithmen ab.



Die ersten Rechenmaschinen waren mechanisch per Hand angetrieben. Bis in die 1970er Jahre weit verbreitet waren vor allem die verhältnismäßig preiswerten Addiermaschinen. Sie beherrschten lediglich Addition und Subtraktion, weshalb sie auch Zwei-Spezies-Maschinen genannt wurden. Teure Drei-Spezies-Maschinen konnten zusätzlich die Multiplikation und Vier-Spezies-Maschinen auch die Division mehr oder weniger automatisch laut und langsam ausführen. Vereinzelt gab es auch elektromechanische Rechenmaschinen, die zusätzlich die Quadratwurzel ziehen konnten.
Drei- und Vierspeziesmaschinen wurden vor allem nach zwei Prinzipien konstruiert: Staffelwalze und Sprossenrad.
Historische Entwicklung
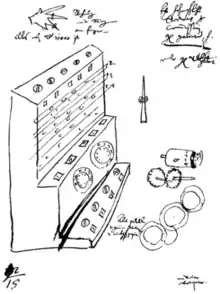
Die erste urkundlich erwähnte Rechenmaschine wurde 1623 von Wilhelm Schickard in einem Brief an Johannes Kepler knapp beschrieben.[1] Die Maschine habe aus einem Addier- und Subtrahierwerk sowie einer Vorrichtung zum Multiplizieren und Dividieren nach Art der Napierschen Rechenstäbchen bestanden. Schickard berichtete, er habe diese Maschine auch realisiert. Man vermutet, dass diese Maschine später während eines Brandes seines Hauses verloren gegangen ist. Sie wurde 1960 rekonstruiert.
1645 führte der Franzose Blaise Pascal seine Rechenmaschine „Pascaline“ vor, die mit Zahnrädern und Sperrklinken funktioniert. Pascal fertigte einige dieser Maschinen und versandte sie an europäische Fürstenhäuser. Aus diesem Grund existieren heute neben vielen Nachbauten auch noch einige Original-Pascalinen.[2]
Zwischen deutschen und französischen Historikern besteht Uneinigkeit, welche Nation die erste Rechenmaschine hervorgebracht hat. Diese Frage ist nicht eindeutig zu beantworten. Von Schickard ist die erste Konstruktionszeichnung und von Pascal die erste erhaltene Maschine nachweisbar.
Beide Maschinentypen haben ein gemeinsames Problem. Sie eignen sich nicht für den alltäglichen Einsatz als Rechenmaschinen. Sie enthalten wichtige Funktionsprinzipien, nicht aber Vorrichtungen, die das tägliche sichere Arbeiten ermöglichen.
So fehlt der Maschine von Wilhelm Schickard die Möglichkeit, Energie für den Zehnerübertrag jeder Dezimalstelle zu speichern. Das bedeutet, dass die Rechnung 9+1 einfach zu bewältigen ist, jedoch 9999+1 hohen Kraftaufwand erfordert und vermutlich zu Verklemmungen der Maschine geführt hat.
In der Maschine von Blaise Pascal verhindern Sperrklinken eine freie Drehbarkeit der Zahnräder, diese werden durch Schwerkraft unten gehalten. Dies führt dazu, dass die Maschine unter dem Phänomen des „Überschleuderns“ leidet. Das Problem dabei ist, dass sich Zahnräder oder ganze Getriebe als träge Masse auch ohne Antrieb weiterbewegen mit dem Resultat, dass das Rechenergebnis verfälscht wird, da die Maschine bei Addition 1 oder mehr zu viel zählt.
.jpg.webp)

1673 stellte Gottfried Wilhelm Leibniz eine von ihm entwickelte Staffelwalzen-Maschine der Royal Society in London vor.
Zitat von Leibniz:
„Es ist unwürdig, die Zeit von hervorragenden Leuten mit knechtischen Rechenarbeiten zu verschwenden, weil bei Einsatz einer Maschine auch der Einfältigste die Ergebnisse sicher hinschreiben kann.“
Wie gut diese Maschine tatsächlich funktionierte, kann nicht mit letzter Sicherheit gesagt werden. Zum Ende des 19. Jahrhunderts wurde der deutsche Rechenmaschinenfabrikant Arthur Burkhardt beauftragt, die Leibniz-Maschine zu reparieren.[3] Nikolaus Joachim Lehmann hat bei Untersuchungen der originalen Leibniz-Rechenmaschine (entstanden etwa 1700–1716) einen prinzipiellen Denkfehler bei Restaurierungsarbeiten um 1894 festgestellt, der eine vollständige Funktionsfähigkeit des Übertragungsmechanismus verhinderte. Es erfolgte ein voll funktionsfähiger Nachbau des Gerätes in Originalabmessungen, der Leibniz' Intentionen voll entspricht, an der TU Dresden.[4] In Hannover stellten Erwin Stein und Franz Otto Kopp Untersuchungen zur Leibnizschen Rechenmaschine an und fertigten einen Nachbau an.
Die damalige Fertigungstechnik konnte zwar Zahnräder und andere mechanische Teile sehr genau fertigen, war jedoch von einem Austauschbau weit entfernt. Die einzelnen Teile mussten manuell gefertigt und durch Nacharbeit aneinander angepasst werden. Auch wenn die Konstruktion der Mechanik für die 10er-Stelle identisch zur 100er-Stelle war, konnte man die beweglichen Teile nicht zwischen beiden Stellen tauschen, ohne nacharbeiten zu müssen.
Deshalb ist davon auszugehen, dass die Originalmaschine von Leibniz die Beispielaufgaben ordnungsgemäß rechnen konnte, doch im Laufe der Zeit durch Umbauten und Fehlreparaturen blockiert wurde. Die Nachbauten des Heinz Nixdorf MuseumsForum und des Deutschen Museums funktionieren jedenfalls tadellos. Sie sind jedoch auch unter Verwendung moderner Fertigungstechniken entstanden.
Leibniz fertigte eine Rechenmaschine mit allen notwendigen Konstruktionsmerkmalen. Zu einer Serienfertigung kam es nie.
1709 veröffentlichte der italienische Mathematiker und Astronom Giovanni Poleni (1683–1761) die Konstruktionszeichnungen seiner hölzernen Rechenmaschine. Diese funktionierte auf Basis von Zahnrädern mit veränderbarer Zähneanzahl, den sogenannten Sprossenrädern. Die Realisierung seiner Maschine scheiterte an den damaligen Fertigungsmöglichkeiten, so dass Poleni seine Maschine eigenhändig zerstörte. Nachbauten existieren z. B. im Museo della Scienza e della Tecnologia di Milano (Mailand) und im Arithmeum Bonn.
1727 wurde die von Antonius Braun (1686–1728) konstruierte Sprossenradrechenmaschine für den Wiener Hof fertig. Sie war Kaiser Karl VI. gewidmet und befindet sich heute im Kunsthistorischen Museum Wien. Ein exakter Nachbau dieser Maschine ist im Arithmeum Bonn ausgestellt. Bezüglich der Einsatzfähigkeit der Maschine für den Alltagsbetrieb hat man beim Vermessen und Replizieren festgestellt, dass sie nur über drei bis vier Stellen fehlerlos arbeiten konnte: Der Zehnerübertrag funktionierte nicht über eine größere Anzahl von Stellen. Immerhin erlaubten Konstruktion und feinmechanische Genauigkeit zu dieser Zeit eine solche Entwicklung.
1727 veröffentlichte der deutsche Mechaniker Jacob Leupold (1674–1727) in seiner technischen Enzyklopädie Theatrum Aritmetico Geometricum Konstruktionszeichnungen einer von ihm erfundenen Rechenmaschine, die nach dem Stellsegmentprinzip arbeitete. Man vermutet, dass Braun diese Konstruktion schon vor der Erstveröffentlichung kannte und die Maschine um 1727 nachbaute. Sie wurde aber erst um 1736 von dem französischen Instrumentenbauer Philippe Vayringe (1684–1746) fertiggestellt (Inschrift: „Braun invenit, Vayringe fecit“). Deshalb wird die Rechenmaschine des Antonius Braun heute als Leupold-Braun-Vayringe-Maschine bezeichnet. Sie befindet sich im Deutschen Museum München.
Ab 1770 konstruierte der Pfarrer und Erfinder Philipp Matthäus Hahn (1739–1790) eine Rechenmaschine in Dosenform mit konzentrisch angeordneten Zahnrädern, Staffelwalzen und einer zentralen Antriebskurbel. Von dieser Maschine fertigte er vier oder fünf Exemplare, die zum Teil heute noch existieren (je eine im Württembergischen Landesmuseum in Stuttgart und im Technoseum in Mannheim) und funktionstüchtig sind. Sie ist die erste voll funktionstüchtige Vierspezies-Rechenmaschine mit mehrstelligem Umdrehungszählwerk und zweistufigem Zehnerübertrag. Das Exemplar in Stuttgart rechnet 11-stellig und das in Mannheim 12-stellig. Die von Leupold inspirierte zentrale Antriebskurbel, das Staffelwalzenprinzip und die verbesserten Fertigungsmöglichkeiten trugen dazu bei, dass viele Historiker in der Maschine von Philipp Matthäus Hahn die erste alltagstaugliche Rechenmaschine sehen.
Johann Helfrich von Müller (1746–1830) wurde bekannt, als es ihm zwischen 1782 und 1784 gelang, eine funktionsfähige 3-Spezies-Rechenmaschine herzustellen, welche die vier Grundrechenarten mittels eines 14-stelligen Rechenwerkes ausführen konnte. Die Operanden wurden dabei über manuelle Drehwähler voreingestellt. Es handelte sich um eine Maschine nach dem Staffelwalzen-Prinzip.
Neben der Rechenmaschine von Leibniz sind zwei von Hahn und drei von Johann Christoph Schuster (1759–1823) erhalten (Schuster I, 1789–1792, zwölfstellig und Schuster II, 1805–1820, neunstellig im Deutschen Museum in München und Schuster III, zehnstellig im Arithmeum in Bonn), während die Beireis-Maschine (elfstellig) und die Herrenberger Maschine (14-stellig) heute verschollen sind.[5]

Ab 1810 fertigte der Erfinder Abraham Stern im heutigen Polen eine Reihe von Rechenmaschinen, die die vier Grundrechenarten durchführten und die Quadratwurzel zogen.
1834 erbaute Luigi Torchi die weltweit erste Maschine zur Direktmultiplikation.[6]
Der Mathematiker Chajim Slonimski, Schwiegersohn von Abraham Stern, erfand 1840 eine Rechenmaschine, begründet auf seinem selbst entdeckten mathematischen Theorem, und erhielt dafür als erster jüdischer Wissenschaftler am 26. Mai 1845 den Demidow-Preis der Petersburger Akademie der Wissenschaften.[7]
1844 ließ Jean-Baptiste Schwilgué, Erbauer der derzeitigen astronomischen Uhr des Straßburger Münsters, eine Tastenaddiermaschine patentieren. Es handelt sich um die dritte[8] weltweit erhaltene tastengesteuerte Rechenmaschine. Schwilgué baute auch eine große mechanische Rechenmaschine, deren Berechnungen für die Einstellung der von ihm entwickelten hoch präzisen Zahnradfräsmaschine dienten.
Im 1861 gegründeten Stadtmuseum in Göteborg ist eine (bereits 1878 dort erwähnte) Maschine „von Sauter in Eßlingen [am Neckar]“ – gemeint ist wahrscheinlich Johann Jacob Sauter jun. (geb. 1770 in Onstmettingen) oder vielleicht sein Bruder Johann Ludwig Sauter (geb. 1780) – erhalten. Im Science Museum in London befindet sich eine offenbar von demselben Erbauer hergestellte Addiermaschine, „verfertigt durch J. Sauter in Eßlingen [am Neckar]“.
Obwohl die technischen Fertigungsmöglichkeiten zu dieser Zeit eine begrenzte Produktion dieser Maschinen zugelassen hätten und zumindest die Rechenmaschinen von Hahn brauchbar waren, wurde keine Maschine der oben genannten Erfinder in Serie gebaut. Dies mag darin begründet sein, dass die Rechenmaschinen am Beginn ihrer Entwicklung standen, infolgedessen für die praktische Anwendung noch nicht ausgereift genug und zu teuer in der Herstellung waren. Der wesentlichste Grund war jedoch, dass es noch keinen Markt für solche Maschinen gab. Staatliche Verwaltungen, das Militär oder Kaufleute litten nicht unter Zeitdruck oder Arbeitskräftemangel.
Serienfertigung
1820 erhielt der Franzose Charles Xavier Thomas (1785–1870) ein französisches Privileg (Patent) für seine Rechenmaschinenkonstruktion. Nach weiteren Versuchen begann er um 1850 mit der weltersten Serienproduktion von Rechenmaschinen. Thomas war Direktor zweier Versicherungsgesellschaften und betrieb seine Rechenmaschinenproduktion nur nebenbei. Bis zu seinem Tod 1870 waren seine Rechenmaschinen ein Zuschussgeschäft, der Verkaufspreis lag unter den Selbstkosten. Von 1820 bis 1878 wurden etwa 1500 Geräte gefertigt. Da aus der Anfangszeit nur zwei Rechenmaschinen bekannt sind, ist davon auszugehen, dass der eigentliche Schwerpunkt der Serienfertigung in der zweiten Hälfte des 19. Jahrhunderts liegt. Die Rechenmaschinen trugen den Namen Arithmomètre und funktionierten nach dem Staffelwalzenprinzip mit einem verschiebbaren Schlitten. Sie funktionierten zuverlässig, waren jedoch zu ihrer Zeit Hochtechnologie und konnten nur in Paris gewartet und repariert werden.
Durch die Verfügbarkeit von Rechenmaschinen entwickelte sich langsam auch ein Markt für numerische Berechnungen. So konnten Unternehmen erstmals wöchentlich oder gar täglich bilanzieren, Ingenieure konnten neben dem Rechenschieber auch algebraische Verfahren anwenden.
1876 konstruierte der Schwede Willgodt Theophil Odhner (1845–1905) eine Sprossenradmaschine, deren Bauprinzip der späteren europäischen Sprossenradmaschinenindustrie als Vorbild diente. Die damals erhältlichen Thomas-Maschinen waren seiner Meinung nach zu schwer zu bekommen und außerdem nicht handlich genug. Seine Maschine sollte klein, einfach, leicht zu bedienen und preiswert sein. Seit 1874 befasste er sich mit dem Bau einer mit den existierenden Werkzeugmaschinen zu fertigenden Sprossenradrechenmaschine und stellte wahrscheinlich 1876 die erste Maschine fertig. Am 19. November 1878 erhielt der Geschäftspartner von Odhner, ein gewisser Königsberg, das Deutsche Patent Nr. 7393. Im Jahre 1879 erhielt Odhner das Schwedische Patent Nr. 123 und das Russische Patent Nr. 2329 auf seine Konstruktion. Dabei beanspruchte Odhner das Sprossenrad und dessen Sprossenverstellung mit Hilfe eines Stellrings mit Kurvenschlitz nicht als sein geistiges Eigentum.
Die Produktion der Rechenmaschinen unter dem Namen Arithmometer startete 1886 in Odhners eigener Fabrik in Sankt Petersburg. In dieser Zeit wurden nur wenige Maschinen produziert. Die späteren erfolgreichen Maschinen, die von Odhner und der deutschen Firma Grimme, Natalis & Co produziert wurden, beruhen auf dem deutschen Patent Nr. 64 925 aus dem Jahre 1890. Odhner vergrößerte 1894 seine Fabrik und stellte neben Rechenmaschinen auch noch andere mechanische Geräte her. Im russisch-japanischen Krieg 1904 bis 1905 wurden statt Rechenmaschinen Instrumente für die Marineartillerie hergestellt. Der Firmengründer W. T. Odhner erlebte die Wiederaufnahme der Rechenmaschinenproduktion nicht mehr. Er starb am 15. September 1905 in Sankt Petersburg. Seine Firma siedelte nach der Oktoberrevolution 1918 nach Göteborg in Schweden um.[9] Die russische Produktion belief sich bis zu diesem Jahr auf ca. 30.000 Rechenmaschinen, die größtenteils auf dem russischen Markt abgesetzt wurden.
Um 1900 gab es schon mehrere Firmen, die ausschließlich Rechenmaschinen herstellten. Die Investition von Charles Xavier Thomas, die Landreformen und die sozialen Umbrüche trugen dazu bei, dass sich ein florierender Markt für Rechenmaschinen entwickeln konnte. Die Autarith von Alexander Rechnitzer war 1906 die erste elektrisch angetriebene, vollautomatische Rechenmaschine.
Auch die Carl Walther GmbH stellte zwischen den Jahren 1924 und 1974 Walther-Rechenmaschinen her.[10]
Als Krönung der Entwicklung der mechanischen Rechenmaschinen gilt die Taschenrechenmaschine Curta des österreichischen Ingenieurs Curt Herzstark. Sie wurde von 1947 bis 1970 in Liechtenstein durch die Firma Contina AG in hohen Stückzahlen hergestellt.
Das Ende der mechanischen Rechenmaschinen


Mit der Entdeckung der Elektrizität wurden mechanische durch elektromechanische Rechenmaschinen ergänzt und abgelöst. Das Ersetzen von Handkurbeln und -hebeln durch einen Elektromotor bedeutete besonders bei Drei- und Vierspeziesmaschinen eine erhebliche Zeit- und Kraftersparnis, aber auch noch mehr Lärm. Die weitere Entwicklung zielte auf programmgesteuerte Rechenmaschinen, wie sie zuerst von Konrad Zuse realisiert wurden und darauf als Computer immer bedeutendere Anwendungen fanden.
1952 erschien die ES, der erste deutsche Elektronenrechner auf Röhrenbasis, der auf Lochkarten gespeicherte Daten verarbeiten konnte. Entwickelt wurde der Rechner vom Labor für Impulstechnik (LFI), dem Vorläuferunternehmen der Nixdorf Computer AG.[12] Das LFI war der erste deutsche Hersteller von elektronisch arbeitenden Rechnern. Im Jahre 1962 kam die erste elektronische Tisch-Rechenmaschine auf den Markt, die ANITA von Norman Kitz, gebaut von der Bell Punch Company in London. Sie arbeitete mit Röhren. Gleichzeitig erschien mit dem Tischrechner Conti aus dem Hause LFI der weltweit erste Tischrechner mit eingebautem Drucker. Der erste Transistor-Tischrechner war der EC-130 der US-Firma Friden, Inc. in San Leandro, Kalifornien, erhältlich ab 1963. Der Rechner EC-130 hatte einen Röhren-Bildschirm mit vier Zeilen zu je 13 Ziffern[13] und arbeitete erstmals mit der umgekehrten polnischen Notation, welche später auch von HP benutzt wurde. Ein serieller dynamischer Speicher wurde mittels magnetostriktiver Fortpflanzung von Bits auf einem geeigneten Metalldraht realisiert. Eine elektronische Alternative mit Transistoren wurde konzipiert, gelangte jedoch nicht zur Ausführung.[14] Auch die italienische IME 84[15] wurde ab 1963 gebaut. Erst durch kleine integrierte Schaltkreise (mit vielen Transistoren) wurden Rechner immer leistungsfähiger und kompakter; außerdem verringerte sich durch moderne Halbleiter-Technologien der Stromverbrauch.
Mit dem Intel 4004 IC fand der erste in Serienfertigung hergestellte Mikroprozessor (der eigens hierfür entwickelt wurde) seinen Einsatz in einem Tischrechner des japanischen Herstellers Busicom. Das Modell Busicom 141-PF kam 1971 auf den Markt. Schon ein Jahr zuvor hatte Busicom in seinem Modell Handy LE-120A den vollintegrierten Schaltkreis MK6010 von Mostek eingesetzt. Beide Bauteile wurden von Busicom bei den jeweiligen Herstellern Intel und Mostek speziell für die Entwicklung einer möglichst kompakten Rechenmaschine in Auftrag gegeben.
Die ersten kommerziell vertriebenen elektronischen Rechenmaschinen mit Akkumulatoren waren 1970 der Sharp QT-8B und der Sanyo ICC 82-D[16]. Der Ende 1970 erschienene Sharp EL-8, der meist als erster Taschenrechner gilt, enthielt die gleichen Schaltkreise wie der QT-8B und war noch um einiges kompakter, jedoch immer noch 7 cm dick. Die Entwicklung verlief jedoch so schnell, dass schon 1971 Geräte auf den Markt kamen, die wirklich als Taschenrechner bezeichnet werden können.
Die elektronischen Taschen- und Tischrechner haben bis Ende der 1970er Jahre die mechanischen Maschinen praktisch vollständig verdrängt.
Heute wird der Begriff Rechenmaschine üblicherweise für elektronische Tischrechner verwendet, die oft mit einem kleinen Drucker ausgestattet sind, was eine Kontrolle der Berechnung ermöglicht. Bis etwa 1980 hatten Maschinen dieser Bauart[17] oft gar keine LED-Anzeige, sondern nur ein Druckwerk.
Zu den Rechenmaschinen gehören aber auch die Taschenrechner und im weiteren Sinne auch die frei programmierbaren Computer, die auch für Aufgaben verwendet werden, die nichts mit Rechnen zu tun haben, z. B. die Speicherung von Daten. Heute haben Personal Computer in vielen Bereichen die Aufgaben der klassischen Rechenmaschinen übernommen.
Typen von mechanischen Rechenmaschinen
In der Literatur werden neben den oben erwähnten Rechenmaschinen auch verschiedenste Objekte wie Abakus, Rechenschieber oder Napiersche Rechenstäbe als mechanische Rechenmaschinen bezeichnet. Um die hier erläuterten Rechenmaschinen von diesen Geräten abzugrenzen, muss der Begriff der mechanischen Rechenmaschinen näher definiert werden:
Den hier gemeinten mechanischen Rechenmaschinen ist zumindest ein Einstellwerk, ein Resultatwerk und ein automatischer Zehnerübertrag gemeinsam. Der automatische Zehnerübertrag muss dabei nicht die volle Kapazität der Maschine erfassen und darf nur maschinenintern vorhanden sein. Der Zehnerübertrag darf also nicht nur teilweise automatisch, wie bei dem Rechnen mit Spaltenaddiermaschinen üblich, vorhanden sein.
Die Einschränkung, dass eine mechanische Rechenmaschine mit Zahnrädern arbeiten soll, würde die Multipliziermaschinen des Eduard Selling (1834–1920) ausgrenzen, die nach dem Prinzip der Nürnberger Schere arbeiten.
Der nachfolgende Abschnitt soll einen Überblick über die verschiedenen Typen von mechanischen Rechenmaschinen geben:
Addiermaschinen
.jpg.webp)
Die hier vorgenommene Unterteilung betrifft vor allem Funktionalität und Einsatzgebiet der Rechenmaschinen; dabei wird zwischen Addiermaschinen (auch Additionsmaschinen) und Vierspeziesmaschinen unterschieden. Als Addiermaschine wird hier eine Rechenmaschine bezeichnet, deren Konzeption in erster Linie auf die schnelle Addition von Zahlenkolonnen ausgerichtet worden ist. Dass diese Unterteilung nicht zu einer klaren Abgrenzung von verschiedenen Rechenmaschinen führt, wird bei der Definition des Begriffs Vierspeziesmaschinen deutlich.
In Europa werden Addiermaschinen oft als Zweispeziesmaschinen bezeichnet. Dies wird ihrer Verwendung vor allem in den USA nicht gerecht. Auf Volltastatur-Addiermaschinen, die für jede Eingabestelle eine eigene Tastenspalte mit den Ziffern 1 bis 9 haben, kann durchaus schnell und effizient multipliziert und dividiert werden. Im Wesentlichen ersetzt bei der Multiplikation auf einer Volltastatur-Addiermaschine die Handstellung den Schlitten einer europäischen Vierspeziesmaschine. So kann die Multiplikation zweier Zahlen auf einer Addiermaschine wie dem Comptometer der Felt and Tarrant Manufacturing Company aus Chicago schneller durchgeführt werden als auf einer Brunsviga-Sprossenrad-Rechenmaschine aus Braunschweig. Bei fortgesetzter Rechnung und Division spielt die Sprossenrad-Rechenmaschine dagegen wieder ihre Vorteile aus.
Dieser Umstand mag daran liegen, dass in Europa vor allem Sprossenrad- und Staffelwalzenmaschinen hergestellt werden, während in den USA Volltastatur-Addiermaschinen das Rückgrat der Rechenmaschinenproduktion bilden. Die entsprechenden Vergleichswettbewerbe und Werbeaussagen aus der Hochzeit der mechanischen Rechenmaschinen haben hier eventuell noch eine späte Auswirkung.
Spaltenaddiermaschinen
Spaltenaddiermaschinen sind dazu gedacht, bei einer Addition von mehreren Zahlen jede Spalte einzeln aufzusummieren, wie man es bei dem schriftlichen Addieren gewohnt ist. Auch unter diesen Maschinen gibt es Exemplare, die auch für die Multiplikation geeignet sind. Zum Beispiel die Kuli von Adolf Bordt Mannheim (Lit.: Lenz, K., Rechenmaschinen).
Addiermaschinen mit direkter Übertragung
Bei Addiermaschinen mit direkter Übertragung löst der Druck auf eine Taste unmittelbar den Rechenvorgang aus, weshalb diese Maschinen oft als die schnellsten Addiermaschinen bezeichnet werden. Sie sind meist mit einer Volltastatur ausgestattet.
Die Torpedo-Schnelladdiermaschine der Torpedowerke und die Plus der Bell Punch Ltd. London stellen hier eine Ausnahme dar: Sie besitzen für jede Kolonne die Tasten 1 bis 5, also eine halbe Volltastatur oder eine reduzierte Tastatur.
Addiermaschinen mit Antriebshebel

Auf diesen Maschinen tastet man eine Zahl ein und löst den Rechenvorgang mit einem gesonderten Hebel aus. Das Wort Antriebshebel ist hier im weiteren Sinne zu verstehen, es kann sich auch um eine Taste oder eine Kurbel handeln. Des Weiteren wurden einige Fabrikate mit Motoren ausgerüstet, bei denen der Antriebshebel nur noch auslösende Funktion hatte. Addiermaschinen mit Antriebshebel waren mit der oben erwähnten Volltastatur oder mit einer Zehnertastatur ausgestattet, wie man sie von heutigen Taschenrechnern kennt.
Der Nachteil der Addiermaschinen mit Antriebshebel gegenüber den Maschinen ohne Antriebshebel ist, dass sie pro Zahl einen zusätzlichen Tastendruck benötigen. Dafür ist der Tastenanschlag meist leichter, denn die Energie für den Mechanismus liefert der Antriebshebel. Die Bauweise einer Maschine mit Antriebshebel ist leichter zu beherrschen, insbesondere besitzen sie einen einfacheren Zehnerübertragmechanismus. Ein für Anfänger im Maschinenrechnen interessanter Aspekt ist die Kontrollmöglichkeit der Eingabe und deren unproblematische Korrektur, die auf Maschinen mit direkter Übertragung nicht möglich ist.
Die erwähnten Spaltenaddiermaschinen haben fast ausnahmslos keinen Antriebshebel.
Druckende und schreibende Addiermaschinen
Druckende Addiermaschinen können Rechnung und Ergebnis zu Papier bringen. Mit einer schreibenden Addiermaschine kann man die Rechnung um weiteren Text ergänzen.
Vierspezies-Rechenmaschinen
Die Gattungsbezeichnung Vierspezies-Rechenmaschine soll im Allgemeinen eine Rechenmaschine sein, auf der man zumindest alle vier Grundrechenarten rechnen kann. Näheres ist im Artikel über Vier-Spezies-Maschinen nachzulesen.
Die nachfolgend aufgeführten Funktionsprinzipien wurden vorwiegend für Vierspezies-Maschinen verwendet:
Staffelwalzenmaschinen
Siehe den Artikel Staffelwalze
Sprossenradmaschinen
Siehe den Artikel Sprossenrad
Proportionalhebel- und Schaltklinkenmaschinen
Beide Funktionsprinzipien gehen auf den bedeutendsten deutschen Rechenmaschinenkonstrukteur Christel Hamann (1870–1948) zurück. Das Proportionalhebelprinzip hatte Hamann in den Jahren 1902 und 1903 entwickelt. Das erste Exemplar seiner auf diesem Prinzip beruhenden Rechenmaschine Euklid wurde 1908 verkauft.
Die erste Schaltklinkenmaschine Hamann-Manus wurde ab 1925 von der Berliner Firma DeTeWe produziert. Die äußere Form der Schaltklinkenmaschinen war den am Markt etablierten Brunsviga-Sprossenradmaschinen angeglichen, um Benutzern den Umstieg auf diesen neuen Maschinentyp zu erleichtern.
Beide Funktionsprinzipien fanden nicht die Verbreitung des Sprossenrads und der Staffelwalze.
Multiplikationskörperrechenmaschinen

Multiplikationskörperrechenmaschinen haben als zentrales Funktionselement einen Einmaleinskörper, auf dem alle Produkte des kleinen Einmaleins in Stäben unterschiedlicher Länge repräsentiert sind.
Mit der Idee eines Multiplikationskörpers soll sich schon Leibniz befasst haben. Der in New York lebende Spanier Ramón Verea (1838–1899) entwickelte 1878 eine Multiplikationskörperrechenmaschine, von der vermutlich nur ein Prototyp gebaut wurde. In den Jahren 1888 bis 1892 baute der französische Automobilkonstrukteur und Erfinder Léon Bollée (1870–1913) drei Modelle von Rechenmaschinen mit einem Einmaleinskörper, die jedoch recht unhandlich in der Bedienung waren. Der Schweizer Otto Steiger konstruierte eine in größeren Stückzahlen produzierte Maschine: Seine Millionär wurde von 1893 bis ca. 1935 gebaut.
Buchungsmaschinen und Registrierkassen
Buchungsmaschinen sind Büromaschinen, mit denen man Belege über Geschäftsvorfälle verarbeiten kann. Sie entwickelten sich aus Schreibmaschinen und Rechenmaschinen.
Obwohl zu Buchungsmaschinen und Registrierkassen meist auch die Funktion des maschinellen Rechnens gehört, werden sie im Allgemeinen nicht zu den Rechenmaschinen gezählt.
Spezielle mechanische Rechenmaschinen
Es gibt viele Geräte, die für spezielle mathematische Aufgaben konstruiert wurden. Wichtige Vertreter sind der Mechanismus von Antikythera, die Differenzmaschinen des Engländers Charles Babbage (1791–1871) und der Schweden Georg und Edvard Scheutz.
Ausstellungen von Rechenmaschinen
Das Arithmeum in Bonn besitzt historisch genaue und funktionierende Replikate der Rechenmaschinen von Wilhelm Schickard, Blaise Pascal, Samuel Morland, Gottfried Wilhelm Leibniz, Anton Braun, Giovanni Poleni, Philipp Matthäus Hahn, Johann Helfrich von Müller, Charles Stanhope, Johann Christoph Schuster, Jacob Auch und Ramón Verea.
Das Heinz Nixdorf MuseumsForum in Paderborn widmet einen Ausstellungsbereich dem Rechnen von einfachen Rechenhilfmitteln bis hin zur Taschenrechnerwand mit aktuellen Modellen. Neben Replikaten und seltenen Maschinen ist erwähnenswert, dass in der Ausstellung auf Original-Maschinen aus den 1920er Jahren gerechnet werden darf.
Das Deutsche Museum in München hat einen großen Fundus von Rechenmaschinen. Da es das Deutsche Museum Anfang des zwanzigsten Jahrhunderts schon gab, sind in der Ausstellung viele Originalmaschinen zu sehen, die von den Herstellern damals zur Verfügung gestellt wurden. Insbesondere finden sich auch sehr wertvolle Unikate etwa von Philipp Matthäus Hahn oder Eduard Selling.
Das Museum Enter in Solothurn hat ebenfalls einen großen Fundus von funktionstüchtigen mechanischen Rechenmaschinen von Pascaline bis Curta.
Siehe auch
Einzelnachweise
- Die erste Rechenmaschine. Abgerufen am 13. März 2019.
- ▷VIDEO: Meisterwerke der Kunst: Pascaline. In: museumsfernsehen. 3. Juni 2016, abgerufen am 13. März 2019 (deutsch).
- Jan-Willem Liebezeit: Leibniz-Rechenmaschinen.
- http://www.math.tu-dresden.de/wir/staff/ludwig/sammlung/poster.pdf S. 11
- Korte, S. 23–30
- Silvio Hénin: Two early Italian key-driven calculators. IEEE Annals of the History of Computing 32.1 (2010).
- Max Detlefsen: Polnische Rechenmaschinenerfinder des 19. Jahrhunderts. Ein wenig bekanntes Kapitel polnischer Wissenschaftsgeschichte. In: wissenschaft und fortschritt, 26 (1976), Nr. 2, S. 86–90, hier S. 87–89 (PDF).
- Denis Roegel: Before Torchi and Schwilgué, There Was White. IEEE Annals of the History of Computing 38.4 (2016), S. 92–93.
- Rechnerlexikon – Odhner
- Walther – Die Firma und die Rechner. rechenkasten.de, abgerufen am 27. Juni 2020.
- Rechnerlexikon: Walther Multa 32. Abgerufen am 31. Juli 2012.
- Ulrich Fritsch: Die neue Dimension. Zukunftsstrategien internationaler Top-Manager, Düsseldorf, Wien 1986, S. 138: „1952 gründete Heinz Nixdorf in Essen das Labor für Impulstechnik“
- Friden EC-130 Electronic calculator (1963)
- Tätigkeitsbericht eines Schweizer Ingenieurs in Kalifornien (engl.).
- computermuseum.informatik.uni-stuttgart.de IME 84
- computermuseum.informatik.uni-stuttgart.de Sanyo ICC 82-D
- www.schlepptops.de Druckende Tischrechner ohne Anzeige
Literatur
- Herbert Bruderer: Meilensteine der Rechentechnik. Band 1: Mechanische Rechenmaschinen, Rechenschieber, historische Automaten und wissenschaftliche Instrumente. 2., stark erweiterte Auflage. Walter de Gruyter, Berlin/Boston 2018, ISBN 978-3-11-051827-6.
- Bruno Baron von Freytag-Löringhoff: Wilhelm Schickards Tübinger Rechenmaschine von 1623. 5., erw. Auflage, bearb. von Friedrich Seck. Univ.-Stadt Tübingen, Kulturamt, Tübingen 2002, ISBN 3-910090-48-6 (= Reihe Kleine Tübinger Schriften, Heft 4).
- Bernhard Korte: Die Rechenmaschine von Johann Christoph Schuster 1820/22. Kulturstiftung der Länder, Berlin 2004 (= Patrimonia 203).
- Bernhard Korte: Zur Geschichte des maschinellen Rechnens. Rede zur 57. Hauptversammlung der Gesellschaft von Freunden und Förderern der Rhein. Friedrich-Wilhelms-Univ. Bonn (GEFFRUB) am 14. Juni 1980. Bouvier, Bonn 1981 (= Bonner akademische Reden, Nr. 54).
- Karl Lenz: Die Rechenmaschinen und das Maschinenrechnen. Teubner, Leipzig und Berlin 1915.
- Ludolf von Mackensen: Die ersten dekadischen und dualen Rechenmaschinen. In: Erwin Stein, Albert Heinekamp (Hrsg.): Gottfried Wilhelm Leibniz – Das Wirken des großen Philosophen und Universalgelehrten als Mathematiker, Physiker, Techniker. Gottfried-Wilhelm-Leibniz-Gesellschaft, Hannover 1990, ISBN 3-9800978-4-6, S. 52–61.
- Ernst Martin: Die Rechenmaschine und ihre Entwicklungsgeschichte. Köntopp, Leopoldshöhe 1925.
- Walther Meyer zur Capellen: Mathematische Instrumente. 3., erg. Aufl., Akadem. Verlagsges., Leipzig 1949.
- Martin Reese: Neue Blicke auf alte Maschinen. Zur Geschichte mechanischer Rechenmaschinen. Kovac, Hamburg 2002, ISBN 3-8300-0533-4 (Reihe Technische Forschungsergebnisse, Bd. 8).
- A. Hennemann (d. i. Adolf Schranz): Die technische Entwicklung der Rechenmaschine. Basten, Aachen 1952.
- Adolf G. Schranz: Addiermaschinen. Einst- und jetzt. Basten, Aachen 1952.
- Friedrich Seck (Hrsg.): Wilhelm Schickard 1592–1635. Astronom, Geograph, Orientalist, Erfinder der Rechenmaschine. Mohr, Tübingen 1978, ISBN 3-16-939772-9.
- Historische Bürowelt. Vierteljahres-Zeitschrift des IFHB seit 1982
Weblinks
- Erhard Anthes: Mathematisches Maschinen-Museum im WorldWideWeb. Institut für Mathematik und Informatik an der Pädagogischen Hochschule Ludwigsburg.
- Rechnerlexikon. Die große Enzyklopädie des mechanischen Rechnens.
- Nachbau der Schickardschen Rechenmaschine im Rechnerlexikon.
- Patent-Datenbank mechanischer Rechenmaschinen im Rechnerlexikon.
- Reinhard Atzbach: Rechenwerkzeug.de Grafische und mechanische Rechenhilfen von der Antike bis ins Computerzeitalter.
- ISER Informatik-Sammlung Erlangen des Rechenzentrums Erlangen und des Instituts für Informatik der Friedrich-Alexander Universität Erlangen-Nürnberg.
- Günter Schwaninger: Die mechanischen Rechner (Calcorex, Facit, Piccolo).
- The Old Calculator Web Museum.
- Lebendiges Museum technikum 29 in Kelkheim/Taunus: Mechanisches Rechnen.
- Andreas Bauer, Wolfgang Weigel: Interaktive Sprossenradmaschine (Flash).
- Ernst Martin: The Calculating Machines (Die Rechenmaschinen). Their History and Development (PDF-Datei; 6,68 MB). Englische Übersetzung von Die Rechenmaschine und ihre Entwicklungsgeschichte.