Papyrus Rhind

Der Papyrus Rhind ist eine altägyptische, auf Papyrus verfasste Abhandlung zu verschiedenen mathematischen Themen, die wir heute als Arithmetik, Algebra, Geometrie, Trigonometrie und Bruchrechnung bezeichnen. Er gilt neben dem etwas älteren, aber weniger umfangreichen Papyrus Moskau 4676 als eine der wichtigsten Quellen für unser Wissen über die Mathematik im Alten Ägypten und wird auf etwa 1550 v. Chr.[1][2] datiert.

Linkes Ende der Vorderseite des größten Fragments des Papyrus Rhind (heute im British Museum, pBM 10057)

Wiedergabe des in der oberen Abbildung rechts sichtbaren Textabschnitts

Verwendung verschiedenfarbiger Tinte in dem (von rechts nach links) in hieratischer Schrift verfassten Manuskript – hier beim 41. Problem (Vergrößerung der Abbildung per Klick)

Einige Zeilen unter einer Skizze

Transkription dieser Zeilen unter der Skizze zum 48. Problem

Entdeckung

Der Papyrus Rhind ist benannt nach dem schottischen Anwalt und Antiquar Alexander Henry Rhind, der ihn 1858 in Luxor, Oberägypten erwarb. Die Schriftstücke wurden wohl wenig zuvor bei illegalen Grabungen auf dem gegenüber von Luxor westlich des Nils liegenden Gebiet Thebens in oder nahe dem Ramesseum gefunden, genauere Umstände sind nicht bekannt.[1]

Details

Der Papyrus wurde vermutlich im 16. Jahrhundert v. Chr. noch während der Zweiten Zwischenzeit angefertigt – einleitend wird das 33. Regierungsjahr des Apopi, eines Königs der 15. Dynastie der Hyksos, als Datum angegeben[1] – und wird in wesentlichen Teilen als die Kopie eines über zwei Jahrhunderte älteren Papyrus angesehen, welcher wahrscheinlich aus der Regierungszeit des Amenemhet III. der 12. Dynastie im Mittleren Reich stammte. Der Kopist – ein Schreiber namens Ahmose, nach einer früheren Transkription auch Ahmes – gebrauchte die hieratische Schrift und hob einige Werte und aufgeführte Verfahren mit roter anstelle von schwarzer Tinte hervor, so beispielsweise Sätze von Teilern.

Heute liegt der Papyrus nurmehr in Form von Fragmenten einer über 5 Meter langen und etwa 32 cm breiten Schriftrolle vor, die beidseitig beschrieben ist. Im British Museum werden zwei Stücke von 295,5 cm und 199,5 cm Länge verwahrt (1865 inventarisiert mit Nr. 10057 bzw. 10058); die Lücke zwischen beiden wird auf annähernd 18 cm geschätzt. Der Papyrus gibt neben einigen Tabellen eine Reihe verschiedener mathematischer Probleme mit beispielhaften Lösungen wieder; insgesamt sind es je nach Zählweise 84 oder 87 oder 91 Aufgaben. Der Text konnte erst am Ende des 19. Jahrhunderts n. Chr. entziffert und übersetzt werden, seine mathematischen Aussagen werden seit Anfang des 20. Jahrhunderts entschlüsselt und erschlossen.[2]

Inhaltlich lässt sich das Manuskript in drei Abteilungen gliedern. Nach dem Titel findet sich im ersten Teil zu Beginn eine längere Tabelle, die für alle ungeraden Zahlen n von 3 bis 101 den Bruch ²/_n als eine Summe von Stammbrüchen darstellt, gefolgt von einer kurzen Tabelle für n von 2 bis 9 des Bruchs ⁿ/₁₀. Anschließend werden 40 arithmetische und algebraische Probleme behandelt. Der zweite Teil stellt 20 geometrische Probleme vor und behandelt Rauminhalte und Flächeninhalte unterschiedlicher Figuren sowie das Verhältnis von Höhe zu Seite des Körpers einer Pyramide als deren Neigung. Zwei Dutzend weitere Probleme bilden den dritten Teil, neben Berechnungen bezogen auf die Herstellung von Brot und Bier wie auch auf die Fütterung von Geflügel und Rindern wird hier unter anderem eine Rätselaufgabe zu Katzen und Mäusen wiedergegeben.

Näherungswert für den Flächeninhalt eines Kreises

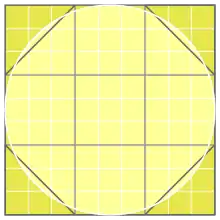
Ein Kreis in einem Quadrat, das durch ein Gitter zerlegt wird.
Der Kreisdurchmesser ist so lang wie eine Seite des umfassenden Quadrates – beträgt er 9, hat ein kleines Quadrat die Seitenlänge 3.

Zu den im zweiten Teil des Papyrus Rhind behandelten Problemen gehören auch Flächenberechnungen eines Kreises. In der 48. Aufgabenstellung beschreibt Ahmes, wie er die Fläche eines Kreises berechnet, der einem Quadrat eingeschrieben ist. Aus heutiger Sicht lässt sich dies als Angabe einer Näherung der Kreiszahl $\pi$ auffassen. Auf Grundlage der im Papyrus neben einer Skizze angegebenen Rechenvorschrift (siehe vierte und fünfte Abbildung von oben)[3] rekonstruierte Kurt Vogel 1928 die dahinterstehenden Überlegungen.[4]

Ahmes drittelt zunächst die Seiten des Quadrats und gewinnt damit neun gleiche kleinere Quadrate mit der Seitenlänge von 3 Einheiten. Dann schneidet er von den vier Eckzellen jeweils die Hälfte weg und kommt darüber zu der Figur eines unregelmäßigen Achtecks. Dieses Achteck setzt sich aus fünf vollen und vier halben zu der Gesamtfläche von 7 der kleinen Quadrate mit je 3² = 9 Flächeneinheiten zusammen und besitzt so den Flächeninhalt von 7•9 = 63 Quadrateinheiten. Es ist offensichtlich nur etwas kleiner als der Kreis – für dessen Fläche nimmt Ahmes daher den Inhalt von 64 = 8•8 Quadrateinheiten an, was nicht kleiner ist.

Somit wird die Fläche eines Kreises mit dem Durchmesser 9 gleich der Fläche eines Quadrates mit der Seitenlänge 8 gesetzt. Daraus ergibt sich näherungsweise für den Inhalt $A_{K}$ der Kreisfläche mit dem Halbmesser $r$ von ⁹⁄₂

über

A_{K}=r^{2}\cdot \pi

also

(9/2)^{2}\cdot \pi \approx 8^{2}

und damit annähernd

\pi \approx {\frac {8^{2}}{(9/2)^{2}}}=\left({\frac {16}{9}}\right)^{2}\approx 3{,}16049..

Der so ermittelte Wert verfehlt die Zahl $\pi$ (pi) absolut um etwa 0,01890 und relativ um weniger als ein Prozent (0,602 %). Im altägyptischen Zahlensystem wird dieser Wert nicht dezimal dargestellt, sondern als eine Summe von Stammbrüchen:

\left({\frac {16}{9}}\right)^{2}={\frac {256}{81}}=3+{\frac {1}{9}}+{\frac {1}{27}}+{\frac {1}{81}}\approx \pi

Für das im Papyrus Rhind wiedergegebene Verfahren kann die Annäherung an die Kreiszahl $\pi$ also aus dem Verhältnis der Flächeninhalte eines eingeschriebenen Kreises und seines umschreibenden Quadrates errechnet werden,

da

A_{Q}=r^{2}\cdot 4

, so denn

{\frac {A_{K}}{A_{Q}}}={\frac {\pi r^{2}}{(2r)^{2}}}={\frac {\pi }{4}}

und somit

\pi =4\cdot {\frac {A_{K}}{A_{Q}}}\approx 4\cdot {\frac {64}{81}}

Der einem Quadrat mit 81 Flächeneinheiten eingeschriebene Kreis umfängt tatsächlich etwa 63,617 Flächeneinheiten. In Approximation wird hier durch die von Ahmes aufgeschriebene Methode ein Kreis auf ein Quadrat von 9•9 bezogen, über eine achteckige Figur vermittelt und seine Fläche einem Quadrat von 8•8 gleichgesetzt – was wohl als früher Versuch einer Quadratur des Kreises angesehen werden kann. Die Flächengleichheit eines Quadrats mit einer Kreisfläche wurde demnach angenommen, wenn dessen Seitenlänge ⁸/₉ ihres Durchmessers beträgt, also um ein Neuntel geringer ist.

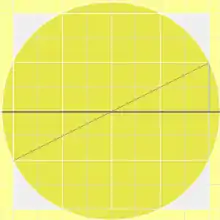
Ein Kreis kann in ein orthogonales Gitter so eingezeichnet werden, dass die umfangende Kreislinie acht Gitterpunkte schneidet, die Viertelungspunkte der Seiten eines Quadrats sind, das der Kreisfläche nahezu flächengleich scheint.
Im Falle eines 8×8-Quadrats, mit 64 Flächeneinheiten, misst der Kreisdurchmesser ungefähr 9 Längeneinheiten.

Doch der Bezug von Konturen einer Figur in einem orthogonalen Netz von Linien war schon den altägyptischen Steinmetzen geläufig, um einen Entwurf anhand der Verhältnisse von Schnittpunkten auf die zu bearbeitende Steinfläche proportioniert zu übertragen. Vor diesem Hintergrund stellte Hermann Engels 1977 eine andere Vermutung vor, mit der das hier angegebene näherungsweise Verhältnis aufgrund des Planquadratnetzes zu erklären wäre.[5] Danach würde man intuitiv einen Kreis C (mit Durchmesser d) so einzeichnen, dass sein Mittelpunkt der eines etwa flächengleichen Quadrats F (mit Seitenlänge a) aus 4 × 4 Teilquadraten ist, das in den Viertelungspunkten seiner Seiten von diesem Kreis achtmal geschnitten wird. Bei Übergang zu einer noch feineren Unterteilung von F (in 8 × 8 einheitliche Teilquadrate) erhält man für den Inhalt des Quadrats F also 64 solcher Flächeneinheiten, während der Kreisinhalt tatsächlich etwa 62,8 Flächeneinheiten beträgt – und einem Quadrat U mit 80 Flächeneinheiten exakt einzuschreiben ist –, denn

das Dreieck Mittelpunkt-Halbierungspunkt-Viertelungspunkt setzt Kreisradius und Quadratseite in die Beziehung

r^{2}=({\frac {a}{2}})^{2}+({\frac {a}{4}})^{2}=5\,({\frac {a}{4}})^{2}

und

mit

d=2r=2({\sqrt {5}}\cdot {\frac {a}{4}})\approx 1{,}118\;a

für den Durchmesser ergibt sich

aus

A_{C}=\pi r^{2}=\pi ({\sqrt {5}}\cdot {\frac {a}{4}})^{2}=\pi \cdot {\frac {5\,a^{2}}{16}}\approx 0{,}982\;a^{2}

dann

bei

a=8

Längeneinheiten somit für

A_{C}=20\,\pi \approx 62{,}832..

Flächeneinheiten,

sowie für

d^{2}=4r^{2}=4\cdot 5\,({\frac {8}{4}})^{2}=80

, also

{\frac {A_{C}}{A_{U}}}={\frac {20\,\pi }{80}}={\frac {\pi }{4}}

beziehungsweise

{\frac {A_{C}}{r^{2}}}={\frac {20\,\pi }{20}}=\pi .

Doch beträgt der Durchmesser weniger als 9 bei einem Kreis C, der in ein Quadrat U von 80 Flächeneinheiten (hellgelb) einzuschreiben ist.
Dass dieses Quadrat flächengleich ist der Summe aus Quadrat F (64) plus einem 4×4-Quadrat (16), mag ein Vergleich der (grauen bzw. gelben) Teilflächen nahelegen – Pythagoras war dieser Zusammenhang bekannt.

Bei einer irrtümlichen Annahme, dass der Kreis C flächengleich mit dem Quadrat F wäre, beträgt der Fehler für die Angabe der Kreisfläche („64 Einheiten“) knapp zwei Prozent (1,825 %). Betrachtet man dagegen den tatsächlichen Inhalt der konstruierten Kreisfläche und nimmt dann hinsichtlich der Beziehung von Seitenlänge zu Durchmesser,

bei

a=8

ergibt sich

d=4\cdot {\sqrt {5}}\approx 8{,}944

, also

d\approx 9

, näherungsweise mit der Schätzung

a\approx {\frac {8}{9}}\,d

vorlieb, so verfehlt man damit

r^{2}

um ungefähr 1,234 % – genau um ¹/₈₁ – denn

(9/2)^{2}=20,25

statt 20 Flächeneinheiten.

Wendet man alsdann für $\pi$ den oben beschriebenen Näherungswert von $(16/9)^{2}$ an, wird der tatsächliche Flächeninhalt von $A_{C}=r^{2}\cdot \pi =20\,\pi$ (≈ 62,832) mit der Annäherung $A\approx (9/2)^{2}\cdot (16/9)^{2}$ etwas zu hoch veranschlagt – doch das Ergebnis entspricht nun der falschen Annahme: „64 Einheiten“.

Auf die Weise erhielte man aus der Anschauung eines Kreises in einem Quadratnetz, wie es für eine Übertragung von Entwürfen auf zu bearbeitende Flächen üblich war, in recht einfacher Art – bei irriger Annahme und grobem Maß – eine schlichte Rechenregel für die Kreisfläche: „Vermindere den Kreisdurchmesser um ein Neuntel, so bekommst du die Seite des Quadrats.“[5] – die oft erstaunlich gut zutrifft.

Das abschätzend angesetzte Verhältnis von ⁸⁄₉ wird auch im Problem 41 (siehe dritte Abbildung von oben, vergrößert) des Papyrus Rhind angewandt, wo es um die Berechnung des Volumens eines zylindrischen Kornspeichers geht. Ebenfalls wird es in der Berechnungsvorschrift für den Flächeninhalt einer gekrümmten Oberfläche angenommen, die im Problem 10 des älteren Papyrus Moskau 4676 wiedergegeben ist; hier gehen allerdings die Interpretationen schon darüber auseinander, welche Fläche genau gemeint ist.[6]

Aufbewahrungsort

Die beiden Hauptstücke des Papyrus Rhind (Rhind Mathematical Papyrus (RMP)), ein knapp 3 m und ein knapp 2 m langes Fragment, befinden sich seit 1865 im Besitz des Britischen Museums in London, verzeichnet unter den Inventarnummern pBM 10057 bzw. pBM 10058.[1] Von dem fehlenden Zwischenstück (knapp 0,2 m) sind einige kleinere Fragmente erhalten, die damals nicht von Rhind erworben wurden und heute im Brooklyn Museum in New York aufbewahrt werden.[7]

Siehe auch

Ausgaben

August Eisenlohr: Ein mathematisches Handbuch der alten Aegypter (Papyrus Rhind des British Museum). 2 Bände, Hinrichs, Leipzig 1877 (online).
Thomas Eric Peet: The Rhind Mathematical Papyrus, British Museum 10057 and 10058. Hodder & Stoughton für The University Press of Liverpool, London 1923.
Arnold Buffum Chace, Henry Parker Manning, Raymond C. Chace, Ludlow Bull: The Rhind Mathematical Papyrus: British Museum 10057 and 10058. 2 Bände, Mathematical Association of America, Oberlin [OH], 1927/ 1929. (Verkürzte Neuauflage: National Council of Teachers of Mathematics, Reston [OH] 1979, ISBN 0-87353-133-7).
Gay Robins, Charles Shute: The Rhind Mathematical Papyrus. An Ancient Egyptian Text. British Museum, London 1987, ISBN 0-7141-0944-4 (mit Fotos des Papyrus).

Literatur

Marshall Clagett: Ancient Egyptian Science. A Source Book. Band 3: Ancient Egyptian Mathematics (= Memoirs of the American Philosophical Society. 232). American Philosophical Society, Philadelphia PA 1999, ISBN 0-87169-232-5.
Milo Gardner: An Ancient Egyptian Problem and its Innovative Arithmetic Solution. In: Gaṇita-Bhāratī. Bulletin of the Indian Society for the History of Mathematics. Band 28, 2006, ISSN 0970-0307, S. 157–173.
Richard J. Gillings: Mathematics in the time of the pharaohs. Unabridged, slightly corrected republication. Dover Publications, New York NY 1982, ISBN 0-486-24315-X.
Annette Imhausen: Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten (= Ägyptologische Abhandlungen. 65). Harrassowitz, Wiesbaden 2003, ISBN 3-447-04644-9.
Franz von Krbek: Eingefangenes Unendlich. Bekenntnis zur Geschichte der Mathematik. 2. Auflage. Geest & Portig, Leipzig 1954, S. 79 ff.
Neil MacGregor: Eine Geschichte der Welt in 100 Objekten. (Aus dem Englischen von Waltraut Götting, Andreas Wirthensohn, Annabell Zettel). Beck u. a., München 2011, ISBN 978-3-406-62147-5, S. 141–149.

Weblinks

Commons: Rhind Mathematical Papyrus – Sammlung von Bildern, Videos und Audiodateien

Rhind Mathematical Papyrus – Artikel mit Abbildungen der Papyrus-Fragmente auf Site des British Museum.
Eric W. Weisstein: Rhind Papyrus. MathWorld–A Wolfram Web Resource. Abgerufen am 29. Januar 2011.
O’Connor and Robertson: Mathematics in Egyptian Papyri.
Scott W. Williams: Egyptian Mathematics Papyri.
RMP 2/n Table der englischen Wikipedia

Einzelnachweise

The Rhind Papyrus. in der Collection des British Museum. Abgerufen am 6. Juli 2021.
Annette Imhausen: Mathematics in Ancient Egypt. A Contextual History. Princeton University Press, Princeton NJ u. a. 2020, ISBN 978-0-691-20907-4, S. 65 f., (google book).
vergleiche die fotografische Wiedergabe dieser Stelle des Rhind mathematical papyrus im Internetauftritt des British Museum.
siehe dazu Kurt Vogel: Vorgriechische Mathematik. Teil 1: Vorgeschichte und Ägypten (= Mathematische Studienhefte für den mathematischen Unterricht an höheren Schulen. 1, ZDB-ID 255205-X). Schroedel u. a., Hannover 1958, S. 66.
Hermann Engels: Quadrature of the circle in ancient Egypt. In: Historia Mathematica. Band 4, Nr. 2, 1977, S. 137–140, doi:10.1016/0315-0860(77)90104-5.
Hans Wußing: 6000 Jahre Mathematik. Eine kulturgeschichtliche Zeitreise. Band 1: Von den Anfängen bis Leibniz und Newton. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0, S. 120 f., (eingeschränkte Online-Version (Google Books)).
Fragments of Rhind Mathematical Papyrus. online in der Collection des Brooklyn Museum. Abgerufen am 29. August 2016.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[british-1] The Rhind Papyrus. in der Collection des British Museum. Abgerufen am 6. Juli 2021.

[imhausen-2] Annette Imhausen: Mathematics in Ancient Egypt. A Contextual History. Princeton University Press, Princeton NJ u. a. 2020, ISBN 978-0-691-20907-4, S. 65 f., (google book).

[3] vergleiche die fotografische Wiedergabe dieser Stelle des Rhind mathematical papyrus im Internetauftritt des British Museum.

[4] siehe dazu Kurt Vogel: Vorgriechische Mathematik. Teil 1: Vorgeschichte und Ägypten (= Mathematische Studienhefte für den mathematischen Unterricht an höheren Schulen. 1, ZDB-ID 255205-X). Schroedel u. a., Hannover 1958, S. 66.

[engels-5] Hermann Engels: Quadrature of the circle in ancient Egypt. In: Historia Mathematica. Band 4, Nr. 2, 1977, S. 137–140, doi:10.1016/0315-0860(77)90104-5.

[6] Hans Wußing: 6000 Jahre Mathematik. Eine kulturgeschichtliche Zeitreise. Band 1: Von den Anfängen bis Leibniz und Newton. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0, S. 120 f., (eingeschränkte Online-Version (Google Books)).

[brooklyn-7] Fragments of Rhind Mathematical Papyrus. online in der Collection des Brooklyn Museum. Abgerufen am 29. August 2016.