Eudoxos von Knidos

Eudoxos von Knidos (griechisch Εὔδοξος Eúdoxos; * wohl zwischen 397 und 390 v. Chr. in Knidos; † wohl zwischen 345 und 338 v. Chr. in Knidos) war ein griechischer Mathematiker, Astronom, Geograph, Arzt, Philosoph und Gesetzgeber der Antike. Seine Werke sind bis auf Fragmente verloren. Daher sind seine wissenschaftlichen Leistungen nur aus Berichten anderer Autoren bekannt bzw. zu erschließen. Mit seiner mathematischen Darstellung der Himmelskörperbewegungen leistete er einen maßgeblichen Beitrag zur Geometrisierung der Astronomie. In der Mathematik begründete er die allgemeine Proportionenlehre.

Leben

Die überlieferte chronologische Einordnung der Lebenszeit des Eudoxos ist unrichtig. Der Doxograph Diogenes Laertios zitiert hierzu eine Mitteilung des Apollodoros von Athen, aus der sich für die Geburt der Zeitraum von 407 bis 404 ergibt und für den Tod, da Eudoxos in seinem 53. Lebensjahr gestorben sein soll, der Zeitraum 355 bis 352. Dies kann aber nicht zutreffen, da Eudoxos in einem seiner Werke bei einer Zeitangabe ausdrücklich auf den 348/347 eingetretenen Tod Platons Bezug nimmt.[1] Da er Platon überlebt hat, fällt seine Geburt vermutlich ungefähr in den Zeitraum 397–390, sein Tod ungefähr in den Zeitraum 345–338.

Eudoxos stammte aus bescheidenen Verhältnissen. Seine Heimatstadt Knidos war seit dem 5. Jahrhundert v. Chr. für ihre medizinische Schule, die mit derjenigen von Kos rivalisierte, berühmt. Angeblich studierte er bei Archytas von Tarent Mathematik und bei Philistion von Lokroi Medizin.[2] Für ein Schülerverhältnis zu Archytas, der in Tarent lebte, müsste aber ein längerer Studienaufenthalt in Italien angenommen werden, was in der Forschung bezweifelt wird; die Überlieferung zu einer angeblichen Sizilienreise gilt als unglaubwürdig.[3] Im Alter von etwa 23 Jahren ging er nach Athen, da der Ruf der dort lehrenden Sokratiker ihn anzog. Dieser erste Aufenthalt in Athen dauerte nur zwei Monate und führte wohl zu seiner ersten Begegnung mit Platon. Einer von Diogenes Laertios mitgeteilten Nachricht zufolge weigerte sich Platon zunächst, ihn als Schüler anzunehmen, doch berichtet der von Diogenes zitierte Doxograph Sotion von Alexandria, er habe an Lehrveranstaltungen Platons teilnehmen können. Jedenfalls kehrte Eudoxos bald nach Knidos zurück.

Um 365/364 reiste Eudoxos in Begleitung eines Mitbürgers, des Arztes Chrysippos,[4] nach Ägypten. Ein Empfehlungsschreiben des Königs Agesilaos II. von Sparta ebnete ihm den Weg zum Pharao Nektanebos I. Der Aufenthalt dauerte sechzehn Monate. Sein besonderes Interesse galt den Kenntnissen der ägyptischen Priester, in deren Astronomie er sich Einblick verschaffte. Nach der Rückkehr aus Ägypten begab er sich nach Kyzikos an der Südküste des Marmarameers, wo er Unterricht erteilte. Von dort aus besuchte er den einflussreichen, für kulturelle Belange aufgeschlossenen persischen Satrapen Maussolos.

Später übersiedelte er mit einer beträchtlichen Anzahl seiner Schüler nach Athen. Dort soll er einer umstrittenen Überlieferung zufolge als Lehrer mit Platon rivalisiert haben.[5] Ob er in die Platonische Akademie eintrat und inwieweit er als Platoniker bezeichnet werden kann und seinerseits Platon beeinflusste, ist nicht eindeutig feststellbar. Jedenfalls bestand ein Kontakt zur Akademie, der wahrscheinlich eng war.[6] Nach einem Bericht, der auf Aristoxenos von Tarent zurückgeht, trat Aristoteles „unter Eudoxos“ oder „zur Zeit des Eudoxos“ in die Akademie ein. Diese Formulierung ist in der älteren Forschung so gedeutet worden, dass der Eintritt des Aristoteles erfolgte, als Platon sich auf seiner zweiten Sizilienreise befand, und dass Eudoxos als Stellvertreter Platons die Akademie leitete.[7] Das ist jedoch nicht plausibel, da Eudoxos damals noch jung war und noch nicht lange in der Akademie mitgearbeitet haben kann, falls er ihr tatsächlich jemals angehörte.[8]

Nach dem Aufenthalt in Athen begann Eudoxos wieder eine eigenständige Lehrtätigkeit, vermutlich wiederum in Kyzikos. Später kehrte er nach Knidos zurück. Dort betätigte er sich als Gesetzgeber für seine Mitbürger, bei denen er sich hohen Ansehens erfreute; auch überregional fand er Anerkennung. Er ließ in Knidos ein Observatorium bauen.

Zu den Schülern des Eudoxos gehörten der Arzt Chrysippos, der ihn nach Ägypten begleitete, die Mathematiker Menaichmos und Deinostratos und der Astronom Polemarchos von Kyzikos.

Diogenes Laertios erwähnt, Eudoxos habe drei Töchter und einen Sohn namens Aristagoras gehabt.

Werke

Obwohl Eudoxos seine bedeutendsten Leistungen auf dem Gebiet der Geometrie vollbrachte, ist kein einziger Titel eines einschlägigen Werkes überliefert. Seine mathematischen Entdeckungen sind daher nur aus Schriften anderer Autoren bekannt. Von philosophischen Werken ist nichts überliefert; möglicherweise hat er keine verfasst, sondern seine Auffassungen nur mündlich dargelegt.

Eudoxos verfasste mehrere astronomische Schriften, die nur aus Erwähnungen bzw. Wiedergaben ihres Inhalts in späterer Literatur bekannt sind:

„Phänomene“ (Phainómena), sein erstes astronomisches Werk. Eine überarbeitete Fassung nannte er „Spiegel“ (Énoptron; gemeint: Spiegel der Weltordnung). Die Schrift bestand aus drei Büchern. Das erste enthielt eine Beschreibung der relativen Positionen der Gestirne, das zweite behandelte ihre Positionen bezogen auf die Himmelskugel und deren Einteilungen, im dritten befand sich ein Katalog von Gestirnen mit Angaben über den jeweiligen Aufgang und Untergang. Erhalten ist das berühmte Gedicht „Phänomene und Zeichen“ des Aratos von Soloi, das im ersten Teil eine freie Übertragung der „Phänomene“ des Eudoxos in Verse enthält.
„Über Geschwindigkeiten“ (Peri tachōn), seine astronomische Hauptschrift, in der er die Bewegungen der Planeten erklärte. Unter „Planeten“ („Wandelgestirnen“) verstand man damals Mond, Sonne, Venus, Merkur, Mars, Jupiter und Saturn; die Planeten jenseits des Saturn waren noch nicht bekannt. Eudoxos ging von seinem geozentrischen Weltbild aus, das auf der Annahme einer unbeweglichen Erde beruht, um die sich die Kugelschalen (Sphären) drehen, die den beweglichen Himmelskörpern und den Fixsternen zugeordnet sind. Mit den im Titel angesprochenen Geschwindigkeiten sind die verschiedenen Umdrehungsgeschwindigkeiten der Sphären gemeint. Aristoteles beschreibt das System des Eudoxos knapp in seiner Metaphysik.
„Über das durch die Sonne bewirkte Erlöschen“ (Peri aphanismōn hēliakōn). Hier legte Eudoxos seine Methode dar, mit welcher der Zeitpunkt des Aufgangs und Untergangs eines Sterns bestimmt wird, wenn das Sonnenlicht eine genaue Beobachtung unmöglich macht.
„Der achtjährige Zyklus“ (Oktaetērís), worin Eudoxos einen astronomischen Kalender erläuterte, der auf einem achtjährigen Zyklus basiert. Es scheint sich um das älteste so betitelte Werk über dieses später oft erörterte Thema zu handeln, doch ist unklar, ob der überlieferte Titel von Eudoxos stammt. Sein ursprüngliches Werk ist nur teilweise rekonstruierbar; Eratosthenes hielt eine ihm vorliegende Fassung, die in der Antike viel Beachtung fand, mit Recht für nicht authentisch.
Astronomía, ein astronomischer Kalender in Versen, der von den Gestirnen handelnde Sagen enthielt. Dieses Lehrgedicht war ein Spätwerk.

Nicht von Eudoxos stammt der ihm früher zugeschriebene Traktat Eudoxi ars astronomica, der auf Papyrus erhalten ist. Diese Abhandlung enthält jedoch unter anderem Material zur Astronomie und Kalenderrechnung, das auf ihn zurückgeht.

Auf geographischem Gebiet verfasste Eudoxos eine literarisch gestaltete „Erdbeschreibung“ (Gēs períodos), die zu seinen Spätwerken zählt. Darin behandelte er auch kulturgeographische Themen.[9]

Wovon die Eudoxos zugeschriebenen Schriften handelten, die Diogenes Laertios als „Hundedialoge“ (Kynōn diálogoi) bezeichnet, ist unbekannt. Diogenes beruft sich auf Eratosthenes und ergänzt, nach Angaben anderer Autoren seien diese Dialoge von Ägyptern in deren Sprache verfasst worden und Eudoxos habe sie nur ins Griechische übersetzt. Letzteres würde entsprechende Sprachkenntnisse des Eudoxos voraussetzen und ist daher angezweifelt worden.[10]

Philosophie

Über zwei Stellungnahmen des Eudoxos zu philosophischen Fragen liegt ein Bericht des Aristoteles vor. Die eine betrifft die Ideenlehre, die andere die Lehre vom Guten. In beiden Fragen vertritt Eudoxos eine Auffassung, die derjenigen Platons fundamental widerspricht.

Ideenlehre

Vermutlich hat Eudoxos keine eigene Ideenlehre entwickelt, sondern nur aus gegebenem Anlass eine Einzelfrage der Ideenlehre erörtert, wobei es ihm möglicherweise nur um eine hypothetische Erwägung ging. Das Problem war die Frage, wie die Teilhabe der Einzeldinge an den Ideen zustande kommt. Eudoxos meinte, es mit einer Mischungslehre lösen zu können; die Ideen seien den wahrnehmbaren Objekten beigemischt. Aristoteles vergleicht dies mit der Beimischung einer Farbe zum von ihr Gefärbten. Ungewiss ist, ob dieser Vergleich auf Eudoxos zurückgeht. Wie Eudoxos sich die Mischung vorgestellt hat, ist unklar; anscheinend ging er von einem naturphilosophischen, bei den Vorsokratikern gängigen Mischungsbegriff aus und nahm im Gegensatz zu Platon eine örtliche Anwesenheit der Ideen in den Dingen an. Im Gegensatz zu Aristoteles wollte er zugleich an Platons Lehre einer von den Dingen abgetrennten Existenz der Ideen festhalten. Dies trug ihm den Vorwurf der Widersprüchlichkeit ein. Die überlieferte Gegenargumentation lautet, dass er die Ideen materialisiere und in die Vergänglichkeit der materiellen Welt einbeziehe und dass sie dabei ihre Einfachheit und Unwandelbarkeit verlören. Dadurch würden sie ihren spezifischen ontologischen Status einbüßen, wären also keine Ideen im Sinne der platonischen Ideenlehre mehr.[11]

Ethik

In der Ethik vertrat Eudoxos bei der Bestimmung des Guten eine hedonistische Position. Er setzte das Gute mit der Freude gleich. Dabei argumentierte er, die Freude werde von allen Wesen – vernünftigen und vernunftlosen – angestrebt; sie sei daher das allgemeine Gute, das Gute schlechthin. Sie werde im Unterschied zu anderen Gütern nicht gelobt, da sie über allen lobenswerten Gütern stehe. Da sie um ihretwillen erstrebt werde und nicht um eines anderen Gutes willen, komme ihr ein höherer Rang zu als den Gütern, die zu einem bestimmten Zweck als wünschenswert erscheinen. Jedes Gut, dem sie beigefügt werde, werde dadurch begehrenswerter; daher sei sie das wahre Gute, nämlich das, was nicht durch etwas anderes gewinnt, sondern nur durch sich selbst.[12] Umstritten ist, ob Eudoxos auch die Überzeugung vertrat, das Lustprinzip gehöre zum Wesen der Gottheit und daher ziele das Luststreben, das in allen Lebewesen im Kosmos ein und dasselbe sei, letztlich auf die Gottheit, in der die höchste Lust verwirklicht sei.[13]

Mathematik

Eudoxos begründete die allgemeine Proportionenlehre. Dabei konnte er erstmals die irrationalen Größen einbeziehen, da seine Proportionenlehre auch auf inkommensurable Größen anwendbar ist. Seine Definitionen von Verhältnis (lógos) und Proportion (analogía) sind im fünften Buch von Euklids Elementen überliefert.

In der Forschung ist vermutet worden, dass das nach Archimedes benannte Archimedische Axiom in Wirklichkeit von Eudoxos stammt. Die Ausgangsproblematik hat Eudoxos offenbar gekannt, doch inwieweit er sich damit auseinandergesetzt hat, ist unklar.[14]

Er untersuchte die Volumenverhältnisse von Körpern und zeigte, dass das Volumen einer Pyramide einem Drittel des entsprechenden Prismas und dasjenige eines Kegels einem Drittel des entsprechenden Zylinders entspricht. Für seinen Beweis verwendete er ein infinitesimales Berechnungsverfahren, die Exhaustionsmethode. Mit dieser Methode konnte er auch das Verhältnis der Kreisfläche und des Kugelvolumens zum Radius bestimmen.

Eudoxos befasste sich mit dem in der Antike intensiv diskutierten Problem der Würfelverdoppelung („Delisches Problem“). Er fand dafür eine nicht näher bekannte Lösung durch den Schnitt von Kurven; deren Schnittpunkte ergaben die zur Lösung des Problems erforderlichen zwei mittleren Proportionalen zur Kante des gegebenen und der des gesuchten Würfels.[15] Ferner erfand Eudoxos, wie Plutarch berichtet, auch eine mechanische Vorrichtung zur annähernden Konstruktion von zwei mittleren Proportionalen.

Astronomie und Geographie

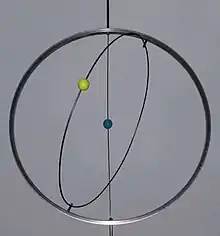
Modell mit zwei Sphären (hier Ringe) für die Darstellung der Bewegungen der Sonne relativ zur Erde

In der Astronomie ging es Eudoxos darum, die im Rahmen seines geozentrischen Weltbildes unregelmäßig erscheinenden Bewegungen der Planeten mit Stillständen und Rückläufen mathematisch darzustellen. Angeblich hatte Platon die Forschungsaufgabe gestellt, die Planetenumläufe auf regelmäßige Kreisbewegungen zurückzuführen.[16] Für jeden Planeten sowie für Sonne und Mond nahm Eudoxos ein eigenes System konzentrischer Kugelschalen (Sphären) an, die mit verschiedenen Geschwindigkeiten und in verschiedenen Richtungen gleichförmig um gegeneinander geneigte Achsen rotieren. Wegen des gemeinsamen Zentrums – der Erde – spricht man von der Theorie der homozentrischen Sphären. Jeder Himmelskörper ist am Äquator der innersten ihm zugeordneten Schale fixiert. Die zu einem Himmelskörper gehörenden Schalen sind an ihren Polen aneinander befestigt. Dadurch übertragen sich ihre Bewegungen auf die innerste Schale und damit auf das Gestirn. Den fünf ihm bekannten Planeten wies Eudoxos je vier Sphären zu, der Sonne und dem Mond je drei. Die jeweils erste (äußerste) Planetensphäre bewirkt den Tagesumlauf des Planeten von Ost nach West, die zweite seine Jahresbahn im Tierkreis von West nach Ost, die dritte und die vierte erzeugen zusammen die (scheinbare) achtförmige Schleifenbewegung, die Eudoxos „Hippopede“ (Pferdefessel) nannte.[17] Für die Fixsterne genügte eine Sphäre. Damit kam Eudoxos auf insgesamt 27 Sphären. Die Frage nach einem Zusammenhang der einzelnen Sphärensysteme untereinander stellte sich für ihn nicht, denn seine Konzeption war eine rein mathematische, nicht physikalisch fundierte Hypothese, die komplexe Verhältnisse in einfache Elemente (regelmäßige Kreisbewegungen) auflöste.[18]

In der Forschung wird teils vermutet, teils bestritten, dass Eudoxos bereits die später verbreitete Forderung der „Rettung der Phänomene“ zu erfüllen trachtete und sogar deren Urheber im Sinne der Formulierung eines Forschungsprinzips war. Die genaue Bedeutung dieses Ausdrucks ist umstritten. Einer Deutung zufolge ging es ursprünglich darum, die scheinbaren Bewegungen der Himmelskörper als Folge ihrer wahren Bewegungen aufzuweisen. Erst später habe man unter „Rettung der Phänomene“ den Grundsatz verstanden, dass von einer Theorie nur zu verlangen sei, dass die mit ihr durchgeführten Berechnungen mit jedem Beobachtungsresultat übereinstimmen, und nicht, dass sie physikalische Realität wahrheitsgemäß wiedergibt.[19] Nach einer anderen Deutung war mit dem „Retten“ der Phänomene gemeint, eine mathematische Beschreibung, die vorgegebenen physikalischen oder naturphilosophischen Annahmen gerecht werden soll, nachträglich so abzuwandeln oder zu ergänzen, dass sie „die Phänomene rettet“, d. h. bestimmte Phänomene, die in ihrem Rahmen als Anomalien erscheinen, ebenfalls berücksichtigt.[20]

Das System des Eudoxos ermöglichte nur Näherungslösungen und berücksichtigte nicht alle damals bekannten Anomalien der Himmelskörperbewegungen. Daher wurde es später von Kallippos von Kyzikos, der weitere Sphären hinzufügte, erweitert.

Eine wichtige Schwäche des Systems bestand darin, dass es die Helligkeitsschwankungen der Planeten, die auf Änderung ihrer Entfernung von der Erde schließen lassen, nicht erklären konnte. Darauf wies in der Spätantike der Aristoteles-Kommentator Simplikios hin.[21]

Eudoxos bestimmte auch die Abstände und Größenverhältnisse von Erde, Mond und Sonne. Wie er dabei vorging, ist unbekannt.[22] Die Reihenfolge der beweglichen Himmelskörper war bei ihm die damals gängige: von innen nach außen Mond, Sonne, Venus, Merkur, Mars, Jupiter, Saturn.

Ferner soll er den Erdumfang ermittelt haben. Aristoteles gibt mit Berufung auf „Mathematiker“, die er nicht namentlich nennt, einen Erdumfang von 400.000 Stadien an. Bei dieser viel zu hohen Zahl handelt es sich wohl um eine Schätzung; die erste überlieferte Berechnung ist diejenige des Eratosthenes aus dem 3. Jahrhundert v. Chr. Die von Aristoteles mitgeteilte Schätzung wird oft Eudoxos zugeschrieben, doch gibt es dafür keinen Beleg.[23]

Cicero berichtet, Eudoxos habe als erster die Sternbilder auf einem Himmelsglobus eingetragen, nachdem schon Thales eine solche Kugel angefertigt hatte.[24] Demnach war Eudoxos nicht der Erfinder des Himmelsglobus, aber der erste, der die Gestirne kartographisch auftrug.

Einem bei Vitruv überlieferten Katalog von Erfindungen zufolge galt Eudoxos als Erfinder einer aráchnē („Spinne“). Mit diesem Begriff bezeichnete man in späterer Zeit die bewegliche Scheibe eines flachen Astrolabiums (einer zweidimensionalen Darstellung der Himmelskugel). Diese rotierende Scheibe bildete den Fixsternhimmel ab und konnte dessen tägliche Drehung wiedergeben. Ein solches Astrolabium existierte allerdings zur Zeit des Eudoxos noch nicht. Seine arachne war wohl eine Vorstufe, eine durchsichtige Scheibe, die den Hauptbestandteil einer Sternenuhr bildete. Sie trug eine Abbildung des Fixsternhimmels, die einem Spinngewebe ähnelte.[25]

Als Geograph befasste sich Eudoxos insbesondere mit der Einteilung der Erde in Klimazonen. Er zeichnete eine Karte der in der gemäßigten Zone der Nordhalbkugel liegenden Oikumene (des bekannten, besiedelten Teils der Erdoberfläche). Für ihn hatte die Oikumene die Form eines Rechtecks, das doppelt so lang wie breit war.[26] Die Grenze bildete im Westen die Iberische Halbinsel, im Osten Indien, im Süden Äthiopien und im Norden das Gebiet der Skythen. Im Süden schloss sich an die gemäßigte Zone die „verbrannte Zone“ an, deren nördliche Hälfte bis zum Äquator reichte. Auf der Südhalbkugel waren die klimatischen Verhältnisse spiegelbildlich. Dort nahm er in der südlichen gemäßigten Klimazone, in welcher der Nil entspringe, eine der Oikumene analoge, ebenfalls bewohnte Gegenoikumene an.[27] Die geographische Breite (énklima) einer Region bestimmte er nach dem Verhältnis des längsten Tages zum kürzesten oder zur kürzesten Nacht; ob er sie schon in Breitengraden berechnet hat, ist ungewiss. Für seinen Ort kam er auf ein Verhältnis von 5 : 3; ein anderes von ihm ermitteltes Ergebnis lautete 12 : 7. Unklar ist, ob die beiden Angaben sich auf verschiedene Orte beziehen oder die eine als Berichtigung der anderen aufzufassen ist. Bei seinen Messungen verwendete er ein Gnomon, einen senkrechten Stab, dessen Schatten in der horizontalen Ebene beobachtet wird. Aus dem Verhältnis des kürzesten und des längsten Mittagsschattens, die an den beiden Sonnenwenden zu beobachten waren, ergab sich das gesuchte Verhältnis.[28]

Rezeption

Antike

Inwieweit Platons Dialog Philebos als antihedonistische Antwort auf die Argumentation des Eudoxos für die Gleichsetzung des Guten mit der Freude oder Lust gedacht war, ist unklar; in der Forschung gehen die Meinungen darüber auseinander.[29]

Aristoteles ging in seiner Nikomachischen Ethik kritisch auf Eudoxos’ Lustlehre ein. Dabei stieß er auf die Schwierigkeit, dass die Gedankengänge des Eudoxos teilweise Argumenten, die er selbst anderenorts vorbrachte, sehr ähnlich waren, die daraus gefolgerte Gleichsetzung des Guten mit der Lust aber für ihn nicht akzeptabel war, da er das Streben der „Vielen“ nach Genuss für vulgär und tierisch hielt. Daher behalf er sich mit einem Argument ad hominem: Eudoxos habe mit seinen Argumenten nicht wegen deren Überzeugungskraft Anklang gefunden, sondern wegen seines eigenen Charakters, der so gut gewesen sei, dass man ihn nicht verdächtigt habe, einen vulgären Hedonismus zu verteidigen.[30] Grundsätzlich teilte Aristoteles aber die Überzeugung des Eudoxos, dass der normative Grundbegriff „Gut“ handlungstheoretisch als „das Ziel, zu dem alles strebt“ zu bestimmen sei. Möglicherweise übernahm er die Gleichsetzung des (wirklichen oder vermeintlichen) Guten mit dem Erstrebten, die er an den Anfang der Nikomachischen Ethik stellte, von Eudoxos.[31] In seinem verlorenen Werk „Über die Ideen“ brachte Aristoteles im Rahmen seiner Kritik an der platonischen Ideenlehre auch Argumente gegen die Ideenlehre des Eudoxos vor.

Euklid nahm in seine Elemente eine Reihe von Erkenntnissen des Eudoxos auf. Dabei handelte es sich um die Proportionenlehre und deren geometrische Anwendungen sowie Volumenbestimmungen.

Das Planetensystem des Eudoxos blieb in der erweiterten Version des Kallippos in der griechischen Astronomie maßgeblich, bis es ab Ende des 3. Jahrhunderts v. Chr. von der Epizykeltheorie verdrängt wurde. Insbesondere prägte es die astronomischen Vorstellungen des Aristoteles. Aristoteles versuchte, das mathematische Modell physikalisch zu fundieren, indem er die Sphären als reale materielle Gegebenheiten auffasste, ihre Anzahl noch erhöhte und davon ausging, dass sie alle miteinander verbunden seien.[32] So beeinflusste Eudoxos über die Aristoteles-Rezeption indirekt noch das physikalische Weltbild des Mittelalters.

Die „Phänomene“ fanden bei vielen antiken Autoren Beachtung. Verwendet wurden sie unter anderem von Philippos von Opus, Aratos von Soloi und Geminos von Rhodos; Vitruv hatte nur indirekten Zugang über eine Zwischenquelle. Aratos dichtete eine Versfassung. Im 2. Jahrhundert v. Chr. verfasste der Astronom Hipparchos von Nikaia einen kritischen Kommentar zu den „Phänomenen“ des Eudoxos und zu der Versfassung des Aratos.

Strabon rühmt die geographische Kompetenz des Eudoxos. Er berichtet, der Geschichtsschreiber Polybios habe Eudoxos’ Darstellung der historischen Geographie geschätzt; dazu zählten Gründungsgeschichten griechischer Städte sowie Informationen über die Abstammungsverhältnisse von deren Bevölkerungen und über Wanderungsbewegungen. Als Strabon 25/24 v. Chr. oder bald danach Ägypten bereiste, zeigte man ihm in Heliopolis Räume, in denen sich Eudoxos angeblich aufgehalten hatte.[33] Diese Legende war Bestandteil einer ägyptischen Propaganda, welche griechische Weisheit und Wissenschaft auf ägyptische Wurzeln zurückführte. Seneca meinte, Eudoxos habe die Kenntnis der Planetenbewegungen aus Ägypten nach Griechenland gebracht.[34]

Philostratos betrachtet Eudoxos als rednerisch begabten Philosophen und Vorläufer der „zweiten Sophistik“. Diogenes Laertios bewertet seine Werke als außerordentlich wertvoll.

Moderne

In der modernen Forschung hat Eudoxos außerordentlich starke Beachtung gefunden. Insbesondere sein Sphärensystem wird seit dem 19. Jahrhundert von Astronomiehistorikern intensiv diskutiert. 1828–1830 legte der Astronom Christian Ludwig Ideler einen Rekonstruktionsversuch vor, 1849 brachte eine Untersuchung von Ernst Friedrich Apelt weitere Erkenntnisse. Die 1877 veröffentlichte Rekonstruktion des Astronomen Giovanni Schiaparelli erwies sich als bahnbrechend. Sie dominierte bis ins späte 20. Jahrhundert und gilt noch heute als „klassisch“, hat aber Schwächen, die zur Entstehung von alternativen Hypothesen geführt haben.[35]

1935 wurde der Mondkrater Eudoxus, 1973 der Marskrater Eudoxus und 1998 der Asteroid (11709) Eudoxos nach Eudoxos benannt.[36]

Textausgaben

François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos. De Gruyter, Berlin 1966 (kritische Ausgabe mit Kommentar; vgl. die sehr kritische Rezension von Gerald J. Toomer in: Gnomon. Bd. 40, 1968, S. 334–337).

Literatur

David R. Dicks: Early Greek Astronomy to Aristotle. Thames and Hudson, London 1970, ISBN 0-500-40013-X, S. 151–189.
Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles. Erlangen 1988 (Dissertation).
Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3). 2., durchgesehene und erweiterte Auflage, Schwabe, Basel 2004, ISBN 3-7965-1998-9, S. 56–66, 146–149.
Jean-Pierre Schneider: Eudoxe de Cnide. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques. Band 3, CNRS Éditions, Paris 2000, ISBN 2-271-05748-5, S. 293–302.
Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles. Das Fortwirken der Eudoxischen Proportionentheorie in der Aristotelischen Lehre vom Kontinuum. Grüner, Amsterdam 1977, ISBN 90-6032-086-7.

Weblinks

Literatur von und über Eudoxos von Knidos im Katalog der Deutschen Nationalbibliothek
John J. O’Connor, Edmund F. Robertson: Eudoxus of Cnidus. In: MacTutor History of Mathematics archive. [teilweise überholter Forschungsstand]
Don Allen: Eudoxus of Cnidus (1997) [biographische Angaben nur teilweise korrekt]

Anmerkungen

Siehe hierzu François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 137–139, 254 f.; Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977, S. 34–40; Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles, Erlangen 1988, S. 8–15.
Diogenes Laertios 8,8,86 und 8,8,89.
François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 146; weniger skeptisch ist Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 57. Philip Merlan: Studies in Epicurus and Aristotle, Wiesbaden 1960, S. 100 hält die Reise für historisch.
Dieser Chrysippos war möglicherweise ein Verwandter des berühmten Arztes Chrysippos von Knidos, mit dem er nicht zu verwechseln ist. Zur Datierung François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 139 f.
Diogenes Laertios 8,8,87.
Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 57; Jean-Pierre Schneider: Eudoxe de Cnide. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Bd. 3, Paris 2000, S. 293–302, hier: 297.
So denken Kurt von Fritz: Die Ideenlehre des Eudoxos von Knidos und ihr Verhältnis zur platonischen Ideenlehre. In: Kurt von Fritz: Schriften zur griechischen Logik, Bd. 1, Stuttgart 1978, S. 147–169, hier: 167 und Philip Merlan: Studies in Epicurus and Aristotle, Wiesbaden 1960, S. 99.
Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977, S. 41–52; Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 159 f.
Siehe zu diesem Werk John Gardiner-Garden: Eudoxos, Skylax and the Syrmatai. In: Eranos 86, 1988, S. 31–42, hier: 31 f. und den ausführlichen Rekonstruktionsversuch von Friedrich Gisinger: Die Erdbeschreibung des Eudoxos von Knidos, Berlin 1921, S. 15 ff.
François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 269; anderer Meinung sind Joachim Quack: Die Rolle der Hieroglyphen in der Theorie vom griechischen Vokalalphabet. In: Wolfgang Ernst, Friedrich Kittler (Hrsg.): Die Geburt des Vokalalphabets aus dem Geist der Poesie, München 2006, S. 75–98, hier: 88 f. und John Gwyn Griffiths: A Translation from the Egyptian by Eudoxus. In: The Classical Quarterly N.S. 15, 1965, S. 75–78.
Zu Eudoxos’ Ideenkonzept siehe Kurt von Fritz: Die Ideenlehre des Eudoxos von Knidos und ihr Verhältnis zur platonischen Ideenlehre. In: Kurt von Fritz: Schriften zur griechischen Logik, Bd. 1, Stuttgart 1978, S. 147–169; François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 149–151; Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 59–61; Russell M. Dancy: Two Studies in the Early Academy, Albany 1991, S. 23–56; Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 157–161.
Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 64–66; François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 13 f., 151–156; Heinrich Karpp: Untersuchungen zur Philosophie des Eudoxos von Knidos, Würzburg 1933, S. 6–27.
Diese Hypothese vertritt Wolfgang Schadewaldt: Hellas und Hesperien, 2. Auflage, Bd. 1, Zürich und Stuttgart 1970, S. 644–655. Zu anderen Auffassungen siehe François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 156 f.
Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977, S. 308–318.
François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 20–22, 163–166.
Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 63 hält diese umstrittene Nachricht für glaubwürdig; ebenso Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 166. Zu den Vertretern der gegenteiligen Auffassung zählt Jürgen Mittelstraß: Die Rettung der Phänomene, Berlin 1962, S. 1–4, 150–155.
Zum Sphärenmodell siehe Friedrich Heglmeier: Die griechische Astronomie zur Zeit des Aristoteles. Ein neuer Ansatz zu den Sphärenmodellen des Eudoxos und des Kallippos. In: Antike Naturwissenschaft und ihre Rezeption, Bd. 6, 1996, S. 51–71, hier: 53–61; Erkka Maula: Studies in Eudoxus’ Homocentric Spheres, Helsinki 1974, S. 14 ff. Zur Hippopede siehe John D. North: The Hippopede. In: Anton von Gotstedter (Hrsg.): Ad radices, Stuttgart 1994, S. 143–154.
Dies ist die traditionelle und weiterhin herrschende Lehrmeinung in der Forschung. Eine Gegenposition vertritt Larry Wright: The Astronomy of Eudoxus: Geometry or Physics? In: Studies in History and Philosophy of Science, Bd. 4, 1973/74, S. 165–172. Er meint, Eudoxos habe eine Beschreibung und Erklärung der tatsächlichen physikalischen Gegebenheiten angestrebt.
Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 62 f.; Leonid Zhmud: »Saving the phenomena« between Eudoxus and Eudemus. In: Gereon Wolters, Martin Carrier (Hrsg.): Homo Sapiens und Homo Faber, Berlin 2005, S. 17–24; Martin Carrier: Die Rettung der Phänomene. Zu den Wandlungen eines antiken Forschungsprinzips. In: Gereon Wolters, Martin Carrier (Hrsg.): Homo Sapiens und Homo Faber, Berlin 2005, S. 25–38.
Fritz Krafft: Der Mathematikos und der Physikos. In: Alte Probleme – Neue Ansätze, Würzburg 1964, S. 5–24. Krafft meint, dass die Aufgabe, Phänomene (Anomalien) zu „retten“, sich für Eudoxos noch nicht stellte.
Siehe dazu Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 302 und Anm. 3; Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles, Erlangen 1988, S. 242.
François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 17, 211.
Klaus Geus: Eratosthenes von Kyrene. Studien zur hellenistischen Kultur- und Wissenschaftsgeschichte, München 2002, S. 226 Anm. 86.
Cicero, De re publica 1,14,22.
François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 158–160. Für andere Deutungen der arachne siehe Bernard R. Goldstein, Alan C. Bowen: A New View of Early Greek Astronomy. In: Isis Bd. 74, 1983, S. 330–340, hier: 335–337; Erkka Maula: The Spider in the Sphere. Eudoxus’ Arachne. In: Philosophia (Athen) Bd. 5/6, 1975/76, S. 225–258.
François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 239 f.; Friedrich Gisinger: Die Erdbeschreibung des Eudoxos von Knidos, Berlin 1921, S. 13 f.
Stephan Heilen: Eudoxos von Knidos und Pytheas von Massalia, in: Wolfgang Hübner (Hrsg.): Geschichte der Mathematik und der Naturwissenschaften in der Antike, Bd. 2: Geographie und verwandte Wissenschaften, Stuttgart 2000, S. 55–73, hier: 58–60.
Árpád Szabó: Eudoxos und das Problem der Sehnentafeln. In: Jürgen Wiesner (Hrsg.): Aristoteles. Werk und Wirkung, Bd. 1, Berlin 1985, S. 499–517, hier: 502–510. Eine Gegenposition zu dieser herrschenden Lehrmeinung vertreten Alan C. Bowen und Bernard R. Goldstein: Hipparchus’ Treatment of Early Greek Astronomy. The Case of Eudoxus and the Length of Daytime. In: Proceedings of the American Philosophical Society Bd. 135, 1991, S. 233–254. Sie bezweifeln, dass die genannten Zahlen auf Messungen oder Beobachtungen beruhen, und halten es für möglich, dass die beiden Verhältnisse arithmetisch aus theoretischen Erwägungen abgeleitet wurden.
Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 66; Justin C.B. Gosling, Christopher C.W. Taylor: The Greeks on Pleasure, Oxford 1982, S. 157–164; Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 161–166; skeptisch ist Dorothea Frede: Platon: Philebos. Übersetzung und Kommentar, Göttingen 1997, S. 390–394.
Aristoteles, Nikomachische Ethik 1172b; vgl. 1095b. Siehe dazu Roslyn Weiss: Aristotle’s Criticism of Eudoxan Hedonism. In: Classical Philology Bd. 74, 1979, S. 214–221.
Aristoteles, Nikomachische Ethik 1094a; siehe dazu Franz Dirlmeier: Aristoteles: Nikomachische Ethik, 8. Auflage, Berlin 1983, S. 266 f.; Otfried Höffe: Aristoteles, 2. Auflage, München 1999, S. 202 f.
Siehe dazu Friedrich Heglmeier: Die griechische Astronomie zur Zeit des Aristoteles. Ein neuer Ansatz zu den Sphärenmodellen des Eudoxos und des Kallippos. In: Antike Naturwissenschaft und ihre Rezeption, Bd. 6, 1996, S. 51–71, hier: 69 f.
Zu Strabons Eudoxos-Rezeption siehe Johannes Engels: Die strabonische Kulturgeographie in der Tradition der antiken geographischen Schriften und ihre Bedeutung für die antike Kartographie. In: Orbis Terrarum Bd. 4, 1998, S. 63–114, hier: 73–76.
Seneca, Naturales quaestiones 7,3,2.
Zur Wissenschaftsgeschichte siehe Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles, Erlangen 1988, S. 69–89. Zu den alternativen Lösungsversuchen siehe Ido Yavetz: On the Homocentric Spheres of Eudoxus. In: Archive für History of Exact Sciences 52, 1998, S. 221–278; Ido Yavetz: A New Role for the Hippopede of Eudoxus. In: Archive für History of Exact Sciences 56, 2002, S. 69–93.
lunar photo of the day 26. März 2010; 11709 Eudoxos (1998 HF20) JPL Small-Body Database Browser.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Siehe hierzu François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 137–139, 254 f.; Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977, S. 34–40; Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles, Erlangen 1988, S. 8–15.

[2] Diogenes Laertios 8,8,86 und 8,8,89.

[3] François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 146; weniger skeptisch ist Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 57. Philip Merlan: Studies in Epicurus and Aristotle, Wiesbaden 1960, S. 100 hält die Reise für historisch.

[4] Dieser Chrysippos war möglicherweise ein Verwandter des berühmten Arztes Chrysippos von Knidos, mit dem er nicht zu verwechseln ist. Zur Datierung François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 139 f.

[5] Diogenes Laertios 8,8,87.

[6] Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 57; Jean-Pierre Schneider: Eudoxe de Cnide. In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Bd. 3, Paris 2000, S. 293–302, hier: 297.

[7] So denken Kurt von Fritz: Die Ideenlehre des Eudoxos von Knidos und ihr Verhältnis zur platonischen Ideenlehre. In: Kurt von Fritz: Schriften zur griechischen Logik, Bd. 1, Stuttgart 1978, S. 147–169, hier: 167 und Philip Merlan: Studies in Epicurus and Aristotle, Wiesbaden 1960, S. 99.

[8] Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977, S. 41–52; Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 159 f.

[9] Siehe zu diesem Werk John Gardiner-Garden: Eudoxos, Skylax and the Syrmatai. In: Eranos 86, 1988, S. 31–42, hier: 31 f. und den ausführlichen Rekonstruktionsversuch von Friedrich Gisinger: Die Erdbeschreibung des Eudoxos von Knidos, Berlin 1921, S. 15 ff.

[10] François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 269; anderer Meinung sind Joachim Quack: Die Rolle der Hieroglyphen in der Theorie vom griechischen Vokalalphabet. In: Wolfgang Ernst, Friedrich Kittler (Hrsg.): Die Geburt des Vokalalphabets aus dem Geist der Poesie, München 2006, S. 75–98, hier: 88 f. und John Gwyn Griffiths: A Translation from the Egyptian by Eudoxus. In: The Classical Quarterly N.S. 15, 1965, S. 75–78.

[11] Zu Eudoxos’ Ideenkonzept siehe Kurt von Fritz: Die Ideenlehre des Eudoxos von Knidos und ihr Verhältnis zur platonischen Ideenlehre. In: Kurt von Fritz: Schriften zur griechischen Logik, Bd. 1, Stuttgart 1978, S. 147–169; François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 149–151; Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 59–61; Russell M. Dancy: Two Studies in the Early Academy, Albany 1991, S. 23–56; Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 157–161.

[12] Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 64–66; François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 13 f., 151–156; Heinrich Karpp: Untersuchungen zur Philosophie des Eudoxos von Knidos, Würzburg 1933, S. 6–27.

[13] Diese Hypothese vertritt Wolfgang Schadewaldt: Hellas und Hesperien, 2. Auflage, Bd. 1, Zürich und Stuttgart 1970, S. 644–655. Zu anderen Auffassungen siehe François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 156 f.

[14] Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977, S. 308–318.

[15] François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 20–22, 163–166.

[16] Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 63 hält diese umstrittene Nachricht für glaubwürdig; ebenso Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 166. Zu den Vertretern der gegenteiligen Auffassung zählt Jürgen Mittelstraß: Die Rettung der Phänomene, Berlin 1962, S. 1–4, 150–155.

[17] Zum Sphärenmodell siehe Friedrich Heglmeier: Die griechische Astronomie zur Zeit des Aristoteles. Ein neuer Ansatz zu den Sphärenmodellen des Eudoxos und des Kallippos. In: Antike Naturwissenschaft und ihre Rezeption, Bd. 6, 1996, S. 51–71, hier: 53–61; Erkka Maula: Studies in Eudoxus’ Homocentric Spheres, Helsinki 1974, S. 14 ff. Zur Hippopede siehe John D. North: The Hippopede. In: Anton von Gotstedter (Hrsg.): Ad radices, Stuttgart 1994, S. 143–154.

[18] Dies ist die traditionelle und weiterhin herrschende Lehrmeinung in der Forschung. Eine Gegenposition vertritt Larry Wright: The Astronomy of Eudoxus: Geometry or Physics? In: Studies in History and Philosophy of Science, Bd. 4, 1973/74, S. 165–172. Er meint, Eudoxos habe eine Beschreibung und Erklärung der tatsächlichen physikalischen Gegebenheiten angestrebt.

[19] Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 62 f.; Leonid Zhmud: »Saving the phenomena« between Eudoxus and Eudemus. In: Gereon Wolters, Martin Carrier (Hrsg.): Homo Sapiens und Homo Faber, Berlin 2005, S. 17–24; Martin Carrier: Die Rettung der Phänomene. Zu den Wandlungen eines antiken Forschungsprinzips. In: Gereon Wolters, Martin Carrier (Hrsg.): Homo Sapiens und Homo Faber, Berlin 2005, S. 25–38.

[20] Fritz Krafft: Der Mathematikos und der Physikos. In: Alte Probleme – Neue Ansätze, Würzburg 1964, S. 5–24. Krafft meint, dass die Aufgabe, Phänomene (Anomalien) zu „retten“, sich für Eudoxos noch nicht stellte.

[21] Siehe dazu Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 302 und Anm. 3; Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles, Erlangen 1988, S. 242.

[22] François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 17, 211.

[23] Klaus Geus: Eratosthenes von Kyrene. Studien zur hellenistischen Kultur- und Wissenschaftsgeschichte, München 2002, S. 226 Anm. 86.

[24] Cicero, De re publica 1,14,22.

[25] François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 158–160. Für andere Deutungen der arachne siehe Bernard R. Goldstein, Alan C. Bowen: A New View of Early Greek Astronomy. In: Isis Bd. 74, 1983, S. 330–340, hier: 335–337; Erkka Maula: The Spider in the Sphere. Eudoxus’ Arachne. In: Philosophia (Athen) Bd. 5/6, 1975/76, S. 225–258.

[26] François Lasserre (Hrsg.): Die Fragmente des Eudoxos von Knidos, Berlin 1966, S. 239 f.; Friedrich Gisinger: Die Erdbeschreibung des Eudoxos von Knidos, Berlin 1921, S. 13 f.

[27] Stephan Heilen: Eudoxos von Knidos und Pytheas von Massalia, in: Wolfgang Hübner (Hrsg.): Geschichte der Mathematik und der Naturwissenschaften in der Antike, Bd. 2: Geographie und verwandte Wissenschaften, Stuttgart 2000, S. 55–73, hier: 58–60.

[28] Árpád Szabó: Eudoxos und das Problem der Sehnentafeln. In: Jürgen Wiesner (Hrsg.): Aristoteles. Werk und Wirkung, Bd. 1, Berlin 1985, S. 499–517, hier: 502–510. Eine Gegenposition zu dieser herrschenden Lehrmeinung vertreten Alan C. Bowen und Bernard R. Goldstein: Hipparchus’ Treatment of Early Greek Astronomy. The Case of Eudoxus and the Length of Daytime. In: Proceedings of the American Philosophical Society Bd. 135, 1991, S. 233–254. Sie bezweifeln, dass die genannten Zahlen auf Messungen oder Beobachtungen beruhen, und halten es für möglich, dass die beiden Verhältnisse arithmetisch aus theoretischen Erwägungen abgeleitet wurden.

[29] Hans Krämer: Eudoxos aus Knidos. In: Hellmut Flashar (Hrsg.): Ältere Akademie – Aristoteles – Peripatos (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Bd. 3), 2. Auflage, Basel 2004, S. 56–66, hier: 66; Justin C.B. Gosling, Christopher C.W. Taylor: The Greeks on Pleasure, Oxford 1982, S. 157–164; Hermann Schmitz: Die Ideenlehre des Aristoteles, Bd. 2: Platon und Aristoteles, Bonn 1985, S. 161–166; skeptisch ist Dorothea Frede: Platon: Philebos. Übersetzung und Kommentar, Göttingen 1997, S. 390–394.

[30] Aristoteles, Nikomachische Ethik 1172b; vgl. 1095b. Siehe dazu Roslyn Weiss: Aristotle’s Criticism of Eudoxan Hedonism. In: Classical Philology Bd. 74, 1979, S. 214–221.

[31] Aristoteles, Nikomachische Ethik 1094a; siehe dazu Franz Dirlmeier: Aristoteles: Nikomachische Ethik, 8. Auflage, Berlin 1983, S. 266 f.; Otfried Höffe: Aristoteles, 2. Auflage, München 1999, S. 202 f.

[32] Siehe dazu Friedrich Heglmeier: Die griechische Astronomie zur Zeit des Aristoteles. Ein neuer Ansatz zu den Sphärenmodellen des Eudoxos und des Kallippos. In: Antike Naturwissenschaft und ihre Rezeption, Bd. 6, 1996, S. 51–71, hier: 69 f.

[33] Zu Strabons Eudoxos-Rezeption siehe Johannes Engels: Die strabonische Kulturgeographie in der Tradition der antiken geographischen Schriften und ihre Bedeutung für die antike Kartographie. In: Orbis Terrarum Bd. 4, 1998, S. 63–114, hier: 73–76.

[34] Seneca, Naturales quaestiones 7,3,2.

[35] Zur Wissenschaftsgeschichte siehe Friedrich Heglmeier: Die homozentrischen Sphären des Eudoxos und des Kallippos und der Irrtum des Aristoteles, Erlangen 1988, S. 69–89. Zu den alternativen Lösungsversuchen siehe Ido Yavetz: On the Homocentric Spheres of Eudoxus. In: Archive für History of Exact Sciences 52, 1998, S. 221–278; Ido Yavetz: A New Role for the Hippopede of Eudoxus. In: Archive für History of Exact Sciences 56, 2002, S. 69–93.

[36] unar photo of the day 26. März 2010; 11709 Eudoxos (1998 HF20) JPL Small-Body Database Browser.