Zahldarstellung

Zahldarstellung (auch Zahlendarstellung) bezeichnet ein Format zur Darstellung einer Zahl. Bekannt sind die Zahlschrift zur schriftlichen Darstellung, Zahlworte und Zahlennamen zur mündlichen Darstellung, aber auch eine (analoge) Zahldarstellung durch eine physikalische Größe wie Länge[1] oder Winkel ist möglich. Zahldarstellungen sind nicht beschränkt durch die in Zahlensystemen darstellbaren natürlichen Zahlen, so kann z. B. ein Computer durch eine Gleitkommazahl eine reelle Zahl approximativ darstellen.

Zahldarstellung im Unärsystem auf einer 25-Jahre Jubiläumskarte.

Einleitung

Je nach Einsatzgebiet gibt es vielfältige Zahldarstellungen, daher kann im Folgenden nur ein grober Überblick geboten werden. Einige Zahlen dienen als temporäre Zwischenergebnisse und haben daher für weitere Berechnungen optimierte Darstellungen, andere Darstellungen haben aufgrund ihrer Verarbeitungsgeschichte ein besonderes Format. Hinzu kommt, dass je nach Zahlbereich andere Darstellungen üblich sind.

Anzahl als Ansammlung von Zahlzeichen

Es ist einfach, eine Zahl durch die entsprechende Anzahl konkreter Gegenstände darzustellen[2]:

Steinchen, Muscheln, Perlen, Münzen (siehe Calculus)
Kerben auf einem Kerbholz
Striche in einer Strichliste
Finger (siehe auch Fingerrechnen)

Diese Gegenstände erfüllen dann die Funktion eines Zahlzeichens. Auch die Zahlworte einer gesprochenen Sprache können von Begriffen abstammen, in denen eine Anzahl enthalten war, z. B. „Sonne“ für eins, „Augen“ für zwei, „Tierpfoten“ für vier, „Hand“ für fünf.[2] Durch die Anordnung der Calculi auf dem Rechenbrett oder im Abakus können gleichartigen Calculi je nach Position verschiedene Zahlwerte zugeordnet werden – auf diese Weise wird das Rechnen in einfachen Zahlensystemen unterstützt. Auch durch unterscheidbare Typen der Gegenstände lassen sich größere Zahlen darstellen, wenn jedem Typ ein anderer Wert zugeordnet wird. So erlaubt Bargeld die Darstellung eines Geldbetrags als bloße Ansammlung von Münzen und Banknoten.

Schriftliche Darstellungen

Natürliche, ganze und rationale Zahlen

Die Zahlschrift ist wohl das wichtigste Mittel zur Zahldarstellung. Um die natürlichen Zahlen darzustellen, werden schriftliche Zahlzeichen nach den Regeln eines Zahlensystems zusammengesetzt. Zwecks kompakter Notation und Eignung für schriftliche Rechenverfahren (z. B. schriftliche Addition, schriftliche Multiplikation) wurden im Laufe der Menschheitsgeschichte verschiedene Zahlschriften verdrängt oder weiterentwickelt. Heute vorherrschend ist das Dezimalsystem mit arabischen Ziffern.

Durch ein vorangestelltes Vorzeichen können auch negative Zahlen, insgesamt also jede ganze Zahl dargestellt werden. Rationale Zahlen lassen sich als Brüche, also als Paare von ganzen Zahlen, schreiben. Diese Darstellung ermöglicht es, mit den vier Grundrechenarten exakt zu rechnen, auch der Zahlenvergleich ist entscheidbar. Mit dem vollständig gekürzten Bruch existiert sogar eine eindeutige Darstellung. Kommazahlen ermöglichen die Notation im Dezimalsystem für Stellenwerte kleiner Eins.

Darstellungen am Beispiel von 2,875
${\begin{aligned}2{,}875&=2\cdot 10^{0}+8\cdot 10^{-1}+7\cdot 10^{-2}+5\cdot 10^{-3}={\frac {2875}{1000}}\\&={\frac {5\cdot 5\cdot 5\cdot 23}{2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5}}={\frac {23}{8}}\end{aligned}}$

Irrationale und sonstige Zahlen

Nicht jede reelle Zahl lässt sich aufschreiben, da es nur abzählbar unendlich viele endliche Darstellungen über einem endlichen Alphabet gibt (die Überabzählbarkeit der reellen Zahlen gilt nach dem Diagonalargument). Dennoch lässt sich jede reelle Zahl im Stellenwertsystem mit unendlich vielen Nachkommastellen darstellen (im Dezimalsystem ist das eine unendliche Dezimalbruchentwicklung) – wenn die schriftliche Notation einer unendlichen Darstellung nicht naturgemäß unmöglich wäre. Daher kann hier nur auf die Abschnitte rein-mathematische Darstellungen und geometrische Darstellungen mittels Zahlengerade verwiesen werden.

Dass keine universelle schriftliche Notation bekannt ist, mag erstaunen, angesichts der recht einheitlichen heutigen Notationen:

Einige Zahlen werden standardmäßig als komplexe Ausdrücke unter Anwendung von Rechenoperatoren dargestellt (Bsp. ${\sqrt {2}}$ ).
Einige Konstanten werden durch ein spezielles Symbol dargestellt (Bsp. $\pi$ , $e$ ).
Komplexe Zahlen können dargestellt werden
- mithilfe der imaginären Einheit $\mathrm {i}$ (z. B. $3+2\mathrm {i}$ ),
- in Polarform mit Polarkoordinaten als $a\cdot e^{\mathrm {i} \phi }$ .
Auch physikalische Konstanten werden durch Symbole dargestellt (Bsp. $c$ ).
Die wissenschaftliche Notation ist eine Gleitkommadarstellung zur approximativen Darstellung aller reellen Zahlen.
Viele Zahlen können auch durch unendliche Reihen dargestellt werden, z. B.
- $\pi =4\cdot \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}$ (Leibniz-Reihe).

Sprachliche Darstellungen

Zahlwörter sind als Wortart feste Bestandteile der jeweiligen Sprache. Es handelt sich hierbei nicht um ein bloßes Aussprechen der Zahlschrift, auch die Zahlschrift ist nicht ein „Abschreiben“ der Sprache.[3] Eine Ausnahme bilden die chinesischen Zahlzeichen, wo die Schrift genau der Aussprache entspricht. Beispielsweise steht 四千八百七十九 für 4·1000+8·100+7·10+9 = 4879:[4]

Zeichen	四	千	八	百	七	十	九
Wert	4	1000	8	100	7	10	9
Übersetzung	vier	tausend	acht	hundert	sieb	zig	*neun

Diese Darstellung befolgt streng das von Georg Cantor als Gesetz der Größenfolge (GGF) bezeichnete Prinzip, so sind die Zehnerpotenzen 1000, 100, 10 und 1 in absteigender Reihenfolge angeordnet.[5] Die Übersetzung ist jedoch nicht „*sieb|zig|neun“, sondern „neun|und|sieb|zig“, durch die vertauschte Nennung von Einer- und Zehnerwerten wird das GGF im Deutschen somit verletzt. Ähnliche Inkonsequenzen finden sich in fast allen Sprachen.[5] Eine solche Inkonsequenz lässt sich auch an den Wörtern „elf“ und „zwölf“ festmachen, nicht „*einzehn“ und „*zweizehn“. Hier handelt es sich wohl um Überbleibsel eines Duodezimalsystems.

Die Zehnerpotenzen und somit die Größenordnungen werden explizit genannt, anders als in der gewohnten Zahlschrift, wo ein Blick auf die Anzahl der Stellen genügt („4879“ hat vier Stellen, also Größenordnung 1000). Die Wortbildung ist jedoch noch wesentlich mächtiger, so kann z. B. zwischen Kardinal- (eins, zwei, drei) und Ordinalzahlen (erstens, zweitens, drittens) direkt unterschieden werden. Bruchzahlen und somit die Darstellung rationaler Zahlen ermöglicht die Endsilbe „-tel“, z. B. „vierzehn siebenunddreißigstel“. Nachkommastellen werden hingegen ganz nach der Schrift ausgesprochen, beispielsweise wird 24,193 zu „vierundzwanzig Komma eins neun drei“.

Geometrische Darstellungen

Eine Analoguhr kann 12 Stunden und je 60 Minuten und Sekunden visuell darstellen.

Konstruktion von Wurzel 2 auf der Zahlengeraden

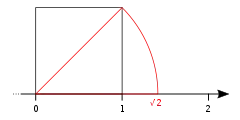
Eine „Grundvorstellung von den reellen Zahlen“ geht davon aus, dass jede reelle Zahl genau einem Punkt auf der lückenlosen Zahlengerade entspricht.[6] Demnach wären alle reellen Zahlen auf der Zahlengerade darstellbar. Da ferner die Grundrechenarten geometrisch konstruierbar sind, lässt sich die Konstruktion der reellen Zahlen mittels Intervallschachtelungen sehr gut veranschaulichen und rechtfertigen.

Andere Zahlbereiche, die Restklassen, könnte man nach dem Prinzip von Zahlenkreisen darstellen.[7] Der Wert einer Zahl entspricht dann dem Winkel. Die aus dem Alltag bekannte Analoguhr ist eine solche kreisförmige Darstellung, 12 Stunden und 60 Minuten können bezüglich der 12-Stunden-Zählung durch Uhrzeiger abgelesen werden.

Zur Darstellung der komplexen Zahlen wird die Zahlengerade zur komplexen Zahlenebene erweitert.

Darstellungen in Computern

Computerarithmetik gehörte immer schon zu den integralen Bestandteilen eines Computers. Aufgrund der endlichen Speichergröße sind allerdings die Möglichkeiten der Zahlendarstellung beschränkt. Ein relevantes Kriterium ist auch die Geschwindigkeit der arithmetischen Operationen bezüglich der jeweiligen Zahlendarstellung, um eine gute Ausführungsgeschwindigkeit eines Computerprogramms zu erreichen. Zwecks Optimierung werden diese Operationen oft in der arithmetisch-logischen Einheit berechnet, die nur binärkodierte Zahlen einer festen Wortgröße akzeptiert.

Wegen Speicherbegrenzung und Geschwindigkeitsoptimierung werden bestimmte Zahlendarstellungen von Programmierern bevorzugt: Integer mit beschränktem Wertebereich speichert ganze Zahlen. Rationale und reelle Zahlen werden oft durch Gleitkommazahlen ersetzt. Die beschränkten Darstellungsmöglichkeiten dieser Datentypen können jedoch zu arithmetischem Überlauf, Rundungsfehlern oder ähnlichen Rechenfehlern führen. Um auch mit größeren natürlichen Zahlen ohne Überlauf rechnen zu können, unterstützen moderne Programmiersprachen zusätzlich zum Datentyp Integer die Langzahlarithmetik, womit theoretisch beliebig große natürlichen Zahlen dargestellt werden können.

Auch für die reellen Zahlen gibt es Abhilfe, obwohl die Darstellung aller reellen Zahlen nicht möglich ist, da nur abzählbar viele Zahlen kodiert werden können. So erlaubt die Darstellung der algebraischen Zahlen Berechnungen ohne Rundungsfehler. Sollen jedoch transzendente Zahlen wie $\pi$ verwendet werden, helfen algebraische Zahlen nicht weiter. Oft muss eine Zahl gar nicht exakt berechnet werden: Es genügt dann, den Rundungsfehler abzuschätzen, Alltag in der numerischen Fehleranalyse. Dies kann z. B. durch Intervallarithmetik automatisiert werden. Prinzipiell ist auch die Darstellung aller berechenbaren Zahlen möglich.

Rein-mathematische Darstellungen

Einige Darstellungen sind zu umständlich für die Verwendung außerhalb der Mathematik, ermöglichen aber mathematische Eleganz und klare Beweisführungen. Andere Darstellungen wie die schon erwähnten unendlichen Dezimalbrüche sind abstrakte Erweiterungen der etablierten schriftlichen Darstellung ins Unendliche.

Bekannte Darstellungen reeller Zahlen beziehen sich selbst auf abstrakte Objekte, so ist für einen Dedekindschen Schnitt die Darstellung einer Partition bzw. Teilmenge der rationalen Zahlen nötig. In einer algebraischen Struktur kann eine Zahl wiederum durch die Verknüpfungen (also $+$ , $\cdot$ und $\leq$ ) mit anderen Zahlen innerhalb der Struktur indirekt dargestellt werden (eine algebraische Struktur kann axiomatisch definiert sein, z. B. können die reellen Zahlen axiomatisch als vollständig archimedisch-angeordneter Körper definiert werden)[8].

Beispiele

Darstellung einer natürlichen Zahl als …
- … Nachfolger des Nachfolgers des usw. der Null $0+1+\dotsb +1$ (korrespondiert mit den Peano-Axiomen), drei entspricht $0+1+1+1$ ,
- … Menge ohne Urelemente mit von Neumanns Modell, drei entspricht $\left\{\emptyset ,\left\{\emptyset \right\},\left\{\emptyset ,\left\{\emptyset \right\}\right\}\right\}$ .
Darstellung einer reellen Zahl als …
- … Cauchyfolge rationaler Zahlen,
- … Intervallschachtelung rationaler Zahlen,
- … Dedekindscher Schnitt mittels Partition rationaler Zahlen (eindeutig),
- … unendlicher Dezimalbruch (Kommazahlen mit unendlich vielen Stellen hinter dem Komma).
Darstellung allgemein …
- … bezüglich Verknüpfungen in einer algebraischen Struktur ( $0$ ist das eindeutige Element mit $x+x=x$ in jedem Ring).

Literatur

Georges Ifrah: Universalgeschichte der Zahlen. Campus Verlag, Frankfurt/ New York 1989, ISBN 3-593-34192-1 (französisch: Histoire Universelle des Chiffres. Übersetzt von Alexander von Platen).
Jürgen Schmidt: Basiswissen Mathematik. 2. Auflage. Springer, Berlin Heidelberg 2015, ISBN 978-3-662-43545-8.
Peter Pepper: Grundlagen der Informatik. Oldenbourg, München/ Wien 1992, ISBN 3-486-21153-6.
Dirk W. Hoffmann: Grundlagen der Technischen Informatik. 4. Auflage. Hanser, 2014, ISBN 978-3-446-44251-1, Zahlendarstellung und Codes, S. 59–88, doi:10.3139/9783446442481.
Hermann Maier: Didaktik der Zahldarstellung – Ein Arbeitsbuch zur Unterrichtsplanung. Schöningh, Paderborn 1992, ISBN 3-506-37487-7.

Einzelnachweise

Josef Stoer, Roland W. Freund, Ronald H. W. Hoppe, R. Bulirsch: Numerische Mathematik. 10. Auflage. Band 1. Springer, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-45389-5.
Vgl. Ifrah (1989), S. 47 ff.
Karl Menninger: Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl. 2. Auflage. Band 1. Vandenhoeck & Ruprecht, Göttingen 1958, ISBN 3-525-40701-7 (digitale-sammlungen.de). S. 64.
Menninger: Zahlwort und Ziffer. 1958, S. 65.
K. Döhmann: Über Inkonsequenzen und Anomalien in der sprachlichen Zahlendarstellung. In: Die Pyramide. Band 3, Nr. 11, 12. Innsbruck Dezember 1953, S. 233–235.
Friedhelm Padberg/ Rainer Dankwerts/ Martin Stein: Zahlbereiche. Spektrum Akademischer Verlag, Heidelberg/ Berlin/ Oxford 1995, ISBN 3-86025-394-8. S. 159 ff.
Ein Nachweis für die Verwendung des Wortes „Zahlenkreis“ in der Mathematik fehlt, in Timo Leuders: Erlebnis Arithmetik. Spektrum, Heidelberg 2012, ISBN 978-3-8274-2414-3, S. 145. wird stattdessen der Begriff „kreisförmiger Zahlenstrahl“ benutzt.
Ehrhard Behrends: Analysis Band 1. 6. Auflage. Springer, Wiesbaden 2015, ISBN 978-3-658-07122-6, doi:10.1007/978-3-658-07123-3. S. 52–58.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Josef Stoer, Roland W. Freund, Ronald H. W. Hoppe, R. Bulirsch: Numerische Mathematik. 10. Auflage. Band 1. Springer, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-45389-5.

[Ifrah-Zahlzeiche-Symbole-2] Vgl. Ifrah (1989), S. 47 ff.

[3] Karl Menninger: Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl. 2. Auflage. Band 1. Vandenhoeck & Ruprecht, Göttingen 1958, ISBN 3-525-40701-7 (digitale-sammlungen.de). S. 64.

[4] Menninger: Zahlwort und Ziffer. 1958, S. 65.

[Sprachliche_Inkonsequenz-5] K. Döhmann: Über Inkonsequenzen und Anomalien in der sprachlichen Zahlendarstellung. In: Die Pyramide. Band 3, Nr. 11, 12. Innsbruck Dezember 1953, S. 233–235.

[6] Friedhelm Padberg/ Rainer Dankwerts/ Martin Stein: Zahlbereiche. Spektrum Akademischer Verlag, Heidelberg/ Berlin/ Oxford 1995, ISBN 3-86025-394-8. S. 159 ff.

[7] Ein Nachweis für die Verwendung des Wortes „Zahlenkreis“ in der Mathematik fehlt, in Timo Leuders: Erlebnis Arithmetik. Spektrum, Heidelberg 2012, ISBN 978-3-8274-2414-3, S. 145. wird stattdessen der Begriff „kreisförmiger Zahlenstrahl“ benutzt.

[8] Ehrhard Behrends: Analysis Band 1. 6. Auflage. Springer, Wiesbaden 2015, ISBN 978-3-658-07122-6, doi:10.1007/978-3-658-07123-3. S. 52–58.