Pythagoreer
Als Pythagoreer (auch Pythagoräer, altgriechisch Πυθαγόρειοι Pythagóreioi oder Πυθαγορικοί Pythagorikoí) bezeichnet man im engeren Sinne die Angehörigen einer religiös-philosophischen, auch politisch aktiven Schule, die Pythagoras von Samos in den zwanziger Jahren des 6. Jahrhunderts v. Chr. in Süditalien gründete und die nach seinem Tod noch einige Jahrzehnte fortbestand. Im weiteren Sinn sind damit alle gemeint, die seither Ideen des Pythagoras oder ihm zugeschriebene Ideen aufgegriffen und zu einem wesentlichen Bestandteil ihres Weltbildes gemacht haben.

Wegen der verworrenen Quellenlage sind viele Einzelheiten der philosophischen Überzeugungen und politischen Ziele der Pythagoreer unklar, zahlreiche Fragen sind in der Forschung stark umstritten. Sicher ist, dass in einer Reihe von griechischen Städten Süditaliens Gemeinschaften von Pythagoreern bestanden, die sich als soziale und politische Reformbewegung betrachteten und mit Berufung auf die Lehren des Schulgründers massiv in die Politik eingriffen. Dabei kam es zu schweren, gewaltsamen Auseinandersetzungen, die im 5. Jahrhundert v. Chr. mit wechselndem Erfolg ausgetragen wurden und schließlich mit Niederlagen der Pythagoreer endeten. In den meisten Städten wurden die Pythagoreer getötet oder vertrieben.
Für die Pythagoreer charakteristisch ist die Überzeugung, dass der Kosmos eine nach bestimmten Zahlenverhältnissen aufgebaute harmonische Einheit bildet, deren einzelne Bestandteile ebenfalls harmonisch strukturiert sind oder, soweit es sich um menschliche Lebensverhältnisse handelt, harmonisch gestaltet werden sollten. Sie nahmen an, dass in allen Bereichen – in der Natur, im Staat, in der Familie und im einzelnen Menschen – dieselben zahlenmäßig ausdrückbaren Gesetzmäßigkeiten gelten, dass überall Ausgewogenheit und harmonischer Einklang anzustreben sind und dass die Kenntnis der maßgeblichen Zahlenverhältnisse eine weise, naturgemäße Lebensführung ermöglicht. Das Streben nach Eintracht beschränkten sie nicht auf die menschliche Gesellschaft, sondern dehnten es auf die Gesamtheit der Lebewesen aus, was sich in der Forderung nach Rücksichtnahme auf die Tierwelt zeigte.
Forschungsprobleme
Von Pythagoras sind keine authentischen Schriften überliefert, nur einige ihm zugeschriebene Verse sind möglicherweise echt. Schon in der Antike gab es unterschiedliche Meinungen darüber, welche der als pythagoreisch geltenden Lehren tatsächlich auf ihn zurückgehen. Die Unterscheidung zwischen frühpythagoreischem und späterem Gedankengut gehört bis heute zu den schwierigsten und umstrittensten Fragen der antiken Philosophiegeschichte. In der Forschung ist sogar strittig, ob es sich bei der Lehre des Pythagoras tatsächlich um Philosophie und um wissenschaftliche Bestrebungen handelte oder um eine rein mythisch-religiöse Kosmologie. Zu diesen Schwierigkeiten trägt das frühe Einsetzen einer üppigen Legendenbildung bei.
Die Schule des Pythagoras
Die politische Geschichte der Schule bis zu ihrem Untergang im 5. Jahrhundert v. Chr. ist in Umrissen bekannt. Hinsichtlich ihres Zwecks und ihrer Arbeitsweise und Organisation gehen die Meinungen der Historiker jedoch weit auseinander.
Politische Geschichte der Schule
Pythagoras stammte von der griechischen Insel Samos. Er emigrierte zwischen 532 und 529 v. Chr. in ein damals von Griechen besiedeltes Gebiet Süditaliens, wo er sich zunächst in Kroton (heute Crotone in Kalabrien) niederließ.[1] Dort gründete er die Schule, die von Anfang an neben den Studien auch politische Ziele verfolgte. Am Krieg zwischen Kroton und der ebenfalls griechischen Stadt Sybaris, der von Sybaris ausging und mit großer Brutalität ausgetragen wurde, nahmen die Pythagoreer aktiv teil. Der Befehlshaber des Heeres der Krotoniaten, der berühmte Athlet Milon, war Pythagoreer.[2]
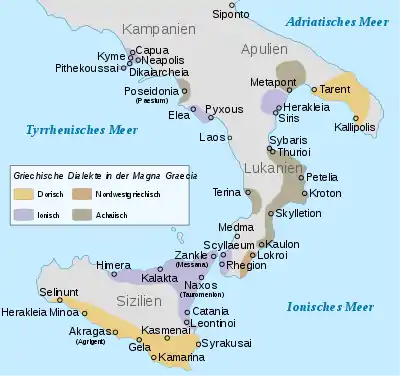
Nach dem Sieg über Sybaris, das erobert und geplündert wurde (510), wurden die Pythagoreer in heftige Auseinandersetzungen innerhalb der Bürgerschaft von Kroton verwickelt. Dabei ging es um die Verteilung des eroberten Landes und um eine Verfassungsänderung. Wegen dieser Unruhen verlegte Pythagoras seinen Wohnsitz nach Metapontion (heute Metaponto in der Basilikata). Dort setzte er seine Lehrtätigkeit fort, während in Kroton seine hart bedrängten Anhänger unterlagen und vorübergehend die Stadt verlassen mussten. Als Anführer der gegnerischen Partei trat ein vornehmer Bürger namens Kylon hervor (daher „kylonische Unruhen“), und auch ein Volksredner namens Ninon hetzte gegen die Pythagoreer. Berichte einzelner Quellen, wonach es damals bereits zu einer blutigen Verfolgung kam, beruhen aber anscheinend auf Verwechslung mit späteren Vorgängen.[3]
Da die Schule erhebliche Ausstrahlungskraft hatte, bildeten sich auch in anderen griechischen Städten Süditaliens Pythagoreergemeinschaften, die wohl auch dort in die Politik eingriffen. Eine institutionalisierte Herrschaft der Pythagoreer hat es aber weder in Kroton noch in Metapontion oder anderswo gegeben, sondern nur eine mehr oder weniger erfolgreiche Einflussnahme auf den jeweiligen Rat der Stadt und auf die Bürgerversammlung.[4] Mehrere Quellen berichten, dass der Pythagoreismus sich auch in der nichtgriechischen Bevölkerung verbreitete. Genannt werden u. a. die Stämme der Lukanier und Messapier.[5]
Pythagoras starb in den letzten Jahren des 6. Jahrhunderts oder im frühen 5. Jahrhundert.[6] Nach seinem Tod setzten seine Schüler ihre Aktivitäten in den Städten fort. Es bestand nun aber wohl keine zentrale Lenkung der Schule mehr, denn Pythagoras hatte anscheinend keinen Nachfolger als allgemein anerkanntes Schuloberhaupt.[7] Die Pythagoreer waren – gemäß ihrer insgesamt auf Harmonie und Stabilität ausgerichteten Weltanschauung – politisch konservativ. Dadurch wurden sie zu Verbündeten der traditionell in den Stadträten dominierenden Geschlechter. Sie stießen aber, wie das Beispiel Kylons zeigt, in den einflussreichen Familien auch auf Opposition. Ihre natürlichen Feinde waren überall die Agitatoren, die für einen Umsturz und für die Einführung der Demokratie eintraten und nur auf diesem Wege Macht erlangen konnten.[8]
Um die Mitte des 5. Jahrhunderts oder etwas später kamen in einer Reihe von Städten demokratisch gesinnte Volksredner an die Macht. Sie gingen, damaliger Sitte folgend, mit großer Härte gegen die Anhänger der unterlegenen Partei vor. Daher kam es zu blutigen Verfolgungen der Pythagoreer, die entweder getötet wurden oder aus den Städten fliehen mussten. Die politischen Wirren hielten anscheinend längere Zeit an. Dabei konnten die Pythagoreer sich zeitweilig wieder durchsetzen; schließlich unterlagen sie jedoch überall außer in Tarent, wo sie noch bis um die Mitte des 4. Jahrhunderts eine starke Stellung hatten. Viele von ihnen emigrierten nach Griechenland. Die Schule hörte als Organisation zu bestehen auf.[9]
Der Unterricht und sein Zweck
Die Pythagoreer zerfielen laut einigen Quellenberichten in zwei Gruppen oder Richtungen, die „Mathematiker“ und die „Akusmatiker“. „Mathematiker“ waren diejenigen, welche sich mit „Mathemata“ befassten, das heißt mit schriftlich festgehaltenen Lerngegenständen und Empirie (auch, aber nicht nur Mathematik im heutigen Wortsinn).[10] Dies kann als eine frühe Form von mathematisch-naturwissenschaftlicher Forschung betrachtet werden. Akusmatiker wurden Pythagoreer genannt, die sich auf „Akusmata“ (Gehörtes) beriefen, also auf die nur mündlich mitgeteilten Lehren des Pythagoras; dabei ging es hauptsächlich um Verhaltensregeln und das religiöse Weltbild.
Unklar ist, ob schon Pythagoras seine Schüler gemäß ihren Neigungen und Fähigkeiten in zwei Gruppen mit verschiedenen Aufgaben aufteilte oder die Abgrenzung zwischen den beiden Richtungen erst nach seinem Tod deutlich wurde. Jedenfalls kam es nach einem Bericht, den manche Forscher auf Aristoteles zurückführen,[11] zu einem unbekannten Zeitpunkt nach dem Tod des Schulgründers zu einer Spaltung zwischen den zwei Richtungen. Dabei nahm jede von ihnen für sich in Anspruch, die authentische Tradition des Pythagoras fortzusetzen.[12]
Der völlig verschiedenartige Charakter dieser beiden Richtungen gibt bis heute Rätsel auf. So ist unklar, welche der beiden Gruppen älter, welche größer und welche für den Pythagoreismus wichtiger war, welche den Kern der Schule ausmachte und damit als fortgeschrittener und höherrangig galt. Darüber gehen die Ansichten in der Forschung weit auseinander.
Manche Gelehrte (besonders Walter Burkert) meinen, dass zu Lebzeiten des Pythagoras alle Pythagoreer Akusmatiker waren und dass die griechische Wissenschaft außerhalb des Pythagoreismus entstanden ist. Demnach waren die „Mathematiker“ einzelne Pythagoreer, die sich erst nach dem Tod des Schulgründers mit wissenschaftlichen Anliegen zu befassen begannen; ihr Wirken fiel größtenteils in die Zeit nach dem Untergang der Schule. Diese „Mathematiker“ waren aber diejenigen Repräsentanten des Pythagoreismus, mit denen sich Platon im 4. Jahrhundert auseinandersetzte. Sie prägten das später (und bis heute) in der Öffentlichkeit vorherrschende, nach Burkerts Ansicht falsche Bild vom anfänglichen Pythagoreismus, indem sie ihn als eine Pflanzstätte wissenschaftlicher Forschung erscheinen ließen. Hinzu kam, dass schon die Schüler Platons und des Aristoteles platonische Gedanken für pythagoreisch hielten. In Wirklichkeit war die Schule nach Burkerts Deutung ein Bund mit religiösen und politischen Zielen, der seine esoterischen Lehren geheim hielt und kein Interesse an Wissenschaft hatte. Burkert vergleicht die Pythagoreergemeinschaft mit den Mysterienkulten.
Der Hauptvertreter der gegenteiligen Auffassung ist gegenwärtig Leonid Zhmud. Sie besagt, es habe weder eine Geheimlehre der frühen Pythagoreer noch eine für alle verbindliche religiöse Doktrin gegeben. Die Schule sei eine „Hetairie“ gewesen, ein lockerer Zusammenschluss autonom forschender Personen. Diese hätten sich gemeinschaftlich – aber ohne Fixierung auf vorgegebene Dogmen – ihren wissenschaftlichen und philosophischen Studien gewidmet. Außerdem seien sie durch bestimmte politische Ziele verbunden gewesen. Die Berichte über die Akusmatiker seien späte Erfindungen. Die Akusmata – ursprünglich „Symbola“ genannt – seien nur Sprüche und nicht konkrete, verbindliche Regeln für den Alltag gewesen. Sie seien zwar sehr alt, wie auch Burkert meint, aber großenteils nicht pythagoreischen Ursprungs. Vielmehr seien es teils Weisheitssprüche unbestimmter Herkunft, teils handle es sich um uralten Volksaberglauben, der in Pythagoreerkreisen in symbolischem Sinn umgedeutet wurde.
Burkert bemerkt: „Die modernen Kontroversen um Pythagoras und den Pythagoreismus sind im Grunde nur die Fortsetzung des alten Streits zwischen ‚Akusmatikern‘ und ‚Mathematikern‘.“[13]
Andere Gelehrte wie B. L. van der Waerden vertreten eine Mittelposition. Sie weisen weder der einen noch der anderen Gruppe die Priorität und alleinige Authentizität zu, sondern meinen, die Unterscheidung zwischen Mathematikern und Akusmatikern gehe auf unterschiedliche Bestrebungen zurück, die schon zu Pythagoras’ Lebzeiten in der Schule bestanden. Nach dem Tod des Schulgründers habe sich daraus ein Gegensatz entwickelt, der zur Spaltung der Schule führte.
Späte Quellen schildern die Pythagoreer – gemeint sind offenbar Akusmatiker – als eine verschworene Gemeinschaft von Jüngern, die ihren Meister als göttliches oder jedenfalls übermenschliches Wesen verehrten und blind an seine Unfehlbarkeit glaubten. Dieser Glaube soll dazu geführt haben, dass sie jede Frage durch Berufung auf eine (angebliche) mündliche Äußerung des Pythagoras entschieden. Allein der „Autoritätsbeweis“ durch die Versicherung „Er selbst [Pythagoras] hat es gesagt“ habe bei ihnen gegolten.[14] In diesen Zusammenhang gehören auch Berichte, wonach Pythagoras Bewerber, die in seine Schule eintreten wollten, zunächst physiognomisch prüfte und ihnen dann eine lange (nach manchen Angaben fünfjährige) Schweigezeit auferlegte, nach deren erfolgreicher Absolvierung sie in die Gemeinschaft aufgenommen wurden.[15]
Pythagoreer der Frühzeit
Der prominenteste unter den forschenden Pythagoreern der Frühzeit war der Mathematiker und Musiktheoretiker Hippasos von Metapont. Er soll Klangexperimente durchgeführt haben, um das Verhältnis der Konsonanzen zu messbaren physikalischen Größen zu bestimmen. Bekannt ist er vor allem durch die früher herrschende Ansicht, er habe eine „Grundlagenkrise“ des Pythagoreismus ausgelöst, indem er die Inkommensurabilität entdeckte und damit die Behauptung widerlegte, alle Phänomene seien als Erscheinungsformen ganzzahliger Zahlverhältnisse erklärbar. Angeblich schlossen die Pythagoreer Hippasos daraufhin aus und betrachteten seinen Tod durch Ertrinken im Meer als göttliche Strafe für den „Geheimnisverrat“. Die Entdeckung der Inkommensurabilität mag eine historische Tatsache sein, aber die Vermutung, dies habe zu einer Grundlagenkrise geführt, wird in der neueren Forschung abgelehnt.[16]
Zu den frühen Pythagoreern gehörten ferner:
- Milon von Kroton, einer der berühmtesten antiken Athleten.[17] Als einziger siegte er sechsmal in Olympia. Er war der siegreiche Heerführer Krotons im Krieg gegen Sybaris (510). Milon soll eine Tochter des Pythagoras namens Myia geheiratet haben.
- Demokedes von Kroton, der nach dem Urteil Herodots der beste Arzt seiner Zeit war. Er war Schwiegersohn Milons von Kroton und beteiligte sich auf der pythagoreischen Seite an den politischen Kämpfen in seiner Heimatstadt. Schon sein Vater, der Arzt Kalliphon, soll von Pythagoras beeinflusst gewesen sein.[18]
- möglicherweise auch der berühmte Naturphilosoph Alkmaion von Kroton, der die Gesundheit als harmonisches Gleichgewicht gegensätzlicher Kräfte im Körper auffasste. Ob er auch als Arzt praktizierte, ist umstritten.[19]
In der Frühzeit sollen auch Frauen in der Bewegung aktiv gewesen sein. Insbesondere wird in den Quellen oft der Name von Pythagoras’ Gattin Theano genannt. Ihr wurden später zahlreiche Aussprüche und Schriften zugeschrieben, die vor allem von Tugend und Frömmigkeit handelten, sowie sieben Briefe, die erhalten sind.[20]
Der Philosoph Parmenides soll Schüler eines Pythagoreers namens Ameinias gewesen sein; pythagoreischer Einfluss auf ihn wird von der heutigen Forschung angenommen, das Ausmaß ist aber unklar.[21] Der Philosoph Empedokles, der Pythagoras bewunderte, war zwar kein Pythagoreer im engeren Sinne, stand aber der pythagoreischen Gedankenwelt sehr nahe.
Lehren und Legenden
Trotz der ungeheueren persönlichen Autorität des Pythagoras war der frühe ebenso wie auch der spätere Pythagoreismus kein verbindlich fixiertes, in sich geschlossenes und detailliert ausgearbeitetes dogmatisches Lehrgebäude. Eher handelte es sich um eine bestimmte Art der Weltbetrachtung, die für unterschiedliche Ansätze Spielraum ließ. Alle Pythagoreer teilten die Grundüberzeugung, die gesamte erkennbare Welt sei eine auf der Basis bestimmter Zahlen und Zahlenverhältnisse aufgebaute, prinzipiell harmonisch gestaltete Einheit. Diese Gesetzmäßigkeit bestimme alle Bereiche der Wirklichkeit gleichermaßen. Die Kenntnis der maßgeblichen Zahlenverhältnisse betrachteten sie daher als den Schlüssel zum Verständnis von allem und als Voraussetzung für eine gute, naturgemäße Lebensführung. Ihr Ziel war es, die unterschiedlichen und gegensätzlichen Kräfte durch Ausgewogenheit zu einem harmonischen Einklang zu bringen, sowohl im menschlichen Körper als auch in der Familie und im Staat. Dabei wollten sie das, was sie als Maß, Ordnung und Harmonie zu erkennen meinten, überall in der Natur finden und in ihrem eigenen Leben wahren. Sie gingen also von einer ganzheitlichen Deutung des Kosmos aus. Das, was in ihm in Unordnung geraten war, wollten sie in die natürliche Ordnung zurückbringen. Im Sinne dieses Weltbildes hielten sie alle beseelten Wesen für miteinander verwandt und leiteten daraus ein Gebot der Rücksichtnahme ab. Hinsichtlich der Einzelheiten gingen ihre Meinungen aber oft weit auseinander.
Seelenlehre
Die Lehre von der Unsterblichkeit der Seele gehört zum ältesten Bestand der frühpythagoreischen Philosophie. Sie ist eine der wichtigsten Gemeinsamkeiten von Pythagoreismus und Platonismus, die sich im Lauf ihrer Entwicklung gegenseitig beeinflussten und bei manchen Philosophen miteinander verschmolzen. Die Pythagoreer waren ebenso wie die Platoniker von der Seelenwanderung überzeugt. Dabei nahmen sie keinen Wesensunterschied zwischen menschlichen und tierischen Seelen an. Diese Idee setzte die Unsterblichkeit der Seele voraus. Da jedoch die Pythagoreer in den harmonischen Zahlenverhältnissen das Fundament der Weltordnung sahen, gab es bei ihnen auch die Vorstellung, dass die Seele eine Harmonie sei, nämlich das harmonische Gleichgewicht der den Körper bestimmenden Kräfte.[22] Das ist mit der Unsterblichkeitsidee schwer zu vereinbaren. In diesem Widerspruch zeigt sich die Unfertigkeit des in Entwicklung begriffenen pythagoreischen Philosophierens. Platon setzte sich in seinem Dialog Phaidon mit der Deutung der Seele als Harmonie auseinander und bemühte sich sie zu widerlegen.
Ein weiterer Bereich, in dem innerhalb der pythagoreischen Bewegung offenbar disparate Ideen vertreten und nicht zu einem stimmigen Ganzen verbunden wurden, war die Frage nach der Bestimmung und Zukunft der Seele.[23] Ein wesentlicher, allerdings für die sehr quellenarme Frühzeit nicht eindeutig bezeugter Bestandteil des Pythagoreismus war die religiöse Überzeugung, dass die menschliche Seele göttlicher Herkunft und Natur sei. Daraus folgte (wie bei den Orphikern und den Platonikern), dass es die Aufgabe und Bestimmung der Seele sei, aus dem Diesseits in ihre jenseitige Heimat zurückzukehren. Darauf sollte sie sich durch Schulung und rechte Lebensführung vorbereiten. Ihr wurde zugetraut, ihre göttlichen Fähigkeiten und Möglichkeiten zurückzuerlangen.[24] Der Umstand, dass Pythagoras von vielen seiner Anhänger als gottähnliches Wesen betrachtet wurde, zeigt, dass ein solches Ziel grundsätzlich erreichbar schien. Mit diesem Erlösungsstreben schwer vereinbar war jedoch ein anderes Konzept, welches von einem ewigen, unabänderlichen Kreislauf des Weltgeschehens ausging. Die Annahme, dass ein einheitlicher Kosmos immer und überall von den gleichen mathematischen Gegebenheiten bestimmt sei, und die zyklische Natur der gleichmäßigen Bewegungen der Himmelskörper führten dazu, auch das Schicksal der Menschheit als vorbestimmt und zyklisch aufzufassen. Daher herrschte zumindest bei einem Teil der Pythagoreer ein astrologischer Fatalismus, also die Vorstellung von der zwangsläufigen ewigen Wiederkunft aller irdischen Verhältnisse entsprechend den Gestirnbewegungen. Dieser Idee zufolge beginnt die Weltgeschichte von neuem als exakte Wiederholung, sobald alle Planeten nach Ablauf einer langen kosmischen Periode, des „Großen Jahres“, ihre Ausgangsstellung wieder erreicht haben.[25]
Als religiöse Erlösungslehre präsentierte sich der Pythagoreismus insbesondere in einem sehr populären antiken Gedicht eines unbekannten Autors, den „Goldenen Versen“. Dort wird dem Menschen, der sich an die philosophischen Lebensregeln hält und zur Erkenntnis der Weltgesetze vorgedrungen ist, in Aussicht gestellt, dass seine Seele dem Leiden und der Sterblichkeit entrinnen und in die Daseinsweise unsterblicher Götter überwechseln könne.[26] Dies hatte schon im 5. Jahrhundert Empedokles als Ziel formuliert.
Ernährung und Kleidung
Ebenso wie viele andere philosophische Richtungen traten die Pythagoreer für Beherrschung der Begierden und damit auch für eine einfache Lebensweise und frugale Ernährung ein. Dass sie jeden Luxus – insbesondere den Kleiderluxus – verwarfen, ergab sich aus ihrer allgemeinen Forderung, das rechte Maß zu wahren und so die Harmonie zu verwirklichen.[27]
Ein Kernbestandteil des ursprünglichen Pythagoreismus war der Vegetarismus. Er wurde als „Enthaltung vom Beseelten“ bezeichnet.[28] Diese Bezeichnung weist auf die ethische und religiöse Wurzel des pythagoreischen Vegetarismus hin. Er hing mit der Überzeugung zusammen, dass die Seelen der Menschen und diejenigen der Tiere nicht essentiell verschieden seien und man den Tieren somit Rücksichtnahme schulde. Verschiedene Legenden, nach denen Pythagoras sich Tieren verständlich machen konnte, zeugen von einer besonderen Nähe der Pythagoreer zur Tierwelt.[29] Daher wurden neben der Fleischnahrung auch die Tieropfer verworfen. Damit waren aber soziale Probleme verbunden, denn die Teilnahme an den traditionellen Opfern und den anschließenden Opfermahlzeiten gehörte zu den wichtigsten gemeinschaftsstiftenden Bräuchen, und die politisch aktiven Pythagoreer mussten auf ihr Ansehen in der Bürgerschaft Wert legen. Daher gab es anscheinend kein für alle verbindliches Gebot, und nur ein Teil der Pythagoreer lebte vegetarisch.[30]
Ein strenges Tabu richtete sich gegen den Verzehr von Bohnen. Der ursprüngliche Grund des Bohnenverbots war schon in der Antike unbekannt, es wurde darüber gerätselt. Gelegentlich wurde ein gesundheitlicher Grund angedeutet, aber meist ging man davon aus, dass es ein religiöses Tabu war. Es wurde sogar angenommen, das Verbot sei so umfassend gewesen, dass es auch bloße Berührung einer Bohnenpflanze absolut untersagte. Daher entstanden Legenden, wonach vor Verfolgern fliehende Pythagoreer (bzw. Pythagoras selbst) eher den Tod in Kauf nahmen, als ein Bohnenfeld zu durchqueren. Der tatsächliche Grund für das Bohnentabu ist bis heute nicht geklärt. Die Möglichkeit eines Zusammenhangs mit dem Favismus, einer erblichen Enzymkrankheit, bei welcher der Genuss von Ackerbohnen (Vicia faba) gesundheitsgefährlich ist, wurde mehrfach als Erklärung erwogen. Diese Hypothese findet in den Quellen keine konkrete Stütze und ist daher spekulativ.[31]
Freundschaftsideal
Eine wichtige Rolle spielte im Pythagoreismus das Konzept der Freundschaft (philía). Dieser Begriff wurde gegenüber seiner normalen Bedeutung stark ausgeweitet. Da die Pythagoreer den Kosmos als Einheit von zusammengehörigen und harmonisch zusammenwirkenden Bestandteilen auffassten, gingen sie von einer naturgegebenen Freundschaft sämtlicher Lebewesen (einschließlich der Götter) untereinander aus. Dieses Ideal universaler Freundschaft und Harmonie in der Welt erinnert an den Mythos vom paradiesischen Goldenen Zeitalter.[32] Das Ziel war, die so verstandene Verbundenheit aller zu erkennen und im eigenen Leben umzusetzen. Damit war aber – wie die Beteiligung am Krieg gegen Sybaris schon zu Lebzeiten des Pythagoras zeigt – kein absoluter Gewaltverzicht im Sinne des Pazifismus verbunden.
Insbesondere praktizierten die Pythagoreer die Freundschaft untereinander. Manche von ihnen verstanden darunter eine unbedingte Loyalität nicht nur zu ihren persönlichen Freunden, sondern zu jedem Pythagoreer. Über die Freundestreue sind einige Anekdoten überliefert. Die berühmteste ist die Geschichte von Damon und Phintias, die von Friedrich Schiller für seine Ballade Die Bürgschaft verwertet wurde. Es wird erzählt, dass der Pythagoreer Phintias wegen eines Komplotts gegen den Tyrannen Dionysios zum Tode verurteilt wurde, aber die Erlaubnis erhielt, vor der Hinrichtung seine persönlichen Angelegenheiten in Freiheit zu regeln, da sich sein Freund Damon als Geisel für seine Rückkehr verbürgte. Phintias kehrte rechtzeitig zurück; anderenfalls wäre Damon an seiner Stelle hingerichtet worden. Dies beeindruckte den Tyrannen stark, worauf er Phintias begnadigte und selbst vergeblich um Aufnahme in den Freundschaftsbund bat. Nach einer Version hatte Dionysios den ganzen Vorfall nur zum Schein arrangiert, um die legendäre Treue der Pythagoreer auf die Probe zu stellen, nach einer anderen Version handelte es sich um eine wirkliche Verschwörung.[33]
Bekannt war in der Antike der Grundsatz der Pythagoreer, dass der Besitz der Freunde gemeinsam sei (koiná ta tōn phílōn). Dies ist aber nicht im Sinne einer „kommunistischen“ Gütergemeinschaft zu verstehen; eine solche wurde – wenn überhaupt – nur von wenigen praktiziert. Gemeint war, dass die Pythagoreer einander in materiellen Notlagen spontan und großzügig unterstützten.[34]
Mathematik und Zahlensymbolik
Zahlen und Zahlenverhältnisse haben in der pythagoreischen Lehre von Anfang an eine zentrale Rolle gespielt. Dies ist ein Merkmal, das den Pythagoreismus von anderen Ansätzen unterscheidet. Ob das aber bedeutet, dass Pythagoras schon Mathematik getrieben hat, ist strittig. Manche Forscher (insbesondere Walter Burkert) haben die Ansicht vertreten, er habe sich nur mit Zahlensymbolik befasst, wissenschaftliches Denken sei ihm fremd gewesen, und erst um die Mitte des 5. Jahrhunderts habe sich Hippasos als erster Pythagoreer mathematischen Studien zugewandt. Die Gegenposition von Leonid Zhmud lautet, die frühen Pythagoreer seien Mathematiker gewesen und die Zahlenspekulation sei erst spät hinzugekommen und nur von vereinzelten Pythagoreern betrieben worden.
Der Grundgedanke der Zahlenspekulation wird oft in dem Kernsatz „Alles ist Zahl“ zusammengefasst. In damaliger Ausdrucksweise besagt das, dass die Zahl für die Pythagoreer die archē, das konstituierende Urprinzip der Welt gewesen sei. Damit fiele der Zahl diejenige Rolle zu, die Thales dem Wasser und Anaximenes der Luft zugewiesen hatte. Diese Auffassung ist aber im frühen Pythagoreismus nicht belegt. Aristoteles schreibt sie „den Pythagoreern“ zu, ohne Namen zu nennen. Er kritisiert sie und unterstellt dabei, die Pythagoreer hätten unter den Zahlen etwas Stoffliches verstanden.[35]
In der zweiten Hälfte des 5. Jahrhunderts schrieb der Pythagoreer Philolaos, alles für uns Erkennbare sei notwendigerweise mit einer Zahl verknüpft, denn das sei eine Voraussetzung für gedankliches Erfassen. Seine Feststellung bezieht sich aber nur auf den menschlichen Erkenntnisprozess. Sie besagt nicht im Sinne einer Ontologie der Zahl, dass alle Dinge aus Zahlen bestehen oder hervorgehen. Die Auffassung, dass die Zahlen selbst die Dinge seien, wird oft als typisch pythagoreisch bezeichnet. Dies ist jedoch nur Aristoteles’ möglicherweise irriges Verständnis der pythagoreischen Lehre. Das für Philolaos Wesentliche war der Unterschied zwischen dem nach Zahl, Größe und Form Begrenzten und dem Unbegrenzten, das er für prinzipiell unerforschbar hielt, und das Zusammenspiel dieser beiden Faktoren.[36]
Ausgangspunkt der konkreten Zahlenspekulation war der Gegensatz von geraden und ungeraden Zahlen, wobei die ungeraden als begrenzt (und damit höherrangig) und – wie im chinesischen Yin und Yang – als männlich bezeichnet wurden und die geraden als unbegrenzt und weiblich. Die als Prinzip der Einheit aufgefasste Eins galt als der Ursprung, aus dem alle Zahlen hervorgehen (und infolgedessen die ganze Natur); so gesehen war sie selbst eigentlich keine Zahl, sondern stand jenseits der Zahlenwelt, obwohl sie rechnerisch als Zahl wie alle anderen erscheint. So konnte die Eins paradoxerweise als gerade und ungerade zugleich bezeichnet werden, was rechnerisch nicht zutrifft. Die Zahlen stellte man mit Zählsteinen dar, und mit den ebenen geometrischen Figuren, die mit solchen Steinen gelegt werden können (beispielsweise einem gleichseitigen Dreieck), wurden die den Zahlen zugewiesenen Eigenschaften demonstriert. Große Bedeutung legte man dabei der Tetraktys („Vierheit“) bei, der Gesamtheit der Zahlen 1, 2, 3 und 4, deren Summe die 10 ergibt, die bei Griechen und „Barbaren“ (Nichtgriechen) gleichermaßen als Grundzahl des Dezimalsystems diente. Die Tetraktys und die „vollkommene“ Zehn betrachtete man als für die Weltordnung grundlegend.
Einzelne mathematische Erkenntnisse wurden in der Antike – zu Recht oder zu Unrecht – den Pythagoreern oder einem bestimmten Pythagoreer zugeschrieben. Pythagoras soll einen Beweis für den nach ihm benannten Satz des Pythagoras über das rechtwinklige Dreieck gefunden haben. Hippasos von Metapont schrieb man die Konstruktion des einer Kugel einbeschriebenen Dodekaeders und die Entdeckung der Inkommensurabilität zu. Eine nicht genau bekannte Rolle spielten Pythagoreer bei der Entwicklung der Lehre von den drei Mitteln (arithmetisches, geometrisches und harmonisches Mittel). Ferner sollen sie unter anderem den Satz über die Winkelsumme im Dreieck bewiesen haben. Womöglich stammen große Teile von Euklids Elementen – sowohl der arithmetischen als auch der geometrischen Bücher – aus verlorener pythagoreischer Literatur; dazu gehörte die Theorie der Flächenanlegung.[37]
Kosmologie und Astronomie
In der Astronomie vertraten die Pythagoreer keinen einheitlichen Standpunkt. Das älteste Modell, das wir kennen, ist dasjenige des Philolaos aus der zweiten Hälfte des 5. Jahrhunderts. Es nimmt ein Zentralfeuer an, das den Mittelpunkt des Universums bildet und um das die Himmelskörper einschließlich der Erde kreisen. Für uns ist es unsichtbar, da die bewohnten Gegenden der Erde auf der ihm stets abgewandten Seite liegen. Um das Zentralfeuer kreist auf der innersten Bahn die Gegenerde, die für uns ebenfalls unsichtbar ist, da sie vom Zentralfeuer verdeckt wird. Darauf folgen (von innen nach außen) die Erdbahn und die Bahnen von Mond, Sonne und fünf Planeten (Merkur, Venus, Mars, Jupiter und Saturn). Umschlossen ist das Ganze von einer kugelförmigen Schale, auf der sich die Fixsterne befinden.[38] Aristoteles kritisierte dieses System, da es nicht von den Erscheinungen, sondern von vorgefassten Ansichten ausgehe; die Gegenerde sei nur eingeführt worden, um die Zahl der bewegten Körper am Himmel auf zehn zu bringen, da diese Zahl als vollkommene galt.
Aristoteles erwähnt, dass „einige“ Pythagoreer einen Kometen zu den Planeten zählten. Das widerspricht der Zehnzahl bei Philolaos. Auch über die Milchstraße hatten die Pythagoreer keine einheitliche Meinung. Daraus ist zu ersehen, dass die frühen Pythagoreer kein gemeinsames, für alle verbindliches Kosmosmodell hatten.[39] Manche Forscher nehmen an, dass es vor Philolaos ein völlig anderes, nämlich geozentrisches pythagoreisches Modell gab. Es sah vor, dass sich die kugelförmige Erde im Zentrum des Kosmos befindet und vom Mond, der Sonne und den damals bekannten fünf Planeten umkreist wird.[40]
Zu den wichtigsten Annahmen der Pythagoreer gehörte die Idee der Sphärenharmonie oder – wie die Bezeichnung in den ältesten Quellen lautet – „Himmelsharmonie“. Man ging davon aus, dass bei der Kreisbewegung der Himmelskörper ebenso wie bei Bewegungen irdischer Objekte Geräusche entstehen. Wegen der Gleichförmigkeit der Bewegung konnte dies für jeden Himmelskörper immer nur ein konstanter Ton sein. Die Gesamtheit dieser Töne, deren Höhe von den unterschiedlichen Geschwindigkeiten und den Abständen der Himmelskörper abhing, sollte einen kosmischen Klang ergeben. Diesen betrachtete man als für uns unhörbar, da er ununterbrochen erklinge und uns nur durch sein Gegenteil, durch einen Gegensatz zwischen Klang und Stille zu Bewusstsein käme. Allerdings soll Pythagoras laut einer Legende als einziger Mensch imstande gewesen sein, die Himmelsharmonie zu hören.[41]
Da die Töne der Himmelskörper nur als gleichzeitig, nicht als nacheinander erklingend gedacht werden konnten, musste als Ergebnis ihres Zusammenklingens ein ebenfalls stets unveränderter Klang angenommen werden. Daher ist der populäre Begriff „Sphärenmusik“ sicher unpassend. Dass der Zusammenklang harmonisch ist, ergibt sich in diesem Modell aus der Annahme, dass die Entfernungen der kreisenden Himmelskörper vom Zentrum und ihre bei größerer Entfernung entsprechend höheren Geschwindigkeiten eine bestimmte arithmetische Proportion aufweisen, die dies ermöglicht.[42]
Musik
Die Musik war derjenige Bereich, in dem die Grundidee einer auf Zahlenverhältnissen beruhenden Harmonie am einfachsten demonstrierbar war. Den musikalischen Gesetzmäßigkeiten galt die besondere Aufmerksamkeit der Pythagoreer. Auf diesem Gebiet haben sie offenbar auch experimentiert. Pythagoras wurde in der Antike allgemein als Begründer der mathematischen Analyse der Musik angesehen. Platon bezeichnete die Pythagoreer als Urheber der musikalischen Zahlenlehre, sein Schüler Xenokrates schrieb die entscheidende Entdeckung Pythagoras selbst zu. Dabei ging es um die Darstellung der harmonischen Intervalle durch einfache Zahlenverhältnisse. Das konnte durch Streckenmessung veranschaulicht werden, da die Tonhöhe von der Länge einer schwingenden Saite abhängt. Für solche Versuche eignete sich das Monochord mit verstellbarem Steg. Einen anderen, ebenfalls tauglichen Weg zur Quantifizierung fand Hippasos, der die Töne bronzener Scheiben von unterschiedlicher Dicke bei gleichem Durchmesser untersuchte.
Sicher unhistorisch ist allerdings die Legende von Pythagoras in der Schmiede, der zufolge Pythagoras zufällig an einer Schmiede vorbeiging und, als er die unterschiedlichen Klänge der verschieden schweren Hämmer hörte, sich von dieser Beobachtung dazu anregen ließ, mit an Saiten aufgehängten Metallgewichten zu experimentieren.[43]
Platon, der eine rein spekulative, aus allgemeinen Prinzipien abgeleitete Musiktheorie forderte und die Sinneserfahrung durch das Gehör für unzureichend hielt, kritisierte die Pythagoreer wegen ihres empirischen Vorgehens.[44]
Die Musik eignete sich zur Abstützung der These einer universalen Harmonie und der Verflochtenheit aller Teile des Kosmos. Durch die Idee der klingenden Himmelsharmonie war sie mit der Astronomie verbunden, durch die Messbarkeit der Tonhöhen mit der Mathematik, durch ihre Wirkung auf das Gemüt mit der Seelenkunde, der ethischen Erziehung und der Heilkunst. Die Pythagoreer befassten sich mit den unterschiedlichen Wirkungen verschiedener Instrumente und Tonarten auf das menschliche Gemüt. Den Legenden zufolge setzte Pythagoras ausgewählte Musik gezielt zur Beeinflussung unerwünschter Affekte und zu Heilzwecken ein, betrieb also eine Art Musiktherapie.[45]
Entwicklung nach den antipythagoreischen Unruhen
Von den Pythagoreern der zweiten Hälfte des 5. Jahrhunderts scheint der Naturphilosoph Philolaos einer der prominentesten gewesen zu sein. Er gehörte anscheinend zu denjenigen, die wegen der politischen Verfolgung in Italien nach Griechenland gingen. Jedenfalls lehrte er zumindest zeitweilig in Theben. Seine Kosmologie mit der Annahme eines Zentralfeuers in der Mitte des Universums unterschied sich stark von der zuvor dominierenden. Den Mond hielt er für bewohnt, die Sonne für glasartig (also kein eigenes Licht ausstrahlend, sondern fremdes Licht wie eine Linse sammelnd). Seine Ansichten sind nur aus Fragmenten seines Buchs bekannt, deren Echtheit zum Teil umstritten ist.[46]
Im 4. Jahrhundert v. Chr. war der bedeutendste Pythagoreer der mit Platon befreundete Archytas von Tarent. Er war sowohl ein erfolgreicher Staatsmann und Heerführer seiner Heimatstadt als auch Philosoph, Mathematiker, Physiker, Musiktheoretiker und ein hervorragender Ingenieur. Das pythagoreische Konzept einer mathematisch fassbaren Harmonie wandte er auf die Politik an, indem er für einen kalkulierten Ausgleich zwischen den sozialen Schichten eintrat. Die Eintracht der Bürger führte er auf eine angemessene, von allen als gerecht empfundene Besitzverteilung zurück.
Platon befasste sich intensiv mit der pythagoreischen Philosophie. Umstritten ist die Frage, inwieweit die Ansichten des Philolaos und des Archytas sein Bild von ihr prägten. Nach seinem Tod dauerte in der Platonischen Akademie das Interesse am Pythagoreismus an, und unter den Platonikern bestand die Neigung, Anregungen aus dieser Tradition aufzunehmen und Platon in entsprechendem Sinne zu deuten.[47]
Aristoteles verfasste eine Schrift über die Pythagoreer, von der nur Fragmente erhalten geblieben sind, und setzte sich auch sonst kritisch mit dem Pythagoreismus auseinander. Unter anderem argumentierte er gegen die Himmelsharmonie (Sphärenharmonie).
Im 4. Jahrhundert lebten in Griechenland zahlreiche aus Italien geflüchtete Anhänger des Pythagoras. Man unterschied nun zwischen „Pythagoreern“ und „Pythagoristen“ (von Πυθαγοριστής Pythagoristḗs „die pythagoreische Lebensweise Befolgender“). Die letzteren waren ein beliebtes Ziel des Spotts der Komödiendichter, da sie bettelten und asketisch lebten. Besonders ihre äußerst genügsame Ernährungsweise wurde in Komödien aufs Korn genommen. Sie wurden als schmutzige Sonderlinge dargestellt.[48]
Daneben gab es aber unter den aus Italien emigrierten Pythagoreern auch Gelehrte, die sich Respekt zu verschaffen wussten. Zu ihnen gehörte Lysis. Er wurde in Theben Lehrer des später berühmten Staatsmanns und Feldherrn Epameinondas; auf diesem Weg hat möglicherweise der Pythagoreismus ein letztes Mal auf die Politik Einfluss genommen.[49]
Zu den im späten 5. und im 4. Jahrhundert tätigen Pythagoreern gehörten ferner:
- Damon und Phintias aus Syrakus, deren berühmte Freundschaft für die Nachwelt vorbildlich wurde
- Diodoros von Aspendos, der besonders den pythagoreischen Vegetarismus vertrat und durch sein Auftreten als barfüßiger, langhaariger Asket Aufsehen erregte
- Echekrates von Phleius, ein Schüler des Philolaos, der in Platons Dialog Phaidon als Gesprächspartner auftritt
- Ekphantos, der ein geozentrisches Weltbild vertrat, wobei er eine Achsendrehung der Erde von West nach Ost annahm. In der Erkenntnistheorie war er Subjektivist.
- Eurytos, ein Schüler des Philolaos, der die pythagoreische Zahlenlehre auf Tiere und Pflanzen anwendete
- Hiketas von Syrakus, der die täglichen Veränderungen am Himmel auf die Achsendrehung der Erde zurückführte
- Kleinias von Tarent, der wegen seiner Freundestreue gerühmt wurde; er soll Platon von dem Vorhaben abgebracht haben, alle erreichbaren Bücher Demokrits zu verbrennen
- Lykon von Iasos, der für eine maßvolle Lebensweise nach dem Vorbild des Pythagoras eintrat und Aristoteles wegen dessen aufwendigen Lebensstils kritisierte
- Xenophilos von der Chalkidike, ein Schüler des Philolaos und Lehrer des Philosophen Aristoxenos
Neupythagoreismus
Bei den Römern stand Pythagoras in hohem Ansehen. Er wurde als Lehrer des zweiten Königs von Rom, Numa Pompilius, bezeichnet, was allerdings chronologisch unmöglich ist. Im 1. Jahrhundert v. Chr. bemühte sich anscheinend der mit Cicero befreundete Gelehrte und Senator Nigidius Figulus um eine Erneuerung des Pythagoreismus. Da eine kontinuierliche Tradition nicht mehr bestand,[50] war dies ein Neuanfang. Daher pflegt man Nigidius als den ersten Neupythagoreer zu bezeichnen; allerdings ist nicht klar, ob seine tatsächlichen Ansichten und Aktivitäten diese Bezeichnung rechtfertigen. Der Neupythagoreismus dauerte bis in die Spätantike fort, doch gab es keinen kontinuierlichen Schulbetrieb, sondern nur einzelne pythagoreisch gesinnte Philosophen und Gelehrte. Es handelte sich beim Neupythagoreismus nicht um eine in sich geschlossene neue, von älteren Richtungen inhaltlich klar abgrenzbare Lehre.
Starkes Interesse an pythagoreischen Ideen zeigte Marcus Terentius Varro, der berühmteste römische Universalgelehrte. Er wurde gemäß seiner testamentarischen Verfügung „nach pythagoreischer Sitte“ beigesetzt.[51]
In der von Quintus Sextius im 1. Jahrhundert v. Chr. in Rom gegründeten Philosophenschule der Sextier wurden neben stoischen auch neupythagoreische Lehren, darunter der Vegetarismus, vertreten. Dieser (allerdings kurzlebigen) Schule gehörte Sotion, der Lehrer Senecas, an. Von den Sextiern übernahm Seneca die pythagoreische Übung der Rekapitulation des Tages am Abend, mit der man für sich Bilanz zog. Dazu gehörte eine Selbstbefragung mit Fragen wie: „Welches deiner (charakterlichen) Übel hast du heute geheilt? Welchem Laster hast du widerstanden? In welcher Hinsicht bist du besser (geworden)?“[52]
Der Dichter Ovid gab im 15. Buch seiner Metamorphosen einem fiktiven Lehrvortrag des Pythagoras breiten Raum und trug damit zur Verbreitung von pythagoreischem Gedankengut bei, doch gibt es keinen Beleg für die Annahme, dass er selbst Neupythagoreer war.
1917 wurde in Rom in der Nähe der Porta Maggiore ein unterirdisches Bauwerk in Form einer Basilika aus der Zeit des Kaisers Claudius (41–54) entdeckt. Es sollte offenbar als Versammlungsraum für einen religiösen Zweck dienen, wurde aber schon bald nach dem Ende der Bauarbeiten geschlossen. Der Historiker und Archäologe Jérôme Carcopino hat eine Reihe von Indizien gesammelt, die dafür sprechen, dass die Erbauer Neupythagoreer waren.[53] Dazu gehört unter anderem die Ausschmückung von Decken und Wänden mit Darstellungen von Szenen aus der Mythologie, die dem Betrachter den als Erlösung aufgefassten Tod und das nachtodliche Schicksal der Seele vor Augen führen.
Der bekannteste Neupythagoreer der römischen Kaiserzeit war Apollonios von Tyana (1. Jahrhundert n. Chr.). Von seiner Philosophie ist wenig Zuverlässiges überliefert. Er orientierte sich offenbar in seiner philosophischen Lebensführung stark am Vorbild des Pythagoras (bzw. an dem damals dominierenden Pythagorasbild) und beeindruckte damit seine Zeitgenossen und die Nachwelt nachhaltig.
Die übrigen Neupythagoreer waren zugleich Platoniker bzw. Neuplatoniker. Im Neupythagoreismus waren frühpythagoreische Ideen mit Legenden aus der späteren pythagoreischen Tradition und (neu)platonischen Lehren verschmolzen. Moderatos von Gades (1. Jahrhundert n. Chr.) betrachtete die Zahlenlehre als didaktisches Mittel zur Veranschaulichung von Erkenntnisgegenständen der geistigen Welt. Von Nikomachos von Gerasa (2. Jahrhundert) stammen eine Einführung in die Arithmetik (d. h. in die pythagoreische Zahlenlehre), die Schulbuch wurde und im Mittelalter in der lateinischen Fassung des Boethius sehr verbreitet war, und ein Handbuch der musikalischen Harmonik. Boethius ging in seiner für das Mittelalter maßgeblichen lateinischen Darstellung der Musiktheorie (De institutione musica) von den musikalischen Lehren des Nikomachos aus und behandelte auch die Sphärenharmonie.[54] Außerdem verfasste Nikomachos eine Biographie des Pythagoras, die verloren ist. Im 2. Jahrhundert lebte auch der Platoniker Numenios von Apameia, der den Pythagoreismus mit der authentischen Lehre Platons gleichsetzte und auch aus Sokrates einen Pythagoreer machte; den späteren Platonikern warf er vor, von Platons pythagoreischer Philosophie abgewichen zu sein.[55]
Der Neuplatoniker Porphyrios schrieb im 3. Jahrhundert eine Lebensbeschreibung des Pythagoras und zeigte sich besonders in seinem Eintreten für den Vegetarismus pythagoreisch beeinflusst. Weit stärker trat pythagoreisches Gedankengut bei dem etwas jüngeren Neuplatoniker Iamblichos von Chalkis in den Vordergrund. Er verfasste ein zehnbändiges Werk über die pythagoreische Lehre, von dem Teile erhalten sind, darunter insbesondere die Abhandlung „Vom pythagoreischen Leben“. Sein Pythagorasbild war von einer Fülle von legendenhaftem Stoff geprägt, den er zusammentrug. Sein Anliegen war insbesondere, die metaphysisch-religiöse und die ethische Seite des Pythagoreismus mit der Mathematik (worunter er primär die arithmetische und geometrische Symbolik verstand) zu verbinden und dieses Ganze als göttliche Weisheit darzustellen, die den Menschen durch Pythagoras geschenkt sei. Wie Numenios betrachtete er Platons Lehre nur als Ausgestaltung der pythagoreischen Philosophie.[56]
Im 5. Jahrhundert schrieb der Neuplatoniker Hierokles von Alexandria einen Kommentar zu den „Goldenen Versen“. Er betrachtete dieses Gedicht als allgemeine Einführung in die Philosophie. Unter Philosophie verstand er einen Platonismus, den er mit Pythagoreismus gleichsetzte.[57] Auch der Neuplatoniker Syrianos, ein Zeitgenosse des Hierokles, war überzeugt, dass Platonismus nichts anderes als Pythagoreismus sei.[58]
Neuzeitliche Rezeption
Seit der Renaissance haben einzelne Naturphilosophen so stark pythagoreisches Gedankengut rezipiert und sich so nachdrücklich zur pythagoreischen Tradition bekannt, dass man sie als Pythagoreer bezeichnen kann. Ihnen ging und geht es darum, das Universum als einen nach mathematischen Regeln sinnvoll und ästhetisch durchstrukturierten Kosmos zu erweisen. Diese harmonische Ordnung soll in den Planetenbahnen ebenso wie in musikalischen Proportionen und in der Zahlensymbolik erkennbar sein. Die Gesetze der Harmonie werden als grundlegende Prinzipien betrachtet, die in der gesamten Natur auffindbar seien. Zu dieser Denkweise bekannten sich bedeutende Humanisten wie Giovanni Pico della Mirandola (1463–1494), der sich ausdrücklich als Pythagoreer bezeichnete,[59] und Johannes Reuchlin (1455–1522). Einen Vorläufer hatten sie in dem spätmittelalterlichen Gelehrten Pietro d’Abano.[60] Besonders eifrig bemühte sich der Astronom und Naturphilosoph Johannes Kepler (1571–1630), die Planetenbewegungen als Ausdruck einer vollkommenen Weltharmonie zu erweisen und astronomische Proportionen mit musikalischen zu verbinden.[61]
Im 20. Jahrhundert knüpfte der Musikwissenschaftler Hans Kayser mit seiner „harmonikalen Grundlagenforschung“ an die pythagoreische Tradition an. Sein Schüler Rudolf Haase setzte seine Arbeit fort. Diese Bemühungen finden insbesondere in Kreisen der Esoterik Anklang. Da die Grundannahme einer kosmischen Harmonie, von der die modernen Pythagoreer ausgehen, den Charakter einer religiösen Überzeugung hat, finden ihre Forschungen in der Wissenschaft kaum Beachtung.
Werner Heisenberg wies in seinem erstmals 1937 veröffentlichten Aufsatz „Gedanken der antiken Naturphilosophie in der modernen Physik“ den Pythagoreern eine Pionierrolle bei der Entstehung der naturwissenschaftlichen Denkweise zu, welche darauf abzielt, die Ordnung in der Natur mathematisch zu fassen. Heisenberg schrieb, die „Entdeckung der mathematischen Bedingtheit der Harmonie“ durch die Pythagoreer beruhe auf „dem Gedanken an die sinngebende Kraft mathematischer Strukturen“, einem „Grundgedanken, den die exakte Naturwissenschaft unserer Zeit aus der Antike übernommen hat“; die moderne Naturwissenschaft sei „eine konsequente Durchführung des Programms der Pythagoreer“. Die Entdeckung der rationalen Zahlenverhältnisse, die der musikalischen Harmonie zugrunde liegen, gehört für Heisenberg „zu den stärksten Impulsen menschlicher Wissenschaft überhaupt“.[62]
Die spanische Philosophin María Zambrano (1904–1991) sah im Pythagoreismus eine Ausrichtung des Denkens, welche die Wirklichkeit in Zahlenverhältnissen sucht und damit das Universum als „ein Gewebe aus Rhythmen, eine körperlose Harmonie“ betrachtet, worin die Dinge nicht in sich selbst bestehen, sondern nur durch ihre mathematischen und zeitlichen Beziehungen zueinander Phänomene in Erscheinung treten lassen. Den Gegenpol dazu bilde der Aristotelismus, für den die einzelnen Dinge als Substanzen in sich ruhen und damit eine eigene innere Wirklichkeit aufweisen. Der Aristotelismus habe zwar gesiegt, da er zunächst eine überlegene Erklärung der Natur und des Lebens anbieten konnte, aber die pythagoreische Haltung existiere als Alternative weiter und die moderne Physik der Relativität sei eine Rückkehr zu ihr.[63]
Siehe auch
Quellensammlungen
- Laura Gemelli Marciano (Hrsg.): Die Vorsokratiker. Band 1, Artemis & Winkler, Düsseldorf 2007, ISBN 978-3-7608-1735-4, S. 100–220 (griechische Quellentexte mit deutscher Übersetzung und Erläuterungen)
- Maurizio Giangiulio (Hrsg.): Pitagora. Le opere e le testimonianze. 2 Bände, Mondadori, Milano 2001–2002, ISBN 88-04-47349-5 (griechische Texte mit italienischer Übersetzung)
- Jaap Mansfeld, Oliver Primavesi (Hrsg.): Die Vorsokratiker. Reclam, Stuttgart 2011, ISBN 978-3-15-010730-0, S. 122–205 (griechische Texte mit deutscher Übersetzung; die Einleitung entspricht teilweise nicht dem aktuellen Forschungsstand)
- Maria Timpanaro Cardini (Hrsg.): Pitagorici. Testimonianze e frammenti. 3 Bände, La Nuova Italia, Firenze 1958–1964 (griechische und lateinische Texte mit italienischer Übersetzung)
Literatur
Handbuchdarstellungen
- Constantinos Macris: Pythagore de Samos (Compléments). In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques. Band 7, CNRS Éditions, Paris 2018, ISBN 978-2-271-09024-9, S. 1025–1174
- Irmgard Männlein-Robert: Der Neupythagoreismus. In: Christoph Riedweg u. a. (Hrsg.): Philosophie der Kaiserzeit und der Spätantike (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Band 5/1). Schwabe, Basel 2018, ISBN 978-3-7965-3698-4, S. 633–638, 698 f.
- Johan C. Thom: Pythagoras (Pythagoreer). In: Reallexikon für Antike und Christentum. Band 28, Hiersemann, Stuttgart 2018, ISBN 978-3-7772-1815-1, Sp. 496–522
- Leonid Zhmud: Pythagoras und die Pythagoreer. 2. Die Pythagoreer. In: Hellmut Flashar u. a. (Hrsg.): Frühgriechische Philosophie (= Grundriss der Geschichte der Philosophie. Die Philosophie der Antike. Band 1). Halbband 1, Schwabe, Basel 2013, ISBN 978-3-7965-2598-8, S. 401–429.
Gesamtdarstellungen, Untersuchungen
- Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon. Hans Carl, Nürnberg 1962
- Walter Burkert: Lore and Science in Ancient Pythagoreanism. Harvard University Press, Cambridge (Mass.) 1972, ISBN 0-674-53918-4 (überarbeitete Fassung von Burkerts Weisheit und Wissenschaft)
- Gabriele Cornelli: In Search of Pythagoreanism. Pythagoreanism As an Historiographical Category. De Gruyter, Berlin 2013, ISBN 978-3-11-030627-9
- Cornelia Johanna de Vogel: Pythagoras and Early Pythagoreanism. An Interpretation of Neglected Evidence on the Philosopher Pythagoras. Van Gorcum, Assen 1966
- Frank Jacob: Die Pythagoreer: Wissenschaftliche Schule, religiöse Sekte oder politische Geheimgesellschaft? In: Frank Jacob (Hrsg.): Geheimgesellschaften: Kulturhistorische Sozialstudien (= Globalhistorische Komparativstudien, Bd. 1), Königshausen & Neumann, Würzburg 2013, S. 17–34
- Charles H. Kahn: Pythagoras and the Pythagoreans. A Brief History. Hackett, Indianapolis 2001, ISBN 0-87220-576-2
- James A. Philip: Pythagoras and Early Pythagoreanism. University of Toronto Press, Toronto 1968, ISBN 0-8020-5175-8
- Christoph Riedweg: Pythagoras: Leben, Lehre, Nachwirkung. Eine Einführung. 2. Auflage, Beck, München 2007, ISBN 978-3-406-48714-9
- Bartel Leendert van der Waerden: Die Pythagoreer. Artemis, Zürich und München 1979, ISBN 3-7608-3650-X
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Akademie Verlag, Berlin 1997, ISBN 3-05-003090-9
- Leonid Zhmud: Pythagoras and the Early Pythagoreans. Oxford University Press, Oxford 2012, ISBN 978-0-19-928931-8
Aufsatzsammlungen
- Gabriele Cornelli u. a. (Hrsg.): On Pythagoreanism. De Gruyter, Berlin 2013, ISBN 978-3-11-031845-6
Bibliographie
- Luis E. Navia: Pythagoras. An Annotated Bibliography. Garland, New York 1990, ISBN 0-8240-4380-4
Weblinks
- Eintrag in Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Anmerkungen
- Siehe zur Datierung Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 176; Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 21–23; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 51f.
- Diodor 12,9,5–6; Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 203–206.
- Siehe zu diesen Ereignissen Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 207–217 und Kurt von Fritz: Pythagorean Politics in Southern Italy, New York 1940, S. 88–90.
- Kurt von Fritz: Pythagorean Politics in Southern Italy, New York 1940, S. 94ff., 108; Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 201f., 207; etwas abweichend Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 190f.
- Alfonso Mele: Magna Grecia, Napoli 2007, S. 259–298; Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 149f.
- Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 20–24.
- Vereinzelt nennen späte Autoren (darunter Iamblichos, De vita Pythagorica 265f.) Namen von angeblichen Nachfolgern. Quellen nennt Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 180 Anm. 35 und 36.
- Kurt von Fritz: Pythagorean Politics in Southern Italy, New York 1940, S. 29–32, 97–99.
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 217–222; Kurt von Fritz: Pythagorean Politics in Southern Italy, New York 1940, S. 69–92; Christoph Riedweg: Pythagoras, 2. Auflage, München 2007, S. 137–139. Für Spätdatierung der Verfolgung (um 440/420) plädiert Domenico Musti: Le rivolte antipitagoriche e la concezione pitagorica del tempo. In: Quaderni Urbinati di cultura classica N.S. 36, 1990, S. 35–65.
- Zur Begriffsgeschichte siehe Kurt von Fritz: Mathematiker und Akusmatiker bei den alten Pythagoreern, München 1960, S. 20f.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 190f.; Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 69–73; anders jedoch Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 100–104.
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 64–70.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 191.
- Antike Belege sind zusammengestellt von Arthur S. Pease (Hrsg.): M Tulli Ciceronis de natura deorum liber primus, Cambridge (Mass.) 1955, S. 149f.
- Seneca, Epistulae 52,10; Diogenes Laertios 8,10; Gellius, Noctes Atticae 1,9; Apuleius, Florida 15; Porphyrios, Vita Pythagorae 13 und 54; Iamblichos, De vita Pythagorica 71–72 und 74.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 431–440; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 170–175.
- Christian Mann: Athlet und Polis im archaischen und frühklassischen Griechenland, Göttingen 2001, S. 175–177.
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 70, 229, 231.
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 42f., 70f., 235f., 239f.
- Alfons Städele: Die Briefe des Pythagoras und der Pythagoreer, Meisenheim 1980, S. 288ff.
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 153, 212; Christoph Riedweg: Pythagoras, 2. Auflage, München 2007, S. 151f.
- Siehe zu dieser Idee Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 251f.; Carl A. Huffman: Philolaus of Croton, Pythagorean and Presocratic, Cambridge 1993, S. 330–332.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 110f.
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 116ff.
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 252–268.
- Johan C. Thom: The Pythagorean Golden Verses, Leiden 1995, S. 94–99 (griechischer Text und englische Übersetzung).
- Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 232–234; Clara Talamo: Pitagora e la ΤΡΥΦΗ. In: Rivista di filologia e di istruzione classica 115, 1987, S. 385–404.
- Griechisch ἀποχὴ ἐμψύχων. Iamblichos, De vita Pythagorica 107; 168; 225; Porphyrios, Vita Pythagorae 7 (mit Berufung auf Eudoxos von Knidos).
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 52f.
- Johannes Haußleiter: Der Vegetarismus in der Antike, Berlin 1935, S. 97–157; Carmelo Fucarino: Pitagora e il vegetarianismo, Palermo 1982, S. 21–31.
- Zum Forschungsstand siehe Giovanni Sole: Il tabù delle fave, Soveria Mannelli 2004. Vgl. Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 169–171; Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 164–166; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 127f.
- Iamblichos, De vita Pythagorica 229–230. Siehe auch Johan C. Thom: „Harmonious Equality“: The Topos of Friendship in Neopythagorean Writings. In: John T. Fitzgerald (Hrsg.): Greco-Roman Perspectives on Friendship, Atlanta 1997, S. 77–103.
- Zu der Legende und ihrer Rezeption siehe Ernst Gegenschatz: Die 'pythagoreische Bürgschaft' – zur Geschichte eines Motivs von Aristoxenos bis Schiller. In: Peter Neukam (Hrsg.): Begegnungen mit Neuem und Altem, München 1981, S. 90–154.
- Edwin L. Minar: Pythagorean Communism. In: Transactions and Proceedings of the American Philological Association 75, 1944, S. 34–46; Manfred Wacht: Gütergemeinschaft. In: Reallexikon für Antike und Christentum, Bd. 13, Stuttgart 1986, Sp. 1–59, hier: 2–4.
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 261–279.
- Carl A. Huffman: Philolaus of Croton, Pythagorean and Presocratic, Cambridge 1993, S. 37ff., 56ff.; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 263f. Für ein ontologisches Verständnis der Zahlenlehre plädiert jedoch Hermann S. Schibli: On ‚The One‘ in Philolaus, Fragment 7. In: The Classical Quarterly 46, 1996, S. 114–130. Vgl. auch Charles H. Kahn: Pythagoras and the Pythagoreans. A Brief History, Indianapolis 2001, S. 28.
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 337–363, 392ff.; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 153ff.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 293–295.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 300f.
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 213–224; Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 427–438.
- Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 100–103, 110f., 434f.
- Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 219–225.
- Barbara Münxelhaus: Pythagoras musicus, Bonn 1976, S. 25–29, 36–39, 50–55, 57ff.; Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 366–372.
- Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 350–352.
- Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 162–166; Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 364f.; Walter Burkert: Weisheit und Wissenschaft, Nürnberg 1962, S. 355; Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 181–183, 233.
- Carl A. Huffman: Philolaus of Croton, Pythagorean and Presocratic, Cambridge 1993 bietet eine Edition der Philolaos-Fragmente mit Kommentar; zur Philosophie S. 37ff.
- Christoph Riedweg: Pythagoras, 2. Auflage, München 2007, S. 152–157; Charles H. Kahn: Pythagoras and the Pythagoreans. A Brief History, Indianapolis 2001, S. 63–71. Zu Platons Verhältnis zu Archytas siehe auch Carl A. Huffman: Archytas of Tarentum, Cambridge 2005, S. 32–42.
- Textstellen und Kommentar bei Maurizio Giangiulio (Hrsg.): Pitagora. Le opere e le testimonianze, Band 2, Milano 2000, S. 183–199; siehe auch Bartel Leendert van der Waerden: Die Pythagoreer, Zürich 1979, S. 182–185.
- Bruno Centrone: Introduzione a i pitagorici, Roma 1996, S. 52.
- Der Traditionsbruch wird von Cicero (Timaeus 1) bezeugt; dies schließt einzelne pythagoreische Aktivitäten in Italien im 3. und 2. Jahrhundert v. Chr. nicht aus. Siehe dazu Cornelia J. de Vogel: Pythagoras and Early Pythagoreanism, Assen 1966, S. 28ff.
- Zum neupythagoreischen Gedankengut bei Varro siehe Yves Lehmann: Varron théologien et philosophe romain, Bruxelles 1997, S. 299–314; Leonardo Ferrero: Storia del pitagorismo nel mondo romano, 2. Auflage, Forlì 2008, S. 291–304; Burkhart Cardauns: Marcus Terentius Varro. Einführung in sein Werk, Heidelberg 2001, S. 70f.
- Seneca, De ira 3,36,1–3.
- Jérôme Carcopino: La basilique pythagoricienne de la Porte Majeure, Paris 1927.
- Ubaldo Pizzani: Studi sulle fonti del „De Institutione Musica“ di Boezio. In: Sacris erudiri 16, 1965, S. 5–164, hier: 27ff.
- Dominic J. O’Meara: Pythagoras Revived. Mathematics and Philosophy in Late Antiquity, Oxford 1989, S. 10–14.
- Siehe hierzu die gründliche Untersuchung von Gregor Staab: Pythagoras in der Spätantike. Studien zu De Vita Pythagorica des Iamblichos von Chalkis, München 2002 (mit Gesamtübersicht über den sonstigen kaiserzeitlichen Neupythagoreismus S. 75–143).
- Dominic J. O’Meara: Pythagoras Revived. Mathematics and Philosophy in Late Antiquity, Oxford 1989, S. 114–118.
- Dominic J. O’Meara: Pythagoras Revived. Mathematics and Philosophy in Late Antiquity, Oxford 1989, S. 119ff.
- Paolo Casini: L’antica sapienza italica. Cronistoria di un mito, Bologna 1998, S. 56–61.
- Christiane Joost-Gaugier: Measuring Heaven. Pythagoras and His Influence on Thought and Art in Antiquity and the Middle Ages, Ithaca 2006, S. 130.
- Ekkehart Schaffer: Die pythagoreische Tradition. Studien zu Platon, Kepler und Hegel, Köln 2004, S. 65–98; Charles H. Kahn: Pythagoras and the Pythagoreans. A Brief History, Indianapolis 2001, S. 162–171.
- Werner Heisenberg: Gedanken der antiken Naturphilosophie in der modernen Physik. In: Werner Heisenberg: Wandlungen in den Grundlagen der Naturwissenschaft, 8., erweiterte Auflage, Stuttgart 1949, S. 47–53, hier: 50f.
- María Zambrano: Der Mensch und das Göttliche, Wien 2005, S. 64–99.