Datenkompression
Die Datenkompression (wohl lehnübersetzt und eingedeutscht aus dem englischen ‚data compression‘) – auch (weiter eingedeutscht) Datenkomprimierung[1] genannt – ist ein Vorgang, bei dem die Menge digitaler Daten verdichtet oder reduziert wird. Dadurch sinkt der benötigte Speicherplatz, und die Übertragungszeit der Daten verkürzt sich. In der Nachrichtentechnik wird die Komprimierung von Nachrichten aus einer Quelle durch einen Sender als Quellenkodierung bezeichnet.[2][3]
Grundsätzlich wird bei der Datenkompression versucht, redundante Informationen zu entfernen. Dazu werden die Daten in eine Darstellung überführt, mit der sich alle – oder zumindest die meisten – Informationen in kürzerer Form darstellen lassen. Diesen Vorgang übernimmt ein Kodierer und man bezeichnet den Vorgang als Kompression oder Komprimierung. Die Umkehrung bezeichnet man als Dekompression oder Dekomprimierung.
Man spricht von verlustfreier Kompression, verlustfreier Kodierung oder Redundanzreduktion, wenn aus den komprimierten Daten wieder exakt die Originaldaten gewonnen werden können. Das ist beispielsweise bei der Kompression ausführbarer Programmdateien notwendig.
Bei der verlustbehafteten Kompression oder Irrelevanzreduktion können die Originaldaten aus den komprimierten Daten meist nicht mehr exakt zurückgewonnen werden, das heißt, ein Teil der Information geht verloren; die Algorithmen versuchen, möglichst nur „unwichtige“ Informationen wegzulassen. Solche Verfahren werden häufig zur Bild- oder Videokompression und Audiodatenkompression eingesetzt.
Allgemein
Datenkompression findet heutzutage bei den meisten Fernübertragungen digitaler Daten statt. Sie hilft, Ressourcen bei der Übertragung oder Speicherung von Daten einzusparen, indem sie in eine Form verwandelt werden, die – abhängig von der Anwendung – möglichst minimal ist. Dabei können verlustlos nur Daten komprimiert werden, die in irgendeiner Form redundant sind. Ist keine Redundanz vorhanden – zum Beispiel bei völlig zufälligen Daten – ist verlustlose Kompression wegen der Kolmogorov-Komplexität prinzipiell unmöglich. Ebenso verbietet das Taubenschlagprinzip, dass jede beliebige Datei verlustlos komprimiert werden kann. Hingegen ist verlustbehaftete Kompression immer möglich: Ein Algorithmus ordnet die Daten danach, wie wichtig sie sind und verwirft die „unwichtigen“ dann. In der Auflistung, wie wichtig welche Bestandteile sind, kann stets mehr verworfen werden, indem die „Behalten-Schwelle“ entsprechend verschoben wird.
Bei der Datenkompression ist sowohl auf Sender- als auch auf Empfängerseite Berechnungsaufwand nötig, um die Daten zu komprimieren oder wiederherzustellen. Der Berechnungsaufwand ist jedoch bei verschiedenen Kompressionsmethoden sehr unterschiedlich. So sind etwa Deflate und LZO sowohl bei Kompression und Dekompression sehr schnell, während etwa LZMA unter großem Aufwand eine besonders weitgehende Kompression – und somit möglichst kleine Datenmengen – erzielt, während komprimierte Daten sehr schnell wieder in die ursprüngliche Form zurückgewandelt werden können. Dies erzwingt je nach Anwendungsgebiet eine unterschiedliche Wahl der Kompressionsmethode. Daher sind Kompressionsmethoden entweder auf Datendurchsatz, Energiebedarf oder die Datenreduktion optimiert, und die Kompression hat somit nicht immer eine möglichst kompakte Darstellung als Ziel. Deutlich wird der Unterschied bei diesen Beispielen:
- Werden Video- oder Tonaufnahmen live gesendet, müssen Kompression und Wiederherstellung möglichst schnell durchgeführt werden. Qualitätseinbußen sind vertretbar, wenn dafür die maximale (mögliche) Übertragungsrate eingehalten wird. Dies gilt beispielsweise für Telefongespräche, wo der Gesprächspartner oft auch bei schlechter Tonqualität noch verstanden wird.
- Wird eine einzelne Datei von unzähligen Nutzern heruntergeladen, lohnt sich ein langsamer, aber sehr leistungsfähiger Kompressions-Algorithmus. Die reduzierte Bandbreite bei der Übertragung macht den Zeitaufwand der Kompression leicht wett.
- Bei der Datensicherung und der Archivierung von Daten muss ein Algorithmus verwendet werden, der gegebenenfalls auch in ferner Zukunft verwendet wird. In diesem Fall kommen nur verbreitete, bewährte Algorithmen in Frage, die mitunter nicht die besten Kompressionsraten aufweisen.
- Auch die Art der Daten ist relevant für die Auswahl der Kompressionsmethode. Zum Beispiel haben die beiden auf unixoiden Betriebssystemen gebräuchlichen Kompressions-Programme gzip und bzip2 die Eigenschaften, dass gzip nur 32.000 Bytes große Blöcke komprimiert, während bzip2 900.000 Bytes Blockgröße aufweist. Redundante Daten werden nur innerhalb dieser Blöcke komprimiert.
Mitunter werden die Daten vor der Kompression noch in eine andere Darstellung transformiert. Das ermöglicht einigen Verfahren die Daten anschließend effizienter zu komprimieren. Dieser Vorverarbeitungsschritt wird Präkodierung genannt. Ein Beispiel dafür ist die Burrows-Wheeler-Transformation und Move to front bei bzip2.[4]
Das Fachgebiet der Datenkompression überschneidet sich zum Teil mit Informationstheorie und künstlicher Intelligenz, und im Bereich der verlustbehafteten Datenkompression auch mit Wahrnehmungspsychologie (s. weiter unten). Informationstheorie ist insofern betroffen, weil die Dateigröße eines bestmöglich komprimierten Datensatzes direkt den Informationsgehalt dieses Datensatzes angibt.
Kann ein Kompressionsalgorithmus lernen, unter welchen Umständen auf die Zeichenkette "ABC" ein "D" folgt, muss das "D" in der komprimierten Datei gar nicht gespeichert werden – bei der Wiederherstellung der ursprünglichen Datei weiß der Algorithmus, an welchen Stellen ein "D" einzufügen ist. Obwohl noch kein derartiger Kompressionsalgorithmus in der Praxis verwendet wird, sind diverse Kompressionsverfahren, die künstliche neuronale Netzwerke und maschinelles Lernen verwenden, in Entwicklung.[5]
Verlustbehaftete Kompression
Verlustbehaftete Kompression ist, wie oben beschrieben, stets möglich – die Schwelle, was als „redundant“ gilt, kann so lange heraufgesetzt werden, bis nur noch 1 Bit übrig bleibt. Die Grenzen sind fließend und werden durch den Anwendungsfall bestimmt: Zum Beispiel könnte "Das Haus ist groß" zu "Das Haus ist gr" komprimiert werden; will der Leser wissen "welche Eigenschaft hat das Haus?", so ist nicht mehr unterscheidbar, ob es "grau", "grün" oder "groß" ist. Will der Leser wissen "wurde etwas über ein Haus gesagt?", so kann das noch immer eindeutig bejaht werden.
Bei verlustbehafteter Bildkompression gehen zunehmend Details verloren/werden unscharf, schließlich „verschwimmt alles“ zu einer Fläche mit einheitlicher Farbe; eine Audio-Aufnahme wird meist dumpfer und undeutlicher, sie würde nach größtmöglicher Kompression bei den meisten Algorithmen nur noch einen einfachen Sinuston aufweisen.
Verlustfreie Kompression
Bei verlustfreier Kompression gelten sehr viel engere Grenzen, da gewährleistet sein muss, dass die komprimierte Datei wieder in die Originaldatei rücktransformiert werden kann.
Die Kolmogorow-Komplexität befasst sich mit der kleinstmöglichen "Anleitung", die notwendig ist, um aus den komprimierten Daten die Originaldaten wiederherzustellen. So zum Beispiel lässt sich die Zahl "100000000000000000000000000000000000" sehr einfach komprimieren: "Schreibe 1 und dann 35 Nullen", was eine Kompression von 36 auf 29 Zeichen darstellt. Ebenfalls lassen sich beliebig viele Nachkommastellen der Kreiszahl Pi mit ihrer Berechnungsvorschrift komprimieren – wobei der Kompressionsalgorithmus dann erkennen müsste, dass es sich um die Zahl Pi handelt. Zu beachten ist, dass bei komprimierten Dateien der Wiederherstellungs-Algorithmus ebenfalls zur Dateigröße hinzugerechnet werden müsste, da jede komprimierte Datei ohne einen solchen Algorithmus wertlos ist. So ließe sich die obige Zahl auch mit "10^35" oder "1e35" komprimieren, wobei dann der Leser von der Wiederherstellungsmethode, nämlich der Potenzschreibweise, Kenntnis haben muss. Weist eine Zeichenkette aber keinerlei erkennbare Struktur/Besonderheiten auf, dann ist eine Kompression nicht möglich – die Anleitung müsste die unveränderten Originaldaten beinhalten.
Ein weiterer Grund für die Unkomprimierbarkeit mancher Daten ist das sogenannte Taubenschlagprinzip: Gibt es weniger Nistplätze für Tauben als es Tauben im Taubenschlag gibt, müssen sich zwangsläufig zwei oder mehr Tauben einen Nistplatz teilen. Auf einem n bit großen Speicherplatz kann man eine von 2n möglichen Informationen abspeichern, und auf einem Speicherplatz, der um ein bit kleiner ist, kann man folglich nur eine von halb so viel möglichen Informationen speichern: 16 bits → 216 = 65536 mögliche Informationen, 15 bits → 215 = 32768 mögliche Informationen. Unter der Annahme, man könne jede mögliche Datei um ein bit verkleinern, würde dies nach dem Taubenschlagprinzip bedeuten, dass jeder Speicherplatz gleichzeitig zwei verschiedene komprimierte Dateien enthalten müsste. Da aber in der verlustfreien Kompression eine umkehrbar eindeutige Zuordnung zwischen komprimierter und unkomprimierter Datei bestehen muss, verbietet sich dies.
Gälte das Taubenschlagprinzip nicht, und gäbe es einen Algorithmus, der jede beliebige Datei um mindestens ein Bit komprimieren kann, könnte dieser rekursiv auf die jeweils komprimierte Datei angewendet werden – jede beliebige Information ließe sich auf 0 bit reduzieren. In der Praxis lassen sich nur dann bereits komprimierte Daten nochmals komprimieren, wenn im vorherigen Durchlauf ein nicht 100%ig effizienter Algorithmus verwendet wurde, welcher die Redundanz noch nicht vollständig entfernt hat (z. B. eine sehr große Datei voller Nullen wird zwei Mal mit gzip komprimiert).
Aus diesen beiden Tatsachen ergibt sich die Schlussfolgerung, dass rein zufällige Daten (höchstwahrscheinlich) unkomprimierbar sind (da sie zumeist keine Struktur aufweisen), und dass zwar viele, aber nicht alle, Daten komprimiert werden können. Zwei Preisgelder, 100 Dollar für die erfolgreiche Kompression von einer Million zufälliger Ziffern[6][7] und 5000 Dollar für die erfolgreiche Kompression einer Datei beliebiger Länge, die vom Preisstifter, Mike Goldman, erzeugt wird,[8] wurden bis heute nicht ausbezahlt.
Verlustfreie Kompression
Bei der verlustfreien Kompression können die Originaldaten exakt aus den komprimierten Daten wiederhergestellt werden. Dabei geht keinerlei Information verloren. Im Wesentlichen nutzen verlustfreie Kompressionsverfahren die Redundanz von Daten aus, man spricht auch von Redundanzreduktion.
Die theoretische Grundlage bildet die Informationstheorie (verwandt mit der algorithmischen Informationstheorie). Sie gibt durch den Informationsgehalt eine minimale Anzahl an Bits vor, die zur Kodierung eines Symbols benötigt werden. Verlustlose Kompressionsverfahren versuchen nun Nachrichten so zu kodieren, dass sie sich ihrer Entropie möglichst gut annähern.
Text
Texte, sofern sie aus Buchstaben bestehen oder als Zeichenketten abgespeichert sind, und somit nicht als Bild (Rastergrafik, typischerweise eine Bilddatei nach dem Einscannen eines Buches), belegen vergleichsweise wenig Speicherplatz. Dieser lässt sich durch ein Verfahren zur verlustfreien Kompression auf 20 % bis 10 % des ursprünglich von ihr benötigten Platzes reduzieren.
Beispiele:
Ausgangstext: AUCH EIN KLEINER BEITRAG IST EIN BEITRAG Kodiertext: AUCH EIN KLEINER BEITRAG IST /2 /4
Hier wurde erkannt, dass die Wörter EIN und BEITRAG zweimal auftauchen, und dadurch angegeben, dass diese mit den gerade zurückliegenden übereinstimmen. Bei genauerer Betrachtung könnte dann auch das in KLEINER enthaltene EIN entsprechend kodiert werden.
Wörterbuchmethode
Verwandt ist die tokenbasierte Kompression. Häufig wiederkehrende Schlüsselwörter werden durch Abkürzungen, Tokens, ersetzt.
Ausgangstext: Print "Hallo"; Print "Hier" Kodiertext: 3F "Hallo"; 3F "Hier"
Für die Zuordnung der Tokens zu den eigentlichen Wörtern muss entweder ein externes Wörterbuch vorhanden sein, oder in der komprimierten Datei ersichtlich/mit enthalten sein.
Run length encoding (RLE)
Bei der RLE, deutsch Lauflängenkodierung, werden identische Textbestandteile, die hintereinander stehen, nur einmal abgespeichert – mit der Anzahl ihrer Wiederholungen. Hier wird „ 10 Grad,“ drei Mal wiederholt:
Ausgangstext: In den letzten Tagen betrug die Temperatur 10 Grad, 10 Grad, 10 Grad, und dann 14 Grad. Kodiertext: In den letzten Tagen betrug die Temperatur/3/ 10 Grad,/ und dann 14 Grad.
Die Burrows-Wheeler-Transformation ist eine umkehrbare Operation, welche einen gegebenen Text so umformt, dass dieselben Buchstaben möglichst oft gleich hintereinander stehen. So können die Daten dann mit RLE komprimiert werden.
Entropiekodierung
Verfahren der so genannten Entropiekodierung:
- Huffman-Code (in modifizierter Form zum Beispiel für die Fax-Übertragung).
- Arithmetische Kodierung[4]
Der bekannte Morse-Code funktioniert nach einem ähnlichen Prinzip und dient als gutes Beispiel: Häufige Buchstaben der englischen Sprache (z. B. E = .) werden als kurze Codes abgespeichert, seltene als lange Codes (z. B. Q = _ _ . _).
Als Beispiel ein Ausgangstext von 66 Zeichen Länge (Datenmenge 462 Bit bei 7 Bit pro Zeichen, siehe ASCII):
WENN HINTER FLIEGEN FLIEGEN FLIEGEN, FLIEGEN FLIEGEN FLIEGEN NACH.
Eine sehr einfache, aber nicht sehr effiziente Entropiekodierung besteht darin, alle Teile einer Nachricht (siehe Tabelle; „_“ steht für das Leerzeichen) nach ihrer Häufigkeit zu sortieren, und mittels binären Zahlen zu nummerieren:
| Textteil… | …wird ersetzt durch… |
|---|---|
| _FLIEGEN | 1 |
| WENN_ | 10 |
| _NACH. | 11 |
| HINTER | 100 |
| , | 101 |
Der mit diesem Wörterbuch komprimierte Text lautet
10 100 1 1 1 101 1 1 1 11
und benötigt in binärer Kodierung 50 Bit, denn das Ergebnis enthält drei verschiedene Zeichen (0, 1 und das Trennzeichen „ “), also 2 Bit pro Zeichen. Die Trennzeichen sind hier notwendig, da dieser Code nicht präfixfrei ist. Der präfixfreie Huffman-Code, also folgendes Wörterbuch,
| Textteil… | …wird ersetzt durch… |
|---|---|
| _FLIEGEN | 1 |
| WENN_ | 011 |
| _NACH. | 010 |
| HINTER | 001 |
| , | 000 |
ist effizienter, denn es führt direkt zu einem binären Ergebnis von 18 Bit Länge:
011001111000111010
In beiden Fällen muss aber auch das Wörterbuch in der komprimierten Datei abgespeichert werden – sonst lässt sich der Ausgangstext nicht rekonstruieren.
Programmdateien
Bei Programmdateien ist es kritisch, dass sie nach erfolgter Dekomprimierung wieder im ursprünglichen Zustand sind. Andernfalls wäre eine fehlerfreie bzw. korrekte Ausführung unwahrscheinlich. Komprimierte Programmdateien sind meist selbst wieder ausführbare Dateien. Sie bestehen aus einer Routine, die den Programmcode wieder dekomprimiert und anschließend ausführt. Dadurch ist die Kompression des Programms für den Benutzer vollkommen ‚transparent‘ (er bemerkt sie nicht).
Verlustbehaftete Kompression
Bei der verlustbehafteten Kompression werden irrelevante Informationen entfernt, man spricht auch von Irrelevanzreduktion. Dabei geht ein Teil der Information aus den Originaldaten verloren, sodass aus den komprimierten Daten nicht mehr das Original rekonstruiert werden kann.
Es wird ein Modell benötigt, das entscheidet, welcher Anteil der Information für den Empfänger entbehrlich ist. Verlustbehaftete Kompression findet meist in der Bild-, Video- und Audio-Übertragung Anwendung. Als Modell wird dort die menschliche Wahrnehmung zugrunde gelegt. Ein populäres Beispiel ist das Audio-Format MP3, das Frequenzmuster entfernt, die der Mensch schlecht oder gar nicht hört.
Die theoretische Grundlage bildet die Rate-Distortion-Theorie. Sie beschreibt, welche Datenübertragungsrate mindestens nötig ist, um Informationen mit einer bestimmten Güte zu übertragen.
Bilder, Videos und Tonaufnahmen

Ton, Bild und Film sind Einsatzgebiete verlustbehafteter Kompression. Anders wären die oftmals enormen Datenmengen sehr schwer zu handhaben. Bereits die Aufnahmegeräte begrenzen das Datenvolumen. Die Reduktion der gespeicherten Daten orientiert sich an den physiologischen Wahrnehmungseigenschaften des Menschen. Die Kompression durch Algorithmen bedient sich dabei typischerweise der Wandlung von Signalverläufen von Abtastsignalen in eine Frequenzdarstellung.
In der akustischen Wahrnehmung des Menschen werden Frequenzen oberhalb von ca. 20 kHz nicht mehr wahrgenommen und können bereits im Aufnahmesystem beschnitten werden. Ebenso werden existierende, leise Nebentöne in einem Klanggemisch nur schwer wahrgenommen, wenn zur exakt gleichen Zeit sehr laute Töne auftreten, so dass die unhörbaren Frequenzanteile vom Daten-Kompressions-System entfernt werden können (siehe Psychoakustik), ohne dass dies als störend vom Hörer wahrgenommen würde. Der Mensch kann bei einer Reduktion digitalisierter, akustischer Ereignisse (Musik, Sprache, Geräusche) auf Werte um etwa 192 kbit/s (wie bei vielen Internet-Downloads) kaum oder gar keine Qualitätsunterschiede zum unkomprimierten Ausgangsmaterial (so bei einer CD) feststellen.
In der optischen Wahrnehmung des Menschen werden Farben weniger stark aufgelöst als Helligkeitsänderungen, daraus leitet sich die schon beim analogen Farbfernsehen bekannte YUV-422 Reduzierung ab. Kanten sind dagegen bedeutsamer, und es existiert eine biologische Kontrastanhebung (Machsche Streifen). Mit moderater Tiefpassfilterung zur Farbreduktion, zum Beispiel durch den auf DCT-Transformation basierenden JPEG-Algorithmus oder den neueren auf Wavelet-Transformation basierenden JPEG2000-Algorithmus, lässt sich die Datenmenge meist auf 10 % oder weniger der ursprünglichen Datenmenge reduzieren, ohne deutliche Qualitätsverringerungen.
Bewegtbilder (Filme) bestehen aus aufeinanderfolgenden Einzelbildern. Erster Ansatz war, jedes Bild einzeln gemäß JPeg-Algorithmus zu komprimieren. Das resultierende Format ist Motion JPEG (entspricht MPEG-1, wenn dieses nur I-Frames enthält). Die heutzutage sehr viel höheren Kompressionsraten sind nur erreichbar, wenn man bei der Kodierung die Ähnlichkeit von benachbarten Bildern (engl. Frames) berücksichtigt. Dazu wird das Bild in kleinere Kästchen (typische Größen liegen zwischen 4×4 und 16×16 Pixel) zerlegt und es werden ähnliche Kästchen in schon übertragenen Bildern gesucht und als Vorlage verwendet. Die Einsparung ergibt sich daraus, dass statt des gesamten Bildinhalts nur noch die Unterschiede der an sich ähnlichen Kästchen übertragen werden müssen. Zusätzlich wird aus den Änderungen vom vorherigen zum aktuellen Bild gefolgert, in welche Richtung sich Bildinhalte wie weit verschoben haben; für den entsprechenden Bereich wird dann nur ein Verschiebungsvektor gespeichert.
Kompressionsartefakte
Als Kompressionsartefakte bezeichnet man Signalstörungen, die durch die verlustbehaftete Kompression verursacht werden.
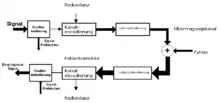
Anwendung in der Nachrichtentechnik
Bei der Datenübertragung wird häufig die zu übertragende Datenmenge durch Kompression reduziert. In so einem Fall spricht man dann auch von Quellenkodierung.[2][3] Die Quellenkodierung wird dabei häufig zusammen mit Kanalkodierung und Leitungskodierung verwendet, sollte aber nicht mit diesen verwechselt werden: Während die Quellencodierung überflüssige (redundante) Information einer Datenquelle reduziert, hat die Kanalcodierung die Aufgabe, durch zusätzlich eingebrachte Redundanz Übertragungs- bzw. Speicherfehler im Rahmen der Datenübertragung erkennen und korrigieren zu können. Die Leitungskodierung hingegen nimmt eine spektrale Anpassung des Signals an die Anforderungen des Übertragungskanals vor.
Zeittafel der Kompressions-Algorithmen
Die jahrhundertealte Stenografie kann als Datenkompression angesehen werden, welche der Handschrift eine möglichst hohe Datenrate verleiht
1833–1865 Entwicklung des Morse-Codes, welcher häufige Buchstaben in kurze Zeichen übersetzt und seltene Buchstaben in längere, was die Idee der Entropiekodierung vorzeichnet
1883 David Forsyth, Schachspieler und Journalist, publiziert eine Methode, mit welcher auf platzsparende Weise die Position von Schach-Figuren mit Lauflängenkodierung festgehalten wird → Forsyth-Edwards-Notation
1949 Informationstheorie, Claude Shannon
1952 Huffman-Kodierung, static
1964 Konzept der Kolmogorow-Komplexität
1975 Integer coding scheme, Elias
1977 Lempel-Ziv-Verfahren LZ77
1978 Lempel-Ziv-Verfahren LZ78
1979 Bereichskodierung (eine Implementierung arithmetischer Kodierung)
1982 Lempel-Ziv-Storer-Szymanski (LZSS)
1984 Lempel-Ziv-Welch-Algorithmus (LZW)
1985 Apostolico, Fraenkel, Fibonacci coding
1986 Move to front, (Bentley et al., Ryabko)
1991 Reduced Offset Lempel Ziv (ROLZ, auch LZRW4, Lempel Ziv Ross Williams)
1994 Burrows-Wheeler-Transformation (bzip2)
1995 zlib, freie Standardbibliothek für Deflate
1996 Lempel-Ziv-Oberhumer-Algorithmus (LZO), sehr schnelle Kompression
1997 Sequitur
1998 Lempel-Ziv-Markow-Algorithmus (LZMA)
2006 Hutter-Preis für beste Datenkompression
2009 PAQ, höchste Kompressionsraten auf Kosten sehr langer Laufzeit; Verwendung eines neuronalen Netzwerks (heute ZPAQ)
2011 Snappy, schneller Kodierer von Google
2011 LZ4, sehr schneller Kodierer
2013 zopfli, verbesserter Deflate-Kodierer
2015 Brotli, starke Kompression
Bekannte Methoden zur Quellcodierung
| verlustbehaftet | beides möglich | verlustfrei |
|---|---|---|
| AAC (MPEG) | ||
| Aiff | ||
| ALS (MPEG) | ||
| Apple Lossless | ||
| ATRAC | ||
| DjVu | ||
| Dolby Digital | ||
| DTS | ||
| FLAC | ||
| Monkey’s Audio | ||
| G.729 | ||
| GIF | ||
| HuffYUV | ||
| JPEG | ||
| JPEG 2000 | ||
| LA | ||
| MJPEG | ||
| MP2 (MPEG) | ||
| MP3 (MPEG) | ||
| MPEG-1 | ||
| MPEG-2 | ||
| MPEG-4 (siehe H.264, Xvid, DivX) | ||
| Musepack | ||
| PGF | ||
| PNG | ||
| TGA | ||
| TIFF | ||
| Vorbis (Ogg) | ||
| WavPack | ||
| WebP | ||
| WMA | ||
| WMV |
| Bilder | Audio | Video |
|---|
Biologie
Sinneswahrnehmungen werden gefiltert, was auch eine Art der Kompression darstellt, genauer eine verlustbehaftete Kompression, da nur aktuell relevante Informationen wahrgenommen werden. Fehlendes wird bei Bedarf unbewusst ersetzt. So sehen menschliche Augen beispielsweise nur in einem kleinen Bereich (Fovea centralis) scharf, außerhalb dieses engen Blickfeldes werden fehlende Informationen durch Muster unbewusst ersetzt. Ebenso kann das menschliche Auge Helligkeitsunterschiede wesentlich besser wahrnehmen als Unterschiede im Farbton – diesen Umstand nutzt das in JPEG-Bildern verwendete YCbCr-Farbmodell und speichert den Farbwert mit einer wesentlich geringeren Präzision ab.
Auch beim Hören werden schwache oder fehlende Signale unbewussterweise ersetzt, was sich Algorithmen wie MPEG (MP3) oder Vorbis zunutze machen.
Siehe auch
Weblinks
- Vergleich der Kompressionsleistung von über 250 Packprogrammen (englisch)
- LA – Verlustfreies Audioformat mit den angeblich höchsten Kompressionsraten (englisch)
- Data Compression – Systematisation by T. Strutz (englisch)
- Data compression FAQ (englisch)
- Lelewer, Debra, A.; Hirschberg, Daniel, S.: „Data Compression“; ACM Computing Surveys, 19, 1987, S. 261–297. Übersichtsartikel (englisch)
- Liste mit Kompressionsvergleichen (englisch)
Einzelnachweise
- Datenkomprimierung – Duden, Bibliographisches Institut; 2016
- Stefan Brunthaler: Quellen- und Leitungscodierung. (PDF; 528 kB) In: TH Wildau. 2018, abgerufen am 12. August 2018 (Vorlesungsscript Kommunikationstechnik in der Telematik SS2018).
- Peter Maluck, Jürg Scheidegger: Quellencodierung – Gelenktes Entdeckendes Lernen. (PDF; 776 kB) In: SwissEduc. 24. August 2009, abgerufen am 12. August 2018 (Seminar Kommunikationstechnik).
- Tilo Strutz: Bilddatenkompression – Grundlagen, Codierung, Wavelets, JPEG, MPEG, H.264, HEVC. Springer Vieweg, Wiesbaden 2017, ISBN 978-3-8348-1427-2, S. 421.
- Matthew V. Mahoney: Fast Text Compression with Neural Networks. In: AAAI (Hrsg.): Proceedings of the Thirteenth International Florida Artificial Intelligence Research Society Conference. 2000, ISBN 1-57735-113-4, S. 5.
- Mark Nelson: The Million Random Digit Challenge Revisited. 20. Juni 2006, abgerufen am 12. August 2018 (englisch).
- Mark Nelson: The Enduring Challenge of Compressing Random Data. DrDobbs.com, 6. November 2012, abgerufen am 12. August 2018 (englisch).
- Patrick Craig: The $5000 Compression Challenge. Abgerufen am 12. August 2018 (englisch).