Trikline Anisotropie

Die trikline Anisotropie (von altgriechisch τρία tria „drei“ und κλίνειν klinein „neigen“, „beugen“) ist die vollständige Anisotropie eines Werkstoffs/Materials, der / das im triklinen Kristallsystem – mit einer Elementarzelle wie im Bild – vorliegt.

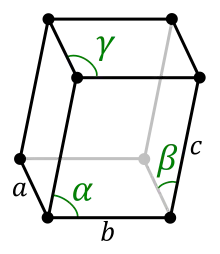
Bravais-Gitter eines triklin anisotropen Kristalls (a≠b≠c, α,β,γ≠90°)

Triklin anisotrope Materialien wie im Bild haben folgende Eigenschaften:

Das Kraft-Verformungs-Verhalten ändert sich, sobald das Material irgendwie gedreht wird.
Bei reinem Zug kommt es zu Schubverzerrungen.
Bei Scherungen treten Normal dehnungen auf.
Scherungen in einer Ebene führen zu Scherungen in anderen Ebenen.

Die Beschreibung von triklin anisotropem linear-elastischem Materialverhalten benötigt die größtmögliche Anzahl an Materialparametern, nämlich 21. Für #Thermo- und Elektromechanische Gleichgewichtseigenschaften werden höchstens 34 weitere Parameter benötigt.

Ein Material ist isotrop, wenn es richtungsunabhängig dasselbe Kraft-Verformungs-Verhalten hat. Bei anisotropen Materialien dagegen hängt das Kraft-Verformungs-Verhalten von der Belastungsrichtung ab. Die trikline Anisotropie ist die umfassendste Art der Anisotropie und enthält alle anderen Arten als Spezialfall, z. B. monokline Anisotropie (α=γ=90°) oder Orthotropie (α=β=γ=90°).

Bedeutung

Feldspate gelten als die wichtigsten gesteinsbildenden Minerale der Erdkruste und kristallisieren monoklin oder triklin.

Die kristallinen Bereiche von PET sind triklin anisotrop, ein Kunststoff, der bei Flaschen (PET-Flaschen), Folien und Textilfasern eingesetzt wird (2008 lag die Produktion bei 40 Millionen Tonnen.)

Materialtheoretische Beschreibung

Symmetriegruppe

Die Richtungsabhängigkeit eines Materials zeichnet sich dadurch aus, dass das Kraft-Verformungs-Verhalten unabhängig (invariant) ist gegenüber nur bestimmten Drehungen des Materials. Diese Drehungen bilden zusammen mit der Punktspiegelung die Symmetriegruppe des Materials.[1]^:381

Bei trikliner Anisotropie sind keinerlei Drehungen möglich, ohne dass sich das Materialverhalten ändern würde.[1]^:380

Das veranschaulichen zwei Experimente an einem Teilchen: Im ersten Experiment bringt man am Teilchen eine bestimmte Kraft auf und misst die resultierende Verformung. Im zweiten Experiment dreht man das Material irgendwie, aber nicht um Vielfache von 360°. Dann bringt man dieselbe Kraft auf wie im ersten Experiment und misst erneut die Verformung. Bei wirklich triklin anisotropem Material wird man im zweiten Experiment immer eine andere Verformung messen wie im ersten.

Die angesprochenen Drehungen werden in der Kontinuumsmechanik durch orthogonale Tensoren Q repräsentiert. Eine Symmetriegruppe g_R besteht aus denjenigen Transformationen, die die Formänderungsenergie w invariant lassen. Mathematisch wird das mit dem Verzerrungstensor E durch

\mathbf {Q} \in g_{R}\quad \leftrightarrow \quad w(\mathbf {Q\cdot E\cdot Q} ^{\top })=w(\mathbf {E} )

für alle E

ausgedrückt.[1]^:379 Darin bedeutet „·“ das Matrizenprodukt und das hochgestellte „⊤“ eine Transponierung. Mit Q gehört in der Mechanik auch -Q zur Symmetriegruppe, was durch Hinzufügen des negativen Einheitstensors -1, der eine Punktspiegelung repräsentiert, zu g_R berücksichtigt wird. Die Symmetriegruppe wird durch die Erzeugenden bestimmt, mit denen sämtliche Elemente der Gruppe durch Matrizenmultiplikation berechnet werden können. Die Symmetriegruppe des triklinen Materials ist in der Mechanik[1]^:381

g_{R}=\left\{-\mathbf {1} ,\mathbf {1} \right\}

mit Gruppenordnung 2

Diese kleinste aller möglichen mechanischen Symmetriegruppen drückt aus, dass das Material keinerlei Symmetrieeigenschaften besitzt. Der Einheitstensor ist mit -1 zwar bereits in g_R enthalten (1=(-1)·(-1)). Seine Angabe soll hier unterstreichen, dass als einzige eigentliche Drehung, die keine Drehspiegelung ist, nur die 0-Grad-„Drehung“ in der Symmetriegruppe enthalten ist.[1]^:380

Invarianten

In der isotropen Hyperelastizität hängt die Formänderungsenergie von den Hauptinvarianten I_1,2,3 des Verzerrungstensors E ab:

w(E)=w(I₁, I₂, I₃)

Die analoge Darstellung der Anisotropie erfordert, dass ein komplettes System von skalarwertigen Funktionen bekannt ist, die unter allen Transformationen in der Symmetriegruppe g_R invariant sind.[1]^:380 In der triklinen Anisotropie sind alle Komponenten des Verzerrungstensors in einem körperfesten System Invarianten:[1]^:381

E₁₁, E₂₂, E₃₃, E₁₂, E₁₃, E₂₃.

Darin ist E_ij := ê_i·E·ê_j für i,j=1,2,3 und ê_1,2,3 sind Basisvektoren einer körperfesten Orthonormalbasis. Auf diese, bei trikliner Anisotropie weitgehend beliebige Basis wird im Folgenden Bezug genommen.

Strukturvariable

Die Invarianten können mit Strukturvariablen M dargestellt werden, bei denen

\mathbf {Q} \in g_{R}\quad \leftrightarrow \quad w(\mathbf {Q\cdot E\cdot Q} ^{\top },\mathbf {Q\cdot M\cdot Q} ^{\top })=w(\mathbf {E} )

für alle E

gilt. Ihr Name rührt daher, dass die Variablen auf diese Weise die interne Struktur des Materials repräsentieren. Dieser Ansatz hat den Vorteil koordinatenunabhängig zu sein.[1]^:386f Die Strukturvariablen sind in g_R invariant[2]^:38, siehe Euklidische Transformation:

\mathbf {Q} \in g_{R}\quad \rightarrow \quad \mathbf {M} =\mathbf {Q\cdot M\cdot Q} ^{\top }

In der triklinen Anisotropie werden die beiden, zu ê_1,2 gehörenden, schiefsymmetrischen Tensoren

N=[ê₁]_×, V=[ê₂]_×

als Strukturvariablen benutzt, die im ê_1,2,3-System mit dem Kronecker-Delta δ die Darstellung

\left[{\hat {e}}_{i}\right]_{\times }:={\begin{pmatrix}0&-\delta _{i3}&\delta _{i2}\\\delta _{i3}&0&-\delta _{i1}\\-\delta _{i2}&\delta _{i1}&0\end{pmatrix}}\;\leftrightarrow \;\left[{\hat {e}}_{i}\right]_{\times }\cdot {\vec {v}}={\hat {e}}_{i}\times {\vec {v}}\quad \forall \,{\vec {v}}

besitzen, siehe Kreuzprodukt#Kreuzproduktmatrix. Aus dem Matrizenprodukt des Verzerrungstensors E mit den Strukturvariablen entstehen im ê_1,2,3-System die bereits genannten #Invarianten[2]^:54

E₁₁=Sp(E)+Sp(E·N²),	E₂₂=Sp(E)+Sp(E·V²),	E₃₃=-Sp(E)-Sp(E·N²)-Sp(E·V²),
E₂₃=Sp(E·N·V²),	E₁₃=Sp(E·N²·V),	E₁₂=Sp(E·N·V)

Triklin anisotrope lineare Elastizität

Dieser Abschnitt befasst sich mit den linearen mechanischen Eigenschaften triklin anisotroper Stoffe. Merkmale wie Wärmeausdehnung, Piezoelektrizität oder Doppelbrechung sind Gegenstand des Abschnitts #Weitere Eigenschaften.

Materialgesetz

Gegeben sind zwei Tensoren zweiter Stufe ${\boldsymbol {\sigma }}$ und ${\boldsymbol {\varepsilon }}$ mit 3×3-Koeffizienten $\sigma _{ij}$ bzw. $\varepsilon _{ij}$ . Der allgemeinste lineare Zusammenhang, den es zwischen diesen Koeffizienten gibt, ist:

f_{C}:\varepsilon _{kl}\rightarrow \sigma _{ij}=\sum _{k,l=1}^{3}C_{ijkl}\varepsilon _{kl}

.

Darin sind $C_{ijkl}$ 81 Koeffizienten mit denen die neun Komponenten $\varepsilon _{ij}$ auf neun Komponenten $\sigma _{ij}$ abgebildet werden. In der linearen Elastizitätstheorie, in der der symmetrische Spannungstensor ${\boldsymbol {\sigma }}$ eine lineare Funktion des ebenfalls symmetrischen Verzerrungstensors ${\boldsymbol {\varepsilon }}$ ist, reduziert sich die Anzahl der unabhängigen Tensor-Komponenten auf sechs, so dass nur 36 Koeffizienten unabhängig sind (wegen $C_{ijkl}=C_{ijlk}=C_{jikl}$ ). Die Hyperelastizität bewirkt die zusätzliche Symmetrie $C_{ijkl}=C_{klij}$ , sodass maximal 21 Koeffizienten ausreichen, um das Material zu beschreiben, und die werden bei der triklinen Anisotropie auch gebraucht.

Der Zusammenhang zwischen Spannungen und Verzerrungen kann in Voigt’scher Notation auch als Matrizengleichung geschrieben werden. In einem triklin anisotropen linear elastischen Material nimmt die Spannungs-Dehnungs-Beziehung bezüglich der #körperfesten Basisvektoren die Form[1]^:389

{\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\\\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}&C_{14}&C_{15}&C_{16}\\&C_{22}&C_{23}&C_{24}&C_{25}&C_{26}\\&&C_{33}&C_{34}&C_{35}&C_{36}\\&&&C_{44}&C_{45}&C_{46}\\&{\text{sym}}&&&C_{55}&C_{56}\\&&&&&C_{66}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\varepsilon _{4}\\\varepsilon _{5}\\\varepsilon _{6}\\\end{bmatrix}}

.

an. Mittels der Zuordnung 11→1, 22→2, 33→3, 23→4, 13→5 und 12→6 wird die Anzahl der Indizes halbiert. Die Steifigkeitsmatrix C mit den 21 unabhängigen Komponenten C_ij repräsentiert den Elastizitätstensor des Materials.

Da die Inverse der Steifigkeitsmatrix, die sogenannte Nachgiebigkeitsmatrix, ebenfalls voll besetzt ist wie die Steifigkeitsmatrix, ist ersichtlich, dass jede Spannungskomponente für sich einen vollbesetzten Verzerrungstensor verursacht.

Materialparameter

Die Koeffizienten C_ij der Steifigkeitsmatrix haben die Dimension von Kraft pro Fläche und sind Parameter des Materials. Die Materialparameter können nicht beliebig gewählt werden, sondern müssen gewissen Stabilitätskriterien genügen. Diese folgen aus der Forderung, dass die Steifigkeits- und Nachgiebigkeitsmatrizen positiv definit sein müssen.

Notwendig dafür ist:

Alle Diagonalelemente der Steifigkeits- und Nachgiebigkeitsmatrix müssen positiv sein (damit sich das Material in Zugrichtung streckt, wenn man daran zieht, und nicht staucht) und
die Determinante der Steifigkeits- und Nachgiebigkeitsmatrix muss positiv sein (damit es unter Druck komprimiert und nicht expandiert).

Notwendig und hinreichend ist, das alle sechs Eigenwerte der Steifigkeitsmatrix positiv sind, denn dann sind es die der Nachgiebigkeitsmatrix ebenfalls.

Werden an einem realen Werkstoff Materialparameter identifiziert, die diesen Stabilitätskriterien widersprechen, ist Vorsicht geboten.

Hydrostatischer Spannungszustand und Kompressibilität

Der hydrostatische Spannungszustand stellt sich in einem allseitigem Druck ausgesetzten Körper ein. Wegen des auf der Erdoberfläche allgegenwärtigen Luftdrucks, ist dieser Zustand dort überall präsent. Wenn ein Körper aus kompressiblem isotropem Material allseitigem Druck ausgesetzt wird, dann schrumpft er in allen Raumrichtungen gleichermaßen. Ein kompressibles triklin anisotropes Material schrumpft in jeder Raumrichtung unterschiedlich und wird dabei geschert.

Das ist am einfachsten mit der Nachgiebigkeitsmatrix S in Voigt’scher Notation nachzuweisen:

{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\varepsilon _{4}\\\varepsilon _{5}\\\varepsilon _{6}\\\end{bmatrix}}={\begin{bmatrix}S_{11}&S_{12}&S_{13}&S_{14}&S_{15}&S_{16}\\S_{12}&S_{22}&S_{23}&S_{24}&S_{25}&S_{26}\\S_{13}&S_{23}&S_{33}&S_{34}&S_{35}&S_{36}\\S_{14}&S_{24}&S_{34}&S_{44}&S_{45}&S_{46}\\S_{15}&S_{25}&S_{35}&S_{45}&S_{55}&S_{56}\\S_{16}&S_{26}&S_{36}&S_{46}&S_{56}&S_{66}\end{bmatrix}}{\begin{bmatrix}-p\\-p\\-p\\0\\0\\0\end{bmatrix}}=-p{\begin{bmatrix}S_{11}+S_{12}+S_{13}\\S_{12}+S_{22}+S_{23}\\S_{13}+S_{23}+S_{33}\\S_{14}+S_{24}+S_{34}\\S_{15}+S_{25}+S_{35}\\S_{16}+S_{26}+S_{36}\end{bmatrix}}

Darin ist p der Druck. Beim triklin anisotropen linear elastischen Werkstoff kommt es bei allseitigem Druck zu Scherungen

{\begin{aligned}\gamma _{23}:=&2\varepsilon _{23}:=\varepsilon _{4}=-p(S_{14}+S_{24}+S_{34})\\\gamma _{13}:=&2\varepsilon _{13}:=\varepsilon _{5}=-p(S_{15}+S_{25}+S_{35})\\\gamma _{12}:=&2\varepsilon _{12}:=\varepsilon _{6}=-p(S_{16}+S_{26}+S_{36})\end{aligned}}

in allen Raumebenen, eine Eigenschaft, die keine andere real existierende Form der Anisotropie aufweist.

Die Kompression wird von den oberen drei Einträgen im rechten Vektor repräsentiert und wenn deren Summe verschwindet, dann zeigt

\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3}=\varepsilon _{\mathsf {v}}:={\frac {\mathrm {\mathsf {v}} -V}{V}}=-p[S_{11}+S_{22}+S_{33}+2(S_{23}+S_{13}+S_{12})]=0

dass das Material in erster Näherung inkompressibel ist, denn die Summe der Normaldehnungen ist die Volumendehnung ε_v, siehe Deviator#Deviatoren und Volumendehnung. Darin ist V das Volumen bei p=0 und v dasjenige beim aktuellen Druck. Bei kompressiblem Material ergibt sich der Kompressionsmodul K aus dem Kehrwert:[3]^:146

K:=-{\frac {\mathrm {d} p}{\frac {\mathrm {d} \mathrm {v} }{V}}}={\frac {1}{S_{11}+S_{22}+S_{33}+2(S_{23}+S_{13}+S_{12})}}

Beim triklin anisotropen, linear elastischen Werkstoff kontrahiert das Material in allen Raumrichtungen unterschiedlich, was die lineare Kompressibilität[3]^:146

{\displaystyle {\begin{aligned}\beta

ausdrückt. Hier sind n_1,2,3 die Koordinaten des Einheitsvektors ${\hat {n}}$ bezüglich der #körperfesten Basisvektoren.

Richtungsabhängigkeit des Elastizitätsmoduls

Der Elastizitätsmodul ist definiert als das Verhältnis der Spannung σ zur Dehnung ε bei reinem Zug:

E:={\frac {\sigma }{\varepsilon }}

Bei anisotropem Werkstoff ist der Modul richtungsabhängig und ergibt sich in Richtung des Einheitsvektors ${\hat {n}}$ aus

E_{n}:={\frac {\sigma _{n}}{\varepsilon _{n}}}:={\frac {{\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}}}{{\hat {n}}\cdot {\boldsymbol {\varepsilon }}\cdot {\hat {n}}}}

Bei reinem Zug in Richtung ${\hat {n}}$ ist ${\boldsymbol {\sigma }}=\sigma _{n}{\hat {n}}\otimes {\hat {n}}$ oder in voigtscher Notation

[{\boldsymbol {\sigma }}]=\sigma _{n}{\begin{pmatrix}n_{1}^{2}&n_{2}^{2}&n_{3}^{2}&n_{2}n_{3}&n_{1}n_{3}&n_{1}n_{2}\end{pmatrix}}^{\top }

mit den Komponenten n_1,2,3 des Richtungsvektors. Mit der Nachgiebigkeitsmatrix S werden daraus die Verzerrungen und der Verzerrungstensor berechnet mit dem Ergebnis[3]^:144

{\begin{aligned}E_{n}=&{\Big \{}\;\;S_{11}n_{1}^{4}+2n_{1}^{3}(S_{16}n_{2}+S_{15}n_{3})+n_{1}^{2}[S_{66}n_{2}^{2}+2(S_{14}+S_{56})n_{2}n_{3}+2S_{13}n_{3}^{2}]\\&+S_{22}n_{2}^{4}+2n_{2}^{3}(S_{24}n_{3}+S_{26}n_{1})+n_{2}^{2}[S_{44}n_{3}^{2}+2(S_{25}+S_{46})n_{1}n_{3}+2S_{12}n_{1}^{2}]\\&+S_{33}n_{3}^{4}+2n_{3}^{3}(S_{35}n_{1}+S_{34}n_{2})+n_{3}^{2}[S_{55}n_{1}^{2}+2(S_{36}+S_{45})n_{1}n_{2}+2S_{23}n_{2}^{2}]{\Big \}}^{-1}\end{aligned}}

Herleitung

In der Hyperelastizität ergeben sich die Spannungen aus der Ableitung der Formänderungsenergie nach den Dehnungen. Damit die Spannungen linear in den Dehnungen sind, muss demnach die Formänderungsenergie quadratisch in den Dehnungen sein, denn nur dann ist ihre Ableitung linear. Unter Verwendung der #Invarianten ergibt sich der Ansatz

{\begin{aligned}w({\boldsymbol {\varepsilon }}):=&{\frac {a}{2}}\varepsilon _{11}^{2}+{\frac {b}{2}}\varepsilon _{22}^{2}+{\frac {c}{2}}\varepsilon _{33}^{2}+2d\varepsilon _{23}^{2}+2e\varepsilon _{13}^{2}+2f\varepsilon _{12}^{2}+g\varepsilon _{11}\varepsilon _{22}+h\varepsilon _{11}\varepsilon _{33}+k\varepsilon _{22}\varepsilon _{33}\\&+2m\varepsilon _{11}\varepsilon _{23}+2n\varepsilon _{11}\varepsilon _{13}+2q\varepsilon _{11}\varepsilon _{12}+2r\varepsilon _{22}\varepsilon _{23}+2s\varepsilon _{22}\varepsilon _{13}+2t\varepsilon _{22}\varepsilon _{12}\\&+2u\varepsilon _{33}\varepsilon _{23}+2v\varepsilon _{33}\varepsilon _{13}+2w\varepsilon _{33}\varepsilon _{12}+4x\varepsilon _{23}\varepsilon _{13}+4y\varepsilon _{23}\varepsilon _{12}+4z\varepsilon _{13}\varepsilon _{12}\end{aligned}}

mit 21 Parametern a bis z. Nicht-linear hyperelastisches Verhalten kann modelliert werden, indem die Parameter a bis z durch Funktionen der Invarianten ersetzt werden.

Um die Formänderungsenergie nach ε ableiten zu können, müssen die Komponenten ε_ij als Funktion des Tensors ε ausgedrückt werden. Dies gelingt mit der Darstellung des Frobenius-Skalarprodukts ":" als Spur:

\mathbf {A

Darin bedeutet "·" das Matrizenprodukt und das hochgestellte ⊤ eine Transponierung. Mit der Abkürzung $\mathbf {K} _{ij}={\tfrac {1}{2}}({\hat {e}}_{i}\otimes {\hat {e}}_{j}+{\hat {e}}_{j}\otimes {\hat {e}}_{i})$ für die symmetrisierten dyadischen Produkte ⊗ der #körperfesten Basisvektoren ê_1,2,3 ist dann[4]

\mathbf {K} _{ij}:{\boldsymbol {\varepsilon }}={\frac {1}{2}}(\varepsilon _{ij}+\varepsilon _{ji})=\varepsilon _{ij}\quad \rightarrow \quad {\frac {\mathrm {d} \varepsilon _{ij}}{\mathrm {d} {\boldsymbol {\varepsilon }}}}=\mathbf {K} _{ij}

Aus dem Ansatz der Formänderungsenergie berechnen sich die Spannungen zu

{\begin{aligned}{\boldsymbol {\sigma }}={\frac {\mathrm {d} w}{\mathrm {d} {\boldsymbol {\varepsilon }}}}=&a\varepsilon _{11}\mathbf {K} _{11}+b\varepsilon _{22}\mathbf {K} _{22}+c\varepsilon _{33}\mathbf {K} _{33}+4d\varepsilon _{23}\mathbf {K} _{23}+4e\varepsilon _{13}\mathbf {K} _{13}+4f\varepsilon _{12}\mathbf {K} _{12}\\&+g(\varepsilon _{11}\mathbf {K} _{22}+\varepsilon _{22}\mathbf {K} _{11})+h(\varepsilon _{11}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{11})+k(\varepsilon _{22}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{22})\\&+2m(\varepsilon _{23}\mathbf {K} _{11}+\varepsilon _{11}\mathbf {K} _{23})+2n(\varepsilon _{13}\mathbf {K} _{11}+\varepsilon _{11}\mathbf {K} _{13})+2q(\varepsilon _{12}\mathbf {K} _{11}+\varepsilon _{11}\mathbf {K} _{12})\\&+2r(\varepsilon _{23}\mathbf {K} _{22}+\varepsilon _{22}\mathbf {K} _{23})+2s(\varepsilon _{13}\mathbf {K} _{22}+\varepsilon _{22}\mathbf {K} _{13})+2t(\varepsilon _{12}\mathbf {K} _{22}+\varepsilon _{22}\mathbf {K} _{12})\\&+2u(\varepsilon _{23}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{23})+2v(\varepsilon _{13}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{13})+2w(\varepsilon _{12}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{12})\\&+4x(\varepsilon _{13}\mathbf {K} _{23}+\varepsilon _{23}\mathbf {K} _{13})+4y(\varepsilon _{12}\mathbf {K} _{23}+\varepsilon _{23}\mathbf {K} _{12})+4z(\varepsilon _{12}\mathbf {K} _{13}+\varepsilon _{13}\mathbf {K} _{12})\end{aligned}}

oder in Voigt-Notation im ê_1,2,3-System

{\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{23}\\\sigma _{13}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}a\varepsilon _{11}+g\varepsilon _{22}+h\varepsilon _{33}+2m\varepsilon _{23}+2n\varepsilon _{13}+2q\varepsilon _{12}\\g\varepsilon _{11}+b\varepsilon _{22}+k\varepsilon _{33}+2r\varepsilon _{23}+2s\varepsilon _{13}+2t\varepsilon _{12}\;\\h\varepsilon _{11}+k\varepsilon _{22}+c\varepsilon _{33}+2u\varepsilon _{23}+2v\varepsilon _{13}+2w\varepsilon _{12}\\m\varepsilon _{11}+r\varepsilon _{22}+u\varepsilon _{33}+2d\varepsilon _{23}+2x\varepsilon _{13}+2y\varepsilon _{12}\\n\varepsilon _{11}+s\varepsilon _{22}+v\varepsilon _{33}+2x\varepsilon _{23}+2e\varepsilon _{13}+2z\varepsilon _{12}\\q\varepsilon _{11}+t\varepsilon _{22}+w\varepsilon _{33}+2y\varepsilon _{23}+2z\varepsilon _{13}+2f\varepsilon _{12}\end{bmatrix}}={\begin{bmatrix}a&g&h&m&n&q\\g&b&k&r&s&t\\h&k&c&u&v&w\\m&r&u&d&x&y\\n&s&v&x&e&z\\q&t&w&y&z&f\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\2\varepsilon _{23}\\2\varepsilon _{13}\\2\varepsilon _{12}\end{bmatrix}}

Die Parameter lassen sich den Einträgen in der #Steifigkeitsmatrix direkt zuordnen. Ableitung der Spannungen nach den Dehnungen liefert den konstanten und symmetrischen Elastizitätstensor 4. Stufe:

{\begin{aligned}\mathbb {C

Die Voigt-Notation der Tensoren K_ij mit i≠j besitzen den Eintrag ½ an einer Stelle und sonst nur nullen. Mit den Definitionen V_i=K_ii für i=1,2,3 und V₄=2K₂₃, V₅=2K₁₃ sowie V₆=2K₁₂, deren Koeffizienten nur nullen und einsen sind, entsteht eine Darstellung des Elastizitätstensors, an der seine Voigt-Notation direkt ablesbar ist:

{\begin{aligned}\mathbb {C} =&\quad \;(\,a\mathbf {V} _{1}+g\mathbf {V} _{2}+h\mathbf {V} _{3}+m\mathbf {V} _{4}+n\mathbf {V} _{5}+\,q\mathbf {V} _{6})\otimes \mathbf {V} _{1}\\&+(\;g\mathbf {V} _{1}+b\mathbf {V} _{2}+k\mathbf {V} _{3}+\;\,r\mathbf {V} _{4}+\,s\mathbf {V} _{5}+\;t\mathbf {V} _{6})\otimes \mathbf {V} _{2}\\&+(\;h\mathbf {V} _{1}+k\mathbf {V} _{2}+c\mathbf {V} _{3}+\;u\mathbf {V} _{4}+\,v\mathbf {V} _{5}+w\mathbf {V} _{6})\otimes \mathbf {V} _{3}\\&+(m\mathbf {V} _{1}+r\mathbf {V} _{2}+u\mathbf {V} _{3}+\;d\mathbf {V} _{4}+x\mathbf {V} _{5}+\,y\mathbf {V} _{6})\otimes \mathbf {V} _{4}\\&+(\;n\mathbf {V} _{1}+s\mathbf {V} _{2}+v\mathbf {V} _{3}+\;x\mathbf {V} _{4}+e\mathbf {V} _{5}+\;z\mathbf {V} _{6})\otimes \mathbf {V} _{5}\\&+(\;q\mathbf {V} _{1}+\,t\mathbf {V} _{2}+w\mathbf {V} _{3}+\;y\mathbf {V} _{4}+z\mathbf {V} _{5}+f\mathbf {V} _{6})\otimes \mathbf {V} _{6}\end{aligned}}

Weitere Eigenschaften

Dieser Abschnitt behandelt Eigenschaften die Gegenstand der Mechanik, Elektrizitätslehre, Thermodynamik oder Kristalloptik sind.

Zur Notation: Die Komponenten von Vektoren und Tensoren beziehen sich immer auf die #körperfesten Basisvektoren ê_1,2,3, beispielsweise v_i= ${\vec {\mathsf {v}}}$ · ê_i wenn ${\vec {\mathsf {v}}}$ ein Vektor ist oder T_ij=ê_i · T · ê_j wenn T ein Tensor zweiter Stufe ist, und es gilt die einsteinsche Summenkonvention.

Gleichgewichtseigenschaften

Die Eigenschaften dieses Abschnitts beziehen sich auf Gleichgewichtslagen oder reversible Prozesse.

Elektrische Permittivität und magnetische Permeabilität

Die elektrische Permittivität und magnetische Permeabilität sind Materialeigenschaften, die die Kräfte bestimmen, die ein elektrisches oder magnetisches Feld auf einen Körper ausübt. Die elektrische Flussdichte oder dielektrische Verschiebung D_i ist in einem triklin anisotropen Stoff nicht parallel zur elektrischen Feldstärke E_i, weswegen der Zusammenhang in einem nicht zu starken Feld mit einem Tensor zweiter Stufe, dem Permittivitätstensor κ_ij, ausgedrückt wird:[3]^:68

D_i=κ_ij E_j

Die Schreibweise κ statt ε wurde hier gewählt, um eine Verwechslung mit der mechanischen Dehnung zu vermeiden. Der Permittivitätstensor ist symmetrisch, hat damit reelle Eigenwerte und paarweise orthogonale oder orthgonalisierbare Eigenvektoren, und er besitzt in der triklinen Anisotropie sechs unabhängige Komponenten.[3]^:69,296

Ähnliche Verhältnisse gelten in einem Magnetfeld; es ist nur die dielektrische Verschiebung durch die magnetische Flussdichte B_i, die elektrische Feldstärke durch die magnetische H_i und die Permittivität durch die magnetische Permeabilität μ_ij zu ersetzen:

B_i=μ_ij H_j

Auch der Permeabilitätstensor ist symmetrisch und besitzt in der triklinen Anisotropie sechs unabhängige Komponenten.[3]^:23,55,296

Thermodynamik

Mit den Werkzeugen der Thermodynamik können verschiedene Effekte wie elastische Verformung und Piezoelektrizität einheitlich dargestellt und in Beziehung gesetzt werden. Es werden nur kleine, reversible Zustandsänderungen betrachtet, bei denen die mechanischen Dehnungen ε_ij, die dielektrischen Verschiebungen D_i und die Entropie s ausschließlich und linear von den mechanischen Spannungen σ_ij, der elektrischen Feldstärke E_i und der Temperatur T abhängen.[3]^:170ff

Die Differenziale der abhängigen Größen berechnen sich zu

${\begin{aligned}\mathrm {d} \varepsilon _{ij}=&{\stackrel {\text{Elastizität}}{\underbrace {\left({\frac {\partial \varepsilon _{ij}}{\partial \sigma _{kl}}}\right)_{E,T}} _{S_{ijkl}}}}\mathrm {d} \sigma _{kl}+{\stackrel {\begin{array}{c}{\text{Inverser}}\\[-1ex]{\text{Piezoeffekt}}\end{array}}{\underbrace {\left({\frac {\partial \varepsilon _{ij}}{\partial E_{k}}}\right)_{\sigma ,T}} _{d_{kij}}}}\mathrm {d} E_{k}+{\stackrel {\begin{array}{c}{\text{Thermische}}\\[-1ex]{\text{Ausdehnung}}\end{array}}{\underbrace {\left({\frac {\partial \varepsilon _{ij}}{\partial T}}\right)_{\sigma ,E}} _{\alpha _{ij}}}}\mathrm {d} T\\\mathrm {d} D_{i}=&{\stackrel {\text{Piezoeffekt}}{\left({\frac {\partial D_{i}}{\partial \sigma _{kl}}}\right)_{E,T}\mathrm {d} \sigma _{kl}}}+{\stackrel {\text{Permittivität}}{\underbrace {\left({\frac {\partial D_{i}}{\partial E_{k}}}\right)_{\sigma ,T}} _{\kappa _{ik}}\mathrm {d} E_{k}}}+{\stackrel {\begin{array}{c}{\text{Pyro-}}\\[-1ex]{\text{elektrizität}}\end{array}}{\underbrace {\left({\frac {\partial D_{i}}{\partial T}}\right)_{\sigma ,E}} _{p_{i}}}}\mathrm {d} T\\\mathrm {d} s=&{\stackrel {\begin{array}{c}{\text{Piezokalorischer}}\\[-1ex]{\text{Effekt}}\end{array}}{\left({\frac {\partial s}{\partial \sigma _{kl}}}\right)_{E,T}\mathrm {d} \sigma _{kl}}}+{\stackrel {\begin{array}{c}{\text{Elektrokalorischer}}\\[-1ex]{\text{Effekt}}\end{array}}{\left({\frac {\partial s}{\partial E_{k}}}\right)_{\sigma ,T}\mathrm {d} E_{k}}}+{\stackrel {\begin{array}{c}{\text{Wärme-}}\\[-2ex]{\text{kapazität}}\end{array}}{\left({\frac {\partial s}{\partial T}}\right)_{\sigma ,E}\mathrm {d} T}}\end{aligned}}$		(*)

Die Indizes hinter den Klammern bedeuten, dass die Klammerausdrücke unter Konstanthaltung der aufgeführten Größen ausgewertet werden. Wegen der angenommenen Linearität sind die Klammerausdrücke konstant, und die insgesamt 13 Gleichungen (9 Verzerrungen, 3 dielektrische Verschiebungen und die Entropie) können in Matrizenform geschrieben werden, mit einer Systemmatrix, die, wie sich unten zeigt, symmetrisch ist. Durch Ausnutzung der Symmetrie des mechanischen Spannungs- und Verzerrungstensors kann die Systemmatrix auf eine 10×10-Matrix reduziert werden.

Dem ersten und zweiten Hauptsatz der Thermodynamik zufolge ist das Differenzial der inneren Energie[3]^:179

\mathrm {d} U=\sigma _{ij}\mathrm {d} \varepsilon _{ij}+E_{j}\mathrm {d} D_{j}+T\mathrm {d} s

Das Differenzial der Funktion

\phi =U-\sigma _{ij}\varepsilon _{ij}-E_{i}D_{i}-Ts

wird damit

\mathrm {d} \phi =-\varepsilon _{ij}\mathrm {d} \sigma _{ij}-D_{i}\mathrm {d} E_{i}-s\mathrm {d} T=\left({\frac {\partial \phi }{\partial \sigma _{ij}}}\right)_{E,T}\mathrm {d} \sigma _{ij}+\left({\frac {\partial \phi }{\partial E_{i}}}\right)_{\sigma ,T}\mathrm {d} E_{i}+\left({\frac {\partial \phi }{\partial T}}\right)_{\sigma ,E}\mathrm {d} T

Koeffizientenvergleich liefert

\left({\frac {\partial \phi }{\partial \sigma _{ij}}}\right)_{E,T}=-\varepsilon _{ij},\quad \left({\frac {\partial \phi }{\partial E_{i}}}\right)_{\sigma ,T}=-D_{i},\quad \left({\frac {\partial \phi }{\partial T}}\right)_{\sigma ,E}=-s

und nach dem Satz von Schwarz mit Gleichung (*)

{\begin{aligned}-\left({\frac {\partial ^{2}\phi }{\partial E_{k}\partial \sigma _{ij}}}\right)_{T}=&\left({\frac {\partial D_{k}}{\partial \sigma _{ij}}}\right)_{E,T}=\left({\frac {\partial \varepsilon _{ij}}{\partial E_{k}}}\right)_{\sigma ,T}=d_{kij}^{T}\\-\left({\frac {\partial ^{2}\phi }{\partial T\partial \sigma _{ij}}}\right)_{E}=&\left({\frac {\partial s}{\partial \sigma _{ij}}}\right)_{E,T}=\left({\frac {\partial \varepsilon _{ij}}{\partial T}}\right)_{\sigma ,E}=\alpha _{ij}^{E}\\-\left({\frac {\partial ^{2}\phi }{\partial T\partial E_{i}}}\right)_{\sigma }=&\left({\frac {\partial s}{\partial E_{i}}}\right)_{\sigma ,T}=\left({\frac {\partial D_{i}}{\partial T}}\right)_{\sigma ,E}=p_{i}^{\sigma }\end{aligned}}

Dies zeigt:[3]^:180

Die oben erwähnte Systemmatrix von Gleichung (*) ist symmetrisch.
Die Koeffizienten des inversen Piezoeffekts sind gleich denen des direkten Effekts.
Die Koeffizienten für die thermische Ausdehnung sind gleich denen für den piezokalorischen Effekt.
Die Koeffizienten für den pyroelektrischen Effekt sind gleich denen für den elektrokalorischen Effekt.

Thermo- und Elektromechanische Gleichgewichtseigenschaften

Das trikline Kristallsystem umfasst die beiden Kristallklassen (Punktgruppen), die in den Tabellen aufgeführt sind.

Kristallsystem

Triklin

Kristallklasse¹, ¹=[2]^:33

1

Hermann-Mauguin-Symbol¹

1

#Symmetriegruppe¹

\{\mathbf {1} \}

Gruppenordnung¹

1

Systemmatrix:[3]^:296

	σ₁	σ₂	σ₃	σ₄	σ₅	σ₆	E₁	E₂	E₃	𝚫T
ε₁	S₁₁	S₁₂	S₁₃	S₁₄	S₁₅	S₁₆	d₁₁	d₂₁	d₃₁	α₁
ε₂	S₁₂	S₂₂	S₂₃	S₂₄	S₂₅	S₂₆	d₁₂	d₂₂	d₃₂	α₂
ε₃	S₁₃	S₂₃	S₃₃	S₃₄	S₃₅	S₃₆	d₁₃	d₂₃	d₃₃	α₃
ε₄	S₁₄	S₂₄	S₃₄	S₄₄	S₄₅	S₄₆	d₁₄	d₂₄	d₃₄	α₄
ε₅	S₁₅	S₂₅	S₃₅	S₄₅	S₅₅	S₅₆	d₁₅	d₂₅	d₃₅	α₅
ε₆	S₁₆	S₂₆	S₃₆	S₄₆	S₅₆	S₆₆	d₁₆	d₂₆	d₃₆	α₆
D₁	d₁₁	d₁₂	d₁₃	d₁₄	d₁₅	d₁₆	κ₁₁	κ₁₂	κ₁₃	p₁
D₂	d₂₁	d₂₂	d₂₃	d₂₄	d₂₅	d₂₆	κ₁₂	κ₂₂	κ₂₃	p₂
D₃	d₃₁	d₃₂	d₃₃	d₃₄	d₃₅	d₃₆	κ₁₃	κ₂₃	κ₃₃	p₃
𝚫s	α₁	α₂	α₃	α₄	α₅	α₆	p₁	p₂	p₃	c_σ/T

Kristallsystem

Triklin

Kristallklasse¹, ¹=[2]^:33

2

Hermann-Mauguin-Symbol¹

1

#Symmetriegruppe¹

\{-\mathbf {1} ,\mathbf {1} \}

Gruppenordnung¹

2

Systemmatrix:[3]^:296

	σ₁	σ₂	σ₃	σ₄	σ₅	σ₆	E₁	E₂	E₃	𝚫T
ε₁	S₁₁	S₁₂	S₁₃	S₁₄	S₁₅	S₁₆	·	·	·	α₁
ε₂	S₁₂	S₂₂	S₂₃	S₂₄	S₂₅	S₂₆	·	·	·	α₂
ε₃	S₁₃	S₂₃	S₃₃	S₃₄	S₃₅	S₃₆	·	·	·	α₃
ε₄	S₁₄	S₂₄	S₃₄	S₄₄	S₄₅	S₄₆	·	·	·	α₄
ε₅	S₁₅	S₂₅	S₃₅	S₄₅	S₅₅	S₅₆	·	·	·	α₅
ε₆	S₁₆	S₂₆	S₃₆	S₄₆	S₅₆	S₆₆	·	·	·	α₆
D₁	·	·	·	·	·	·	κ₁₁	κ₁₂	κ₁₃	·
D₂	·	·	·	·	·	·	κ₁₂	κ₂₂	κ₂₃	·
D₃	·	·	·	·	·	·	κ₁₃	κ₂₃	κ₃₃	·
𝚫s	α₁	α₂	α₃	α₄	α₅	α₆	·	·	·	c_σ/T

Die Symmetriegruppe 2 gehört zu den elf mechanischen Symmetriegruppen oder Anisotropietypen, bei denen die Lage der Atome oder Moleküle in der Elementarzelle die Symmetrien des Kristallgitters widerspiegelt, und sie enthält die Punktspiegelung -1.[2]^:35

Die Systemmatrix der physikalischen Eigenschaften ist symmetrisch, siehe #Thermodynamik, und erfasst hier nur die linearen Effekte einer Theorie erster Ordnung. Der zehnparametrige Zustandsvektor enthält die mechanischen Spannungen σ_k, die Elektrische Feldstärke E_j und die Temperaturdifferenz 𝚫T. Sie verursachen Dehnungen ε_k, dielektrische Verschiebungen D_j und Entropieänderungen 𝚫s, was hier klein geschrieben wird, um eine Verwechselung mit den Koeffizienten der Nachgiebigkeitsmatrix zu vermeiden. Die Matrix gibt die Kopplungsgrößen an, wobei die Punkte · für nullen stehen. In der ersten Kristallklasse beschreiben 55, in der zweiten 34 Parameter alle hier aufgeführten, linearisierten, physikalischen Effekte.

Die Gleichungen werden unten in Voigtscher Indexnotation geschrieben. Bei den piezoelektrischen Verzerrungskoeffizienten d_ik, den Ausdehnungskoeffizient α_k, den Verzerrungen ε_k und Spannungen σ_k sind für k die Zuordnungen 1→11, 2→22, 3→33, 4→23, 5→13, 6→12 zu beachten, die bei den Nachgiebigkeitskoeffizienten S_jk auf beide Indizies anwendbar sind.[3]^:180

Elastizität (Physik): Die Nachgiebigkeitsmatrix mit Koeffizienten S_jk vermittelt zwischen Spannungen und Dehnungen, wie im Abschnitt #Triklin anisotrope lineare Elastizität dargelegt: ε_j=S_jk σ_k
Inverser Piezoeffekt: Anlegen einer elektrischen Spannung bewirkt eine Verformung: ε_k=E_j d_jk gemäß den piezoelektrischen Verzerrungskoeffizienten d_jk. Dieser Effekt ist nur in der ersten Kristallklasse zu beobachten.
Thermische Ausdehnung: Eine Temperaturerhöhung lässt das Material sich in allen Raumrichtungen ausdehnen: ε_k=α_k 𝚫T[3]^:176 Die Ausdehnungskoeffizienten sind die Koeffizienten eines symmetrischen Tensors zweiter Stufe. Eine Temperaturänderung bewirkt neben Normaldehnungen auch Schubverzerrungen.
Piezoeffekt: Eine mechanische Spannung erzeugt eine dielektrische Verschiebung D_j=d_jk σ_k, was nur in der ersten Kristallklasse möglich ist.
Permittivität: Eine angelegte elektrischen Feldstärke E_i bewirkt mit der Permittivität κ_ij eine dielektrische Verschiebung D_i=κ_ij E_j.
Pyroelektrischer Effekt: Eine Temperaturänderung 𝚫T bewirkt eine dielektrische Verschiebung D_i=p_i 𝚫T mit der pyroelektrischen Konstante p_i, die in der zweiten Kristallklasse null ist, d. h. der Effekt tritt dort nicht auf.
Entropieänderung: Eine Entropieänderung wird durch mechanische und elektrische Spannungen sowie eine Temperaturänderung erzeugt: 𝚫s=α_k σ_k+p_i E_i+(c_σ/T) 𝚫T, wobei c_σ die spezifische Wärmekapazität bei konstanter mechanischer Spannung ist.[3]^:176 In der zweiten Kristallklasse trägt die elektrische Spannung wegen p_1,2,3=0 nichts dazu bei.

Transport-Eigenschaften

Bei den Eigenschaften in diesem Abschnitt geht es um Transport von Wärme oder elektrischer Ladung, Prozesse die mit Dissipation und Irreversibilität zu tun haben.

Wärmeleitfähigkeit

In der triklinen Anisotropie ist die Wärmestromdichte ${\dot {\vec {q}}}$ nicht – wie in isotropen Medien – antiparallel zum Temperaturgradient grad T, weshalb für die Wärmeleitfähigkeit λ ein Wärmeleitfähigkeitstensor λ einzusetzen ist:[3]^:195

{\dot {\vec {q}}}=-{\boldsymbol {\lambda }}\cdot \mathrm {grad} \,T

Der Wärmeleitfähigkeitstensor ist symmetrisch und in der triklinen Anisotropie voll besetzt.[3]^:195

Das Onsagersche Prinzip führt zwar nur darauf, dass die Divergenz des schiefsymmetrischen Anteils div(λ-λ^⊤) den Nullvektor ergibt, λ also durchaus schiefsymmetrisch sein kann (das hochgestellte „⊤“ bedeutet eine Transponierung). Da dies aber erstens zu keinen messbaren Effekten führt und zweitens die Konsequenz hätte, dass das Vakuum eine nicht verschwindende Wärmeleitfähigkeit besitzen müsste, ist die Annahme der Symmetrie zwar nicht erzwungen, so doch statthaft.[3]^:211

Spezifischer Widerstand

In der triklinen Anisotropie ist die Stromdichte J_i nicht – wie in isotropen Medien – parallel zur elektrischen Feldstärke E_i, weshalb sich der spezifische Widerstand ρ als Tensor zweiter Stufe darstellt:[3]^:204f

E_i=ρ_ik J_k

Die elektrische Leitfähigkeit σ ist dann ebenfalls ein Tensor:

J_i=σ_ik E_k

(nicht zu verwechseln mit dem mechanischen Spannungstensor.) Diese Tensoren sind symmetrisch und in der triklinen Anisotropie voll besetzt.

Thermoelektrizität

Die Thermoelektrizität wird im anisotropen Stoff mathematisch beschrieben durch die Gleichungen[3]^:225

{\begin{aligned}\mathrm {grad} \,{\bar {\mu }}=&-e^{2}{\boldsymbol {\rho }}\cdot {\vec {J}}^{e}-{\boldsymbol {\Sigma }}\cdot \mathrm {grad} \,T\\{\dot {\vec {q}}}=&T{\boldsymbol {\Sigma }}^{\top }\cdot {\vec {J}}^{e}-{\boldsymbol {\lambda }}\cdot \mathrm {grad} \,T\end{aligned}}

mit

dem elektrochemischen Potential μ des Elektrons,
der Ladung des Elektrons -e,
der Stromdichte ${\vec {J}}^{e}=-{\vec {J}}/e$ ,
dem thermoelektrischen Tensor Σ, der die thermoelektrischen Eigenschaften des Kristalls verkörpert,
dem spezifischen Widerstand ρ
dem Temperaturgradient grad T und
dem Wärmeleitfähigkeitstensor λ

Der thermoelektrische Tensor Σ ist unsymmetrisch und im triklinen Material voll besetzt.[3]^:227

Optische Eigenschaften

Bei den Eigenschaften in diesem Abschnitt geht es darum, wie durchsichtige Kristalle auf sie durchdringendes Licht wirken und wie das von äußeren Einflüssen abhängt. Allgemein lässt sich sagen:

“A crystal under an external influence will exhibit only those symmetry elements that are common to the crystal without the influence and the influence without the crystal”

„Ein Kristall unter äußerem Einfluss weist nur die Symmetrieelemente auf, die dem Kristall ohne Einfluss und dem Einfluss ohne den Kristall gemeinsam sind“

– John Nye[3]^:245

Ein äußerer Einfluss vermag die Symmetrieeigenschaften eines Kristalls nur zu verringern. Wenn ein dem Kristall (ohne Einfluss) und dem äußeren Einfluss (bevor er auf das Kristall angewendet wird) gemeinsames Symmetrieelement auf das Kristall und den äußeren Einfluss angewendet wird, dann wird sich bei beiden keine Veränderung zeigen.

Doppelbrechung

Der Brechungsindex ist eine Materialeigenschaft, die nach dem snelliusschen Brechungsgesetz angibt, wie groß die Richtungsänderung eines Lichtstrahls beim Durchtritt durch ein transparentes Kristall sein wird. Der Brechungsindex lässt sich anschaulich aus dem Indexellipsoid ableiten, dessen Halbachsen erstens parallel zu den Eigenvektoren der dielektrischen Moduln η_ij ausgerichtet und deren Länge zweitens eine Funktion der entsprechenden Eigenwerte sind. Die dielektrischen Moduln sind an denselben Stellen besetzt wie die Permittivität κ_ij und daher wie sie symmetrisch (η_ij=η_ji). Triklin anisotrope Stoffe sind optisch zweiachsig, denn sie besitzen sechs unabhängige dielektrische Moduln.[3]^:296 Ferner beeinflussen mechanische und elektrische Spannungen die Moduln, siehe #Photoelastischer und elektrooptischer Effekt.

Photoelastischer und elektrooptischer Effekt

Die dielektrischen Moduln, siehe #Doppelbrechung, werden von der elektrischen Feldstärke E_k und von mechanischen Spannungen σ_kl beeinflusst:

𝚫η_ij=z_ijk E_k + π_ijkl σ_kl

Die z_ijk werden elektro-optische und die π_ijkl piezo-optische Koeffizienten genannt.[3]^:244 Ein einachsiger Zug oder ein elektrisches Feld ergibt auf diese Weise ein optisch zweiachsiges Kristall.[3]^:246 Die η_ij sind aus den gleichen Gründen symmetrisch (η_ij=η_ji) wie die Permittivität κ_ij, siehe #Thermodynamik. Von den 27 möglichen elektro-optischen Koeffizienten sind daher nur 18 unabhängig, genauso viele wie piezoelektrische Verzerrungskoeffizienten d_ijk, siehe #Thermo- und Elektromechanische Gleichgewichtseigenschaften. Der elektro-optische Effekt tritt daher nur in der ersten und nicht in der zweiten Kristallklasse auf.

Weil der mechanische Spannungstensor σ_ij symmetrisch ist, sind von den 3⁴=81 piezo-optischen Koeffizienten nur 36 unabhängig (wegen π_ijkl=π_ijlk=π_jikl.) Diese Anzahl wird in der triklinen Anisotropie für die Beschreibung der optischen Elastizität gebraucht, weil keine weiteren Symmetrien auftreten.[3]^:250

Optische Aktivität

Die optische Aktivität bezeichnet die Eigenschaft durchsichtiger Materialien die Polarisationsrichtung des durchdringenden Lichts zu drehen. Der Drehwinkel ist[3]^:262,266

\phi ={\frac {\pi d}{\lambda _{0}{\bar {n}}}}({\hat {k}}\cdot \mathbf {g} \cdot {\hat {k}})

mit

der Wellenlänge im Vakkum λ₀,
dem Brechungsindex n auf der optischen Achse,
dem Wellenvektor ${\hat {k}}$ ,
dem symmetrischen Drehtensor (englisch gyration tensor)[3]^:272 zweiter Stufe g und
der Distanz d, die das Licht im Kristall zurücklegt.

Ein Kristall, dessen #Symmetriegruppe die Punktspiegelung -1 enthält, kann nicht optisch aktiv sein[3]^:271, und daher ist in der zweiten Kristallklasse g=0. Im triklin anisotropen Material der ersten Kristallklasse besitzt der Drehtensor sechs unabhängige Komponenten.

Siehe auch

Hookesches Gesetz für isotrope lineare Elastizität
Monokline Anisotropie
Hexagonale Anisotropie
Tetragonale Anisotropie
Kubische Anisotropie
Transversale Isotropie
Materialmodell
Spezielle lineare Gruppe

Einzelnachweise und Fußnoten

P. Haupt: Kontinuumsmechanik und Materialtheorie. 2002.
Nikolas Apel: Ansätze zur Beschreibung des anisotropen Materialverhaltens bei finiten elastischen und plastischen Verformungen. Theorie und Numerik. 2004.
J.F. Nye: Physikalische Eigenschaften von Kristallen. Ihre Representation durch Tensoren und Matrizen. 1985.
Die ij-Komponente eines beliebigen Tensors zweiter Stufe T im ê_1,2,3-System ist
${\begin{aligned}T_{ij}:=&{\hat {e}}_{i}\cdot \mathbf {T} \cdot {\hat {e}}_{j}={\hat {e}}_{j}\cdot ({\hat {e}}_{i}\cdot \mathbf {T} )\\=&\mathrm {Spur} ({\hat {e}}_{j}\otimes {\hat {e}}_{i}\cdot \mathbf {T} ):=({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {T} \end{aligned}}$
Die Fréchet-Ableitung hiervon nach T ist der beschränkte lineare Operator ${\mathcal {A}}$ der – sofern er existiert – in allen Richtungen H dem Gâteaux-Differenzial entspricht, also
${\begin{aligned}{\mathcal {A}}(\mathbf {H} )=&\left.{\frac {\mathrm {d} }{\mathrm {d} s}}[({\hat {e}}_{i}\otimes {\hat {e}}_{j}):(\mathbf {T} +s\mathbf {H} )]\right|_{s=0}\\=&({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} \quad \forall \;\mathbf {H} \end{aligned}}$
Darin ist $s\in \mathbb {R}$ und der lineare Operator ist das Skalarprodukt mit ${\hat {e}}_{i}\otimes {\hat {e}}_{j}$ . Hier ist $\mathbf {T} ={\boldsymbol {\varepsilon }}$ ein symmetrischer Tensor, dessen Differenzial H auch symmetrisch ist. Beim Skalarprodukt mit diesem trägt nur der symmetrische Anteil etwas bei:
$({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} ={\frac {1}{2}}({\hat {e}}_{i}\otimes {\hat {e}}_{j}+{\hat {e}}_{j}\otimes {\hat {e}}_{i}):\mathbf {H} =\mathbf {K} _{ij}:\mathbf {H}$
wo nun H auch unsymmetrisch sein kann. Dann wird auch
${\mathcal {A}}={\frac {\partial T_{ij}}{\partial \mathbf {T} }}=\mathbf {K} _{ij}$
geschrieben.

Literatur

J. Betten: Kontinuumsmechanik – Elastisches und inelastisches Verhalten isotroper und anisotroper Stoffe. Springer, 2012, ISBN 3-642-62645-9.
Nikolas Apel: Ansätze zur Beschreibung des anisotropen Materialverhaltens bei finiten elastischen und plastischen Verformungen. Theorie und Numerik. Hrsg.: Universität Stuttgart. OPUS – Online Publikationen der Universität Stuttgart, Stuttgart 2004, ISBN 3-937859-00-4 (englisch, researchgate.net [abgerufen am 28. Oktober 2021] Originaltitel: Approaches to the Description of Anisotropic Material Behaviour at Finite Elastic and Plastic Deformations – Theory and Numerics.).
P. Haupt: Kontinuumsmechanik und Materialtheorie. Springer, 2002, ISBN 978-3-642-07718-0, doi:10.1007/978-3-662-04775-0 (englisch, Originaltitel: Continuum Mechanics and Theory of Materials.).
R. E. Newnham: Eigenschaften von Materialien. Oxford University Press, 2005, ISBN 978-0-19-852075-7 (englisch, Originaltitel: Properties of materials.).
J.F. Nye: Physikalische Eigenschaften von Kristallen. Ihre Representation durch Tensoren und Matrizen. Oxford University Press, 1985, ISBN 978-0-19-851165-6 (englisch, Originaltitel: Physical Properties of Crystals: Their Representation by Tensors and Matrices.).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[haupt-1] P. Haupt: Kontinuumsmechanik und Materialtheorie. 2002.

[apel-2] Nikolas Apel: Ansätze zur Beschreibung des anisotropen Materialverhaltens bei finiten elastischen und plastischen Verformungen. Theorie und Numerik. 2004.

[nye-3] J.F. Nye: Physikalische Eigenschaften von Kristallen. Ihre Representation durch Tensoren und Matrizen. 1985.

[Frechet-4] Die ij-Komponente eines beliebigen Tensors zweiter Stufe T im ê_1,2,3-System ist
${\begin{aligned}T_{ij}:=&{\hat {e}}_{i}\cdot \mathbf {T} \cdot {\hat {e}}_{j}={\hat {e}}_{j}\cdot ({\hat {e}}_{i}\cdot \mathbf {T} )\\=&\mathrm {Spur} ({\hat {e}}_{j}\otimes {\hat {e}}_{i}\cdot \mathbf {T} ):=({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {T} \end{aligned}}$
Die Fréchet-Ableitung hiervon nach T ist der beschränkte lineare Operator ${\mathcal {A}}$ der – sofern er existiert – in allen Richtungen H dem Gâteaux-Differenzial entspricht, also
${\begin{aligned}{\mathcal {A}}(\mathbf {H} )=&\left.{\frac {\mathrm {d} }{\mathrm {d} s}}[({\hat {e}}_{i}\otimes {\hat {e}}_{j}):(\mathbf {T} +s\mathbf {H} )]\right|_{s=0}\\=&({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} \quad \forall \;\mathbf {H} \end{aligned}}$
Darin ist $s\in \mathbb {R}$ und der lineare Operator ist das Skalarprodukt mit ${\hat {e}}_{i}\otimes {\hat {e}}_{j}$ . Hier ist $\mathbf {T} ={\boldsymbol {\varepsilon }}$ ein symmetrischer Tensor, dessen Differenzial H auch symmetrisch ist. Beim Skalarprodukt mit diesem trägt nur der symmetrische Anteil etwas bei:
$({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} ={\frac {1}{2}}({\hat {e}}_{i}\otimes {\hat {e}}_{j}+{\hat {e}}_{j}\otimes {\hat {e}}_{i}):\mathbf {H} =\mathbf {K} _{ij}:\mathbf {H}$
wo nun H auch unsymmetrisch sein kann. Dann wird auch
${\mathcal {A}}={\frac {\partial T_{ij}}{\partial \mathbf {T} }}=\mathbf {K} _{ij}$
geschrieben.