Monokline Anisotropie

Die monokline Anisotropie (von altgriechisch μόνος mónos „allein“, „einzig“ und κλίνειν klinein „neigen“, „beugen“), gehörend zum gleichnamigen Kristallsystem, ist eine spezielle Art der Richtungsabhängigkeit eines Werkstoffs/Materials.

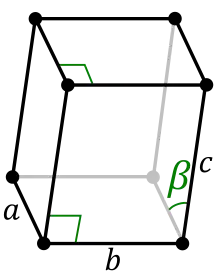
Bravais-Gitter eines monoklin anisotropen Kristalls (a≠b≠c, β≠90°)

Monokline Materialien wie im Bild haben die folgenden Eigenschaften:

Das Kraft-Verformungs-Verhalten ändert sich nicht, wenn das Material um 180 Grad auf der Grundebene gedreht wird, die die Seiten a und b enthält.
Bei reinem Zug in der Grundebene (in a- oder b-Richtung) kommt es zu Schubverzerrungen in der Grundebene.
Scherungen senkrecht zur Grundebene (ac oder bc enthaltend) sind gekoppelt.

Ein monoklin anisotropes linear elastisches Material besitzt maximal 13 Materialparameter.

Ein Material ist isotrop, wenn es richtungsunabhängig dasselbe Kraft-Verformungs-Verhalten hat. Bei anisotropen Materialien ist das Kraft-Verformungs-Verhalten von der Belastungsrichtung abhängig. Die monokline Anisotropie ist ein Spezialfall der triklinen Anisotropie und enthält ihrerseits die Tetragonale Anisotropie und Orthotropie als Sonderfall (β=90°, siehe Bild).[1]^{:381 f.}

Feldspate gelten als die wichtigsten gesteinsbildenden Minerale der Erdkruste und kristallieren monoklin oder triklin. Einige als Elektrodenmaterial für Lithium-Ionen-Akkumulatoren geeignete Materialien,[2] Zirkoniumdioxid (m-ZrO₂)[3] und Gips, sind technisch bedeutsame monoklin anisotrope Werkstoffe. Kristalle des monoklinen Kristallsystems, mit einer Elementarzelle wie im Bild, sind monoklin anisotrop.

Symmetriegruppe

Die Richtungsabhängigkeit eines Materials zeichnet sich dadurch aus, dass das Kraft-Verformungs-Verhalten unabhängig (invariant) ist gegenüber nur bestimmten Drehungen des Materials. Diese Drehungen bilden zusammen mit der Punktspiegelung die Symmetriegruppe des Materials.[1]^:381

Das monokline Material besitzt eine Symmetrieebene, in der 180-Grad-Drehungen keinen Einfluss auf das Materialverhalten haben. Diese Ebene wird üblicherweise durch die ersten beiden Basisvektoren ê_1,2 eines Orthonormalsystems aufgespannt; die 3-Richtung ê₃, um die mit 180° gedreht wird, ist dazu senkrecht. Die Vektoren ê_1,2,3 werden im Folgenden Strukturvektoren genannt, weil sie die Struktur des Materials beschreiben.

Die Invarianz gegenüber der Drehung um die 3-Achse veranschaulichen zwei Experimente an einem Teilchen: Im ersten Experiment bringt man am Teilchen eine bestimmte Kraft auf und misst die resultierende Verformung. Im zweiten Experiment dreht man das Material um 180 Grad um die 3-Achse. Dann bringt man dieselbe Kraft auf wie im ersten Experiment und misst erneut die Verformung. Bei monoklinem Material wird man im zweiten Experiment dieselbe Verformung messen wie im ersten. Und zwar auch bei nicht-linear elastischem Materialverhalten.

Die Abhängigkeit von den Transformationen des Materials erkennt man, wenn man im zweiten Experiment um einen anderen Winkel als 180 Grad oder um eine andere als die 3-Richtung dreht. Wenn nicht einer der #Spezialfälle der monoklinen Anisotropie vorliegt, wird man nun immer eine andere Verformung messen als im ersten Experiment.

Die angesprochenen Transformationen werden in der Kontinuumsmechanik durch orthogonale Tensoren Q repräsentiert. Eine Symmetriegruppe g_R besteht aus denjenigen Transformationen, die die Formänderungsenergie w invariant lassen. Mathematisch wird das mit dem Verzerrungstensor E durch

\mathbf {Q} \in g_{R}\quad \leftrightarrow \quad w(\mathbf {Q\cdot E\cdot Q} ^{\top })=w(\mathbf {E} )

für alle E

ausgedrückt.[1]^:379 Darin bedeutet „·“ das Matrizenprodukt und das hochgestellte „⊤“ eine Transponierung. Mit Q gehört auch -Q zur Symmetriegruppe, was durch Hinzufügen des negativen Einheitstensors -1, der eine Punktspiegelung repräsentiert, zu g_R berücksichtigt wird. Die Symmetriegruppe des monoklinen Materials ist[1]^:382

g_{R}=\left\{-\mathbf {1} ,\mathbf {Q} _{3}^{\pi }\right\}

mit Gruppenordnung=4

Darin steht $\mathbf {Q} _{3}^{\alpha }$ für den orthogonalen Tensor, der mit dem Winkel α in Radiant um die 3-Achse dreht.

Invarianten

In der isotropen Hyperelastizität hängt die Formänderungsenergie von den Hauptinvarianten I_1,2,3 des Verzerrungstensors E ab:

w(E)=w(I₁, I₂, I₃)

Die analoge Darstellung der Anisotropie erfordert, dass ein komplettes System von skalarwertigen Funktionen bekannt ist, die unter allen Transformationen in der Symmetriegruppe g_R invariant sind.[1]^:380 In der monoklinen Anisotropie sind die folgenden Terme Invarianten:[1]^:381

E₁₁, E₂₂, E₃₃, E₁₂, E₁₃², E₂₃², E₁₃E₂₃.

Darin ist E_ij := ê_i·E·ê_j für i,j=1,2,3 und ê_1,2,3 sind die #Strukturvektoren.

Spezialfälle der monoklinen Anisotropie

Die monokline Anisotropie enthält die Hexagonale Anisotropie mit sechszähliger Symmetrie, Tetragonale Anisotropie und die Orthotropie als Spezialfälle.

Die Orthotropie enthält die Kubische Anisotropie, die Transversale Isotropie und Isotropie als Spezialfälle.

Nur die trikline und die Hexagonale Anisotropie mit dreizähliger Symmetrie weisen Formen der Anisotropie auf, die nicht in der monoklinen enthalten sind.

Monoklin anisotrope lineare Elastizität

Gegeben sind zwei Tensoren zweiter Stufe ${\boldsymbol {\sigma }}$ und ${\boldsymbol {\varepsilon }}$ mit 3×3-Koeffizienten $\sigma _{ij}$ bzw. $\varepsilon _{ij}$ . Der allgemeinste lineare Zusammenhang, den es zwischen diesen Koeffizienten gibt, ist:

f_{C}:\varepsilon _{kl}\rightarrow \sigma _{ij}=\sum _{k,l=1}^{3}C_{ijkl}\varepsilon _{kl}

.

Darin sind $C_{ijkl}$ 81 Koeffizienten mit denen die neun Komponenten $\varepsilon _{ij}$ auf neun Komponenten $\sigma _{ij}$ abgebildet werden. In der linearen Elastizitätstheorie, in der der symmetrische Spannungstensor ${\boldsymbol {\sigma }}$ eine lineare Funktion des ebenfalls symmetrischen Verzerrungstensors ${\boldsymbol {\varepsilon }}$ ist, reduziert sich die Anzahl der unabhängigen Tensor-Komponenten auf sechs, so dass nur 36 Koeffizienten unabhängig sind (wegen $C_{ijkl}=C_{jikl}=C_{ijlk}$ ). Die Hyperelastizität bewirkt die zusätzliche Symmetrie $C_{ijkl}=C_{klij}$ , sodass nur maximal 21 Koeffizienten ausreichen, um das Material zu beschreiben.

Der Zusammenhang zwischen Spannungen und Verzerrungen kann in Voigt’scher Notation auch als Matrizengleichung geschrieben werden. In einem monoklin anisotropen linear elastischen Material existiert eine Orthonormalbasis, die #Strukturvektoren ê_1,2,3, in der die Spannungs-Dehnungs-Beziehung die Form[1]^:390[4]^:637

{\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\\\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}&0&0&C_{16}\\C_{12}&C_{22}&C_{23}&0&0&C_{26}\\C_{13}&C_{23}&C_{33}&0&0&C_{36}\\0&0&0&C_{44}&C_{45}&0\\0&0&0&C_{45}&C_{55}&0\\C_{16}&C_{26}&C_{36}&0&0&C_{66}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\2\varepsilon _{4}\\2\varepsilon _{5}\\2\varepsilon _{6}\\\end{bmatrix}}

.

annimmt. Hier wurde mittels der Zuordnung 11→1, 22→2, 33→3, 23→4, 13→5 und 12→6 die Anzahl der Indizes halbiert. Die Steifigkeitsmatrix C mit den 13 unabhängigen Komponenten C_ij repräsentiert den Elastizitätstensor des Materials.

Da die Inverse der Steifigkeitsmatrix, die sogenannte Nachgiebigkeitsmatrix, an denselben Stellen besetzt ist wie die Steifigkeitsmatrix, ist ersichtlich, dass reiner Zug in 3-Richtung mit σ₃ ≠ 0, σ_i = 0 sonst, wie bei isotropen Materialien auch, Normaldehnungen in den anderen Raumrichtungen hervorruft. Zusätzlich bewirkt hier der reine Zug in 3-Richtung eine Schubverzerrung in der 12-Ebene, was die monokline Anisotropie von der Orthotropie und ihren Spezialfällen unterscheidet. Ein weiterer Unterschied ist, dass eine Schubspannung in der 23-Ebene neben Schubverzerrungen in derselben Ebene auch solche in der 13-Ebene bewirken.

Wenn die vierte und sechste Zeile und Spalte vertauscht werden,[1]^:390 kann die Steifigkeitsmatrix in eine 4×4- und eine 2×2-Untermatrix aufgeteilt werden, was bei der Berechnung der Determinante, der Nachgiebigkeitsmatrix und der Eigenwerte[4]^:637 hilfreich ist.

Materialparameter

Die Koeffizienten C_ij der Steifigkeitsmatrix haben die Dimension von Kraft pro Fläche und sind Parameter des Materials. Die Materialparameter können nicht beliebig gewählt werden, sondern müssen gewissen Stabilitätskriterien genügen. Diese folgen aus der Forderung, dass die Steifigkeits- und Nachgiebigkeitsmatrizen positiv definit sein müssen, was der Fall ist, wenn sämtliche ihrer sechs Eigenwerte positiv sind. Notwendig dafür ist:

Alle Diagonalelemente der Steifigkeits- und Nachgiebigkeitsmatrix müssen positiv sein (damit sich das Material in Zugrichtung streckt, wenn man daran zieht, und nicht staucht) und
die Determinante der Steifigkeits- und Nachgiebigkeitsmatrix muss positiv sein (damit es unter Druck komprimiert und nicht expandiert).

Werden an einem realen Werkstoff Materialparameter identifiziert, die diesen Stabilitätskriterien widersprechen, ist Vorsicht geboten. Die notwendigen und hinreichenden Stabilitätskriterien lauten, ausgedrückt mit den Koeffizienten S_ij der Nachgiebigkeitsmatrix:[4]^:644

S₁₂² < S₁₁S₂₂	S₁₃² < S₁₁S₃₃	S₂₃² < S₂₂S₃₃
S₁₆² < S₁₁S₆₆	S₂₆² < S₂₂S₆₆	S₃₆² < S₃₃S₆₆
S₄₅² < S₄₄S₅₅
S₁₁(S₂₂S₃₃-S₂₃²)-S₁₂(S₁₂S₃₃-S₁₃S₂₃)+S₁₃(S₁₂S₂₃-S₂₂S₁₃)>0
S₁₁(S₂₂S₆₆-S₂₆²)-S₁₂(S₁₂S₆₆-S₁₆S₂₆)+S₁₆(S₁₂S₂₆-S₁₆S₂₂)>0
S₁₁(S₃₃S₆₆-S₃₆²)-S₁₃(S₁₃S₆₆-S₁₆S₃₆)+S₁₆(S₁₃S₃₆-S₁₆S₃₃)>0
S₂₂(S₃₃S₆₆-S₃₆²)-S₂₃(S₂₃S₆₆-S₂₆S₃₆)+S₂₆(S₂₃S₃₆-S₂₆S₃₃)>0
S₁₆S₂₆(S₃₃S₁₂-S₁₃S₂₃)+S₂₆S₃₆(S₁₁S₂₃-S₁₂S₁₃)+S₁₆S₃₆(S₂₂S₁₃-S₁₂S₂₃) ...+½S₆₆(S₁₁S₂₂S₃₃+2S₁₂S₁₃S₂₃-S₁₁S₂₃²-S₂₂S₁₃²-S₃₃S₁₂²) ...+½S₁₆(S₂₃²-S₂₂S₃₃)+½S₂₆(S₁₃²-S₃₃S₁₁)+½S₃₆(S₁₂²-S₁₁S₂₂)>0

Hydrostatischer Spannungszustand und Kompressibilität

Der hydrostatische Spannungszustand stellt sich in einem allseitigem Druck ausgesetzten Körper ein. Wegen des auf der Erdoberfläche allgegenwärtigen Luftdrucks, ist dieser Zustand dort überall präsent. Wenn ein Körper aus kompressiblem isotropem Material zusammengedrückt wird, dann schrumpft er in allen Raumrichtungen gleichermaßen. Ein kompressibles monoklin anisotropes Material schrumpft in jeder Raumrichtung unterschiedlich und wird dabei geschert.

Das ist am einfachsten mit der Nachgiebigkeitsmatrix S nachzuweisen, die an denselben Stellen von null verschiedene Einträge S_ij aufweist wie die Steifigkeitsmatrix:

{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\2\varepsilon _{4}\\2\varepsilon _{5}\\2\varepsilon _{6}\\\end{bmatrix}}={\begin{bmatrix}S_{11}&S_{12}&S_{13}&0&0&S_{16}\\S_{12}&S_{22}&S_{23}&0&0&S_{26}\\S_{13}&S_{23}&S_{33}&0&0&S_{36}\\0&0&0&S_{44}&S_{45}&0\\0&0&0&S_{45}&S_{55}&0\\S_{16}&S_{26}&S_{36}&0&0&S_{66}\end{bmatrix}}{\begin{bmatrix}-p\\-p\\-p\\0\\0\\0\end{bmatrix}}=-p{\begin{bmatrix}S_{11}+S_{12}+S_{13}\\S_{12}+S_{22}+S_{23}\\S_{13}+S_{23}+S_{33}\\0\\0\\S_{16}+S_{26}+S_{36}\end{bmatrix}}

Darin ist p der Druck. Beim monoklin anisotropen linear elastischen Werkstoff kommt es bei allseitigem Druck zur Scherung

\gamma _{12}:=2\varepsilon _{6}=-p(S_{16}+S_{26}+S_{36})

dem letzten Eintrag im rechten Vektor, eine Eigenschaft die nur noch die Trikline Anisotropie aufweist.

Die Kompression wird von den oberen drei Einträgen im rechten Vektor repräsentiert und wenn die Summe gemäß

S_{11}+S_{22}+S_{33}+2(S_{23}+S_{13}+S_{12})=0

verschwindet, dann ist das Material in erster Näherung inkompressibel, siehe Deviator. Ist die Summe nicht null, dann ergibt sich der Kompressionsmodul K aus dem Kehrwert:

{\begin{aligned}&\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3}=\varepsilon _{v}={\frac {\mathrm {v} -V}{V}}=-p\cdot [S_{11}+S_{22}+S_{33}+2(S_{23}+S_{13}+S_{12})]\\&\rightarrow K:=-{\frac {\mathrm {d} p}{\frac {\mathrm {d} \mathrm {v} }{V}}}={\frac {1}{S_{11}+S_{22}+S_{33}+2(S_{23}+S_{13}+S_{12})}}\end{aligned}}

Darin ist V das Volumen bei p=0 und v dasjenige beim aktuellen Druck.

Herleitung

In der Hyperelastizität ergeben sich die Spannungen aus der Ableitung der Formänderungsenergie nach den Dehnungen. Damit die Spannungen linear in den Dehnungen sind, muss demnach die Formänderungsenergie quadratisch in den Dehnungen sein, denn nur dann ist ihre Ableitung linear. Unter Verwendung der #Invarianten ergibt sich der Ansatz

{\begin{aligned}w({\boldsymbol {\varepsilon }}):=&{\frac {a}{2}}\varepsilon _{11}^{2}+{\frac {b}{2}}\varepsilon _{22}^{2}+{\frac {c}{2}}\varepsilon _{33}^{2}+d\varepsilon _{11}\varepsilon _{22}+e\varepsilon _{11}\varepsilon _{33}+f\varepsilon _{22}\varepsilon _{33}\\&+2g\varepsilon _{11}\varepsilon _{12}+2h\varepsilon _{22}\varepsilon _{12}+2q\varepsilon _{33}\varepsilon _{12}+2r\varepsilon _{23}^{2}+2s\varepsilon _{13}^{2}+2t\varepsilon _{12}^{2}\\&+4u\varepsilon _{13}\varepsilon _{23}\end{aligned}}

mit 13 Parametern a bis u. Nicht-linear hyperelastisches Verhalten kann modelliert werden, indem die Parameter a bis u durch Funktionen der Invarianten ersetzt werden, siehe Hyperelastizität#Orthotrope Hyperelastizität.[1]^:380

Um die Formänderungsenergie nach ε ableiten zu können, müssen die Komponenten ε_ij als Funktion des Tensors ε ausgedrückt werden. Dies gelingt mit der Darstellung des Frobenius-Skalarprodukts ":" als Spur:

\mathbf {A

Darin bedeutet "·" das Matrizenprodukt und das hochgestellte ⊤ eine Transponierung. Mit der Abkürzung $\mathbf {K} _{ij}={\tfrac {1}{2}}({\hat {e}}_{i}\otimes {\hat {e}}_{j}+{\hat {e}}_{j}\otimes {\hat {e}}_{i})$ für die symmetrisierten dyadischen Produkte ⊗ der #Strukturvektoren ist dann[5]

\mathbf {K} _{ij}:{\boldsymbol {\varepsilon }}={\frac {1}{2}}(\varepsilon _{ij}+\varepsilon _{ji})=\varepsilon _{ij}\quad \rightarrow \quad {\frac {\mathrm {d} \varepsilon _{ij}}{\mathrm {d} {\boldsymbol {\varepsilon }}}}=\mathbf {K} _{ij}

Aus dem Ansatz der Formänderungsenergie berechnen sich die Spannungen zu

{\begin{aligned}{\boldsymbol {\sigma }}={\frac {\mathrm {d} w}{\mathrm {d} {\boldsymbol {\varepsilon }}}}=&a\varepsilon _{11}\mathbf {K} _{11}+b\varepsilon _{22}\mathbf {K} _{22}+c\varepsilon _{33}\mathbf {K} _{33}\\&+d(\varepsilon _{11}\mathbf {K} _{22}+\varepsilon _{22}\mathbf {K} _{11})+e(\varepsilon _{11}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{11})+f(\varepsilon _{22}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{22})\\&+2g(\varepsilon _{12}\mathbf {K} _{11}+\varepsilon _{11}\mathbf {K} _{12})+2h(\varepsilon _{12}\mathbf {K} _{22}+\varepsilon _{22}\mathbf {K} _{12})+2q(\varepsilon _{12}\mathbf {K} _{33}+\varepsilon _{33}\mathbf {K} _{12})\\&+4r\varepsilon _{23}\mathbf {K} _{23}+4s\varepsilon _{13}\mathbf {K} _{13}+4t\varepsilon _{12}\mathbf {K} _{12}\\&+4u(\varepsilon _{13}\mathbf {K} _{23}+\varepsilon _{23}\mathbf {K} _{13})\end{aligned}}

oder in Voigt-Notation im ê_1,2,3-System

{\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{23}\\\sigma _{13}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}a\varepsilon _{11}+d\varepsilon _{22}+e\varepsilon _{33}+2g\varepsilon _{12}\\b\varepsilon _{22}+d\varepsilon _{11}+f\varepsilon _{33}+2h\varepsilon _{12}\\e\varepsilon _{11}+f\varepsilon _{22}+c\varepsilon _{33}+2q\varepsilon _{12}\\2(r\varepsilon _{23}+u\varepsilon _{13})\\2(u\varepsilon _{23}+s\varepsilon _{13})\\g\varepsilon _{11}+h\varepsilon _{22}+q\varepsilon _{33}+2t\varepsilon _{12}\end{bmatrix}}={\begin{bmatrix}a&d&e&0&0&g\\d&b&f&0&0&h\\e&f&c&0&0&q\\0&0&0&r&u&0\\0&0&0&u&s&0\\g&h&q&0&0&t\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\2\varepsilon _{23}\\2\varepsilon _{13}\\2\varepsilon _{12}\end{bmatrix}}

Die Parameter lassen sich den Einträgen in der #Steifigkeitsmatrix direkt zuordnen. Ableitung der Spannungen nach den Dehnungen liefert den konstanten und symmetrischen Elastizitätstensor 4. Stufe:

{\begin{aligned}\mathbb {C

Die Voigt-Notation der Tensoren K_ij mit i≠j besitzen den Eintrag ½ an einer Stelle und sonst nur nullen. Mit den Definitionen V_i=K_ii für i=1,2,3 und V₄=2K₂₃, V₅=2K₁₃ sowie V₆=2K₁₂, deren Koeffizienten nur Nullen und Einsen sind, entsteht eine Darstellung des Elastizitätstensors, an der seine Voigt-Notation direkt ablesbar ist:

{\begin{aligned}\mathbb {C} =&(&a\mathbf {V} _{1}&+d\mathbf {V} _{2}&+e\mathbf {V} _{3}&&&+g\mathbf {V} _{6}&)\otimes \mathbf {V} _{1}\\&+(&d\mathbf {V} _{1}&+b\mathbf {V} _{2}&+f\mathbf {V} _{3}&&&+h\mathbf {V} _{6}&)\otimes \mathbf {V} _{2}\\&+(&e\mathbf {V} _{1}&+f\mathbf {V} _{2}&+c\mathbf {V} _{3}&&&+q\mathbf {V} _{6}&)\otimes \mathbf {V} _{3}\\&+(&&&&r\mathbf {V} _{4}&+u\mathbf {V} _{5}&&)\otimes \mathbf {V} _{4}\\&+(&&&&u\mathbf {V} _{4}&+s\mathbf {V} _{5}&&)\otimes \mathbf {V} _{5}\\&+(&g\mathbf {V} _{1}&+h\mathbf {V} _{2}&+q\mathbf {V} _{3}&&&+t\mathbf {V} _{6}&)\otimes \mathbf {V} _{6}\end{aligned}}

Gründe für die Besetztheit der Steifigkeitsmatrix

In diesem Abschnitt wird die Frage geklärt, warum die Steifigkeitsmatrix nur an den gegebenen Stellen besetzt ist. In der Steifigkeitsmatrix können 21 unabhängige Materialkonstanten auftreten; im Fall der monoklinen Anisotropie sind es 13. Warum das so ist, wird nachfolgend dargestellt.

Das maßgebliche Element der #Symmetriegruppe ist die 180-Grad-Drehung um die 3-Achse. Der entsprechende orthogonale Tensor kann im 123-System mit einer Drehmatrix

\mathbf {Q} ={\begin{pmatrix}-1\\&-1\\&&1\end{pmatrix}}

identifiziert werden. Dann ist bei monokliner Anisotropie

w({\boldsymbol {\varepsilon }})=w(\mathbf {Q} \cdot {\boldsymbol {\varepsilon }}\cdot \mathbf {Q} ^{\top })

Wegen

{\boldsymbol {\varepsilon }}':=\mathbf {Q} \cdot {\boldsymbol {\varepsilon }}\cdot \mathbf {Q} ^{\top }={\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{12}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _{13}&\varepsilon _{23}&\varepsilon _{33}\end{pmatrix}}{\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&1\end{pmatrix}}={\begin{pmatrix}\varepsilon _{11}&\varepsilon _{12}&-\varepsilon _{13}\\\varepsilon _{12}&\varepsilon _{22}&-\varepsilon _{23}\\-\varepsilon _{13}&-\varepsilon _{23}&\varepsilon _{33}\end{pmatrix}}

sind die Voigt-Notationen der Verzerrungstensoren

[{\boldsymbol {\varepsilon }}]={\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\2\varepsilon _{23}\\2\varepsilon _{13}\\2\varepsilon _{12}\end{bmatrix}},\quad [{\boldsymbol {\varepsilon }}']={\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\-2\varepsilon _{23}\\-2\varepsilon _{13}\\2\varepsilon _{12}\end{bmatrix}}

Obige Bedingung an die Formänderungsenergie lautet mit diesen Vektoren und der Steifigkeitsmatrix C

w({\boldsymbol {\varepsilon }})={\frac {1}{2}}[{\boldsymbol {\varepsilon }}]^{\top }C[{\boldsymbol {\varepsilon }}]=w({\boldsymbol {\varepsilon }}')={\frac {1}{2}}[{\boldsymbol {\varepsilon }}']^{\top }C[{\boldsymbol {\varepsilon }}']={\frac {1}{2}}[{\boldsymbol {\varepsilon }}]^{\top }C'[{\boldsymbol {\varepsilon }}]\quad \rightarrow \quad C'=C

wo die negativen Einträge in ε' auf die Steifigkeitsmatrix C' übertragen wurden:

C={\begin{bmatrix}C_{11}&C_{12}&C_{13}&C_{14}&C_{15}&C_{16}\\C_{12}&C_{22}&C_{23}&C_{24}&C_{25}&C_{26}\\C_{13}&C_{23}&C_{33}&C_{34}&C_{35}&C_{36}\\C_{14}&C_{24}&C_{34}&C_{44}&C_{45}&C_{46}\\C_{15}&C_{25}&C_{35}&C_{45}&C_{55}&C_{56}\\C_{16}&C_{26}&C_{36}&C_{46}&C_{56}&C_{66}\end{bmatrix}}

und

C'={\begin{bmatrix}C_{11}&C_{12}&C_{13}&-C_{14}&-C_{15}&C_{16}\\C_{12}&C_{22}&C_{23}&-C_{24}&-C_{25}&C_{26}\\C_{13}&C_{23}&C_{33}&-C_{34}&-C_{35}&C_{36}\\-C_{14}&-C_{24}&-C_{34}&C_{44}&C_{45}&-C_{46}\\-C_{15}&-C_{25}&-C_{35}&C_{45}&C_{55}&-C_{56}\\C_{16}&C_{26}&C_{36}&-C_{46}&-C_{56}&C_{66}\end{bmatrix}}

C=C' ist komponentenweise zu erfüllen und erzwingt $C_{14}=C_{15}=C_{24}=C_{25}=C_{34}=C_{35}=C_{46}=C_{56}=0$ mit der Konsequenz

C=C'={\begin{bmatrix}C_{11}&C_{12}&C_{13}&0&0&C_{16}\\C_{12}&C_{22}&C_{23}&0&0&C_{26}\\C_{13}&C_{23}&C_{33}&0&0&C_{36}\\0&0&0&C_{44}&C_{45}&0\\0&0&0&C_{45}&C_{55}&0\\C_{16}&C_{26}&C_{36}&0&0&C_{66}\end{bmatrix}}

was zu zeigen war.

Siehe auch

Einzelnachweise

P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 978-3-642-07718-0.
Monoclinic Material. ScienceDirect, abgerufen am 3. Oktober 2021 (englisch).
Xu-Shan Zhao, Shun-Li Shang, Zi-Kui Liu, Jian-Yun Shen: Elastic properties of cubic, tetragonal and monoclinic ZrO₂ from first-principles calculations. In: Journal of Nuclear Materials. Band 415, Nr. 1. Elsevier B.V., 1. August 2011, ISSN 0022-3115, S. 13–17, doi:10.1016/j.jnucmat.2011.05.016.
P. S. Theocaris, D. P. Sokolis: Spectral decomposition of the linear elastic tensor for monoclinic symmetry. In: Acta Cryst. Section A, Foundations of crystallography. Band 55, Nr. 4, 7. Dezember 1999, S. 635–647, doi:10.1107/S0108767398016766 (researchgate.net [abgerufen am 3. Oktober 2021]).
Die ij-Komponente eines beliebigen Tensors zweiter Stufe T im ê_1,2,3-System ist
${\begin{aligned}T_{ij}:=&{\hat {e}}_{i}\cdot \mathbf {T} \cdot {\hat {e}}_{j}={\hat {e}}_{j}\cdot ({\hat {e}}_{i}\cdot \mathbf {T} )\\=&\mathrm {Spur} ({\hat {e}}_{j}\otimes {\hat {e}}_{i}\cdot \mathbf {T} ):=({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {T} \end{aligned}}$
Die Fréchet-Ableitung hiervon nach T ist der beschränkte lineare Operator ${\mathcal {A}}$ der – sofern er existiert – in allen Richtungen H dem Gâteaux-Differential entspricht, also
${\begin{aligned}{\mathcal {A}}(\mathbf {H} )=&\left.{\frac {\mathrm {d} }{\mathrm {d} s}}[({\hat {e}}_{i}\otimes {\hat {e}}_{j}):(\mathbf {T} +s\mathbf {H} )]\right|_{s=0}\\=&({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} \quad \forall \;\mathbf {H} \end{aligned}}$
Darin ist $s\in \mathbb {R}$ und der lineare Operator ist das Skalarprodukt mit ${\hat {e}}_{i}\otimes {\hat {e}}_{j}$ . Hier ist $\mathbf {T} ={\boldsymbol {\varepsilon }}$ ein symmetrischer Tensor, dessen Differential H auch ein symmetrischer Tensor ist. Beim Skalarprodukt mit diesem trägt nur der symmetrische Anteil etwas bei:
$({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} ={\frac {1}{2}}({\hat {e}}_{i}\otimes {\hat {e}}_{j}+{\hat {e}}_{j}\otimes {\hat {e}}_{i}):\mathbf {H} =\mathbf {K} _{ij}:\mathbf {H}$
Dann wird auch
${\mathcal {A}}={\frac {\partial T_{ij}}{\partial \mathbf {T} }}=\mathbf {K} _{ij}$
geschrieben.

Literatur

J.F. Nye: Physical Properties of Crystals: Their Representation by Tensors and Matrices. Oxford University Press, 1985, ISBN 978-0-19-851165-6.
H. Altenbach, J. Altenbach, R. Rikards: Einführung in die Mechanik der Laminat- und Sandwichtragwerke. Deutscher Verlag für Grundstoffindustrie, Stuttgart 1996, ISBN 3-342-00681-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[haupt-1] P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 978-3-642-07718-0.

[2] Monoclinic Material. ScienceDirect, abgerufen am 3. Oktober 2021 (englisch).

[3] Xu-Shan Zhao, Shun-Li Shang, Zi-Kui Liu, Jian-Yun Shen: Elastic properties of cubic, tetragonal and monoclinic ZrO₂ from first-principles calculations. In: Journal of Nuclear Materials. Band 415, Nr. 1. Elsevier B.V., 1. August 2011, ISSN 0022-3115, S. 13–17, doi:10.1016/j.jnucmat.2011.05.016.

[sokolis-4] P. S. Theocaris, D. P. Sokolis: Spectral decomposition of the linear elastic tensor for monoclinic symmetry. In: Acta Cryst. Section A, Foundations of crystallography. Band 55, Nr. 4, 7. Dezember 1999, S. 635–647, doi:10.1107/S0108767398016766 (researchgate.net [abgerufen am 3. Oktober 2021]).

[Frechet-5] Die ij-Komponente eines beliebigen Tensors zweiter Stufe T im ê_1,2,3-System ist
${\begin{aligned}T_{ij}:=&{\hat {e}}_{i}\cdot \mathbf {T} \cdot {\hat {e}}_{j}={\hat {e}}_{j}\cdot ({\hat {e}}_{i}\cdot \mathbf {T} )\\=&\mathrm {Spur} ({\hat {e}}_{j}\otimes {\hat {e}}_{i}\cdot \mathbf {T} ):=({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {T} \end{aligned}}$
Die Fréchet-Ableitung hiervon nach T ist der beschränkte lineare Operator ${\mathcal {A}}$ der – sofern er existiert – in allen Richtungen H dem Gâteaux-Differential entspricht, also
${\begin{aligned}{\mathcal {A}}(\mathbf {H} )=&\left.{\frac {\mathrm {d} }{\mathrm {d} s}}[({\hat {e}}_{i}\otimes {\hat {e}}_{j}):(\mathbf {T} +s\mathbf {H} )]\right|_{s=0}\\=&({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} \quad \forall \;\mathbf {H} \end{aligned}}$
Darin ist $s\in \mathbb {R}$ und der lineare Operator ist das Skalarprodukt mit ${\hat {e}}_{i}\otimes {\hat {e}}_{j}$ . Hier ist $\mathbf {T} ={\boldsymbol {\varepsilon }}$ ein symmetrischer Tensor, dessen Differential H auch ein symmetrischer Tensor ist. Beim Skalarprodukt mit diesem trägt nur der symmetrische Anteil etwas bei:
$({\hat {e}}_{i}\otimes {\hat {e}}_{j}):\mathbf {H} ={\frac {1}{2}}({\hat {e}}_{i}\otimes {\hat {e}}_{j}+{\hat {e}}_{j}\otimes {\hat {e}}_{i}):\mathbf {H} =\mathbf {K} _{ij}:\mathbf {H}$
Dann wird auch
${\mathcal {A}}={\frac {\partial T_{ij}}{\partial \mathbf {T} }}=\mathbf {K} _{ij}$
geschrieben.