Hyperelastizität
Hyperelastizität oder Green’sche Elastizität (von griechisch ὑπέρ hyper „über“, ελαστικός elastikos „anpassungsfähig“ und George Green) ist ein Materialmodell der Elastizität. Elastizität ist die Eigenschaft eines Körpers, unter Krafteinwirkung seine Form zu verändern und bei Wegfall der einwirkenden Kraft in die Ursprungsform zurückzukehren (Beispiel: Sprungfeder). Als Ursache der Elastizität kommen Verzerrungen des Atomgitters (bei Metallen), das Dehnen von Molekülketten (Gummi und Kunststoffe) oder die Änderung des mittleren Atomabstandes (Flüssigkeiten und Gase) in Frage.
Für viele Materialien beschreibt die lineare Elastizität das beobachtete Materialverhalten nicht genau. Das bekannteste Beispiel mit nichtlinear elastischem Verhalten ist Gummi, das großen Verformungen standhält und dessen Reaktionen in guter Näherung mit Hyperelastizität nachgebildet werden können. Auch biologische Gewebe werden mit Hyperelastizität modelliert.[1] Alle barotropen reibungsfreien Flüssigkeiten und Gase sind gleichsam Cauchy-elastisch und hyperelastisch, worauf in der Cauchy-Elastizität eingegangen wird. Der vorliegende Artikel befasst sich mit Feststoffmodellen. Hier ist die Hyperelastizität derjenige Spezialfall der Cauchy-Elastizität, in dem das Materialverhalten konservativ ist.
Ronald Rivlin und Melvin Mooney entwickelten die ersten Feststoffmodelle der Hyperelastizität, das Neo-Hooke- bzw. das Mooney-Rivlin-Modell. Andere oft benutzte Materialmodelle sind das Ogden- und Arruda-Boyce-Modell.
Beschreibung
Makroskopisches Verhalten
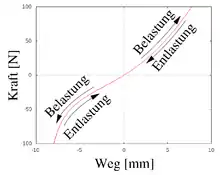
Makroskopisch lassen sich folgende Eigenschaften an einem hyperelastischen Körper beobachten:
- Bei gegebener Verformung haben die Reaktionskräfte unabhängig von der Vorgeschichte immer denselben Wert.
- Ist der Ausgangszustand unbelastet, so wird dieser nach jedweder Verformung wieder eingenommen, wenn die Belastungen entfernt werden.
- Das Materialverhalten ist geschwindigkeitsunabhängig. Die Geschwindigkeit, mit der eine Verformung stattfindet, hat keinen Einfluss auf den Widerstand, den der Körper der Verformung entgegensetzt.
- Im einachsigen Zugversuch erfolgen Be- und Entlastung stets entlang des gleichen Weges so wie im nebenstehenden Bild.
- Die aufgewendete Verformungsarbeit wird vollständig als Verzerrungsenergie im Körper gespeichert. Das Material ist somit konservativ.
Die ersten vier Eigenschaften charakterisieren die Cauchy-Elastizität. Wenn das Material zusätzlich noch die letzte Eigenschaft besitzt, dann ist das Material hyperelastisch.
Zeitunabhängigkeit
In der Hyperelastizität sind die Reaktionskräfte bei der Verformung eines Körpers ausschließlich von der aktuellen Verformung bestimmt. Ist der Ausgangszustand kräftefrei, so wird dieser nach jedweder Verformung wieder eingenommen, wenn die Belastungen entfernt werden. Verschiedene Verformungspfade, die am Ende dieselben Verformungen zur Folge haben, resultieren am Ende in denselben Reaktionskräften. Auch die Deformationsgeschwindigkeiten haben auf Materialgleichungsebene keinen Einfluss auf die Reaktionen. Die Vorgeschichte des Materials hat in dieser Idealisierung keinen Einfluss auf das aktuelle Materialverhalten. Hyperelastizität ist eine zeitunabhängige Materialeigenschaft.
Konservativität
Zusätzlich zur Cauchy-Elastizität ist in der Hyperelastizität die Formänderungsarbeit wegunabhängig, was sich darin ausdrückt, dass die Formänderungsarbeit nur vom Start- und Endpunkt des Verformungsweges, nicht aber von dessen Verlauf abhängt. Im Spezialfall der Übereinstimmung von Start- und Endpunkt ergibt sich: Entlang eines geschlossenen Verformungsweges wird keine Arbeit verrichtet oder Energie verbraucht. Aufgewandte Arbeiten werden vom Körper bis zur Rückkehr zum Ausgangspunkt vollständig zurückgegeben. Die Konservativität folgt hier auch daraus, dass die Verformungsleistung exakt die Rate der Formänderungsenergie ist, aufgewandte Arbeiten also vollständig (dissipationslos) in Formänderungsenergie umgesetzt werden. Verformungen sind hier reversibel.
Dissipative Vorgänge wie plastisches Fließen oder Kriechen sind damit ausgeschlossen, was bei realen Materialien innerhalb ihrer Elastizitätsgrenze der Fall ist. Reale Flüssigkeiten und Gase und manche Feststoffe (wie Eisen oder Glas) sind bei schnellen, geringfügigen Bewegungen (z. B. bei Schallwellen) in guter Näherung elastisch. Bei Feststoffen wird die Elastizitätsgrenze bei hinreichend kleinen und langsam vonstatten gehenden Verformungen eingehalten, die in vielen Anwendungen, insbesondere im technischen Bereich, vorliegen.
Lineare Hyperelastizität
Bei hinreichend kleinen Verformungen ist die Kraft-Weg-Beziehung bei Feststoffen linear und kann die Elastizität mit Moduln beschrieben werden. Weil die aufzuwendende Kraft und der zurückgelegte Weg bei einer Deformation maßgeblich von den Dimensionen des Körpers abhängen, wird die Kraft auf ihre Wirkfläche und der Weg auf eine geeignete Abmessung des Körpers bezogen. Die bezogene Kraft ist die Spannung und der bezogene Weg die Dehnung. Die Moduln quantifizieren das Verhältnis zwischen den Spannungen und den Dehnungen und sind eine Materialeigenschaft. Der Elastizitätsmodul gilt bei einachsigem Zug, der Schubmodul bei Scherung und der Kompressionsmodul bei allseitigem Zug/Druck. Bei einachsigem Zug tritt nicht nur in Zugrichtung eine Verformung auf, sondern auch quer dazu, was die dimensionslose Querdehnzahl quantifiziert. Die vollständige Beschreibung der isotropen linearen Hyperelastizität benötigt nur zwei der genannten Größen, kubische Anisotropie drei (ein Elastizitätsmodul, ein Schubmodul und eine Querdehnzahl), transversale Isotropie bereits fünf (zwei Elastizitätsmoduln, zwei Querdehnzahlen und einen Schubmodul) und die Orthotropie neun (drei Elastizitätsmoduln, drei Querdehnzahlen und drei Schubmoduln). Maximal werden jedoch 21 Parameter benötigt, um einen realen linear hyperelastischen Stoff zu beschreiben.
Definition
Zunächst wird das makroskopische Verhalten eines homogenen Zugstabes aus hyperelastischem Material zur Erläuterung herangezogen. Durch Übergang vom makroskopischen Körper zu einem Punkt im Kontinuum wird die Definition der Hyperelastizität nachgeholt.
Verhalten eines hyperelastischen Körpers

Wird ein homogener Stab aus hyperelastischem Material wie im Bild axial um einen Betrag gedehnt, dann wird dazu eine Kraft benötigt, die sich aus der Formänderungsenergie durch die Ableitung
berechnet. Im linearen Fall ist mit der Federkonstante D beispielsweise
Dreidimensionales Kontinuum
Die Übersetzung des Verhaltens des hyperelastischen Zugstabes in ein dreidimensionales Kontinuum erfolgt, indem
- die Kraft F durch einen Spannungstensor σ,
- die Verschiebung u durch einen Verzerrungstensor ε und
- die Formänderungsenergie W durch die spezifische Formänderungsenergie w
ausgetauscht wird. Dann berechnen sich die Spannungen σ aus der Ableitung[2] von w nach ε gemäß
Hier ist ρ die Dichte des Materials. Damit dieses Materialmodell das Prinzip der materiellen Objektivität erfüllt, muss die in der Cauchy-Elastizität beschriebene Modellierungsrichtlinie eingehalten werden, die besagt, dass als Spannungstensor der zweite Piola-Kirchhoff-Spannungstensor zu benutzen ist, der nur vom rechten Strecktensor U abhängen darf. Statt des rechten Strecktensors wird häufiger der Green-Lagrangesche Verzerrungstensor E = ½ (U · U – 1) mit dem Einheitstensor 1 oder der rechte-Cauchy-Green Tensor C = U · U benutzt:
Die Dichte ρ0 des Körpers ist in der hier eingesetzten lagrangeschen Darstellungsweise ein zeitlich konstanter Materialparameter.
Häufig[1] wird statt der spezifischen Formänderungsenergie die auf das Volumen bezogene Formänderungsenergie benutzt. Weil ρ0 ein konstanter Faktor ist, können die Formeln, die sich aus der auf die Masse oder das Volumen bezogenen Formänderungsenergie ergeben, jederzeit ineinander umgerechnet werden. Die Darstellung hier folgt Haupt[3].
In der Eulerschen Darstellungsweise ergibt sich daraus für den Cauchy’schen Spannungstensor:
Darin ist F der Deformationsgradient und
die Dichte im deformierten Körper, die von der Determinante det des Deformationsgradienten bemessen wird.
Bei isotropem Material kann gemäß
auch der linke-Cauchy-Green Tensor b = F · FT benutzt werden, der auch ein Strecktensor ist, siehe Hyperelastizität#Isotrope Hyperelastizität in räumlicher Darstellung unten.
Eigenschaften hyperelastischer Materialien
Dieser Abschnitt geht näher darauf ein, dass in der Hyperelastizität
- die Formänderungsarbeit nur vom Start- und Endpunkt des Verformungsweges, nicht aber von dessen Verlauf abhängt,
- entlang eines geschlossenen Verformungsweges keine Arbeit verrichtet oder Energie verbraucht wird, aufgewandte Arbeiten also vom Körper bis zur Rückkehr zum Ausgangspunkt vollständig zurückgegeben werden,
- die Verformungsleistung exakt die Rate der Formänderungsenergie ist, aufgewandte Arbeiten also vollständig (dissipationslos) als Formänderungsenergie gespeichert werden und
- Verformungen reversibel sind.
Verformungsarbeit
Im oben angegebenen Zugstab leistet die Kraft entlang eines Weges von bis die Arbeit
d. h., die verrichtete Arbeit ist nur vom Anfangs- und Endpunkt abhängig. Insbesondere verschwindet bei die verrichtete Arbeit:
Analog ist im Kontinuum die Spannungsarbeit das Kurvenintegral über einer mit der Zeit t parametrisierten Kurve
was die Wegunabhängigkeit und Konservativität (im Sonderfall ) nachweist. Das Rechenzeichen ":" bedeutet das Frobenius-Skalarprodukt und liefert hier die Summe der Arbeitsinkremente der Spannungskomponenten an den Komponenten des Deformationsgradienten.
Verformungsleistung
Die von der Kraft erbrachte Verformungsleistung im Stab lautet:
und ist die pro Zeiteinheit erbrachte Formänderungsarbeit. Die Leistung der Kraft wird also vollständig und dissipationslos in Formänderungsenergie umgesetzt. Im Kontinuum gilt in gleicher Weise
d. h., die spezifische Spannungsleistung ist bei Hyperelastizität die materielle Zeitableitung der spezifischen Formänderungsenergie.
Die Umkehrung gilt auch: Gibt es eine skalare Funktion , so dass die spezifische Spannungsleistung die materielle Zeitableitung dieser Funktion ist, dann ist das Material hyperelastisch.
In der eulerschen Formulierung entsteht
mit dem räumlichen Verzerrungsgeschwindigkeitstensor
der der symmetrische Anteil des Geschwindigkeitsgradienten ist.
Sätze über Hyperelastizität
Die folgenden Aussagen sind äquivalent:
- Das Material ist hyperelastisch.
- Die spezifische Spannungsleistung ist die materielle Zeitableitung der spezifischen Formänderungsenergie
- Die Arbeit der Spannungen entlang eines beliebigen Weges im Dehnungsraum ist nur vom Anfangs- und Endpunkt des Weges nicht aber von seinem Verlauf abhängig
- Die Arbeit der Spannungen entlang eines beliebigen geschlossenen Weges im Dehnungsraum verschwindet
- Die spezifische Spannungsarbeit an beliebigen differentiellen Dehnungsinkrementen ist gleich dem totalen Differential der spezifischen Formänderungsenergie
Bei der linearen Hyperelastizität sind die Spannungen als erste Ableitung der Formänderungsenergie linear in den Dehnungen und der Elastizitätstensor ist als zweite Ableitung konstant. Weil bei zwei Ableitungen hintereinander die Reihenfolge der Ableitungen vertauschbar ist, ist der Elastizitätstensor symmetrisch und kann ein linear-hyperelastischer Festkörper mit maximal 21 Parametern beschrieben werden.
Jedes barotrope elastische Fluid ist auch hyperelastisch.
Thermodynamische Konsistenz
Die Hyperelastizität ist im Einklang mit der Thermodynamik, wie eine Auswertung der Clausius-Duhem-Ungleichung zeigt, die den zweiten Hauptsatz der Thermodynamik in der Festkörpermechanik repräsentiert. Bei isothermer Zustandsänderung lautet die Clausius-Duhem-Ungleichung in der lagrangeschen Fassung
worin die helmholtzsche freie Energie darstellt. In der Hyperelastizität ist die Spannung die Ableitung[2] der Formänderungsenergie nach den Dehnungen und, weil die Formänderungsenergie nur eine Funktion der Dehnungen ist, folgt:
Identifikation der Formänderungsenergie mit der helmholtzschen freien Energie lässt die Hyperelastizität also im Einklang mit der Thermodynamik sein.
Inkompressibilität
Viele gummielastische Körper zeigen eine ausgeprägte Inkompressibilität und daher lohnt es sich diesen Fall näher zu betrachten. Inkompressibilität lässt sich mathematisch durch
ausdrücken, weshalb die Dichte dann zeitlich konstant ist:
Um die Inkompressibilität eines hyperelastischen Materials sicherzustellen, wird die spezifische Formänderungsenergie w0 erweitert:
Der Druck p ist eine zusätzliche, nicht-konstitutive Variable, die als Lagrange’scher Multiplikator zur Sicherstellung der Nebenbedingung J ≡ 1 eingeführt wird. Der Druck resultiert nun ausschließlich aus den Naturgesetzen und den Lagerungen des Körpers. Die Spannungen lauten hier
Isotrope Hyperelastizität
Wenn das Materialverhalten nicht richtungsabhängig ist, dann ist das Material isotrop. Nach einem Exkurs in lagrangescher Darstellung wird auf die Isotropie in der dort üblicheren eulerschen Betrachtungsweise eingegangen.
Isotrope Hyperelastizität in materieller Darstellung
In der isotropen Hyperelastizität ist die Formänderungsenergie in der lagrangeschen Darstellung eine Funktion der Hauptinvarianten I1,2,3 des rechten Cauchy-Green Strecktensors:
Diese Hauptinvarianten hängen über
mit dem Deformationsgradient zusammen. Der Operator bezeichnet die Spur. Der Kofaktor eines Tensors ist seine transponierte Adjunkte, die bei invertierbaren Tensoren, wie sie hier vorliegen,
lautet. Die Frobeniusnorm wird mit dem Frobenius-Skalarprodukt „:“ definiert:
Die Hauptinvarianten des rechten Cauchy-Green Tensors sind also Maße für die Änderung der Linien-, Flächen- und Volumenelemente.
Isotrope objektive Hyperelastizität impliziert also eine Spannungs-Deformations-Beziehung der Form
Die Umkehrung gilt auch: Wenn diese Spannungs-Deformations-Beziehung besteht, dann ist das Material objektiv, isotrop und hyperelastisch. Ein hyperelastisches Material ist also genau dann isotrop und objektiv, wenn sich die Formänderungsenergie als Funktion der Maße für die Änderung der Linien-, Flächen- und Volumenelemente schreiben lässt[4].
Die obige Formänderungsenergie ist polykonvex, wenn sie in jedem ihrer Argumente ║F║², ║cof(F)║² und det(F)² eine konvexe Funktion ist. Wenn diese Formänderungsenergie auch noch eine koerzitive Funktion jedes ihrer Argumente ist, dann existiert immer eine die Formänderungsenergie minimierende Deformation[5].
Isotrope Hyperelastizität in räumlicher Darstellung
Zumeist wird bei isotroper Hyperelastizität die Formänderungsenergie als isotrope Funktion des linken Cauchy-Green-Tensors b = F · FT angenommen. Dieser hat die Zeitableitung
Die unterstrichenen Terme sind für die Herleitung der letzten Identität eingefügte Einheitstensoren. Die Potenzialbeziehung zum Cauchy’schen Spannungstensor ergibt sich dann aus der Verformungsleistung
Hier wurde ausgenutzt, dass b und dw/db kommutieren, weil die Ableitung hier nach Voraussetzung eine isotrope Tensorfunktion des symmetrischen linken Cauchy-Green Tensors b ist.
Bei Inkompressibilität ist det(F) = √det(b) = 1 und daher
Die Formänderungsenergie hängt bei Isotropie nur von den Invarianten des symmetrischen und positiv definiten Tensors b oder des Linken Strecktensors v = +√b[6] ab, die also positive Eigenwerte haben. Die Formänderungsenergie wird üblicherweise mit den Eigenwerten λ1,2,3 von v oder den Hauptinvarianten
- I1(b) = Sp(b)
- I2(b) = ½(Sp(b)² - Sp(b)²)
- I3(b) = det(b)
ausgedrückt. Es liegen drei Formulierungen vor:
Der quergestrichene Strecktensor modelliert den volumenerhaltenden oder unimodularen Anteil der Verformung, denn seine Determinante ist konstant:
Seine Invarianten werden ebenfalls mit einem Quergestrich versehen:
Die folgenden Kapitel führen diese Varianten detailliert aus. Bei Inkompressibilität sind die ersten beiden Formulierungen äquivalent. Weil dann eine Abhängigkeit von der dritten Hauptinvariante oder J entfällt, wird der inkompressiblen isotropen Hyperelastizität ein eigener Abschnitt gewidmet. Der Aufwand für die Aufteilung in unimodularen und volumetrischen Anteil, den die zweite Formulierung charakterisiert, lohnt sich nur bei Kompressibilität. Die dritte Formulierung mit den Eigenwerten kann bei Kompressibilität und Inkompressibilität gleichermaßen angewendet werden.
Benutzung der Hauptinvarianten von b
Bei Kompressibilität hängt die Formänderungsenergie von allen drei Hauptinvarianten ab. Die folgende Tabelle gibt für symmetrische Tensoren gültige Ableitungen dieser Invarianten und der Formänderungsenergie.
| Ableitungen der Invarianten |
|---|
| Mit den für symmetrische Tensoren gültigen Ableitungen[2] berechnet sich die Ableitung der Formänderungsenergie: |
Als Resultat belaufen sich die Cauchy’schen Spannungen auf
Aufteilung in unimodularen und volumetrischen Anteil
Bei Kompressibilität können die Invarianten von
benutzt werden was den Vorteil hat, dass der volumetrische Kugelanteil und der unimodulare, gestaltändernde Anteil getrennt modelliert werden können. Es werden dann die Invarianten
eingesetzt. Die folgende Tabelle gibt für symmetrische Tensoren gültige Ableitungen dieser Invarianten und der Formänderungsenergie.
| Ableitungen der Hauptinvarianten bei Kompressibilität |
|---|
| Die Ableitungen[2] der Invarianten lauten: |
Als Resultat ergeben sich die Cauchy’schen Spannungen
Isotrope inkompressible Hyperelastizität
Bei Inkompressibilität entfällt eine Abhängigkeit von J weil J konstant gleich eins ist. Daher werden nur die Hauptinvarianten
eingesetzt. Die folgende Tabelle gibt für symmetrische Tensoren gültige Ableitungen dieser Invarianten und der Formänderungsenergie.
| Ableitungen der Hauptinvarianten bei Inkompressibilität |
|---|
| Die Ableitungen[2] der beiden Hauptinvarianten lauten für symmetrische Tensoren: |
Daraus resultiert die Darstellung
oder
wobei der Term dem unbestimmten Kugelanteil -p 1 zugeschlagen wurde.
Benutzung der Eigenwerte linken Strecktensors
Auch die Eigenwerte λ1,2,3 des linken Strecktensors v können als Invarianten benutzt werden und zwar sowohl bei Kompressibilität als auch bei Inkompressibilität. Die folgende Tabelle gibt für symmetrische Tensoren gültige Ableitungen der Eigenwerte und der Formänderungsenergie.
| Ableitungen der Eigenwerte von v |
|---|
| Die Eigenwerte von sind die Quadrate der Eigenwerte von aber beide Tensoren haben dieselben Eigenvektoren , die auf den Betrag eins normiert seien und deshalb mit Hut notiert werden. Die Eigenvektoren sind paarweise senkrecht aufeinander oder orthogonalisierbar weil und symmetrisch sind. Die Ableitung[2] der Eigenwerte ergibt sich zu |
Bei Verwendung der Eigenwerte ist also
Das Rechenzeichen „“ berechnet das dyadische Produkt und sind die auf eins normierten Eigenvektoren von . Im Fall der Inkompressibilität kann zusätzlich
eingesetzt werden.
Spezielle Formänderungsenergiefunktionen
Im Folgenden werden einige gebräuchliche Formänderungsenergiefunktionen vorgestellt.
Lineare Hyperelastizität
Die spezifische Formänderungsenergie, die auf das Hooke’sche Gesetz führt, lautet
Der Materialparameter ist der Schubmodul und die Querkontraktionszahl. Aus der zweiten Ableitung[2] nach den Verzerrungen berechnet sich der konstante und symmetrische Elastizitätstensor vierter Stufe
mit dem Einheitstensor vierter Stufe und der Lamé-Konstanten
Dieses Modell verallgemeinert das Hooke’sche Gesetz auf große Deformationen liefert aber nur bei moderaten Dehnungen physikalisch plausible Antworten. Die Dehnung, die dem Zusammendrücken eines Stabes auf null Länge entspricht, ergibt beispielsweise verschwindende Cauchy-Spannungen. Es approximiert aber jedwedes Modell der Hyperelastizität bei kleinen Dehnungen in erster Ordnung.
Mooney-Rivlin-Modell
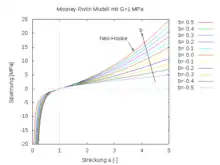
Eine Approximation zweiter Ordnung für inkompressible hyperelastische Körper stellt das Mooney-Rivlin-Modell
dar. Die Invarianten gehören zum Strecktensor , der Parameter ist der Schubmodul und die dimensionslose Kennziffer mit
repräsentiert Effekte zweiter Ordnung. Oftmals werden stattdessen die Parameter
benutzt, die beide nicht negativ sein dürfen.
Neo-Hooke-Modell
Das Neo-Hooke-Modell ist der Sonderfall
des Mooney-Rivlin Materials:
In dem ein volumetrischer Term hinzugefügt wird und die Invariante statt benutzt wird, entsteht eine auch bei großen Dehnungen plausible Verallgemeinerung des Hooke’schen Stoffgesetzes für kompressible Elastomere:
Der Parameter kontrolliert die Kompressibilität. Es wurden aber auch noch andere Formulierungen für den volumetrischen Anteil vorgeschlagen[7].
Ogden-Modell
Das Ogden-Modell ist ein Modell für inkompressible Hyperelastizität. Dieses Modell ist in den Eigenwerten des linken Strecktensors formuliert:
Die Zahlen μi und αi stellen die 2n Materialparameter dieses Modells dar und die Potenz eines Tensors wird wie ein Funktionswert berechnet[6].
Der Spezialfall n = 1 sowie α1 = 2 ergibt das Neo-Hooke-Modell und n = 2, α1 = 2 sowie α2 = −2 bilden das Mooney-Rivlin-Modell.
Näherung mit Taylorpolynomen
Wenn w(I1, I2) an der Stelle I1 = 3 und I2 = 3, was in der undeformierten Lage bei F = 1 der Fall ist, durch ein Taylorpolynom angenähert wird, entsteht:
Die Zahlen Cij sind Materialparameter. Auch in diesem Modell sind das Neo-Hooke- und Mooney-Rivlin-Modell als Spezialfälle enthalten.
Anisotrope Hyperelastizität
Bei einem transversal isotropen Material, wie z. B. unidirektional verstärktem Kunststoff, kann eine Probe beliebig um die Faserrichtung gedreht werden, senkrecht zur Faser aber nur um 180°, ohne dass sich die Formänderungsenergie bei gegebener Dehnung ändert. Diese Drehungen können in einer Menge zusammengefasst werden. Wenn zwei Drehungen aus hintereinander ausgeführt werden, wird wieder eine Drehung aus erhalten. Mit der 0°-Drehung als neutralem und der Rückdrehung als inversem Element stellt eine Gruppe dar: die Symmetriegruppe des Materials.
Allgemein wird die Richtungsabhängigkeit eines Materials durch die Symmetriegruppe des Materials beschrieben. Diese Gruppe beinhaltet alle Drehungen, die im materiellen Punkt stattfinden dürfen, ohne dass sich bei gegebener Dehnung die Formänderungsenergie ändert. Drehungen werden mathematisch mit orthogonalen Tensoren (mit ) beschrieben. Entsprechend ist die Symmetriegruppe des Materials die Menge von orthogonalen Tensoren die definiert ist über:
Eine spezifische Formänderungsenergie mit dieser Eigenschaft kann mit tensoriellen Strukturvariablen formuliert werden:
Allerdings ist es im Allgemeinen nicht einfach diese Strukturvariablen aufzufinden, die Tensoren zweiter, vierter oder sechster Stufe sein können.
Bei der transversalen Isotropie ist es jedoch einfach, denn es genügt eine Strukturvariable.
Transversal isotrope Hyperelastizität
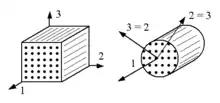
Der Werkstoff ist rotationssymmetrisch bezüglich der 1-Achse, die senkrecht auf der isotropen 2-3-Ebene steht.
Ein so orientierter Rundstab aus diesem Material kann um seine Längsachse gedreht werden, ohne dass sich seine Eigenschaften ändern.
Bei der transversal isotropen Hyperelastizität hat das Material eine Vorzugsrichtung, die 1-Richtung im Bild, in der das Material andere Eigenschaften hat als senkrecht dazu. In der 2-3-Ebene senkrecht zur Vorzugsrichtung verhält sich das Material isotrop. Die Vorzugsrichtung wird mit einem materiellen Linienelement der Länge eins definiert. Die dazu gehörende Strukturvariable ist der symmetrische Tensor
Die spezifische Formänderungsenergie hängt dann von den fünf Invarianten
ab, worin adj(E) die Adjunkte von E ist. Der zweite Piola-Kirchhoff-Tensor kann dann über die Ableitung[2]
berechnet werden. Das Materialgesetz der linear elastischen, transversalen Isotropie ist im Hauptartikel nachzuschlagen.
Orthotrope Hyperelastizität
Bei der orthtropen Hyperelastizität hat das Material keine Zug-Scher-Kopplung aber drei Vorzugsrichtungen, die paarweise senkrechten Orthotropieachsen, in der das Material andere Eigenschaften hat als senkrecht dazu. Die Symmetriegruppe dieses Materials beinhaltet alle 180° Drehungen um eine dieser drei Achsen. Die Strukturvariablen werden mit dem dyadischen Produkt von zwei materiellen Linienelementen der Länge eins definiert:
wobei hier vorausgesetzt wird. Die spezifische Formänderungsenergie hängt dann, neben den aus der transversalen Isotropie bekannten fünf Invarianten, noch von den Invarianten
und zwei weiteren Invarianten ab[8], die jedoch wegen keinen Beitrag liefern und hier nicht berücksichtigt zu werden brauchen. Der zweite Piola-Kirchhoff-Tensor kann nun über die Ableitung[2]
berechnet werden. Darin ist adj(E) die Adjunkte von E. Das Materialgesetz der linear elastischen Orthotropie ist im Hauptartikel nachzuschlagen.
Beispiel
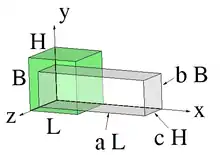
Ein homogener Klotz aus inkompressiblem hyperelastischem Material wird wie im Bild homogen mit den Faktoren in x-, y- bzw. z-Richtung gestreckt. Bei verbleibt der Klotz im Ausgangszustand. Dann ergeben sich der Deformationsgradient, der linke Cauchy-Green-Tensor und der linke Strecktensor
sowie die Invarianten und Eigenvektoren:
Wegen der angenommenen Inkompressibilität ist Für die Bedatung der Materialmodelle werden drei Versuche mit den Streckungen in der Tabelle durchgeführt, siehe auch die Bilder unten.
| Versuch | a | b | c |
|---|---|---|---|
| Uniaxialer Zug | |||
| Planarer Zug | |||
| Biaxialer Zug |
Das Mooney-Rivlin-Modell liefert dann mit
die Spannungen
Der Druck p errechnet sich aus den bei den Versuchen vorliegenden Randbedingungen.
Uniaxialer Zugversuch
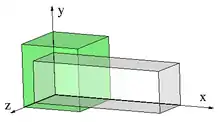
Hier hat man
und aus der Randbedingung σyy = σzz = 0 ermittelt man
und erhält so
Planarer Zugversuch

Hier hat man
und aus der Randbedingung σzz = 0 ermittelt man
und erhält so
Biaxialer Zugversuch
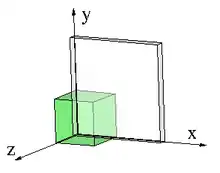
Hier hat man
und aus der Randbedingung σzz = 0 ermittelt man
und erhält so
Siehe auch
Einzelnachweise und Fußnoten
- Z. B. in Holzapfel (2000).
- Die Fréchet-Ableitung einer Funktion nach
ist der beschränkte lineare Operator der – sofern er existiert – in alle Richtungen dem Gâteaux-Differential entspricht, also
- Haupt (2000), S. 326ff
- P. G. Ciarlet (1988), Theorem 4.4-1
- John M. Ball: Convexity conditions and existence theorems in non-linear elasticity, Archive for Rational Mechanics and Analysis 63 (1977), S. 337–403
- Der Funktionswert f(T) eines Tensors T wird mit seiner Hauptachsentransformation, Bildung der Funktionswert der Diagonalelemente und Rücktransformation berechnet.
- Parisch (2003), S. 164
- Holzapfel (2000), S274
Literatur
- Horst Parisch: Festkörper Kontinuumsmechanik. Von den Grundgleichungen zur Lösung mit finiten Elementen. Teubner, Stuttgart 2003, ISBN 3-519-00434-8.
- Gerhard A. Holzapfel: Nonlinear Solid Mechanics. A Continuum Approach for Engineering. Wiley, Chichester 2010, ISBN 978-0-471-82319-3.(EA Chichester 2000)
- Philippe Ciarlet: Mathematical Elasticity, Bd. 1: Three-Dimensional Elasticity. North-Holland, Amsterdam 1988, ISBN 0-444-70259-8.(Studies in mathematics and its applications; Bd. 20)
- Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, Berlin 2000, ISBN 3-540-43111-X.