Gleichgewicht (Systemtheorie)

Im allgemeinen Sinn ist ein System im Gleichgewicht, wenn es sich ohne Einwirkung von außen zeitlich nicht verändert. Bei dynamischen Gleichgewichten werden im Allgemeinen nur makroskopische Veränderungen betrachtet.[1] Bei einem thermodynamischen Gleichgewicht ist beispielsweise der Makrozustand eines Gases mit den Zustandsgrößen Druck, Temperatur und chemisches Potential konstant, während sich der Mikrozustand, also die Position und Geschwindigkeit einzelner Gasteilchen ändern kann.

Der Zustand, den das System ohne Einwirkung von außen nicht verlässt, wird allgemein Gleichgewichtszustand, kritischer Punkt, Fixpunkt, stationärer Zustand, Gleichgewichtslage genannt. Je nach Kontext, werden die genannten Begriffe nicht synonym verwendet, sondern beinhalten eine zusätzliche Klassifizierung des Zustands, etwa hinsichtlich der Stabilität. Bei der Betrachtung von offenen Systemen, wird ein sich nicht ändernder Zustand als „stationärer Zustand“ bezeichnet, während der Begriff „Gleichgewicht“ für einen stationären Zustand nach Isolierung des Systems gebraucht wird.[2]

Allgemeine Definition

Betrachtet wird zunächst ein abgeschlossenes dynamisches System. Der Zustand eines dynamischen Systems zum Zeitpunkt $t$ , lässt sich allgemein durch ein Tupel $x\in \mathbb {R} ^{n}$ beschreiben, also eine geordnete Menge aller Zustandsgrößen. Damit der Zustand ein Gleichgewichtszustand ist, muss dieser für alle Zeiten gleich sein, man sagt auch „invariant gegenüber einer Dynamik $f$ “.

Die Lage und Anzahl der Gleichgewichtszustände eines Systems ist unabhängig davon, in welchem Zustand das System sich befindet, also auch unabhängig davon, ob es „im Gleichgewicht“ ist oder nicht. Die Gleichgewichtszustände ergeben sich als Lösungen der Gleichgewichtsbedingungen. Je nach Anzahl an Lösungen der Gleichungen für die jeweilige Gleichgewichtsbedingung, kann ein System beliebig viele Gleichgewichtszustände besitzen.

Kontinuierliches dynamisches System

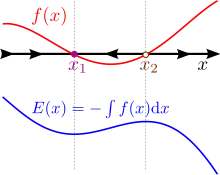
Beispiel für ein eindimensionales System. Die x-Achse ist der Zustandsraum; die schwarzen Pfeile zeigen die Zeitentwicklung. Die zwei Nullstellen der Funktion f sind die Gleichgewichtszustände x₁ und x₂. Die Funktion f lässt sich als negativer Gradient eines Potentials E darstellen.

Für ein kontinuierliches dynamisches System, dessen Zeitentwicklung gegeben ist durch die Differentialgleichung

{\frac {\mathrm {d} }{\mathrm {d} t}}x=f(x)

ist ein Gleichgewichtszustand $x(t)=x^{*}$ gegeben durch die Gleichgewichtsbedingung[3]

f(x^{*})=0

da dann entsprechend die zeitliche Ableitung $\textstyle {\frac {\mathrm {d} }{\mathrm {d} t}}x^{*}=0$ ist. Ein Gleichgewichtszustand ist also eine zeitunabhängige Lösung der gewöhnlichen Differentialgleichung bzw. eine Nullstelle der Funktion $f$ .

Diskretes dynamisches System

Konvergenz zu einem stationären Zustand in einem zeitdiskreten makroökonomischen Stock-Flow Consistent Model.

Ein diskretes dynamisches System, welches nur diskrete Zeitschritte erlaubt, lässt sich durch eine iterierte Abbildung

x_{n+1}=f(x_{n}),\qquad n=0,1,2\ldots

beschreiben. Die Gleichgewichtsbedingung für den Gleichgewichtszustand $x_{n}^{*}$ ist

x_{n}^{*}=f(x_{n}^{*}).

Der Gleichgewichtspunkt $x_{n}^{*}$ ist also ein zeitunabhängiger Fixpunkt der Abbildung $f$ .

Gleichgewichtszustand und Potential

Anstelle der Nullstellen der Funktion $f$ zu betrachten, lässt sich für viele Systeme ein Potential $E$ finden, sodass $f=-\nabla E$ sich als negativer Gradient des Potentials schreiben lässt. Ein Gleichgewichtszustand entspricht dann einem Extrempunkt des Potentials. Bei einem thermodynamischen System ist dies ein geeignetes thermodynamisches Potential. Zum Beispiel eignet sich für ein System bei konstanter Temperatur und Druck, wie eine chemische Reaktion, die Gibbs freie Enthalpie, welche minimal ist, wenn das System im thermodynamischen Gleichgewicht ist.

Bei einem Hamiltonschen System lässt sich der Zustand $x$ durch die Ortskoordinaten $q_{i}$ und Impulse $p_{i}$ beschreiben. Für ein Gleichgewichtszustand gilt $\textstyle {\frac {\mathrm {d} }{\mathrm {d} t}}q_{i}=0$ und $\textstyle {\frac {\mathrm {d} }{\mathrm {d} t}}p_{i}=0$ . Die Dynamik ist durch die kanonischen Gleichungen gegeben. Einsetzen der Gleichgewichtsbedingung ergibt, dass bei einem Gleichgewichtszustand die partiellen Ableitung der Hamiltonfunktion $\textstyle {\frac {\mathrm {d} H}{\mathrm {d} p_{i}}}$ und $\textstyle {\frac {\mathrm {d} H}{\mathrm {d} q_{i}}}$ Null sind, der Gleichgewichtszustand ist daher ein Extrempunkt des Potentials.

In der Mechanik wird der Ort mit den Koordinaten $q_{i}$ des Gleichgewichtszustandes auch Ruhelage oder statische Ruhelage genannt. Insbesondere erfährt ein Teilchen in der Ruhelage keinerlei Kraft. „Ruhelage“ ist in dieser Hinsicht etwas irreführend: Zwar wirkt auf ein Teilchen in der Ruhelage keine Kraft, das Teilchen muss sich dort allerdings keinesfalls in Ruhe befinden. Erst bei einem statischen Zustand, bei dem die Gleichgewichtsbedingung auch für die Impulse erfüllt ist, ist das Teilchen dort in Ruhe und das System im Gleichgewicht.

Verhalten von Gleichgewichten bei Störungen

Die zeitliche Entwicklung eines dynamischen Systems lässt sich qualitativ durch Charakterisieren der Gleichgewichtszustände abschätzen. Ein Gleichgewichtszustand lässt sich grob einteilen in

stabil: Das System kehrt nach einer Störung wieder in seinen Ausgangszustand zurück.
labil: Das System geht bei der kleinsten Störung in einen anderen Zustand über. Siehe aber auch Spontane Symmetriebrechung: Kuppel-Paradox
indifferent: Das System kommt nach jeder Störung in einem neuen Zustand zur Ruhe.
metastabil: Das System geht nach einer ausreichend großen Störung in einen stabileren Gleichgewichtszustand über. Bei zwei Gleichgewichtszuständen spricht man auch von bistabil.

stabiles Gleichgewicht
labiles Gleichgewicht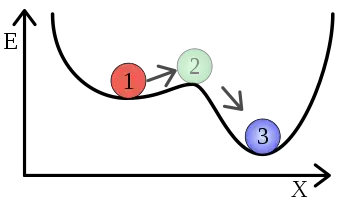
metastabiles Gleichgewicht
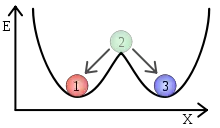bistabiles Gleichgewicht
indifferentes Gleichgewicht

Zur mathematisch exakten Einteilung gibt es in der Stabilitätstheorie mehrere Stabilitätsbegriffe. Im Folgenden wird ein kontinuierliches System angenommen, ähnliche Begriffe lassen sich auch für Systeme mit diskreten Zeitschritten definieren.

Ljapunov-stabil: Ein Gleichgewichtszustand $x^{*}$ ist Ljapunov-stabil, wenn eine hinreichend kleine Störung stets klein bleibt oder präziser: Für jedes $\varepsilon >0$ existiert ein $\delta >0$ derart, dass für alle Zeiten $t\geq 0$ und alle Trajektorien $x(t)$ mit $\|x(0)-x^{*}\|<\delta$ gilt: $\|x(t)-x^{*}\|<\varepsilon$ .
asymptotisch stabil: Ein Gleichgewichtszustand $x^{*}$ ist asymptotisch stabil, wenn er Ljapunov-stabil und attraktiv ist, also bei einer Störung wieder in den Gleichgewichtszustand zurückkehrt. Attraktiv bedeutet, dass es ein $\eta >0$ gibt, sodass jede Trajektorie $x(t)$ mit $\|x(0)-x^{*}\|<\eta$ für alle $t\geq 0$ existiert und die Bedingung $\lim _{t\to \infty }x(t)=x^{*}$ erfüllt.

Eine Methode zur Stabilitätsanalyse ist, das System um den Gleichgewichtszustand zu linearisieren. Mit dem Satz von Hartman-Grobman lässt sich der Gleichgewichtszustand dann anhand der Eigenwerte der Jacobi-Matrix charakterisieren.

Beispiele

Thermisches Gleichgewicht bei einem Haus

Der zeitliche Verlauf der Temperatur $T$ in einem ungeheizten Haus in Abhängigkeit von der Außentemperatur $T_{\mathrm {A} }$ lässt sich in einem einfachen Modell durch die Differentialgleichung

{\frac {\mathrm {d} }{\mathrm {d} t}}T=-k(T-T_{\mathrm {A} })

beschreiben. Die Konstante $k=A\alpha /C$ berechnet sich aus Fläche $A$ , Wärmeübergangskoeffizient $\alpha$ der Hauswände sowie der Wärmekapazität $C$ der Luft. Die Funktion $f(T)=-k(T-T_{\mathrm {A} })$ auf der rechten Seite der Gleichung bestimmt die Dynamik des Systems. Für einen Gleichgewichtszustand $T^{*}$ gilt

f(T^{*})=-k(T^{*}-T_{\mathrm {A} })=0

.

Das System besitzt also einen Gleichgewichtszustand bei $T^{*}=T_{\mathrm {A} }$ . Da die Ableitung

{\frac {\mathrm {d} f}{\mathrm {d} T}}(T^{*})=-k

negativ ist, ist der Gleichgewichtszustand $T^{*}$ stabil. Wenn das Haus wärmer bzw. kälter als die Umgebung ist, kühlt bzw. wärmt es sich solange auf, bis es diesen Gleichgewichtszustand erreicht. Auf diese Weise lassen sich durch die Bestimmung der Gleichgewichtspunkte und deren Stabilität Aussagen über das Verhalten des Systems treffen, ohne explizit den zeitlichen Verlauf $T(t)$ der Temperatur berechnen zu müssen. Die Integration der Gleichung, die für diese explizite Berechnung notwendig wäre, ist bei nichtlinearen Systemen im Allgemeinen nicht einfach oder analytisch nicht möglich.

Mechanisches Gleichgewicht bei einem ebenen Pendel

Ein ebenes Pendel als Fahrgeschäft auf einer Kirmes

Gleichgewichtspositionen des ebenen Pendels.

Phasenraum des ebenen Pendels mit Konstanten = 1. Das Potential und der Phasenraum sind bezüglich des Winkels θ periodisch mit Periode 2π.

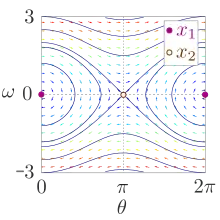
Ein ebenes Pendel ist ein mechanisches System, bei dem eine Masse mit einer Pendelstange fester Länge $l$ drehbar in einem Punkt befestigt ist. Der Zustand $\textstyle x=(\theta ,\omega )$ eines solchen Pendels zu einem festen Zeitpunkt $t$ lässt sich durch einen Winkel $\textstyle \theta \in [0,2\pi )$ und der Winkelgeschwindigkeit $\textstyle \omega \in \mathbb {R}$ beschreiben. Die Bewegungsgleichung ist dann die autonome Differentialgleichung

{\frac {\mathrm {d} }{\mathrm {d} t}}{\begin{pmatrix}\theta \\\omega \end{pmatrix}}={\begin{pmatrix}\omega \\{\frac {g}{l}}\sin \theta \end{pmatrix}}

wobei die Konstante $g$ die Fallbeschleunigung ist.

Das System hat damit zwei Gleichgewichtspunkte $x_{1}=(0,0)$ und $x_{2}=(\pi ,0)$ , welche die Gleichgewichtsbedingung erfüllen. Der Gleichgewichtspunkt $x_{1}$ bei einem Winkel von Null ist das stabile Gleichgewicht, wenn das Pendel keine Auslenkung und Geschwindigkeit besitzt. Der zweite Punkt $x_{2}$ ist das instabile Gleichgewicht, wenn das Pendel keine Geschwindigkeit besitzt und „auf dem Kopf“ steht. Im Phasenraum ist $x_{1}$ ein elliptischer Fixpunkt, der Punkt $x_{2}$ ein hyperbolischer Fixpunkt.

In einem statischen System, also ein System bei dem das Pendel keine Geschwindigkeit besitzt, lässt sich die Bedingung für ein mechanisches Gleichgewicht mithilfe von Kräften und Momenten formulieren. So ist das Pendel im Gleichgewicht, wenn die Summe aller angreifenden Kräfte und Momente Null ist. In beiden Gleichgewichtspunkten $x_{1}$ und $x_{2}$ wird die Gewichtskraft der Masse am Pendel durch die Kraft, mit der die Pendelstange die Masse am Drehpunkt festhält, vollständig ausgeglichen. Die resultierende Kraft und das resultierende Moment sind Null.

Ökologisches Gleichgewicht bei einer Räuber-Beute Beziehung

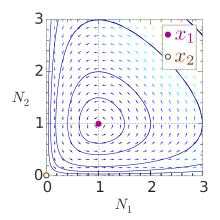
Phasenraum des Lotka-Volterra-Systems mit Konstanten = 1

Ein einfaches Modell der Wechselwirkung zwischen Räuber- und Beutepopulationen sind die Lotka-Volterra-Gleichungen. Sie beschreiben die zeitliche Entwicklung einer Anzahl an Beutetieren $N_{1}$ und Räubern $N_{2}$ . Mit den jeweiligen Reproduktions- und Sterberaten $\epsilon _{1}$ bzw. $\gamma _{2}$ und $\gamma _{1}$ bzw. $\epsilon _{2}$ ergibt sich das Differentialgleichungssystem für einen Zustand $x=(N_{1},N_{2})$ :

{\frac {\mathrm {d} }{\mathrm {d} t}}{\begin{pmatrix}N_{1}\\N_{2}\end{pmatrix}}={\begin{pmatrix}N_{1}\left(\epsilon _{1}-\gamma _{1}N_{2}\right)\\-N_{2}\left(\epsilon _{2}-\gamma _{2}N_{1}\right)\end{pmatrix}}

Das System besitzt einen stabilen Gleichgewichtspunkt $x_{1}=(\epsilon _{2}/\gamma _{2},\epsilon _{1}/\gamma _{1})$ und einen instabilen Gleichgewichtspunkt $x_{2}=(0,0)$ . Im Zustand $x_{1}$ gibt es eine konstante Anzahl an Räubern und Beutetieren, die in einem ökologischen Gleichgewicht sind. Im Zustand $x_{2}$ sind beide Populationen ausgerottet.

Dynamische Gleichgewichte

Ein System in der Natur lässt sich im Allgemeinen unterschiedlich beschreiben. So gibt es unterschiedlich detaillierte Möglichkeiten die Zustandsgrößen des Systems zu wählen. In der Statistischen Physik gibt es zur Unterscheidung unterschiedlich detaillierter Beschreibungen die Bezeichnungen Makrozustand und Mikrozustand. Bei Gleichgewichtsbetrachtungen, etwa bei einem thermodynamischen Gleichgewicht, wird nur der Makrozustand betrachtet. Das System ist im Gleichgewicht, wenn sich der Makrozustand nicht ändert. Der Mikrozustand des Systems kann sich jedoch ändern.

Gibt es Prozesse innerhalb des Systems oder Flüsse über die Systemgrenzen hinweg, die den Mikrozustand ändern, sich in ihrem Einfluss auf den Makrozustand des Systems gegenseitig aufheben, wird ein Gleichgewicht als dynamisches Gleichgewicht oder Fließgleichgewicht bezeichnet.

Dynamisches Gleichgewicht in einem geschlossenen System

Im Fall nicht-offener Systeme sind es nur innere Prozesse, die Einfluss auf die Zustandsgrößen des Systems haben. Die oben formulierte Gleichgewichtsbedingung ist in Systemen chemischer Reaktionen genau dann erfüllt, wenn die chemischen Potentiale ausgeglichen sind. Beispiel: Ein thermisch isolierter Drucktopf mit heißem Wasser und Wasserdampf. Die beiden beteiligten Reaktionen heißen Verdampfung und Kondensation. Verdampfung senkt die Temperatur und steigert den Druck, was weitere Verdampfung verlangsamt bzw. die Kondensation beschleunigt. Nach einiger Zeit stellt sich ein Gleichgewicht ein, in dem beide Reaktionen gleich schnell verlaufen und die Zustandsgrößen Druck, Temperatur und Dampfmenge konstant bleiben.

Für Systeme in dynamischem Gleichgewicht gilt der Virialsatz im jeweiligen Teilgebiet der Physik. Die explizite Kenntnis von Bahnen ist dafür nicht erforderlich.

Quasistatische Zustandsänderungen

Im Allgemeinen gibt es mehr als zwei Reaktionen, die gleichzeitig ablaufen. Das Gleichgewicht kann dann zwischen allen beteiligten Elementen des Systems bestehen oder sich auf ein Teilsystem beschränken. Sind die Prozesse des Teilsystems schnell gegenüber Austauschprozessen mit der Umgebung, so treten quasistatische Zustandsänderungen auf. Beispiel: Der langsam abkühlende Drucktopf. Die Abgabe von Wärme an die Umgebung senkt die Temperatur, den Druck und die Dampfmenge, aber nicht unabhängig voneinander, sondern der Systemzustand bleibt stets nahe an der Dampfdruckkurve.

Ob es in einem speziellen Fall eine Trennung in schnelle und langsame Prozesse gibt und wie die Änderungen der Zustandsgrößen zeitlich verlaufen, ist Gegenstand der Kinetik.

Fließgleichgewichte in offenen Systemen

Existieren mehrere Kopplungsprozesse mit der Umgebung, so kann der Zustand des Systems konstant bleiben, indem sich diese mehr oder weniger zufällig in ihrer Wirkung aufheben. Fließgleichgewichte sind stets mit einer Produktion von Entropie verbunden, die für einen stationären Zustand abgeführt werden muss.[4]

Enge Kopplung

Dominiert ein Kopplungsprozess die anderen Prozesse, so ist der Zustand des Teilsystems in der betroffenen Zustandsgröße festgelegt. Beispiele: Der Topf ist offen, der Druck ist auf den atmosphärischen Druck festgelegt, selbst große Heizleistung erhöht die Temperatur nicht über den Siedepunkt, solange noch Wasser im Topf ist. In der Elektrotechnik ist bei Anschluss eines Kleinverbrauchers an eine Spannungsquelle die Spannung festgelegt (geklemmt). Ein ökonomisches Beispiel ist die Buchpreisbindung (für Werke ohne Alternative, etwa spezielle Fachbücher).

Fließgleichgewicht im rückwirkungsfreien System

Ohne enge Kopplung werden Systeme meist mit deutlichen Änderungen ihres Zustandes auf Änderungen in der Umgebung reagieren. Die Bezeichnung Fließgleichgewicht legt folgendes Beispiel nahe: Der Füllstand einer Badewanne ohne Stöpsel wird sich bei gegebenem Zufluss so einpegeln, dass der vom Pegel abhängige Abfluss dem Zufluss gleich ist. Fließgleichgewichte gibt es aber auch mit vielen anderen physikalischen und nicht-physikalischen Größen, etwa Energie oder Reichtum.

Homöostatisches Gleichgewicht

Die Flüsse über die Systemgrenze können auch dadurch ausgeglichen werden, indem das System durch interne Regelungsprozesse auf sie Einfluss nimmt. Das Teilsystem eines komplexen Systems, das den Regelungsmechanismus bildet, nennt die Systemtheorie allgemein Homöostat, das prototypische Beispiel ist der Thermostat.

Der Begriff Homöostase wurde im Zusammenhang mit lebenden Systemen geprägt, in denen meist viele Systemparameter einer Regelung unterliegen: pH-Wert, osmotischer Druck, Enzymkonzentrationen, Temperatur, Zellenzahl – um nur einige zu nennen.

Weblinks

Eugene M. Izhikevich: Equilibrium Artikel in Scholarpedia

Einzelnachweise

Robert Besancon: The Encyclopedia of Physics. Springer Science & Business Media, 2013, ISBN 1-4615-6902-8, S. 406 (eingeschränkte Vorschau in der Google-Buchsuche).
Rolf Haase: Thermodynamik. Springer-Verlag, 2013, ISBN 3-642-97761-8, S. 3 (eingeschränkte Vorschau in der Google-Buchsuche).
Steven H. Strogatz: Nonlinear Dynamics and Chaos. Perseus Books Group, 2001; S. 15.
Bertram Köhler: Evolution und Entropieproduktion. Abgerufen am 9. April 2017.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Robert Besancon: The Encyclopedia of Physics. Springer Science & Business Media, 2013, ISBN 1-4615-6902-8, S. 406 (eingeschränkte Vorschau in der Google-Buchsuche).

[haase-2] Rolf Haase: Thermodynamik. Springer-Verlag, 2013, ISBN 3-642-97761-8, S. 3 (eingeschränkte Vorschau in der Google-Buchsuche).

[3] Steven H. Strogatz: Nonlinear Dynamics and Chaos. Perseus Books Group, 2001; S. 15.

[4] Bertram Köhler: Evolution und Entropieproduktion. Abgerufen am 9. April 2017.