Elastizitätstheorie
Die Elastizitätstheorie beschäftigt sich mit elastischen Körpern wie die Scheibe im Bild und wie ihre Eigenschaften mit einem Materialmodell dargestellt werden können.

Elastizität (altgriechisch ελαστικός elastikos, „anpassungsfähig“) ist die Eigenschaft eines Körpers, unter Krafteinwirkung seine Form zu verändern (Verformung) und wie in der Animation bei Wegfall der einwirkenden Kraft in die Ursprungsform zurückzufedern. Alle Materialien haben einen mehr oder weniger ausgeprägten elastischen Bereich, selbst Keramik, Wasser oder Luft. Hier kündigen sich die beiden Hauptzweige der Elastizitätstheorie an:
- die elastischen Fluide (Flüssigkeiten und Gase), die auf hydrostatischen Druck elastisch reagieren, und
- die elastischen Festkörper, die auch auf einachsigen Zug/Druck und Scherung elastisch antworten.
Als Ursache der Elastizität kommen in Frage:
- Verzerrungen des Atomgitters (bei Metallen)
- das Dehnen von Molekülketten (Gummi und Kunststoffe) oder
- die Änderung des mittleren Atomabstandes (Fluide).
Reale Materialien besitzen eine Elastizitätsgrenze, innerhalb derer sie sich elastisch verformen und jenseits derer dissipative Vorgänge wie viskoses oder plastisches Fließen, Kriechen oder Brüche auftreten. Reale Flüssigkeiten, Gase und manche Feststoffe (wie Eisen und Glas) sind bei schnellen, geringfügigen Volumenänderungen (z. B. Schallwellen) in guter Näherung elastisch. Die Elastizitätsgrenze kann bei Feststoffen bei langsamen und hinreichend kleinen Verformungen eingehalten werden, die in vielen Anwendungen, insbesondere im technischen Bereich, vorliegen. Richtungsabhängigkeiten des Materials wie die Orthotropie von Holz oder materielle Zwangsbedingungen wie Inkompressibilität kommen in der Elastizität, aber auch bei anderem Materialverhalten vor.
Die Gesetze der Mechanik und Thermodynamik geben einen Rahmen vor, in dem sich reale Körper bewegen. Die mathematischen Gleichungen dieser Gesetze treffen keine Aussagen über die individuellen Eigenschaften der Körper und reichen daher nicht aus, die Bewegungen der Körper eindeutig zu bestimmen. Dazu bedarf es noch konstitutiver Gleichungen, die hier die materialspezifische Antwort des Körpers auf eine äußere Kraft beschreiben, ob es also z. B. wegfließt oder sich nur eindrückt.
Die Elastizitätstheorie beschäftigt sich mit der mathematischen Formulierung dieser Beziehung in elastischen Körpern. Sie bildet neben der Theorie des linear-viskosen Fluids die Basis der klassischen Materialtheorie, auf der andere Theorien für Plastizität und Viskoplastizität aufbauen.
Makroskopisches Verhalten
Makroskopisch lassen sich folgende Eigenschaften an einem elastischen Körper beobachten:
- Bei gegebener Verformung (Fluide: Volumenänderung) haben die Reaktionskräfte (der Druck) unabhängig von der Vorgeschichte immer denselben Wert.
- Das Materialverhalten hängt nicht von der Geschwindigkeit der Verformung (Fluide: der Volumenänderung) ab; diese Geschwindigkeit hat also keinen Einfluss auf den Widerstand (Druck), den der Körper der Verformung entgegensetzt.
Diese beiden Merkmale kennzeichnen die Elastizität als eine zeitunabhängige Materialeigenschaft; zusammen mit den folgenden beiden machen sie die Cauchy-Elastizität aus.
- Ist der Ausgangszustand unbelastet, so wird dieser nach jedweder Verformung wieder eingenommen, wenn die Belastungen entfernt werden. Bei elastischen Flüssigkeiten und Gasen ist der Zustand durch das eingenommene Volumen bestimmt, das unter gleichen Bedingungen immer gleich ist.
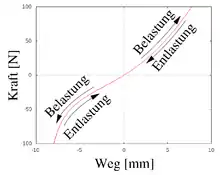
- Im einachsigen Zugversuch erfolgen Be- und Entlastung stets entlang des gleichen Weges, wie im nebenstehenden Bild. Bei Flüssigkeiten und Gasen entspricht das einem Kompressions- und Expansionsversuch.
Wenn zusätzlich noch folgende Eigenschaft vorliegt, ist das Material hyperelastisch:
- Die aufgewendete Verformungsarbeit (Fluide: Kompressionsarbeit) wird vollständig als Verzerrungsenergie im Körper gespeichert, das Material ist also konservativ.
Bei hinreichend kleinen Verformungen ist die Kraft-Weg-Beziehung bei Feststoffen linear, und die Elastizität kann mit Moduln beschrieben werden. Diese Materialeigenschaften quantifizieren das Verhältnis zwischen den Spannungen (Kraft pro Wirkfläche) und den Dehnungen (Verformungsweg pro Abmessung):[1]
- Der Elastizitätsmodul gilt bei einachsigem Zug; hier tritt nicht nur in Zugrichtung eine Verformung auf, sondern auch quer dazu, was die dimensionslose Querdehnzahl quantifiziert.
- der Schubmodul gilt bei Scherung
- der Kompressionsmodul gilt bei allseitigem Zug/Druck.
Die vollständige Beschreibung
- der isotropen linearen Elastizität benötigt zwei der genannten Größen (ein Elastizitätsmodul und eine Querdehnzahl)
- der kubischen Anisotropie benötigt drei Größen (ein Elastizitätsmodul, eine Querdehnzahl und ein Schubmodul)
- der transversalen Isotropie benötigt bereits fünf Größen (zwei Elastizitätsmoduln, zwei Querdehnzahlen und einen Schubmodul)
- der Orthotropie benötigt neun Größen (je drei Elastizitätsmoduln, Querdehnzahlen und Schubmoduln).
Maximal werden 21 Parameter benötigt, um einen realen linear elastischen Stoff zu beschreiben, siehe den Abschnitt #Materialmodelle der Hyperelastizität.
Kontinuumsmechanische Theorie
Cauchy-Elastizität
Die vier im vorigen Kapitel als erstes genannten Eigenschaften bestimmen die Cauchy-Elastizität. Bei ihr hängen die Spannungen, d. h. der Widerstand gegen Verformung, ausschließlich von der gegenwärtigen Verformung und evtl. von Anfang an vorkommenden Eigenspannungen ab, nicht aber von der Vorgeschichte oder der Geschwindigkeit der Verformung.
Außerdem sind bei Cauchy-Elastizität die Verformungen (innerhalb der Elastizitätsgrenze) reversibel, d. h. der Körper kann durch eine Kraft verformt werden, aber nach Wegnahme der Kraft federt er wieder in den ursprünglichen Zustand zurück.
Bei allgemeiner, anisotroper, linearer Elastizität kann der Zusammenhang zwischen den sechs Spannungen und den sechs Dehnungen mit maximal 36 Proportionalitätskonstanten dargestellt werden.
Bezugssysteminvarianz
Ein bewegter Beobachter misst immer dasselbe Materialverhalten wie ein ruhender, was sich im Prinzip der materiellen Objektivität niederschlägt. An der Cauchy-Elastizität können bereits die Bedingungen festgestellt werden, unter denen Materialgleichungen bezugssysteminvariant oder genauer, invariant gegenüber einer euklidischen Transformation des Bezugssystems eines Beobachters sind. Materialgleichungen für elastische Fluide sind automatisch bezugssysteminvariant. Bei Feststoffen wird diese Forderung dadurch genüge getan, dass die Materialgleichungen zwischen Spannungen und Dehnungen in der lagrangeschen Fassung aufgestellt werden.
Elastische Fluide
Fluide unterscheiden sich aus kontinuumsmechanischer Sicht von Feststoffen dadurch, dass sich in ihnen der Spannungszustand bei beliebigen, volumenerhaltenden Verformungen nicht ändert (ihre Symmetriegruppe bilden die unimodularen Tensoren aus der speziellen linearen Gruppe). In elastischen Fluiden wirkt nur eine Spannungskomponente, der Druck; Schubspannungen dagegen, wie sie in viskosen Fluiden oder Feststoffen auftreten können, sind in ihnen ausgeschlossen oder vernachlässigbar klein.
Zu den elastischen Fluiden gehören die ideale Flüssigkeit, das ideale Gas und das reibungsfreie reale Gas. Viele Materialgleichungen der elastischen Gase nennen sich Zustandsgleichung, was unterstreicht, dass der Druck in ihnen unter gleichen Bedingungen immer gleich ist und sie somit Cauchy-elastisch sind. Der Druck hängt kinematisch nur von der augenblicklichen Volumendehnung oder Dichte ab.
Einen wichtigen Spezialfall stellen die barotropen Fluide dar, in denen die Dichte ausschließlich eine Funktion des Drucks ist. Die so modellierten barotropen, elastischen Fluide sind automatisch isotrop, bezugssysteminvariant und konservativ oder – anders ausgedrückt – hyperelastisch.
Bewegungsgleichungen
Die Bewegungsgleichung der elastischen Fluide sind die Euler’schen Gleichungen der Strömungsmechanik.
Ein wichtiger Spezialfall liegt vor, wenn die Flüssigkeit barotrop, die Volumenkraft (u. a. die Schwerkraft) konservativ und das Geschwindigkeitsfeld stationär ist. Dann führt die Integration der Euler-Gleichungen entlang einer Stromlinie auf die Bernoulli’sche Energiegleichung, die technische Rohrströmungen gut beschreibt.
Wenn das Geschwindigkeitsfeld zusätzlich rotationsfrei ist, dann liegt eine Potentialströmung vor, in der die Bernoulli’sche Energiegleichung nicht nur entlang von Stromlinien gilt, sondern zwischen zwei beliebigen Punkten gilt. Potentialströmungen können mit analytischen Mitteln mathematisch exakt berechnet werden.
Thermodynamische Konsistenz
Obwohl die Reaktionskräfte in einem Cauchy-elastischen Material vom zurückgelegten Verformungsweg unbeeinflusst sind, kann bei Feststoffen die auf verschiedenen Verformungswegen (mit gleichem Start- und Endpunkt) geleistete Formänderungsarbeit unterschiedlich groß ausfallen. Dies steht in Abwesenheit eines Dissipationsmechanismus im Widerspruch zu thermodynamischen Prinzipien.
Wegunabhängigkeit auch der Formänderungsarbeit hingegen führt zur thermodynamisch konsistenten Hyperelastizität, einem Spezialfall der Cauchy-Elastizität.
Hyperelastizität
Hyperelastische Stoffe sind Cauchy-elastisch und zusätzlich konservativ. Die Formänderungsarbeit ist bei Hyperelastizität wegunabhängig, und die Spannungen stehen in einer Potenzialbeziehung zu den Dehnungen. Das Potenzial ist bei Feststoffen die Helmholtz’sche freie Energie, aus der sich gemäß der Clausius-Duhem-Ungleichung in isothermen Prozessen die Spannungen durch Ableitung nach den Dehnungen berechnen.
Es kann gezeigt werden, dass hyperelastische Materialien genau dann isotrop und bezugssysteminvariant sind, wenn die Helmholtz’sche freie Energie eine Funktion der Änderung von materiellen Volumen-, Flächen- und Linienelementen bei einer Deformation ist.[2]
Konservativität
Die Wegunabhängigkeit der Formänderungsarbeit drückt sich dadurch aus, dass die Formänderungsarbeit nur vom Start- und Endpunkt des Verformungsweges, nicht aber von dessen Verlauf abhängt. Im Spezialfall der Übereinstimmung von Start- und Endpunkt ergibt sich: Entlang eines geschlossenen Verformungsweges wird keine Arbeit verrichtet oder Energie verbraucht; aufgewandte Arbeiten werden vom Körper bis zur Rückkehr zum Ausgangspunkt vollständig zurückgegeben. Die Konservativität folgt hier auch daraus, dass die Verformungsleistung exakt die Rate der Formänderungsenergie ist, aufgewandte Arbeiten also vollständig (dissipationslos) in Formänderungsenergie umgesetzt werden.
Materialmodelle der Hyperelastizität
Für isotrope Feststoffe liegen eine Reihe von Materialmodellen vor, mit denen sich reale, reversible und große Verformungen in guter Näherung nachbilden lassen. Das einfachste dieser Modelle ist das Hooke’sche Gesetz für lineare Elastizität, dass jedwedes Materialmodell der Hyperelastizität bei kleinen Deformationen in erster Ordnung approximiert. Eine Approximation zweiter Ordnung bei inkompressiblem Material stellt das Mooney-Rivlin-Modell dar. Das Neo-Hooke-Modell, ein Spezialfall dieses Modells, verallgemeinert das Hooke’sche Gesetz in geeigneter Weise auf große Deformationen, für die es ansonsten ungeeignet ist.
Der Elastizitätstensor ergibt sich in der Hyperelastizität aus der zweiten Ableitung der Formänderungsenergie nach den Dehnungen. Weil die Reihenfolge der Ableitungen vertauschbar ist, ist der Elastizitätstensor symmetrisch und sind von den 36 Materialparametern in der linearen Cauchy-Elastizität nur 21 in der Hyperelastizität unabhängig; ein linear-hyperelastisches Material kann daher mit maximal 21 Parametern beschrieben werden.
Lineare isotrope Hooke’sche Elastizität von Feststoffen
In diesem Abschnitt wird neben der linearen Elastizität auch kinematische Linearität vorausgesetzt, was bei kleinen Verformungen von Festkörpern vorliegt.
Navier-Cauchy-Gleichungen
Die lokale Impulsbilanz ist eine Gleichung, in der nur die Spannungen, die Beschleunigung und die Schwerkraft auftreten. Nun können die Spannungen über das Hooke’sche Gesetz mit den Dehnungen und diese wiederum mit den Verschiebungen ausgedrückt werden, was auf die Navier-Cauchy-Gleichungen führt. Diese enthalten Wellengleichungen als Lösung für longitudinale, primäre weil schneller laufende P-Wellen und transversale, sekundäre weil langsamer laufende S-Wellen. Im Fall einer harmonischen Schwerkraft ist das Verschiebungsfeld eine Biharmonische Funktion.
Satz von Clapeyron
- Die Arbeit
- der auf der Oberfläche a eines Körpers angreifenden
- Kräfte
plus
- die Arbeit
- der im Volumen v des Körpers wirkenden
- Volumenkraft ,
jeweils am Verschiebungsfeld ,
ist gleich
- der Arbeit
- des Spannungsfeldes , das die Gleichgewichtsbedingung erfüllt,
- an den aus den Verschiebungen resultierenden Verzerrungen :
Dieser Satz von Clapeyron setzt hinreichende Glattheit und Stetigkeit der Felder voraus.[3]
In einem linear elastischen Körper ist das Produkt aus den Spannungen und den Dehnungen die halbe Formänderungsarbeit.
Sind die äußeren Kräfte konservativ, dann folgt das
Prinzip vom Minimum der potentiellen Energie und der Ergänzungsenergie
Das Prinzip vom Minimum der potentiellen Energie besagt, dass von allen Verschiebungsfeldern, die bestimmte Randbedingungen in einem von konservativen äußeren Kräften belasteten, elastischen Festkörper erfüllen, diejenigen Verschiebungen, die die Gleichgewichtsbedingungen erfüllen, die potentielle Energie minimieren. (Die potentielle Energie ist die Summe aus den Arbeiten der konservativen, äußeren Kräfte und der Formänderungsenergie.)
Das Prinzip vom Minimum der Ergänzungsenergie besagt, dass in einem elastischen Festkörper von allen Spannungszuständen, die die Randbedingungen erfüllen, derjenige Zustand, der die Gleichgewichtsbedingung erfüllt, die Ergänzungsenergie minimiert.
Die spezifische Ergänzungsenergie Uc und die spezifische Formänderungsenergie U stehen im Zusammenhang
Satz von Betti
Wird ein linear hyperelastischer Körper äußeren Kräften ausgesetzt, so ergibt sich daraus eine Deformation, welche die Formänderungsenergie minimiert. Das System aus Spannungen, Dehnungen und Verschiebungen ist ein elastischer Zustand des Körpers, der zum angreifenden Kraftsystem gehört.
Liegt ein zweites Kraftsystem vor, das einen zweiten elastischen Zustand hervorruft, dann gilt der Satz von Betti:
- Die Arbeit des ersten Kraftsystems an den Verschiebungen des zweiten elastischen Zustandes ist gleich der Arbeit des zweiten Kraftsystems an den Verschiebungen des ersten elastischen Zustandes.
Diese reziproken Arbeiten der äußeren Kräfte entsprechen reziproken Formänderungsarbeiten:
- Die Arbeit der Spannungen des ersten elastischen Zustandes an den Dehnungen des zweiten elastischen Zustandes ist gleich der Arbeit der Spannungen des zweiten elastischen Zustandes an den Dehnungen des ersten elastischen Zustandes.
Der Satz von Betti ist eine Grundlage der Randelementmethode.
Kompatibilitätsbedingungen
Bei der Bewegung eines Körpers durch den Raum treten in den für die Kontinuumsmechanik interessanten Fällen Verformungen auf, die sich durch die Verzerrungen quantifizieren lassen. Von den Verzerrungen gibt es im Allgemeinen dreidimensionalen Fall sechs Komponenten. Sollen aus ihnen die drei Komponenten der Bewegung (d. h. die Verschiebungen) in den drei Raumrichtungen rekonstruiert werden, so können die Verzerrungen nicht voneinander unabhängig sein; stattdessen müssen sie die für sie formulierten Kompatibilitätsbedingungen einhalten. Indem die Verzerrungen im linear elastischen Material mit den Spannungen ausgedrückt werden, entstehen entsprechende Kompatibilitätsbedingungen für die Spannungen.
In der linearen Elastizität sind die Kompatibilitätsbedingungen mit vertretbarem Aufwand erfüllbar und eröffnen so die Möglichkeit, ein Randwertproblem mit Spannungsfunktionen zu lösen.
Spannungsfunktionen
Im Gleichgewicht kommen in der lokalen Impulsbilanz nur die Spannungen und die Schwerkraft vor. Hier können die Spannungen als primäre Unbekannte gewählt und mit Spannungsfunktionen ausgedrückt werden, welche die Gleichgewichtsbedingungen automatisch einhalten. So reduziert sich die Lösung eines Randwertproblems auf das Auffinden von Spannungsfunktionen, die die vorliegenden Randbedingungen und die Kompatibilitätsbedingungen für die Spannungen erfüllen.
Besonders gut untersucht ist der ebene Fall mit der Airy’schen Spannungsfunktion, mit deren Hilfe heute analytische Lösungen vieler Randwertaufgaben in der Ebene vorliegen.
Mathematische Theorie
Ein reales Material deformiert sich unter Krafteinwirkung so, dass die Formänderungsenergie minimiert wird. Die mathematische Elastizitätstheorie untersucht u. a. die Frage, unter welchen Bedingungen auch im mathematischen Modell eine Deformation existiert, welche die Formänderungsenergie minimiert.
Eine in diesem Zusammenhang wichtige und plausible Forderung an die Formänderungsenergie ist, dass sie bei unendlich großer Deformation gegen unendlich strebt, die Formänderungsenergie also eine koerzitive Funktion der Deformation ist. Wenn die Formänderungsenergie nämlich eine koerzitive und konvexe Funktion der Deformation ist, dann existiert gewiss eine die Formänderungsenergie minimierende Deformation.
Wenn die Formänderungsenergie auch über alle Grenzen wächst, wenn der Körper auf null Volumen zusammengedrückt wird, was plausibel ist, dann kann sie nicht konvex sein. Daher ist Konvexität eine unhaltbare Forderung an die Formänderungsenergie.
Dagegen garantieren die Polykonvexität nach John M. Ball[4] und Koerzitivität der Formänderungsenergie die Existenz einer die Formänderungsenergie minimierenden Deformation:
- für isotrope Hyperelastizität liegt eine Reihe solcher Formänderungsenergiefunktionen vor, die polykonvex und koerzitiv sind.[5]
- für den Fall anisotroper Hyperelastizität stellte J. M. Ball die Frage:[6] „Are there ways of verifying polyconvexity […] for a useful class of anisotropic stored-energy functions?“ (zu Deutsch: „Gibt es Wege, die Polykonvexität […] für eine nützliche Klasse anisotroper Formänderungsenergiefunktionen nachzuweisen?“) Die Suche nach der Antwort auf diese Frage ist noch im einundzwanzigsten Jahrhundert Gegenstand reger Forschungsaktivität.
Siehe auch
Einzelnachweise und Fußnoten
- Weil die aufzuwendende Kraft und der zurückgelegte Weg bei einer Deformation maßgeblich von den Dimensionen des Körpers abhängen, wird die Kraft auf ihre Wirkfläche bezogen (ergibt die Spannung) und der Weg auf eine geeignete Abmessung des Körpers (ergibt die Dehnung).
- P. G. Ciarlet (1988), Theorem 4.4-1, siehe auch Strecktensor#Hauptinvarianten des rechten Cauchy-Green Tensors.
- M.E. Gurtin (1972), S. 60, Martin H. Sadd: Elasticity – Theory, applications and numerics. Elsevier Butterworth-Heinemann, 2005, ISBN 0-12-605811-3, S. 110.
- J. M. Ball: Convexity conditions and existence theorems in non-linear elasticity. In: Archive for Rational Mechanics and Analysis, 63, 1977, S. 337–403 und
J. M. Ball: Constitutive inequalities and existence theorems in nonlinear elasto-statics. In: R. J. Knops (Hrsg.): Herriot Watt Symposion: Nonlinear Analysis and Mechanics, Band 1. Pitman, London 1977, S. 187–238, ISBN 0-273-01128-6; ISBN 0-273-08461-5. - S. Hartmann und P. Neff: Polyconvexity of generalized polynomial type hyperelastic strain energy functions for near incompressibility. In: International Journal of Solids and Structures 40 (2003), S. 2767–2791.
- J. M. Ball: Some open problems in elasticity. In: P. Newton, P. Holmes (2002), S. 3–59.
Literatur
- H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.
- M. Bestehorn: Hydrodynamik und Strukturbildung. Springer, 2006, ISBN 978-3-540-33796-6.
- P. G. Ciarlet: Mathematical Elasticity – Volume I: Three-Dimensional Elasticity. North-Holland, 1988, ISBN 0-444-70259-8.
- P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2000, ISBN 3-540-66114-X.
- G. A. Holzapfel: Nonlinear Solid Mechanics: A Continuum Approach for Engineering. Wiley, 2000, ISBN 978-0-471-82319-3.
- J. E. Marsden und J. R. Hughes: Mathematical Foundations of Elasticity. Prentice Hall, 1983, ISBN 978-0-486-67865-8.
- Paul Newton, Philip Holmes (Hrsg.): Geometry, Mechanics and Dynamics. Springer, 2002, ISBN 978-0-387-95518-6.
- M. Silhavy: The Mechanics and Thermodynamics of Continuous Media. Springer, 1997, ISBN 978-3-540-58378-3.
- M. E. Gurtin: The Linear Theory of Elasticity. In: S. Flügge (Hrsg.): Handbuch der Physik. Band VI2/a, Bandherausgeber C. Truesdell. Springer, 1972, ISBN 3-540-05535-5.
- Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium, Ernst & Sohn, Berlin 2018, ISBN 978-3-433-03229-9.