Spannungszustand
Der Spannungszustand ist die Gesamtheit aller denkbaren Spannungsvektoren in einem materiellen Punkt in einem belasteten Körper[1]. Der Spannungszustand definiert den Spannungsvektor, der auf einer Fläche wirkt, in eindeutiger Weise.

Spannungsvektoren sind Vektoren mit der Dimension Kraft pro Fläche und entstehen immer, wenn Kräfte auf Körperflächen eingeleitet werden. Die Spannungen in den Krafteinleitungsstellen pflanzen sich dem Kraftfluss folgend im Körper – abseits von Behinderungen stetig – fort und bilden in jedem Partikel des Körpers einen Spannungszustand aus. Um ein Partikel abseits von Störstellen kann man sich eine (infinitesimal) kleine Kugel vorstellen, in der überall derselbe Spannungszustand wie im Partikel herrscht, und diesen Spannungszustand wie im Bild visualisieren. Die Spannungsvektoren setzen sich aus Normalspannungen (radial im Bild) und Schubspannungen (tangential im Bild) zusammen. Der Spannungstensor fasst den Spannungszustand zu einem mathematischen Objekt zusammen.
Der Körper kann starr, fest, flüssig oder gasförmig sein. Der Spannungszustand ist im Allgemeinen eine Funktion der Zeit und dem Ort im Körper und bildet sich aus abhängig von dessen Form, Belastung (Druck, Scherung und bei Festkörpern zusätzlich Zug, Biegung, Torsion), Materialeigenschaften und geometrischen Bindungen.
Definition
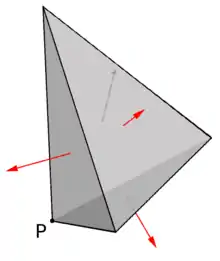
Drei Spannungsvektoren in einem Punkt auf drei verschiedenen Ebenen, deren Flächennormalen linear unabhängig sind, definieren den Spannungszustand in dem Punkt vollständig.[2]
Denn wenn auf einer vierten Ebene durch den Punkt, im Folgenden P genannt, der Spannungsvektor gesucht wird, dann ergibt sich dieser wie folgt in eindeutiger Weise aus den drei bekannten. Die vierte Ebene werde dazu ein infinitesimales Stück vom Punkt P weg parallelverschoben, wodurch die vier Ebenen einen Tetraeder aus dem Körper ausschneiden, siehe Bild. Der Tetraeder sei so klein, dass in seinem Raumbereich der Spannungszustand gleichförmig ist. Dann bilden die mit ihrer Tetraederfläche multiplizierten Spannungsvektoren Kräfte, die mit der Kraft auf der vierten Fläche im Gleichgewicht sein müssen, denn Volumeneffekte (Erdbeschleunigung, Magnetismus, …) streben beim infinitesimal kleinen Tetraeder als volumenproportionale Größen gegenüber den flächenproportionalen Kräften der Spannungsvektoren gegen Null. Damit ist die Kraft auf der vierten Seite eindeutig bestimmt. Rein geometrisch ist aber auch aus drei Tetraederflächen die vierte Fläche nach Inhalt und Normaleneinheitsvektor eindeutig bestimmt und folglich der Spannungsvektor auf der Fläche. Weil im Raumbereich des Tetraeders der Spannungszustand gleichförmig ist, wirkt dieser Spannungsvektor auch auf der vierten Ebene durch P.
Eine genaue Analyse zeigt, dass deshalb der Zusammenhang zwischen den Flächennormalen und den Spannungsvektoren ein linearer sein muss, was die Aussage des Cauchy’schen Fundamentaltheorems ist, mit dem Augustin-Louis Cauchy den Spannungstensor als linearen Operator zwischen den Normaleneinheitsvektoren und den Spannungsvektoren einführte.
Grad des Spannungszustands
Der Grad des Spannungszustands wird von der Anzahl der nicht verschwindenden Hauptspannungen bestimmt.
Unter einaxialem oder uniaxialem Zug bzw. Druck kann sich ein einachsiger Spannungszustand ausbilden, mit von null verschiedener Hauptspannung in Belastungsrichtung und verschwindenden Hauptspannungen senkrecht dazu. Auf Zug belastete, lange, schlanke, homogene Stäbe oder Seile weisen abseits von der Lasteinleitungszonen in guter Näherung einen einachsigen Spannungszustand auf.
Bei biaxialem Zug herrscht ein zweiachsiger oder ebener Spannungszustand (zwei Hauptspannungen in den Belastungsrichtungen, die dritte Hauptspannung senkrecht zur Ebene ist null). An unbelasteten Teilen der Oberfläche eines Körpers herrschen ebene Spannungszustände. Mehr dazu findet sich unten.
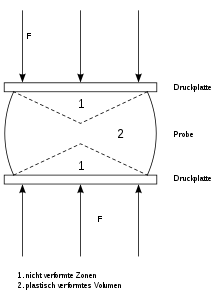
In unregelmäßig geformten Bauteilen/Proben (Bsp.: ISO-V-Probe aus Kerbschlagbiegeversuch), in Krafteinleitungsstellen, bei ungleichförmiger Belastung oder bei Querdehnungsbehinderung wie im Bild treten meist dreiachsige, räumliche Spannungszustände mit drei nicht verschwindenden Hauptspannungen auf.
Spezialfälle
Hydrostatischer Spannungszustand
Der hydrostatische Spannungszustand ist ein räumlicher Spannungszustand, der sich bei allseitigem Zug/Druck ausbildet, was bei Windstille auf der Erde allgegenwärtig ist. Der hydrostatische Druck der Erdatmosphäre erzeugt diesen Spannungszustand in allen ansonsten unbelasteten Körpern. Die Spannungsvektoren sind in jeder Schnittebene parallel zu ihrer Normale, es treten in keiner Ebene Schubspannungen auf, und alle Hauptspannungen sind gleich. Hydrostatischem Druck kann von Materialien in hohem Maß ohne bleibende Verformungen standgehalten werden.
Ebener Spannungszustand
Ebene Spannungszustände kommen bei biaxialem Zug oder an unbelasteten Teilen der Oberfläche von Körpern vor. Genauso kann auch in dünnen Schalen, Flugmembranen oder Flächentragwerken fernab von Krafteinleitungsstellen oder anderen Störstellen von einem ebenen Spannungszustand ausgegangen werden. Er kann anschaulich durch den Mohr’schen Spannungskreis dargestellt werden.
An unbelasteten Teilen der Körperoberfläche sind die Bedingungen des ebenen Spannungszustands exakt erfüllt, denn die Schnittreaktion entfällt dort in der Tangentialebene an die Oberfläche nach Voraussetzung. Im Körperinneren kann ein ortsabhängiger Spannungszustand bei einer Poissonzahl ungleich null nur näherungsweise ein ebener sein. Denn die vom Spannungszustand verursachten Dehnungen in der Ebene bewirken senkrecht zur Ebene ebenso ortsabhängige Querkontraktionen des Körpers, in dem nun Scherungen senkrecht zur Ebene auftreten. Diese Scherungen gehen im Allgemeinen aber mit entsprechenden, senkrecht zur Ebene wirkenden Schubspannungen einher. Nur wenn diese vernachlässigbar klein sind, kann noch von einem ebenen Spannungszustand gesprochen werden.
Homogener Spannungszustand
Der homogene Spannungszustand ist ein ortsunabhängiger Spannungszustand. In einem homogenen Spannungszustand wird das Tragverhalten eines Materials optimal ausgenutzt.
In einem ebenso homogenen Material stellt sich ein ebenso homogener Verzerrungszustand ein. Die Dehnung kann dann mit Dehnungsmessstreifen, Messkameras oder Messarmen bestimmt werden, die makroskopische Messapparaturen sind. Wenn im betrachteten Raumbereich ein homogener Zustand vorliegt, liefert die gemessene Dehnung einen direkt interpretierbaren Wert für die Dehnung der Probe. Entsprechend ist der homogene Spannungszustand in der Materialtheorie und der Messtechnik von hervorragender Bedeutung.
In diesem Zusammenhang ist die universale Deformation nützlich, die bei beliebigem homogenem Material durch ausschließlich oberflächlich eingeleitete Spannungen hervorgerufen werden kann.[3] Eine universale Deformation mit homogenem Spannungszustand wird bei ein- oder mehraxialem Zug, insbesondere hydrostatischem Druck, bei Scherung oder Torsion geschaffen.
Der homogene Spannungszustand ist eine Idealisierung, die in realen Körpern kaum zu finden ist. Denn viele Körper besitzen Störstellen, Lunker, Haarrisse oder Kerben. Auch Materialgrenzen, Krafteinleitungsstellen oder Bereiche mit Eigenspannungen weisen in ihrer Nähe inhomogene Spannungszustände auf. Diese bewirken inhomogene Dehnungen, die z. B. bei Eigenspannungsbestimmung durch Freibohren ersichtlich werden. Mathematischen Methoden helfen diese Dehnungen zu interpretieren und auszuwerten. Nach dem Prinzip von St. Venant klingt die Störung mit zunehmender Entfernung ab und stellt sich ein homogener Spannungszustand ein.
Spannungszustände in Flächenträgern
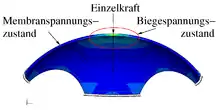
Das Bild zeigt eine Kuppelschale, die in ihrer Mitte mit einer Einzelkraft belastet wird. Fernab der Krafteinleitung liegt der Membranspannungszustand vor (blau im Bild). In der Umgebung der Krafteinleitung, die eine Störstelle ist, liegt ein Biegespannungszustand vor (grün).
Unter bestimmten Voraussetzungen werden in einer Schale die Belastungen vorrangig durch über die Wandstärke konstant verteilte und zur Schalenmittelfläche parallele Spannungen zu den Stützen hin abgeleitet. In solchen Fällen wird von einem Dehnspannungs- oder Membranspannungszustand gesprochen, der auch im Scheibenspannungszustand ebener Flächentragwerke vorliegt, siehe Scheibentheorie. Im Membranspannungszustand wird das Tragverhalten des Materials optimal ausgenutzt. Der Membranspannungszustand bildet sich fernab von Krafteinleitungsstellen und anderer Störstellen aus.
In der Nähe von Störstellen kommt es bei Schalen zum ungünstigeren Biegespannungszustand. In der Umgebung der Störstelle entstehen über die Schalendicke variierende Biegespannungen und Schubspannungen senkrecht zur Schalenmittelfläche. Nach dem Prinzip von St. Venant klingen die Störungen aber mit dem Abstand zur Störstelle rasch ab. Der Biegespannungszustand kann mit dem Plattenspannungszustand ebener Flächentragwerke verglichen werden, siehe Plattentheorie.
Anwendung in der Festigkeitslehre
Der Spannungszustand kann zur Charakterisierung von Verformungen in Bauteilen herangezogen werden, wobei Dehnungen dann auch noch eine Rolle spielen. Der Spannungszustand eignet sich insbesondere für Festigkeitsbetrachtungen in isotropen elastischen Festkörpern, wobei oft die Kenntnis einer oder mehrerer Spannungen im Querschnitt eines Bauteils an einer bestimmten Stelle oder an mehreren bestimmten Stellen für Rückschlüsse an anderer Stelle im gleichen Bauteil heranzuziehen versucht wird. Solche Festigkeitsbetrachtungen sind Gegenstand der Elastizitäts- und der Plastizitätstheorie. Die Verformungen verursachen Spannungen und können durch Festigkeitsberechnungen oftmals systematisch ermittelt werden. Eine häufig verwendete Vorgehensweise ist dabei die, dass man die räumlichen Spannungszustände an einem aussagekräftigen Punkt in einem belasteten Bauteil ermittelt, indem man Dehnungen am Bauteil mit Dehnungsmessstreifen-Messtechnik misst, diese über bestimmte Rechnungen in einen Spannungstensor einbringt und anschließend durch Hauptachsentransformation extremale Spannungen ermittelt.
Einzelnachweise
- H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5, S. 142.
- H. Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5.
- C. Truesdell: Die Nicht-Linearen Feldtheorien der Mechanik. In: S. Flügge (Hrsg.): Handbuch der Physik. Band III/3. Springer, 2013, ISBN 978-3-642-46017-3, S. 184 (englisch).
Literatur
- Hans Göldner, Franz Holzweißig: Leitfaden der Technischen Mechanik: Statik, Festigkeitslehre, Kinematik, Dynamik. 11. verb. Auflage. Fachbuchverlag, Leipzig 1989, ISBN 3-343-00497-9
- Eduard Pestel, Jens Wittenburg: Technische Mechanik. Band 2: Festigkeitslehre. 2. überarb. und erw. Auflage. Bibliographisches Institut, Mannheim 1992, ISBN 3-411-14822-5