Mechanische Spannung

Die mechanische Spannung (Formelzeichen $\sigma$ (kleines Sigma) und $\tau$ (kleines Tau), englisch stress, französisch contrainte) ist ein Maß für die innere Beanspruchung eines Körpers infolge dessen Belastung von außen. Da innerhalb der Mechanik keine Verwechslungsgefahr mit der elektrischen Spannung besteht, wird sie kurz als Spannung bezeichnet.

Physikalische Größe

Name

mechanische Spannung

Formelzeichen

$\sigma$ (Normalspannungen),
$\tau$ (Schub- oder Scherspannungen)

Größen- und Einheitensystem	Einheit	Dimension
SI	Pascal; Pa = N/m²	M·L⁻¹·T⁻²

Siehe auch: Druck

p

Die mechanische Normal-Spannung $\sigma$ auf einer gedachten Schnittfläche $A$ (engl. area) durch einen Körper ist die auf sie bezogene senkrecht auf sie wirkende Komponente $F_{n}$ einer äußeren Kraft $F$ (engl. force):[1]

\sigma =\lim _{\Delta A\to 0}{\frac {\Delta F_{n}}{\Delta A}}

.

Die Definition des Spannungsbegriffs geht auf Cauchy (1823) zurück.[2]

Die mechanische Schub- oder Scherspannung $\tau$ in einer gedachten Schnittfläche $A$ durch einen Körper ist die auf sie bezogene in ihr verlaufende Komponente $F_{A}$ (Querkraft) einer äußeren Kraft $F$ :

\tau ={\frac {F_{A}}{A}}

, (Näherungsgleichung: Schubspannung ist über Fläche nicht konstant und am Flächenrand immer null).

Die mechanische Spannung ist von derselben physikalischen Größenart wie der Druck, nämlich Kraft pro Fläche. In ruhenden Flüssigkeiten und Gasen ist Druck eine in allen Raumrichtungen gleichermaßen wirkende Normalspannung.

Im Maschinen- und konstruktiven Ingenieurbau erfordert die Dimensionierung von Objekten die Kenntnis der auftretenden mechanischen Spannungen. Als Komponenten des Spannungstensors kommen die mechanischen Spannungen in physikalischen Gesetzen vor.

Schnittspannungen

Durch Anwendung des Schnittprinzips können innere Spannungen eines Körpers anschaulich dargestellt werden. An einem gedanklichen Schnitt an beliebiger Stelle eines Körpers werden die Schnittkräfte angetragen, die aus den von außen auf den Körper wirkenden Kräften resultieren und auf die inneren Beanspruchungen des Körpers schließen lassen.

Normal-, Biege-, Schub-, Torsionsspannung und wahre Spannung

Bei einer gleichförmigen Zug- oder Druckbelastung eines Stabes ist die Spannung über die Querschnittsfläche gleichmäßig verteilt. Die Normalspannung, d. h. die Spannung bei Normalkraftbeanspruchung durch Zug oder Druck, ergibt sich aus

\sigma _{N}={\frac {F}{A}},

wobei $F=F_{\perp }$ die Kraft in Richtung der Flächennormale und $A$ der Flächeninhalt des Stabquerschnitts ist. Bei den wahren Spannungen ist dies der Flächeninhalt beim verformten Stab und bei den Nenn- oder Ingenieursspannungen der Nennwert des undeformierten Ausgangsstabquerschnitts, siehe Zugversuch. Der Spannungstensor hat immer 3 (für alle drei Raumrichtungen) Normalspannungskomponenten, ist diese in eine Raumrichtung positiv, liegt in dieser Raumrichtung Zug vor, ebenso bei Druckspannungen ist dann die Normalspannungskomponente in diese Richtung negativ.

Bei einer Biegebelastung des Stabes ergibt sich eine Biegespannung, die am Rand des Stab-Querschnitts am höchsten ist (in der sogenannten Randfaser) und zur Mitte hin auf Null abnimmt (in der sogenannten neutralen Faser). Als Biegespannung wird zusammenfassend die durch die Biegung jeweils in einem Teil des Querschnitts hervorgerufene Druck- und Zugspannung bezeichnet:

\sigma _{B}(x,y,z)=-{\frac {M_{z}(x)\cdot I_{y}+M_{y}\cdot I_{yz}}{I_{y}(x)\cdot I_{z}(x)-(I_{yz})^{2}}}\cdot y+{\frac {M_{y}(x)\cdot I_{z}(x)+M_{z}(x)\cdot I_{yz}}{I_{y}(x)\cdot I_{z}(x)-(I_{yz})^{2}}}\cdot z

[3]

Bei konstanter einachsiger Biegung $M_{y}(x)=M_{y}$ im Hauptträgheitsachsensystem vereinfacht sich die Formel zu:

\sigma _{B}(z)={\frac {M_{y}}{I_{yy}}}\cdot z\quad {\text{und}}\quad |\sigma _{B}|_{\mathrm {max} }={\frac {|M_{y}|}{|W_{y}|_{\mathrm {min} }}}\quad {\text{mit}}\quad W_{y,{\text{positiv}}}={\frac {I_{yy}}{z_{\mathrm {max} }}}\quad {\text{und}}\quad W_{y,{\text{negativ}}}={\frac {I_{yy}}{z_{\mathrm {min} }}},

wobei $M_{y}$ das Biegemoment um die y-Achse, $I_{yy}$ das Flächenträgheitsmoment um die y-Achse, $z$ der Abstand von der neutralen Faser (bei σ_B = 0), $z_{R}$ der maximal oder minimale auftretende Abstand der Schwerachse zur Randfaser und $W$ das Widerstandsmoment ist, siehe Balkentheorie. Die folgende Skizze verdeutlicht dies an einem Kragträger:

Spannungen in Kragträger

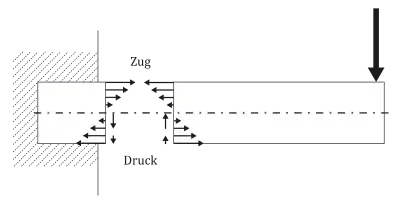
Als Vektor hat der Schnittspannungsvektor drei Komponenten, die von der Orientierung der Schnittfläche abhängen. Die senkrechten Pfeile an den Schnittufern deuten durch die Querkraft eingeleitete Schubspannungen an. Bei einem mit einer Querkraft belasteten Profil wie im Bild stellt sich ein nicht konstanter Schubspannungsverlauf über den Querschnitt ein. Greift die Querkraft außerhalb des Schubmittelpunktes an, tritt zusätzlich Torsion auf.

Bei der Torsion von Stäben mit Kreis(ring)querschnitt lautet die Schubspannung:

\tau ={\frac {M_{t}}{I_{p}}}r\quad {\text{und}}\quad \tau _{\mathrm {max} }={\frac {M_{t}}{W_{t}}}\quad {\text{mit}}\quad W_{t}:={\frac {I_{p}}{r_{a}}}

Darin ist M_t das Torsionsmoment, I_p das polare Flächenträgheitsmoment, W_t das Torsionswiderstandsmoment, r die radiale Zylinderkoordinate und r_a der Außenradius des (Hohl-)Zylinders.[4]

Die Formeln zur Biege- und Torsionsspannung setzen lineare Elastizität voraus.

Die Tensorrechnung erlaubt, den Spannungszustand zunächst unabhängig von einem bestimmten Koordinatensystem zu beschreiben und erst nach einer Herleitung des jeweiligen Berechnungsverfahrens (wie obige Formeln) den geometrischen Eigenschaften des Körpers anzupassen, beispielsweise in Zylinderkoordinaten wie bei der Torsion.

Spannungsvektoren und Spannungstensor

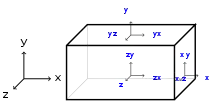
Quader mit mechanischen Spannungen

Die an einer bestimmten Stelle wirkenden Spannungen werden in ihrer Gesamtheit durch die Spannungen in drei Schnittflächen beschrieben, die sich an der Stelle kreuzen, also durch drei Spannungsvektoren mit je drei spannungsartigen Komponenten. Die drei Spannungsvektoren bilden zusammengenommen den von Augustin-Louis Cauchy definierten Spannungstensor. Die Ausrichtung der Schnittflächen ist dabei beliebig, solange ihre Normalen linear unabhängig sind, denn als Tensor ist der Spannungstensor unabhängig vom gewählten Basissystem. Beispielhaft kann man die drei Schnittflächen jeweils senkrecht zu einer Richtung eines kartesischen Koordinatensystems mit x-, y- und z-Koordinaten wählen. Die drei Spannungsvektoren auf den drei Schnittflächen entsprechen dann den Zeilen der folgenden Matrix mit den Spannungen als ihren Komponenten:

S={\begin{bmatrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\end{bmatrix}}

Bezüglich der Standardbasis entspricht sie dem Spannungstensor. Die Bedeutung der Indizes zeigt die Skizze eines herausgeschnittenen Volumenelements. Im Doppelindex gibt der erste Index die Richtung an, in die der Normalenvektor der Schnittfläche zeigt, und der zweite Index, in welcher Richtung die Spannung wirkt. Der Spannungstensor ergibt, multipliziert mit dem Normaleneinheitsvektor ${\hat {n}}$ einer Schnittfläche, den Spannungsvektor auf dieser Fläche (Kraftvektor pro Flächeneinheit):

{\vec {T}}^{({\hat {n}})}=S^{\top }{\vec {\hat {n}}}.

Bei den „aktuellen“ oder „wahren“ Cauchy’schen Spannungen ist die Matrix symmetrisch, so dass also beispielsweise τ_xy = τ_yx ist und daher in obiger Formel die Transposition ( · )^T weggelassen werden kann.

Wenn die Spannungsmatrix in einem anderen Koordinatensystem aufgestellt wird, dann ändern sich ihre Komponenten in charakteristischer Weise, so wie sich auch die Komponenten eines geometrischen Vektors beim Wechsel des Basissystems ändern. Der Betrag des Vektors ändert sich dabei aber nicht und genauso gibt es beim Spannungstensor sogenannte Invarianten, die sich bei einem Basiswechsel nicht ändern. Beim Spannungstensor sind vor allem folgende Invarianten bedeutsam:

der Druck, der der negative Mittelwert der Diagonalelemente ist und der proportional zur Spur der Spannungsmatrix ist,
die von Mises Vergleichsspannung, die eine Invariante des Spannungsdeviators ist,
die Hauptspannungen und
die maximalen Schubspannungen, siehe unten.

Schub-, Druck- und Zugspannung

Die Diagonalelemente σ_xx,σ_yy,σ_zz in der Spannungsmatrix stellen die Normalspannungen dar, also die Spannungen, die senkrecht zur Koordinatenfläche wirken. Anders gesagt: Normalen- und Wirkrichtung stimmen überein.

Normalspannungen werden je nach Vorzeichen Zugspannung (positives Vorzeichen) oder Druckspannung (negatives Vorzeichen) genannt. Druckspannung wird gelegentlich auch als Flächenpressung bezeichnet.

Im Gegensatz zur Druckspannung ist Druck ausschließlich isotrop. Das heißt, Druck ist kein Vektor, sondern der negative hydrostatische Anteil des Spannungstensors. Er wirkt in allen Richtungen zugleich und ist daher der negative Mittelwert der Normalspannungen in den drei Raumrichtungen ( $p=-(\sigma _{xx}+\sigma _{yy}+\sigma _{zz})/3$ ). Er ist bei hydrostatischem Druck positiv und bei hydrostatischem Zug negativ. (Letzterer kann nur in Festkörpern vorkommen, da es sich beim scheinbaren hydrostatischen Zug in einem vakuumierten Gefäß tatsächlich um Druck handelt, der von außen auf das Gefäß wirkt.)

Die nichtdiagonalen Elemente τ_ij werden als Schubspannungen bezeichnet. Sie wirken tangential zur Fläche, stellen also eine Scherbelastung dar.

Hauptspannung und Hauptspannungsrichtung

Ebener Spannungszustand

Hauptspannungen im ebenen Spannungszustand

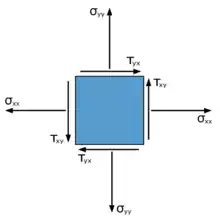
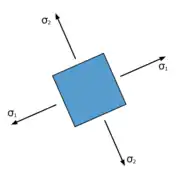
Zu jedem Spannungszustand im Gleichgewicht lassen sich durch Hauptachsentransformation drei paarweise senkrechte Richtungen finden, in denen bei Zug und Druck keine Schubspannungen auftreten, siehe Bilder. In diesen Hauptspannungsrichtungen wirken die Hauptspannungen σ_1,2,3.

Die Hauptspannungen lassen sich durch das Lösen der Gleichung $\det(S-\sigma E)=0$ errechnen, wobei E die 3×3-Einheitsmatrix ist. Ausmultiplizieren der Determinante det führt auf eine Gleichung dritten Grades in σ, deren Lösungen die gesuchten Hauptspannungen darstellen. Sie sind die Eigenwerte der Spannungsmatrix S und sämtlich reell, weil die Matrix symmetrisch ist. Ein hydrostatischer Spannungszustand liegt vor, wenn die drei Hauptspannungen gleich sind. (Hier treten keine Schubspannungen auf.)

Die jeweilige Hauptspannungsrichtung ergibt sich aus der Gleichung $S{\vec {e}}=\sigma {\vec {e}}$ , wobei für $\sigma$ die errechnete Hauptspannung eingesetzt wird. Die Lösungen ${\vec {e}}_{1,2,3}$ sind Eigenvektoren der Spannungsmatrix S und geben die Richtung der Hauptspannungen an. In normierter Form bilden sie eine Orthonormalbasis des dreidimensionalen Raumes oder lassen sich entsprechend orthogonalisieren. In den Hauptspannungsrichtungen sind die Schnittspannungen betraglich extremal. Die Kurvenschar der Hauptspannungslinien nennt man Spannungstrajektorien.

Der Mohrsche Spannungskreis gibt einen graphischen Eindruck der Abhängigkeit der Normal- und Schubspannung von der Normalenrichtung in der von zwei Hauptspannungsrichtungen aufgespannten Ebene. Die Hauptschubspannungen

\tau _{1}={\frac {|\sigma _{2}-\sigma _{3}|}{2}},\quad \tau _{2}={\frac {|\sigma _{3}-\sigma _{1}|}{2}},\quad \tau _{3}={\frac {|\sigma _{1}-\sigma _{2}|}{2}}

sind kritische Schubspannungen und treten in Schnittebenen auf, die normal zu den Winkelhalbierenden zwischen den Hauptspannungsrichtungen sind. Sei σ₁ die größte und σ₃ die kleinste Hauptspannung. Dann ist die maximale Schubspannung

\tau _{\mathrm {max} }={\frac {|\sigma _{1}-\sigma _{3}|}{2}}.

Werde die xy-Ebene wie in den Bildern durch die 1- und 2-Hauptspannungsrichtungen aufgespannt. Dann lauten die Hauptspannungen und die Hauptschubspannung bei einem gegebenen Spannungszustand in dieser Ebene

{\begin{aligned}\sigma _{1,2}=&{\frac {\sigma _{xx}+\sigma _{yy}}{2}}\pm \tau _{3}\\\tau _{3}=&{\sqrt {\left({\frac {\sigma _{xx}-\sigma _{yy}}{2}}\right)^{2}+\tau _{xy}^{2}}}\end{aligned}}

Die Winkel zur x-Achse, in denen die Hauptspannungen auftreten, ist

\tan(2\cdot \varphi _{1,2})={\frac {2\tau _{xy}}{\sigma _{xx}-\sigma _{yy}}}.

Zusammenhänge in der Festigkeitslehre

Ein realer, Spannungen ausgesetzter Körper deformiert sich.

Den Zusammenhang zur Deformation stellt für elastische Verformungen das Hooke’sche Gesetz her. Wichtigste Materialkonstanten sind dabei Elastizitätsmodul, Schubmodul und Querkontraktionszahl.

Die plastische Deformation wird durch die Fließbedingung, das Fließgesetz und das Verfestigungsgesetz beschrieben. Im Hauptspannungsraum, in dem die Hauptspannungen auf den Koordinatenachsen aufgetragen werden, stellt ein Spannungszustand einen Punkt oder Vektor dar, den man in zwei Komponenten zerlegen kann:

Die (deviatorische) Komponente quer zur Raumdiagonalen im Hauptspannungsraum, also quer zum hydrostatischen Spannungsanteil, ist ein Maß dafür, wie groß die Schubspannungen je nach Schnittrichtung maximal werden können. Allein dieser Anteil ist bei der Berechnung von Stahlkonstruktionen relevant. Er entspricht der von Mises Vergleichsspannung nach der Gestaltänderungshypothese und ist eine Funktion des Betrages des Spannungsdeviators. Wenn diese Vergleichsspannung die Fließspannung des Stahls überschreitet, verformt sich der Stahl plastisch.
Die Komponente in Richtung der Raumdiagonalen beschreibt den Druck; dieser Anteil ist bei der Berechnung von Stahlkonstruktionen irrelevant, da er in keinerlei Schnittrichtung zu Schubspannungen führt, und insofern auch zu keiner plastischen Verformung.

Ein Festkörper kann auch Eigenspannungen besitzen, die ohne von außen an den Körper angreifende Kräfte auftreten.

Im Allgemeinen hängt das Deformationsverhalten eines Körpers von seiner Form und den Eigenschaften der Materialien ab, aus denen er besteht. Die Materialeigenschaften werden in einem Materialmodell mathematisch durch einen Zusammenhang zwischen Spannungs- und Verzerrungstensor sowie ihren Raten und zeitlichen Verläufen beschrieben. Mit den Materialmodellen können bei gegebenem Körper, seinen Lagerungen und Belastungen die Spannungen in ihm berechnet werden. Die Rheologie, Materialwissenschaft und Werkstofftechnik sowie Materialtheorie beschäftigen sich mit dem Fließ- und Deformationsverhalten von Materialien und machen es möglich, die Spannungen rechnerisch zu ermitteln.

Zusammenhänge in der Strömungsmechanik

Den Zusammenhang zur Verformungsgeschwindigkeit in linear-viskosen Flüssigkeiten und Gasen (Fluide) stellt Newtons Zähigkeitsansatz her. Wichtigste Materialkonstante ist darin die dynamische Viskosität. Ursache der Viskosität ist die Reibung und der Impulstransport zwischen den Fluidelementen.

Bei laminarer Strömung und genügend großer Reynolds-Zahl kann im Großteil eines Strömungsfelds die Viskosität des strömenden Fluids vernachlässigt werden. Hier ist die dominierende Spannung im Fluid der Druck. Der Totaldruck teilt sich auf in den dynamischen und den statischen Druck. Der dynamische Druck speist sich aus der kinetischen Energie der Fluidelemente. Der statische Druck ist jener Druck, den ein mit der Strömung mitbewegtes Fluidelement verspürt. Er wird in Gasen mit Zustandsgleichungen und im Fall des idealen Gases durch Gasgesetze beschrieben.

Keinesfalls zu vernachlässigen ist der Einfluss der Viskosität in der Grenzschicht an umströmten Wänden. Die Dicke dieser Grenzschicht ist bei anliegender Strömung zwar sehr klein, in ihr bildet sich aber über die Wandschubspannung der Schubspannungswiderstand des umströmten Körpers, der mit dem Druckwiderstand zusammen den gesamten Strömungswiderstand eines Körpers ausmacht.

Bei Grenzschichtablösungen kann die Wandschubspannung verschwinden oder gar entgegen der Außenströmung wirken. Solche Ablösungen können dramatische Auswirkungen haben, wenn sie an Tragflügeln oder in Strahltriebwerken auftreten.

Literatur

H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 3. Auflage. Springer-Vieweg, 2014, ISBN 978-3-642-40980-6.
Heinz Parkus: Mechanik der festen Körper. 2. Auflage, 6. Nachdruck. Springer, Wien/ New York 2009, ISBN 978-3-211-80777-4.
Christian Spura: Technische Mechanik 2. Elastostatik. 1. Auflage. Springer, Wiesbaden 2019, ISBN 978-3-658-19979-1.

Einzelnachweise

H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 2014, S. 32.
Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Berlin: Ernst & Sohn, S. 396, ISBN 978-3-433-03229-9
Herbert Mang, Günter Hofstetter: Festigkeitslehre. 3. Auflage. Springer Verlag, Wien/ New York 2008, ISBN 978-3-211-72453-8, 6.4 „Normalspannungen“, S. 156 (springer.com).
H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 2014, S. 63ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 2014, S. 32.

[2] Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Berlin: Ernst & Sohn, S. 396, ISBN 978-3-433-03229-9

[mang2008festigkeitslehre-3] Herbert Mang, Günter Hofstetter: Festigkeitslehre. 3. Auflage. Springer Verlag, Wien/ New York 2008, ISBN 978-3-211-72453-8, 6.4 „Normalspannungen“, S. 156 (springer.com).

[4] H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 2014, S. 63ff.