Materialmodell

Ein Materialmodell, Material- oder Stoffgesetz, ist eine Quantifizierung von physikalischen Materialeigenschaften. Materialeigenschaften konstatieren die Fähigkeit eines Materials auf physikalische Einflüsse (wie Kräfte, Wärmezufuhren oder Ströme) zu reagieren. Materialmodelle sind unabhängig von der Form eines Körpers und sind meist experimentell motiviert. Ziel eines Materialmodells ist, vorhersagen zu können, wie und in welchem Maß das Material auf äußere Einflüsse reagiert. Als Modelle bilden sie für den Modellersteller relevante Zusammenhänge mathematisch ab, sind also mathematische Modelle, die einen Urheber, den Modellersteller, besitzen. Auch wenn sie oftmals als Materialgesetze bezeichnet werden, haben sie nicht die allgemeine Gültigkeit physikalischer Gesetze, denn für dasselbe Material können verschiedene Modelle von verschiedenen Modellerstellern vorliegen, die sich im Anwendungsgebiet, den betrachteten Abhängigkeiten, dem Berechnungsaufwand, der Genauigkeit und ihrem Gültigkeitsbereich unterscheiden.

Die Reaktionen eines Materials nennt man Materialgrößen und die Einflussgrößen Konstitutivvariable. Die Verknüpfung der Konstitutivvariablen und Materialgrößen erfolgt in Gleichungen, die Material- oder Konstitutivgleichungen genannt werden. Des Weiteren können auch Ungleichungen auftreten, welche die verschiedene Verhaltensmodi (wie plastisches Fließen, Phasenübergänge) des Materials voneinander trennen. Der denkbar einfachste Zusammenhang zwischen Materialgröße und Konstitutivvariable ist die Proportionalität: Die Materialgröße ist gleich einer Konstitutivvariable multipliziert mit einer Konstanten. Ein solcher Zusammenhang hat oftmals definitorischen Charakter für eine Stoffeigenschaft, wie die Beispiele Spezifische Wärmekapazität, Permittivität, Permeabilität (Magnetismus) auf der Seite Materialkonstante zeigen. Materialeigenschaften und daher auch die Materialkonstanten sind immer von der Temperatur abhängig, was man mit Temperaturkoeffizienten berücksichtigen kann. Werden im betrachteten Berechnungsfall weitere oder komplexere Abhängigkeiten als relevant erachtet, tritt der Modellersteller auf den Plan, der dann ein für den betrachteten Fall geeignetes Modell erstellt (sofern es das noch nicht gibt). So ist die Entwicklung von der ersten Definition einer Eigenschaft und Quantifizierung mit einer Materialkonstanten über die Berücksichtigung einer Temperaturabhängigkeit hin zu komplexen Modellen nachgezeichnet. Ursachen der Komplexität können Nichtlinearitäten, Mehrachsigkeit oder Abhängigkeit von mehreren Konstitutivvariablen sein.

Die Kontinuumsmechanik hat einen eigenen Wissensbereich, die Materialtheorie, die sich mit der Klassifizierung von Materialien und Materialeigenschaften und der Erstellung von Materialmodellen beschäftigt. Die Materialwissenschaft und Werkstofftechnik entwickelt Materialmodelle aus dem Bedürfnis heraus, die von ihr entwickelten Werkstoffe möglichst genau zu charakterisieren.

Gültigkeitsbereich

Materialmodelle haben eine eingeschränkte Gültigkeit, weil sie vom Modellersteller ausgeklammerte Einflüsse nicht berücksichtigen. Bei der Anwendung der Modelle ist darauf zu achten, ob die dem Modell zu Grunde liegenden Annahmen zutreffen wie zum Beispiel:

Umgebungsbedingungen wie Temperatur oder Druck
Zeitspannen über die das Materialverhalten beobachtet werden soll (Langzeit- oder Kurzzeitverhalten).
Änderungsraten der Konstitutivvariablen. Man unterscheidet statische, quasi statische, moderate Raten oder Hochgeschwindigkeitsbereiche.
Größenskala der Materialproben. Man unterscheidet Makro-, Meso- oder Mikroebene der Betrachtung.
Chemischer Zustand. Materialien können durch Korrosion ihre Eigenschaften verändern.

Physikalischer Rahmen

Materialien unterliegen einerseits den physikalischen Gesetzen wie Massen-, Impuls- und Energieerhaltung oder den Maxwellschen Gleichungen. Andererseits folgt eine Materialprobe geometrischen Bindungen, die das Fachgebiet der Kinematik sind und die die möglichen Bewegungen und daraus resultierende Verformungen und Dehnungen beschreibt. Materialmodelle, die einen quantitativen Zusammenhang zwischen den Variablen in diesen physikalischen und kinematischen Gleichungen angeben, sind dazu geeignet, die Reaktionen eines den Naturgesetzen folgenden Körpers auf äußere Einflüsse zu berechnen.

Der zweite Hauptsatz der Thermodynamik hat einen Sonderstatus: Bei der Aufstellung von Materialmodellen muss darauf geachtet werden, dass bei allen möglichen zeitlichen Verläufen der Konstitutivvariablen die Entropieproduktion des Materials nicht negativ ist.

Einfache Materialien

Manche Materialeigenschaften sind so komplex, dass sie mehr exemplarisch anhand der Reaktion von Prüfkörpern dargestellt werden. Beispiele hierfür sind die Schlagzähigkeit, Kerbschlagzähigkeit oder Bauteil-Wöhlerlinien. Es handelt sich hier also eher um Bauteileigenschaften, weil die Trennung von Materialeigenschaft und Probeneigenschaft (Form, Größe oder Oberflächenbeschaffenheit des Prüfkörpers) nicht zuverlässig oder nicht mit vertretbarem Aufwand gelingt. Bei den meisten Materialeigenschaften hat sich jedoch die Vorstellung bewährt, dass jeder beliebige Teil einer Materialprobe die gleichen Eigenschaften wie die Probe selbst hat. Für die Bestimmung der Materialantwort an einem Punkt der Probe braucht man dann nur eine (infinitesimal) kleine Umgebung des Punktes in Betracht zu ziehen. Das Material reagiert lokal auf lokale Einflüsse. Ferner lehrt die Erfahrung, dass die Materialantwort vollständig von vergangenen oder gegenwärtigen nicht aber von zukünftigen Einflüssen abhängt, dass Materialien also deterministisch sind. Das Prinzip von der materiellen Objektivität besagt, dass ein beliebig translatorisch oder rotatorisch bewegter Beobachter die gleiche Materialantwort misst wie ein relativ zur Probe ruhender Experimentator. Materialien die lokal, deterministisch und objektiv sind nennt man einfach und nur solche sind der Gegenstand der klassischen Materialtheorie.

Materialgleichungen

Objektive Größen

Für Materialgrößen und Konstitutivvariable können nur objektive Größen verwendet werden, d. h. solche die ein beliebig translatorisch oder rotatorisch bewegter Beobachter in gleicher Weise wahrnimmt wie ein relativ zur Probe ruhender Experimentator. Masse, Dichte, Temperatur, Wärme, spezifische innere Energie und Entropie sind skalare objektive Größen. Objektive gerichtete Größen, Vektoren, sind z. B. Kräfte, Spannungs-, Wärmefluss- und Entropieflussvektoren. Die Geschwindigkeit eines Partikels ist aber z. B. keine objektive Größe, weil sie von unterschiedlich bewegten Beobachtern unterschiedlich beurteilt wird. Des Weiteren treten in manchen Naturgesetzen tensorielle Größen auf, deren Objektivität im Einzelfall zu prüfen ist. Als wichtiges Beispiel sei hier nur der Cauchy’sche Spannungstensor erwähnt, der eine objektive Größe ist.

Arten von Materialgleichungen

Gleichungen, die ein Material beschreiben, können in drei Klassen eingeteilt werden:

Solche die die materielle Symmetrie oder Richtungsabhängigkeit angeben. Bei einer solchen sind die Eigenschaften des Materials in der einen Richtung anders als in der anderen. Ein bekanntes Beispiel dafür ist Holz, das sich in Faserrichtung anders verhält als quer dazu.
Materielle Zwangsbedingungen verbieten einem Material bestimmte Veränderungen. Bekanntestes Beispiel hierfür ist die Inkompressibilität, bei der das Volumen einer Materialprobe unveränderlich ist.
Konstitutive Gleichungen, die den funktionalen Zusammenhang zwischen Materialgrößen und den Konstitutivvariablen formulieren.

Während die Mitglieder der ersten beiden Klassen algebraischer Natur sind, können bei den konstitutiven Gleichungen auch andere Formen auftreten:

Differentialgleichungen,
Integralgleichungen,
algebraische Gleichungen und
Ungleichungen,

siehe das Beispiel unten.

Konservative Materialien

Konservative Materialien besitzen eine besondere Form von konstitutiven Gleichungen bei denen die Materialgröße sich aus der Ableitung eines Skalarpotentials nach der Konstitutivvariablen ergibt. Ein Beispiel hierfür ist das Hookesche Gesetz wo das Potential die Formänderungsenergie ist. Hier hat man die besonderen Eigenschaften:

Wegunabhängigkeit: Die Materialgröße hat bei gegebenen Wert der Konstitutivvariablen immer denselben Wert, egal auf welchem Weg der Endzustand erreicht wurde.
Konservativität: Ist das Potential eine Energie, so wird entlang eines geschlossenen Weges keine Arbeit verrichtet oder Energie verbraucht. Aufgewendete Arbeiten werden vom System bis zur Rückkehr zum Ausgangspunkt vollständig zurückgegeben.

Materialparameter

Für die Quantifizierung des Materialverhaltens enthalten die konstitutiven Gleichungen Materialparameter oder – wie sie auch genannt werden – Materialkonstanten, die gestatten das Modell an gemessene Werte anzupassen. Es ist allgemein üblich das Modell so zu gestalten, dass die Parameter bei realen Materialien positive Werte haben. Sollten bei der Anpassung negative Werte auftreten, ist in der Regel Vorsicht geboten.

Mechanische Feststoffmodelle

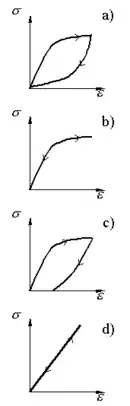
Auswahl von einachsigen Stoffgesetzen:
a: viscoelastisch.
b: ideal elastisch.
c: plastisch.
d: ideal linear elastisch

Die nachfolgende Aufstellung zeigt Repräsentanten der vier Materialmodelle der klassischen Kontinuumsmechanik für Feststoffe.

Ist der Spannungs-Dehnungs-Verlauf bei Belastung- und Entlastung identisch, so ist das Stoffgesetz elastisch oder ideal elastisch (b oder d im Bild) und nicht viskos, d. h. geschwindigkeitsunabhängig. Ideal elastische Stoffgesetze müssen nicht unbedingt linear, sondern können auch nichtlinear sein (b im Bild). Ist ein Stoffgesetz linear und ideal elastisch (d im Bild), so spricht man von einem linear ideal elastischen Gesetz. Da dieser Ausdruck sehr lang ist, spricht man abgekürzt von einem linearen Elastizitätsgesetz oder einfach nur von einem Elastizitätsgesetz, z. B. beim Hookeschen Gesetz.

Kommt der Spannungs-Dehnungs-Verlauf bei der Entlastung wieder am Startpunkt an, unterscheidet sich aber der Pfad bei Entlastung von dem bei Belastung (a im Bild), so ist das Stoffgesetz viscoelastisch und man sieht eine Hysterese. Bei sehr langsamen Spannungs-Dehnungs-Verläufen verschwindet die Hysterese und man sieht einen Verlauf wie im Bild b. Gummiartige Stoffe zeigen ein solches Verhalten.

Sind Start- und Endpunkt nicht gleich, so spricht man von einem plastischen Stoffgesetz (c im Bild). Dies gilt für Stoffe, die während der Belastung fließen, siehe auch das Beispiel unten. Hier beobachtet man eine von der Dehnungsgeschwindigkeit unabhängige Hysterese.

Sind Start- und Endpunkt nicht gleich und man beobachtet eine von der Dehnungsgeschwindigkeit abhängige Hysterese, die aber auch bei sehr langsamen Spannungs-Dehnungs-Verläufen nicht verschwindet, liegt Viscoplastizität vor. Die Hysteresekurve bei sehr langsamen Spannungs-Dehnungs-Verläufen nennt man hier Gleichgewichtshysterese.

Die vier genannten Materialklassen sind also von der Dehnungsgeschwindigkeit abhängig oder unabhängig und zeigen eine Gleichgewichtshysterese oder nicht. Das Kriechen ist eine Eigenschaft viskoser Stoffe.

Besteht ein linearer Zusammenhang zwischen der Spannung und der Dehnung, so spricht man von einem linearen Stoffgesetz (d im Bild). Es muss auch bezüglich seiner Temperaturausdehnung linear sein. Gesetze, die keinen linearen Zusammenhang zeigen, nennt man nichtlineare Stoffgesetze.

Beispiel

Dehnungsgeschichte beim Zugversuch

Spannungsverlauf

Spannungsdehnungsdiagramm eines ideal plastischen Materials

Als Beispiel soll die ideale Plastizität dienen, deren Materialgleichungen sowohl algebraische als auch Differentialgleichungen und eine Fallunterscheidung beinhalten. Bei der idealen Plastizität tritt beim plastischen Fließen keine Verfestigung auf, d. h. die Spannungs-Dehnungs-Kurve hat beim Fließen einen horizontalen Verlauf. Knete ist in etwa ideal plastisch. In der Praxis findet dieses Modell Anwendung, wenn nur die Fließgrenze bekannt ist und man bei der Berechnung der Steifigkeit eines Bauteils diese auf keinen Fall überschätzen will.

Im wichtigen Sonderfall des einachsigen Zuges/Druckes kann man sich auf skalare Größen beschränken und die Materialgleichungen sehr vereinfachen. Der Weg dorthin wird wie in einem mehrachsigen Plastizitätsmodell mit mehreren Konstitutivvariablen beschritten. Die Konstitutivvariable ist die Gesamtdehnung $\varepsilon$ und die Materialgröße ist die Spannung $\sigma$ . Im Zugbereich ist die Spannung positiv, im Druckbereich negativ. Das Material besitzt einen elastischen Bereich, in dem das Material elastisch reagiert und einen plastischen Bereich, wo plastisches Fließen stattfindet. Das Fließen wird mit der plastischen Dehnung $\varepsilon _{p}$ dargestellt, die eine innere Variable des Modells ist. Die plastische Dehnung kann also nicht direkt von außen beeinflusst oder vorgegeben werden. Die Differenz zwischen der Gesamtdehnung und der plastischen Dehnung ist die elastische Dehnung. Die Gesamtdehnung wird also in einen elastischen und einen plastischen Anteil zerlegt:

\varepsilon =\varepsilon _{e}+\varepsilon _{p}

worin $\varepsilon _{e}$ der elastische Anteil ist. Die Spannung hängt über ein Elastizitätsgesetz von der elastischen Dehnung ab:

\sigma =E\;\varepsilon _{e}

worin der Materialparameter $E$ Elastizitätsmodul heißt. Die plastische Dehnung entwickelt sich nur wenn die Spannung die Fließgrenze $k$ erreicht, die ein weiterer Materialparameter ist. Die Fließfunktion $f$ gibt die Fallunterscheidung zwischen elastischem und plastischem Bereich an:

f=\sigma ^{2}-{k}^{2}\leq 0

.

Im elastischen Bereich ist $f<0$ . Bei plastischem Fließen ist $f=0$ und daher ${|}\sigma {|}=k=\mathrm {const.}$ , was das besondere Merkmal der idealen Plastizität ist. Allerdings kann ${|}\sigma {|}=k$ auch bei konstanter Dehnung gelten, weswegen Fließen erst eintritt, wenn $\sigma {\dot {\varepsilon }}>0$ ist. Die Fließbedingung lautet also

f=0

und

\sigma {\dot {\varepsilon }}>0

.

Eine assoziative Fließregel bestimmt im Fall plastischen Fließens die Evolution der plastischen Dehnung:

{\dot {\varepsilon }}_{p}=\lambda {\frac {\partial f}{\partial \sigma }}=2\lambda \sigma

.

Darin ist $\lambda$ der plastische Multiplikator, der sich aus der Konsistenzbedingung ${\dot {f}}=0$ ableitet:

{\dot {f}}=2\sigma {\dot {\sigma }}=2\sigma E\,{\dot {\varepsilon }}_{e}=2\sigma E\,\left({\dot {\varepsilon }}-{\dot {\varepsilon }}_{p}\right)=2E\,\sigma \left({\dot {\varepsilon }}-2\lambda \sigma \right)=0\rightarrow \lambda ={\frac {\dot {\varepsilon }}{2\sigma }}={\frac {\sigma {\dot {\varepsilon }}}{2\sigma ^{2}}}>0

bei plastischem Fließen. Für die Evolution der plastischen Dehnung bedeutet das:

{\dot {\varepsilon }}_{p}=2\lambda \sigma =2{\frac {\dot {\varepsilon }}{2\sigma }}\sigma ={\dot {\varepsilon }}\rightarrow {\dot {\varepsilon }}_{e}=0\rightarrow {\dot {\sigma }}=0

.

Umgekehrt ist im elastischen Bereich ${\dot {\varepsilon }}_{p}=0$ , also ${\dot {\sigma }}=E{\dot {\varepsilon }}_{e}=E{\dot {\varepsilon }}$ .

Die Materialgleichungen der idealen Plastizität können also im einachsigen Fall wie folgt zusammengefasst werden:

Fließfunktion	$f=\sigma ^{2}-{k}^{2}\leq 0$
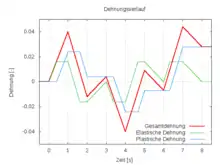
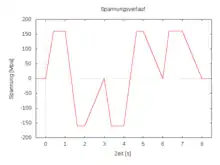
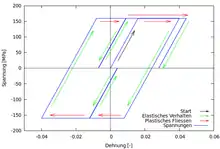
Spannungs-Dehnungs-Beziehung	${\dot {\sigma }}={\begin{cases}0&{\text{falls}}\quad f=0\;{\text{und}}\;\sigma {\dot {\varepsilon }}>0\\E{\dot {\varepsilon }}&{\text{sonst}}\end{cases}}$

In den Bildern rechts sind Diagramme eines simulierten dehnungsgesteuerten Zugversuchs angegeben. Das obere Bild zeigt den Verlauf der Dehnungen, das mittlere den Verlauf der Spannung über die Zeit und das untere Bild zeigt das Spannungs-Dehnungs-Diagramm dieses ideal plastischen Materials. Als Materialparameter wurden verwendet:

Parameter	$E$	$k$
Wert	10000	160
Einheit	MPa	MPa

Am Ende des Versuchs, nach acht Sekunden, wurde die Probe nach einer Gesamtdehnung von 0,045 entlastet, so dass die Spannung verschwindet, also $\sigma =0$ und daher auch $\varepsilon _{e}=0$ gilt. Am Ende beobachtet man aber verbleibende Dehnungen, die wegen $\varepsilon _{e}=0$ den plastischen Dehnungen entsprechen. Ihre Größe ist

\varepsilon =0{,}045-{\frac {k}{E}}=0{,}029=\varepsilon _{p}

.

Ein realer Körper aus diesem Material würde also am Ende des Versuchs nicht in seinen Ausgangszustand zurückkehren, was das Merkmal der Plastizität ist.

Literatur

H. Altenbach: Kontinuumsmechanik. Springer 2012, ISBN 978-3-642-24118-5.
Ralf Greve: Kontinuumsmechanik. Springer, 2003, ISBN 3-540-00760-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.