Rotationsachse
Eine Rotationsachse oder Drehachse ist eine Gerade, die eine Rotation oder Drehung beschreibt. Drehachsen spielen in verschiedenen Bereichen der Mathematik, der Technik und der Naturwissenschaften eine wichtige Rolle, sind aber jeweils speziell definiert. Je nach der Definition kann es sich um eine fiktive oder eine physikalisch reale Drehung handeln, in beliebigen oder fest definierten Winkeln.
Mathematik
Rotationskörper
Als Rotationsachse bezeichnet man bei einem Rotationskörper diejenige Gerade, um die man diesen in beliebigem Winkel drehen kann, ohne dass sich die Ansicht des Körpers verändert. In diesem Fall ist die Rotationsachse zugleich auch eine Symmetrieachse des Körpers. Die einzelnen Punkte des Körpers bewegen sich bei einer Rotation auf Kreisen in Ebenen senkrecht zur Rotationsachse. Der Begriff „Rotationskörper“ besagt, dass man sich dessen Entstehung durch Rotation einer durch eine Kurve begrenzten Ebene um die Rotationsachse denken kann. Bekannte Rotationskörper sind Zylinder, Kegel und Rotationsellipsoid.
Symmetrieachsen
Wenn die Ansicht eines Körpers nur in bestimmten Drehstellungen gleich ist, spricht man von einer Zähligkeit der Symmetrie bzw. der Drehachsen. Man unterscheidet zweizählige (Digyren), dreizählige (Trigyren), vierzählige (Tetragyren), fünfzählige (Pentagyren), sechszählige (Hexagyren) und vielzählige Symmetrie- bzw. Drehachsen.
Die Anzahl und Zähligkeit der Drehachsen bestimmen die Form des Körpers. So besitzt ein Würfel nicht nur – wie jeder Quader – drei zweizählige Drehachsen, sondern darüber hinaus vier senkrecht aufeinanderstehende dreizählige Drehachsen.
Die Kombination von Drehung und Achsenspiegelung führt zum Symmetrieelement der Drehspiegelachsen, diejenige von Drehung und Inversion zu den Drehinversionsachsen.
Drehsinn
Zur eindeutigen Beschreibung der Drehung muss die Drehrichtung definiert werden; dazu wird der Drehachse eine bestimmte Drehrichtung zugeteilt. Wenn sich der Kreis, vom Beobachter aus gesehen, im Uhrzeigersinn dreht, weist sein Blick in dieselbe Richtung wie die Richtung der Drehachse.
Physik
Körper können um beliebig viele Achsen frei gedreht werden. Eine besondere Bedeutung hat die Drehung um die Hauptträgheitsachsen für das Rotationsverhalten des Körpers. Auch bei der Beschreibung rotierender Bezugssysteme ist die Drehachse heranzuziehen.
Eine Rotationsachse lässt sich anhand eines Rades veranschaulichen. Die Rotationsachse steht senkrecht auf der Radscheibe und dem kreisförmigen Radreifen. In abstrakter Betrachtungsweise kommt man ohne Scheibe und Reifen aus. Alle Punkte des Rades bewegen sich auf Kreisbahnen, die Ebenen aufspannen, auf denen die Drehachse senkrecht steht.
Technik
In der Technik wird der Begriff vorwiegend bei Drehungen um feste Rotationsachsen verwendet, z. B. bei Robotern. Bei freien Drehungen starrer Körpern im Raum wird der Begriff zwar auch gelegentlich benutzt, wird aber wegen der Mehrdeutigkeit bei Straßenfahrzeugen in der Normung (DIN ISO 8855 Fahrzeugdynamik und Fahrverhalten – Begriffe) nicht verwendet. Eindeutig ist die Angabe der Winkelgeschwindigkeit und der Bewegung des Bezugspunkts. Die Winkelgeschwindigkeit kann noch in Komponenten, z. B. um die Koordinatenachsen oder um die Hauptträgheitsachsen, angegeben werden.
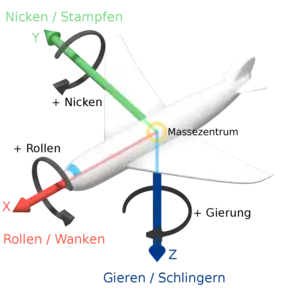
In der Fahrzeugtechnik setzt sich die Winkelgeschwindigkeit des fahrzeugfesten Bezugssystems aus den Elementardrehungen um die Koordinatenachsen zusammen. Diese sind:
- Längsachse: Rollachse (engl. roll axis) oder Wankachse (bei Landfahrzeugen): Rotation um die in Längsrichtung des Fahrzeugs verlaufende -Achse.
- Querachse: Nickachse (engl. pitch axis): Rotation um die -Achse des Fahrzeugs. Bei Straßenfahrzeugen nach links
- Hoch- oder Vertikalachse: Gierachse (engl. yaw axis): Rotation um die -Achse des Fahrzeugs. Bei Straßenfahrzeugen nach oben.
Die tatsächliche Rotationsachse geht im Fall einer ebenen Bewegung durch den Momentanpol. Bei einer stationären Kurvenfahrt eines PKW auf ebener Fahrbahn wäre das der Kurvenmittelpunkt. Bei einer räumlicher Bewegung eines starren Körpers ist die Rotationsachse gleich der Schraubachse.
Kristallographie

Obwohl die Bausteine eines Kristalls nahezu unbeweglich sind (abgesehen von den Schwingungen um ihre Ruhelage), sind die Drehachsen als Symmetrieelemente unabdingbar zur Beschreibung sowohl der makroskopisch sichtbaren Kristallformen als auch der inneren Anordnung der Kristallbausteine (Kristallstruktur) in der Kristallographie.
Bei einer – theoretisch räumlich unbegrenzten – Kristallstruktur treten nur Achszähligkeiten von 2, 3, 4 und 6 auf. Bei der Beschreibung von Punktgruppen bzw. Kristallklassen mit Hilfe der Hermann-Mauguin-Symbolik werden zweizählige Drehachsen beispielsweise mit „2“ und dreizählige Drehachsen mit „3“ bezeichnet. Zur Kennzeichnung der Raumgruppen wird die Drehung mit der Translation verknüpft, wodurch man kristallographische Schraubenachsen erhält.
Wegen der Achszähligkeiten hat ein Kristall niemals die Form eines Rotationskörpers. Die Hauptdrehachsen sind bei makroskopischen Kristallen meist sehr auffällig und bilden die Grundlage für die Klassifikation der Kristallsysteme. Bei mikrokristallinen Stoffen wird die Lage der Drehachsen mit Hilfe der Röntgenstrukturanalyse aufgeklärt.
Molekülphysik bzw. Chemie

Auch die Gestalt von Molekülen ist mit Symmetrieelementen beschreibbar. Diese geben an, durch welche Symmetrieoperationen das Molekül mit sich selbst zur Deckung gebracht werden kann. Da es sich bei Molekülen im Gegensatz zur Kristallstruktur um diskrete Objekte handelt, sind bei den Drehachsen prinzipiell alle Zähligkeiten möglich, z. B. eine fünfzählige Achse beim Ferrocen. Weiterhin gibt es die beliebige Zähligkeit in der Längsachse der Moleküle bei linearen Molekülen.
Im flüssigen Zustand, wo eine bedingte, und im gasförmigen Aggregatzustand eins Stoffes, wo eine freie Beweglichkeit der Moleküle vorliegt, können diese Drehachsen die Achsen realer Bewegungen sein.
Die Drehachsen werden in der Schoenflies-Symbolik mit bezeichnet, wobei „“ zyklisch bedeutet und der Index die Zähligkeit angibt. Lage, Anzahl und Zähligkeit der Drehachsen im Molekül beeinflussen in die Resultate der Schwingungs- und Rotationsspektroskopie.
Im Allgemeinen entspricht die Kristallsymmetrie eines Feststoffs nicht der Molekülsymmetrie seiner Bausteine. So besitzt das Wasser-Molekül eine zweizählige Drehachse, der Eiskristall jedoch eine sechszählige, was morphologisch in den hexagonalen Schneekristallen sichtbar wird.
Einzelnachweise
- Erwin Riedel und Christoph Janiak: Anorganische Chemie, 8. Auflage, 2011, Walter de Gruyter Verlag, S. 213, ISBN 978-3-11-022566-2.
