Chaosforschung

Die Chaosforschung oder Chaostheorie bezeichnet ein nicht klar umgrenztes Teilgebiet der nichtlinearen Dynamik bzw. der dynamischen Systeme, welches der mathematischen Physik oder angewandten Mathematik zugeordnet ist.

Im Wesentlichen beschäftigt sie sich mit Ordnungen in speziellen dynamischen Systemen, deren zeitliche Entwicklung unvorhersagbar erscheint, obwohl die zugrundeliegenden Gleichungen deterministisch sind. Dieses Verhalten wird als deterministisches Chaos bezeichnet und entsteht, wenn Systeme empfindlich von den Anfangsbedingungen abhängen: Kaum unterscheidbare Wiederholungen eines Experimentes können im Langzeitverhalten zu höchst unterschiedlichen Messergebnissen führen (die Chaostheorie besagt also nicht, dass identische Anfangsbedingungen zu verschiedenen Ergebnissen führen würden). Chaotische dynamische Systeme sind nichtlinear.

Als einführendes Beispiel wird oft auf das magnetische Pendel oder das Doppelpendel verwiesen. Andere Beispiele sind der Schmetterlingseffekt[1] beim Wetter, Turbulenzen, Wirtschaftskreisläufe, bestimmte Musterbildungsprozesse, wie beispielsweise Erosion, die Entstehung eines Verkehrsstaus, neuronale Netze sowie Laser[2].

Die Chaosforschung basiert unter anderem auf Arbeiten von Henri Poincaré, Edward N. Lorenz, Benoît Mandelbrot und Mitchell Feigenbaum. Die hier dargestellten Phänomene entsprechen dem Minimalkonsens darüber, was thematisch zur Chaosforschung zählt.

Grundlagen

Klassifikation des Verhaltens eines magnetischen Pendels über drei Magneten; jede Stelle entspricht einem Startpunkt für die Pendelbewegung. Die Farbe charakterisiert den Magneten, an dem das Pendel zum Stillstand kommt. Je heller die Farbe, umso früher ist das der Fall. Die drei hellsten Stellen markieren daher die Positionen der Magnete.

Die Chaostheorie beschreibt das zeitliche Verhalten von Systemen mit deterministisch chaotischer Dynamik. Versucht man Experimente identisch zu wiederholen, so ist das in der Praxis nicht möglich, da auf Grund unvermeidbarer Messungenauigkeiten – und durch Rauschen – die Ausgangssituation nicht identisch wiederhergestellt werden kann. Falls ein System deterministisch chaotisch ist, so kann das System nach hinreichend langer Zeit trotz experimentell fast identischer (bzw. bestmöglich identischer) Ausgangssituationen zu deutlich anderen Endzuständen bzw. Messergebnissen führen.

Dies wird als „sensitive Abhängigkeit von den Anfangsbedingungen“ bezeichnet. Am Computer können solche Systeme simuliert werden und diese Simulationen prinzipiell identisch oder mit kleinen Abweichungen wiederholt werden. Die Sensitivität der Anfangsbedingung tritt hier in der Form auf, dass, wenn man z. B. die Genauigkeit der Startbedingung geringfügig ändert, das Ergebnis der Simulation grundlegend modifiziert wird. Dies liegt daran, dass anfangs beliebig dicht liegende Trajektorien am Ende der Simulation diese Eigenschaft nicht mehr besitzen. (Mathematisch: Die Stetigkeit der Abbildung ist zwar für kleine Zeiten gegeben, im Limes großer Zeiten aber nicht mehr.)

In der nebenstehenden Abbildung sind die durch Punkte in der Ebene charakterisierten Anfangsbedingungen je nach Endzustand unterschiedlich gefärbt. Es gibt einerseits Bereiche (hier: im Außengebiet), die fraktale Strukturen bilden, obwohl die zugehörigen Anfangsbedingungen mit verschiedenen Endzuständen beliebig dicht liegen und andererseits deterministische Bereiche (hier: mehr im Innern), also Gebiete in denen benachbarte Anfangsbedingungen alle den gleichen Endzustand haben.

Anders als der Begriff Chaos in der Umgangssprache verwendet wird, befasst sich die Chaostheorie nicht mit Systemen, die dem Zufall unterliegen (also stochastischen Systemen), sondern mit dynamischen Systemen, die mathematisch beschreibbar sind und sich prinzipiell deterministisch verhalten. Des Weiteren ist die Chaostheorie abzugrenzen von der Theorie komplexer Systeme, da auch sehr einfache Systeme chaotisches Verhalten zeigen können.

Definition

Ein dynamisches System $(T,X,f)$ heißt chaotisch, wenn eine $f$ -invariante Menge $Y\subseteq X$ existiert, d. h. für jedes $t\in T$ und jedes $y\in Y$ ist $f(t,y)\in Y$ , für die gilt:

$f$ besitzt sensitive Abhängigkeit von den Anfangsbedingungen auf $Y$ .
$f$ ist topologisch transitiv auf $Y$ :
Zu allen offenen Mengen $U,V\subseteq X$ mit $U\cap Y\neq \emptyset \neq V\cap Y$ existiert ein $t>0$ , sodass $f(t,U)\cap V\neq \emptyset$ .[3]
Die periodischen Orbits von $f$ liegen dicht in $Y$ .

Grenzen der Vorhersagbarkeit

Liegt chaotisches Verhalten vor, dann führen selbst geringste Änderungen der Anfangswerte nach einer endlichen Zeitspanne, die vom betrachteten System abhängt, zu einem völlig anderen Verhalten (sensitive Abhängigkeit von den Anfangsbedingungen). Es zeigt sich also ein nichtvorhersagbares Verhalten, das sich zeitlich scheinbar irregulär entwickelt. Dabei kann das Verhalten des Systems bei bestimmten Anfangswerten (bzw. in deren Nachbarschaft) völlig regulär sein, wenn es sich z. B. um einen periodischen Orbit handelt.

Jede auch noch so kleine Änderung der Anfangswerte kann jedoch nach hinreichend langer Zeit zu einem ganz anderen Verhalten führen, das auch vollkommen unregelmäßig erscheinen kann. Um das Systemverhalten für eine bestimmte zukünftige Zeit berechnen zu können, müssten die Anfangsbedingungen deshalb mit unendlich genauer Präzision bekannt sein und berechnet werden, was praktisch unmöglich ist. Obwohl auch solche Systeme deterministisch und damit prinzipiell bestimmbar sind, sind daher praktische Vorhersagen nur für mehr oder weniger kurze Zeitspannen möglich.[4]

Dieses Phänomen ist auch unter dem Schlagwort Schmetterlingseffekt in der Öffentlichkeit bekannt geworden, wonach selbst der schwache Flügelschlag eines sehr weit entfernten Schmetterlings auf lange Sicht zu einem anderen Ablauf des großräumigen Wettergeschehens führen kann.

Quantentheorie, Determinismus und Unschärfe

Im Folgenden wird die Determiniertheit der Quantenmechanik (und ihre Grenzen durch die Heisenbergsche Unschärferelation) auf Grundlage der Kopenhagener Deutung erläutert. Für alle anderen Interpretationen der Quantenmechanik, beispielsweise die De-Broglie-Bohm-Theorie, ist der folgende Abschnitt nur begrenzt korrekt.

Während im Sinne der klassischen Physik die Vorhersagbarkeit realer komplexer Systeme an praktisch nie vollkommen exakten Messungen der Anfangsbedingungen scheitert, zeigt die Berücksichtigung der Erkenntnisse der Quantenphysik, dass deren Verhalten prinzipiell nicht determiniert ist. So besagt die Heisenbergsche Unschärferelation, dass Ort und Impuls eines Objektes nicht gleichzeitig beliebig genau bestimmbar sind; diese Einschränkung bezieht sich nicht auf Unzulänglichkeiten des Beobachtungsvorgangs (z. B. ungenaue Messung), sondern ist prinzipieller Natur. Diese Unschärfe ist bei makroskopischen Systemen gewöhnlich vernachlässigbar. Da ihre Auswirkungen bei chaotischen Systemen jedoch beliebig wachsen, nehmen sie früher oder später makroskopische Dimensionen an (vgl. Schmetterlingseffekt). Bei dem Gerät zur Ziehung der Lottozahlen mit Kugeln ist das bereits nach etwa 20 Stößen der Fall. Die Vorhersagbarkeit chaotischer Systeme scheitert daher spätestens an der Unschärferelation (weil sie verbietet, dass die Anfangsbedingungen beliebig genau gemessen werden können). Das bedeutet, dass reale Systeme – im Gegensatz zu den sie beschreibenden mathematischen Modellen – prinzipiell nicht im klassischen Sinn deterministisch sein können.

Nichtlineare Systeme

Chaotisches Verhalten kann nur in Systemen auftreten, deren Dynamik durch nichtlineare Gleichungen beschrieben wird. Solche Gleichungen sind meist nicht analytisch, d. h. nicht durch Angabe expliziter Größen, sondern nur numerisch lösbar. Ursache des exponentiellen Wachstums von Unterschieden in den Anfangsbedingungen sind dabei oft Mechanismen von Selbstverstärkung beispielsweise durch Rückkopplungen.

Ist durch Reibung hinreichend Dissipation im Spiel, so kann sich in der Regel kein chaotisches Verhalten ausbilden. So könnten beispielsweise bei Jahrmarktsfahrgeschäften, die konstruktionsbedingt zu chaotischem Verhalten neigen, ohne entsprechende Bremsmaßnahmen unerwartete und unzumutbare Beschleunigungsspitzen auftreten.

Dass dissipative Terme nicht ausschließlich stabilisierend wirken, zeigt sich am Beispiel einer Grenzschicht. Mit der linearen Stabilitätstheorie lässt sich zeigen, dass erst der Einfluss der Reibung das Wachstum kleiner Störungen ermöglicht. Dieses exponentielle Anwachsen stellt die erste Phase des laminar-turbulenten Umschlags dar.

Diskrete Systeme

Eine Julia-Menge

Bisher wurde nur das zeitliche Verhalten kontinuierlicher physikalischer Systeme betrachtet. Chaos wird jedoch auch in Modellen studiert, bei denen jeder Zustand durch einen Iterationsschritt diskret in den Folgezustand übergeht, mathematisch: $x_{n}\mapsto x_{n+1}=f(x_{n}).$ Beispiele sind die logistische Gleichung oder die Iterationsvorschrift, die zu Julia-Mengen führt. Dabei können die gleichen Grundphänomene wie bei kontinuierlichen Systemen auftreten.

Im Prinzip lässt sich einem kontinuierlichen System durch die Betrachtung bestimmter aufeinanderfolgender Zustände stets ein diskretes System zuordnen. Ein Verfahren ist die sogenannte Poincaré-Abbildung, mit der Henri Poincaré Ende des 19. Jahrhunderts die Stabilität der Planetenbewegung studierte.

Phänomene

Ein wesentliches Ergebnis der Chaosforschung ist die Entdeckung, dass chaotische Systeme trotz ihres langfristig nicht vorhersagbaren, scheinbar irregulären Verhaltens bestimmte typische Verhaltensmuster zeigen. Da sie bei völlig unterschiedlichen Systemen beobachtet werden, sind sie von universeller Bedeutung.

Seltsame Attraktoren

Ein typisches Phänomen bei chaotischen Prozessen sind sogenannte Seltsame Attraktoren. Für ihr Verständnis betrachtet man die Dynamik des Systems anhand von sogenannten Phasenraumdiagrammen.

Phasenraumdiagramme

Phasenraumdiagramme bieten einen anschaulichen Überblick über die Dynamik eines Systems. Der Zustand des Systems wird dabei zu jedem Zeitpunkt durch einen Punkt in einem Raum dargestellt, dessen Koordinatenachsen durch den Satz von unabhängigen Zustandsgrößen des Systems und deren Geschwindigkeiten gegeben sind. Die Dynamik lässt sich damit als die Bahn dieses Punktes im Phasenraum interpretieren. So wird beispielsweise der Phasenraum eines Pendels durch den Auslenkwinkel und die zugehörige Winkelgeschwindigkeit aufgespannt, und eine periodische Pendelbewegung entspricht einer geschlossenen Kurve um den Koordinatenursprung. Mathematisch lässt sich die Gesamtheit aller möglichen Verhaltensweisen als Strömungsfeld im Phasenraum interpretieren.

Attraktoren

In manchen Fällen streben Systeme mit verschiedenen Anfangsbedingungen zu demselben Verhalten. Die zugehörigen Bahnen im Phasenraum konvergieren dann zu einer bestimmten Bahn, die als Attraktor bezeichnet wird. Bei einem freien Pendel mit Reibung wäre das der Ruhezustand, das heißt der Koordinatenursprung im Phasendiagramm, zu dem alle Bahnen spiralförmig hinstreben. In diesem Fall handelt es sich um einen punktförmigen Attraktor, einen Fixpunkt. Attraktoren können jedoch auch Kurven sein, wie beispielsweise der periodische Grenzzyklus, der sich bei einem Pendel mit Reibung einstellt, das durch eine äußere periodische Kraft zu Schwingungen angeregt wird. Dieses Verhalten ist typisch für dissipative Systeme. Mathematisch betrachtet können Attraktoren immer dann auftreten, wenn die Divergenz des Strömungsfeldes in Bereichen des Phasenraums negativ ist. Fixpunkte und Grenzzyklen mit positiver Divergenz heißen Repeller.

Der seltsame Attraktor

Lorenz-Attraktor in einem dreidimensionalen Phasenraum, dem ein einfaches Wettermodell zugrunde liegt. Der Bahnpunkt kreist links im Uhrzeigersinn und rechts entgegen. Bei jedem Umlauf verbreitert sich das Band der Bahnen auf das Doppelte und wird anschließend bei der Abwärtsbewegung in der Bildmitte in zwei Hälften zerschnitten, wobei die Entscheidung fällt, ob der nächste Umlauf links oder rechts stattfindet. Auf diesem Mechanismus beruht der chaotische Charakter der Bahnen.

Chaotische Systeme können nun eine besondere Form von Attraktoren haben, die als seltsame Attraktoren bezeichnet werden. Obwohl sie sich in einem begrenzten Gebiet des Phasenraumes aufhalten, sind sie zeitlich unendlich lang und nicht periodisch. Bezüglich kleiner Störungen zeigen sie chaotisches Verhalten. Es sind Fraktale mit einer komplizierten und scheinbar irregulären inneren geometrischen Struktur. Sie sind in eine Teilmenge des Phasenraums eingebettet, die eine niedrigere Dimensionalität besitzt als der Phasenraum selbst. Das bedeutet, dass in der Dynamik trotz des chaotischen Charakters nur ein infinitesimaler und damit verschwindender Bruchteil aller möglichen Zustände vorkommt. Der Attraktor selbst hat, wie bei Fraktalen üblich, eine fraktale Dimension, die durch eine gebrochene Zahl dargestellt wird und die damit noch kleiner als die Dimension des Einbettungsbereiches ist.

Das bekannteste Beispiel für einen seltsamen Attraktor ist der Lorenz-Attraktor, den Lorenz bei der Modellierung des Wettergeschehens entdeckte. Ein weiteres Beispiel ist der Rössler-Attraktor, auf den Otto E. Rössler durch die Betrachtung einer Bonbonknetmaschine stieß.

Nach dem Poincaré-Bendixson-Theorem können seltsame Attraktoren erst in Phasenräumen ab drei Dimensionen auftreten. Ursache ist der Umstand, dass Bahnen im Phasenraum, wie bei einem Strömungsfeld üblich, sich nicht kreuzen, was aber für ein chaotisches Verhalten in zwei Dimensionen erforderlich wäre. Seltsame Attraktoren können nur dann auftreten, wenn mindestens ein Ljapunow-Exponent negativ und mindestens einer positiv ist. Der negative sorgt in gewissem Sinne für Konvergenz bezüglich einer Dimension und damit für die Reduktion der Dimensionalität, der positive für das chaotische Verhalten.

Schnittflächen durch den Phasenraum, die senkrecht von Bahnen durchstoßen werden, werden als Poincaré-Abbildung bezeichnet. Im Fall von seltsamen Attraktoren bilden die Durchstoßpunkte Cantor-Mengen.

Auch bei diskreten chaotischen Systemen werden seltsame Attraktoren beobachtet wie beispielsweise der Hénon-Attraktor. Analog zu attraktiven Strukturen können auch repulsive Strukturen auftreten, die ebenfalls fraktal sind, wie beispielsweise die Julia-Mengen.

Störungen und Resonanzen

Systeme können sehr empfindlich auf Störungen reagieren und dadurch schnell ins Chaos übergehen. Erst das KAM-Theorem hat gezeigt, dass regelmäßige Einflüsse an sensiblen Stellen im Phasenraum nicht zwingend chaotisches Verhalten hervorrufen müssen. Sensibel sind z. B. rationale (ganzzahlige) Verhältnisse zwischen einer ungestörten Schwingung (z. B. eines Doppelpendels) zu einer periodischen Anregung. Diese rufen nämlich Resonanzen hervor (ähnlich wie bei Bahnresonanzen), weshalb für das Theorem nur irrationale Verhältnisse betrachtet werden.

Aus mathematischer Sicht, gerade bei normalerweise vorherrschenden Messungenauigkeiten, kann man jede irrationale Zahl durch Brüche approximieren (Kettenbruchentwicklung). Daher scheint die Überlegung praktisch sinnlos zu sein. Man muss aber bedenken, dass sich ein System umso schneller durch Resonanzen aufschaukeln wird, je näher das Frequenzverhältnis an einem rationalen Wert liegt. Das heißt, die erwarteten Werte weichen noch schneller von den gemessenen ab, als es sonst der Fall wäre.

Besonders stabil gegenüber Störungen (zeitlich gesehen) sind daher irrationale Verhältnisse, die sich nur schlecht durch Brüche annähern lassen. Allgemein spricht man in diesem Zusammenhang von edlen Zahlen, wobei ein Verhältnis namens Goldener Schnitt die Zahl ist, die sich am schlechtesten mittels Kettenbruchentwicklung annähern lässt und somit am stabilsten gegen chaotische Einflüsse ist.

Der Übergang ins Chaos

Nichtlineare dynamische Systeme können neben Chaos auch andere Verhaltensweisen zeigen, wie beispielsweise Konvergenz gegen einen Ruhezustand oder gegen einen periodischen Grenzzyklus. Welches Verhalten auftritt, kann von den Anfangsbedingungen oder auch von anderen Kontrollparametern abhängen. Eine grafische Darstellung der entsprechenden Einzugsgebiete für bestimmte Verhaltensweisen als Funktion dieser Parameter ist oft fraktal. Der Übergangsbereich zu chaotischem Verhalten zeichnet sich dabei durch bestimmte Eigenschaften aus, wie beispielsweise plötzliche qualitative Änderungen des Verhaltens, die auch als Bifurkation bezeichnet werden.

Periodenverdopplung

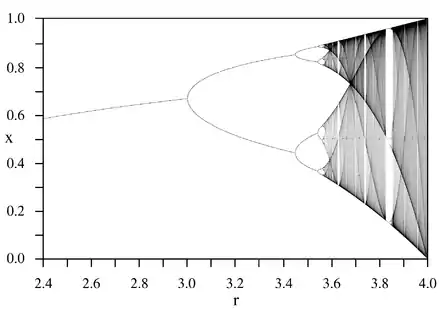
Bifurkationsdiagramm der Zahlenfolge zur logistischen Gleichung. Dargestellt sind die Häufungspunkte x der Folge als Funktion des Kontrollparameters r. Links konvergiert die Folge, rechts ist sie chaotisch, dazwischen periodisch. An den Verzweigungsstellen im Übergangsbereich findet jeweils eine Periodenverdopplung statt.

Beim Übergang von periodischem Verhalten zum Chaos kann ein Phänomen auftreten, das als Periodenverdopplung oder Feigenbaum-Szenario bezeichnet wird. Dabei nimmt zum chaotischen Bereich hin die Oszillationsperiode stufenweise um den Faktor zwei zu ( $\Delta r_{n}\propto 2^{n},$ in nebenstehender Zeichnung). Die zugehörigen Parameterintervalle $\Delta x_{n}$ werden mit zunehmender Periode immer kürzer ( $\Delta x_{n}\propto 1/2^{\delta _{n}}$ ): Das Verhältnis der Längen aufeinander folgender Parameterintervalle ergibt im Limes $n\to \infty$ die Feigenbaum-Konstante $\delta \approx 4{,}669,$ eine irrationale Zahl. Dabei ist der chaotische Bereich auf fraktale Weise immer wieder von Intervallen mit periodischem Verhalten durchbrochen, die jeweils wiederum über Periodenverdopplung in das benachbarte Chaos übergehen. Dieses Verhalten und das zugehörige Zahlenverhältnis hängen nicht von den Details des mathematischen oder physikalischen nichtlinearen Systems ab. Sie sind eine Gemeinsamkeit vieler chaotischer Systeme.

Intermittenz

Neben der Periodenverdopplung werden auch andere Formen des Übergangs ins Chaos beobachtet, wie beispielsweise die sogenannte Intermittenz. Dabei wechseln sich bei einem Parameterwert im Übergangsbereich quasiperiodisches und chaotisches Verhalten ständig ab, wobei zu chaotischen Parameterwerten hin der chaotische Anteil ständig zunimmt.

Beispiele für chaotische Systeme

Naturwissenschaftliche Beispiele

Den meisten Vorgängen in der Natur liegen nichtlineare Prozesse zugrunde. Entsprechend vielfältig sind die Systeme, die chaotisches Verhalten zeigen können. Hier einige wichtige oder bekannte Beispiele:

Das Wetter. Zurzeit ist die Zuverlässigkeit der Wettervorhersage durch die grobe Kenntnis des Ausgangszustandes begrenzt. Aber auch bei vollständiger Information würde eine langfristige Wettervorhersage letztlich am chaotischen Charakter des meteorologischen Geschehens scheitern. Die Stabilität des Wetters kann stark schwanken. So sind bei bestimmten Wetterlagen Vorhersagen für eine Woche durchaus möglich, bei anderen dagegen kaum für 24 Stunden.
Das Doppelpendel. Da es sich aufgrund von nur zwei unabhängigen Freiheitsgraden leicht modellieren und auch leicht herstellen lässt, ist es ein beliebtes Demonstrationsobjekt für überraschende Wechsel im chaotischen Bewegungsablauf. In Computersimulationen und bei den Versuchen lassen sich bestimmte Klassen von Systemverhalten identifizieren, wie beispielsweise die maximal mögliche Anzahl von Überschlägen in Abhängigkeit von der anfänglichen Energie und der Reibung. Bei der schwingenden atwoodschen Maschine liegen ebenfalls zwei Freiheitsgrade vor, aber nur ein Körper schwingt wie ein Pendel.
Das magnetische Pendel, bei dem eine an einem Faden aufgehängte Eisenkugel über mehreren Magneten pendelt.
Systeme mit stoßenden Kugeln. Wichtig ist, dass die Kugeln entweder kollidieren oder an gekrümmten Hindernissen reflektiert werden, damit Störungen exponentiell anwachsen. Beispiele sind das Gerät zur Ziehung der Lottozahlen, der Flipperautomat und Billard.
Das Dreikörperproblem und damit auch unser Sonnensystem oder Sternsysteme aus drei oder mehr Sternen wie beispielsweise Sternhaufen.
In der Medizin sind die Entstehung tödlicher Embolien bei Arterienverkalkung, der Ausfall bestimmter Hirnfunktionen beim Schlaganfall oder die Entstehung bösartiger Tumoren nach Mutationen von Suppressor-Genen typische Beispiele für chaotisches Verhalten.
Der Herzrhythmus wurde zeitweise als chaotisches Signal angesehen. Je nach Gesundheitszustand lässt sich der Herzrhythmus über chaostheoretische Kriterien klassifizieren. Die dabei berechneten Parameter stellen jedoch lediglich empirische Größen dar. Anwendungsgebiete sind die Vorhersage des plötzlichen Herztodes oder allgemein gesprochen die Diagnose von Erkrankungen, die durch das vegetative Nervensystem vermittelt werden. Hierbei wird angenommen, dass das System umso stabiler ist, je chaotischer das Verhalten ist. Die Betrachtung des Herz-Kreislauf-Systems als „chaotisch“ ist jedoch in verschiedener Hinsicht problematisch.
Turbulenz wie beispielsweise beim Bénard-Experiment zur Konvektion.
Die Belousov-Zhabotinsky-Reaktion, eine chemische Reaktion.
Die Populationsdynamik in Räuber-Beute-Modellen.
Die Bäcker-Transformation, ein diskretes System, das den Ort einer Rosine im Kuchenteig beim abwechselnden Auswalzen und Falten des Teigs betrachtet.

Geistes- und sozialwissenschaftliche Beispiele

Neben diesen naturwissenschaftlichen Beispielen wird die Chaosforschung auch in verschiedenen Geistes- und Sozialwissenschaften genutzt, um chaotisches Verhalten zu beschreiben und zu erklären. Hier einige Beispiele:

Börsenkurse und Konjunkturentwicklung. Bereits Mandelbrot hatte darauf hingewiesen, dass zahlreiche Verlaufskurven von Wirtschaftsdaten nichtlineare Eigenschaften haben und sich mit Hilfe von Fraktalen und Intermittenzen beschreiben lassen.[5][6]
In der Geschichtswissenschaft wird die Chaosforschung vor allem zur Beschreibung und Erklärung von Krisen und Übergangszuständen genutzt.[7][8]
In der Kommunikationswissenschaft wird die Chaosforschung im Bereich der Nachrichtenforschung verwendet, um die Auswahl und Gestaltung von Nachrichten besser zu erklären.[9]
In der Psychologie dient die Chaosforschung als Ansatz, um beispielsweise sprachpsychologische Befunde zum Stottern[10] oder die Ursachen für kriminelle Affekttaten (wie Amokläufe)[11] zu erklären.

Allerdings wird in manchen Fällen die Verwendung von chaostheoretischen Begriffen in Geistes- und Sozialwissenschaften kritisiert. Der Vorwurf lautet, dass dabei Begriffe und Ergebnisse der Chaostheorie zur jeweiligen Argumentation herangezogen werden, obwohl die mathematische/physikalische Definition eines chaotischen Systems nicht oder nur teilweise erfüllt ist. Es wird also das Ansehen von Mathematik und Physik in Anspruch genommen, ohne dass ein inhaltlicher Zusammenhang besteht, ähnlich dem Vorgang des Namedropping in der Wissenschaft.

Geschichte

Ende des 19. Jahrhunderts gewann Henri Poincaré einen Preis mit dem Lösungsansatz für die Frage, ob das Sonnensystem stabil sei. Manche Quellen geben dies als die Geburtsstunde der Chaosforschung an, es dauerte jedoch bis in die Mitte des 20. Jahrhunderts, bis der Lösungsansatz von Poincaré mit Hilfe von Computern brauchbar umgesetzt werden konnte.

Chaotische Phänomene sind schon seit langem bekannt, wie beispielsweise das Dreikörperproblem oder Turbulenz. Lange Zeit wurden diese Phänomene als eher weniger verbreitete Spezialfälle angesehen. Da eine angemessene Untersuchung ohne Computer wenig erfolgversprechend schien, und kaum jemand besondere Erkenntnisse erwartete, da die Phänomene vollständig auf den Konzepten der klassischen Physik beruhen, wurden sie wenig beachtet. Das änderte sich erst mit dem Aufkommen schneller Computer.

In den 1960er Jahren entdeckte Edward N. Lorenz die Phänomene, die heute als deterministisches Chaos bezeichnet werden, an einem Modell für das Wetter mit einem Gleichungssatz von drei Gleichungen zur Strömungsmechanik. Als er, um Zeit zu sparen, gerundete Werte einer früheren Berechnung verwendete, beobachtete er, dass winzige Änderungen der Anfangsbedingungen nach kurzer Zeit zu völlig unterschiedlichen Ergebnissen führten. Der daraus abgeleitete Schmetterlingseffekt und die Formulierung des Begriffs der sensiblen Abhängigkeit von Anfangsbedingungen wurden zu häufig missdeuteten Metaphern der „Chaostheorie“.

Robert May simulierte 1976 eine Fischpopulation $P$ mit einer Wachstumsrate $R$ mit der Formel $P_{\text{neu}}=R\cdot P_{\text{alt}}\cdot (1-P_{\text{alt}}),$ um mit dem Term $1-P_{\text{alt}}$ begrenzte Ressourcen abzubilden. Er wählte für seine rechnerische Simulation eine sehr kleine Anfangspopulation von 2 % und entdeckte, dass bei einer Wachstumsrate $R$ um $3{,}8$ ein chaotisches Verhalten seiner Modellrechnung einsetzt.[12]

In den 1970er bis 1980er Jahren entdeckte Mitchell Feigenbaum die Phänomene der logistischen Gleichung und die nach ihm benannte Feigenbaum-Konstante. Diese Gleichung korrespondiert mit der von Benoit Mandelbrot 1980 untersuchten Mandelbrot-Menge, da sie ebenfalls auf einer quadratischen Gleichung beruht.

Etwa zur selben Zeit arbeiteten Siegfried Großmann in Marburg und Hermann Haken in Stuttgart an der Formulierung ihrer Theorien, die bald von den Ideen um Mandelbrot und Feigenbaum inspiriert wurden. Großmann formulierte eine Beschreibung des Lasers mit Hilfe der nichtlinearen Dynamik, und Haken gilt als Begründer der Synergetik und Entdecker des sogenannten Versklavungsprinzips. Die Mandelbrot-Menge, populär „Apfelmännchen“ genannt, gilt als eines der formenreichsten Fraktale, das überhaupt bekannt ist.

Ab den 1980er Jahren wurden an vielen Universitäten Arbeitsgruppen eingerichtet, wie z. B. in Graz, Wien oder Regensburg. In München wirkte die „Chaosgruppe der TU München“ unter der Leitung von Alfred Hübler mit zahlreichen Forschungsprojekten am Lehrstuhl Physik E13 (Edgar Lüscher). Sie organisierte sich nach dem Tod Lüschers in einem Forschungsverein und veranstaltete eine Ringvorlesung und mehrere Jahrestagungen, bei denen versucht wurde, die gesamte Bandbreite der Chaosforschung zu repräsentieren und einen interdisziplinären Dialog zu ermöglichen. Es entstanden auch große Forschungsinstitute wie z. B. das Santa Fe Institute (USA) oder das Institut für nichtlineare Dynamik in Potsdam.

Die aktuelle Forschung befasst sich eher mit einem uneinheitlichen Satz von Phänomenen und Theorien. Viele Forscher, die sich heute noch mit der Thematik beschäftigen, würden sich selbst nicht mehr als Chaosforscher bezeichnen.

Literatur

Herrmann, Dietmar: Algorithmen für Chaos und Fraktale 1. Aufl., Addison-Wesley, Bonn u. a. 1994.
Paul Davies: Prinzip Chaos. Die neue Ordnung des Kosmos. („Cosmic Blueprint“). Goldmann, München 1991, ISBN 3-442-11469-1.
Bruno Eckhardt: Chaos. Fischer, Frankfurt am Main 2004, ISBN 3-596-15569-X.
James Gleick: Chaos, die Ordnung des Universums. Vorstoß in Grenzbereiche der modernen Physik. („Chaos. Making a new science“). Droemer Knaur, München 1990, ISBN 3-426-04078-6.
Günter Küppers (Hrsg.): Chaos und Ordnung. Formen der Selbstorganisation in Natur und Gesellschaft. Reclam, Ditzingen 1996, ISBN 3-15-009434-8.
Wolfgang Metzler: Nichtlineare Dynamik und Chaos, B.G. Teubner, Stuttgart, Leipzig 1998, ISBN 3-519-02391-1
Gregor Morfill, Herbert Scheingraber: Chaos ist überall… und es funktioniert. Eine neue Weltsicht. Ullstein, Frankfurt am Main 1993, ISBN 3-548-35343-6.
Peter Smith: Explaining Chaos.Cambridge University Press, Cambridge 1994. Standardwerk der Philosophie der Chaostheorie.
Marco Wehr: Der Schmetterlingsdefekt. Turbulenzen in der Chaostheorie. Klett-Cotta, Stuttgart 2002, ISBN 3-608-94322-6.
Karin S. Wozonig: Chaostheorie und Literaturwissenschaft. Studienverlag, Innsbruck, Wien 2008, ISBN 978-3-7065-4507-5, Online-Version (PDF).
Heinz Georg Schuster: Deterministisches Chaos. VCH, Weinheim 1994, ISBN 3-527-29089-3.
Otto E. Rössler, Jürgen Parisi, Joachim Peinke und Ruedi Stoop: Encounter with Chaos. Self-Organized Hierarchical Complexity in Semiconductor Experiments. Springer, Berlin 1992, ISBN 3-540-55647-8.

Weblinks

Wiktionary: Chaostheorie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Robert Bishop: Chaos. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Einführung in die Chaos-Forschung. Ehemalige Vorlesung an der Fachhochschule München.
C. Wolfseher: Ein(-)Blick ins Chaos – nichtlineare, dynamische Systeme.
Frank Grotelüschen: Apfelmann im Abseits. Was wurde aus der Chaostheorie? DRadio, 13. November 2005. Mit vier aktuellen Anwendungsbeispielen.
Interaktives Ausprobieren chaotischer Prozesse. Internetseite von Robert Doerner

Einzelnachweise

Ralph Abraham, Yoshisuke Ueda: The Chaos Avant-garde: Memories of the Early Days of Chaos Theory. World Scientific, 2000, ISBN 978-981-02-4404-0. S. 91.
Tito Arecchi, Riccardo Meucci: Chaos in lasers, Scholarpedia 2008
mit $f(t,U)=\{f(t,u)\mid u\in U\}$
Charlotte Werndl: What are the New Implications of Chaos for Unpredictability? (2009). In: The British Journal for the Philosophy of Science. 60, 195–220.
Albert Christmann: Anwendungen der Synergetik und Chaostheorie in der Ökonomie. Karlsruhe 1990.
Otto Loistl, Iro Betz: Chaostheorie. Zur Theorie nichtlinearer dynamischer Systeme. München 1993.
Bernd-Olaf Küppers: Chaos und Geschichte. Läßt sich das Weltgeschehen in Formeln fassen? In: Reinhard Breuer (Hrsg.): Der Flügelschlag des Schmetterlings. Ein neues Weltbild durch die Chaosforschung. Herne 1993.
Walter L. Bühl: Sozialer Wandel im Ungleichgewicht. Zyklen, Fluktuationen, Katastrophen. Stuttgart 1990.
Stefan Frerichs: Journalismus als konstruktives Chaos. In: Martin Löffelholz, Liane Rothenberger (Hrsg.): Handbuch Journalismustheorien. Wiesbaden 2016, S. 191 ff.
Rainer Höger: Chaos-Forschung und ihre Perspektiven für die Psychologie. In: Psychologische Rundschau. 43. Jg., Heft 4, Göttingen 1992, S. 223 ff.
Thomas Fabian, Michael Stadler: A chaos theoretical approach to delinquent behavior in psychosocial stress situations. In: Gestalt Theory, An international multidisciplinary journal. 13. Jg., Heft 2/1991, Opladen 1991, S. 98 ff.
Robert M. May: Simple Mathematical Models with Very Complicated Dynamics. Nature 261 (1976) 459–467.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[AbrahamUeda2000-1] Ralph Abraham, Yoshisuke Ueda: The Chaos Avant-garde: Memories of the Early Days of Chaos Theory. World Scientific, 2000, ISBN 978-981-02-4404-0. S. 91.

[2] Tito Arecchi, Riccardo Meucci: Chaos in lasers, Scholarpedia 2008

[3] t $f(t,U)=\{f(t,u)\mid u\in U\}$

[4] Charlotte Werndl: What are the New Implications of Chaos for Unpredictability? (2009). In: The British Journal for the Philosophy of Science. 60, 195–220.

[5] Albert Christmann: Anwendungen der Synergetik und Chaostheorie in der Ökonomie. Karlsruhe 1990.

[6] Otto Loistl, Iro Betz: Chaostheorie. Zur Theorie nichtlinearer dynamischer Systeme. München 1993.

[7] Bernd-Olaf Küppers: Chaos und Geschichte. Läßt sich das Weltgeschehen in Formeln fassen? In: Reinhard Breuer (Hrsg.): Der Flügelschlag des Schmetterlings. Ein neues Weltbild durch die Chaosforschung. Herne 1993.

[8] Walter L. Bühl: Sozialer Wandel im Ungleichgewicht. Zyklen, Fluktuationen, Katastrophen. Stuttgart 1990.

[9] Stefan Frerichs: Journalismus als konstruktives Chaos. In: Martin Löffelholz, Liane Rothenberger (Hrsg.): Handbuch Journalismustheorien. Wiesbaden 2016, S. 191 ff.

[10] Rainer Höger: Chaos-Forschung und ihre Perspektiven für die Psychologie. In: Psychologische Rundschau. 43. Jg., Heft 4, Göttingen 1992, S. 223 ff.

[11] Thomas Fabian, Michael Stadler: A chaos theoretical approach to delinquent behavior in psychosocial stress situations. In: Gestalt Theory, An international multidisciplinary journal. 13. Jg., Heft 2/1991, Opladen 1991, S. 98 ff.

[12] Robert M. May: Simple Mathematical Models with Very Complicated Dynamics. Nature 261 (1976) 459–467.