Bahnstörung

Eine Bahnstörung ist eine Abweichung der tatsächlichen Flugbahn eines Himmelskörpers von der anhand eines Modells berechneten Flugbahn. Neben der Änderung der Bahn wird auch der verursachende Mechanismus bzw. die Störgröße selbst als Bahnstörung bezeichnet. Grundsätzlich unterscheidet man, neben unregelmäßigen Bahnveränderungen, periodische Bahnstörungen, die Schwankungen um einen Mittelwert beschreiben, und säkulare Bahnstörungen, die langfristige monotone Veränderungen der Bahnelemente darstellen.[1]

Welche Einflüsse als Bahnstörungen zu betrachten sind, hängt somit vom zu Grunde liegenden Modell ab. Im einfachsten Fall wird die Bahn mit Hilfe des newtonschen Gravitationsgesetzes in der Näherung als Zweikörperproblem berechnet und die Bahn durch die sechs Bahnelemente der Keplerbahn beschrieben.[2][3] Für eine genauere Bahnanalyse beispielsweise von Asteroiden werden dagegen routinemäßig die Gravitationskräfte der Sonne, aller Planeten, des Mondes und weiterer größerer Himmelskörper berücksichtigt, ebenso relativistische Effekte.[4] Durch eine Bahnstörung ändern sich die Zahlenwerte der jeweils sechs Bahnelemente (bzw. Satellitenbahnelemente). Dabei werden sie im Allgemeinen auch zeitabhängig. Die Präzession der Knotenlinien, die Drehung der Apsiden und die Drift in den Bahnachsen und Umlaufzeiten sind dann typische säkulare Bahnstörungen. Bei Missionen der Satellitengeodäsie sind im Modell Störgrößen durch das unregelmäßige Erdschwerefeld, durch die Hochatmosphäre, die direkte und indirekte Sonnenstrahlung, sowie der Einfluss von Mond und Sonne (direkt und indirekt über Gezeiten) berücksichtigt.[5][6] Diese Bahnstörungen sind periodisch.

Modell der Keplerbahn

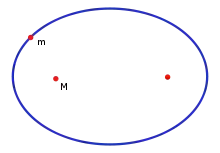
Elliptische Umlaufbahn von m um den Zentralkörper M, dem ersten keplerschen Gesetz zufolge steht M in einem Brennpunkt der Ellipse.

Die Beobachtung des Sternenhimmels mit der Messung und Berechnung der Positionen astronomischer Objekte und die Sammlung in Positionstabellen gehört zu den ältesten Teilgebieten der Astronomie. Auch heute noch werden Bahnen zahlreicher astronomischer Objekte periodisch in den Ephemeriden von renommierten Observatorien veröffentlicht. Damals wie heute sollen Bahnstörungen möglichst integriert sein. Um für den Beobachter auf der Erde möglichst direkt verwendbar zu sein werden auch Effekte wie die Aberration berücksichtigt.

Genauere Erkenntnisse über die mathematische Darstellung der Bahn eines Himmelskörpers veröffentlichte Johannes Kepler im frühen 17. Jahrhundert in Form der später nach ihm benannten keplerschen Gesetze. Diese Gesetze konnten später von Isaac Newton mit Hilfe seines Gravitationsgesetzes theoretisch hergeleitet und damit begründet werden.

Damit traten elliptische Bahnen an die Stelle der bis dahin angenommenen kreisförmigen Planetenbahnen. Für Himmelskörper höherer Energien gibt es noch andere Keplerbahnen als Lösungen des Problems, wie sich ein Himmelskörper um einen anderen (der in der Regel deutlich massereicher ist) bewegt: Parabeln oder Hyperbeln. Keplers Modell beschrieb die Bahnen deutlich besser als die Theorien zuvor. Aber auch sein Versuch, die Bahnen der Himmelskörper vorhersagbar zu machen, basierte auf bestimmten Vereinfachungen: Das eigentlich vorhandene Mehrkörperproblem wird auf ein Zweikörperproblem reduziert. Gravitations- oder andere Kräfte durch die Anwesenheit anderer Himmelskörper kommen also nicht vor. Die betrachteten Himmelskörper werden als Punktmassen mit Zentralfeld angesehen. Weitere Kraftwirkungen durch elektrische oder Magnetfelder, durch Materieströme, Strahlungsdruck, Luftwiderstand, u. ä. werden nicht betrachtet. Weit später entdeckte relativistische Effekte sind ebenfalls nicht berücksichtigt.

Einteilung nach den Ursachen

Gravitative Kräfte

Es gibt verschiedene Arten von Störungen durch Gravitationseinflüsse, die schon auf Grundlage des newtonschen Gravitationsgesetzes verständlich sind. Ursache sind die inhomogene Masseverteilung der Erde oder der gravitative Einfluss anderer Himmelskörper.

Schwerefeldvariationen

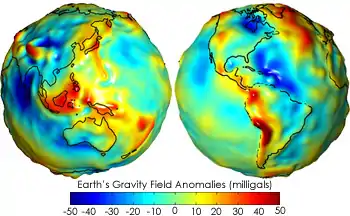
Schwerkraft auf der Erdoberfläche im Vergleich zum idealen Erdellipsoid

Die Beschreibung der Erde als Punktmasse ist stark vereinfachend. In besserer Näherung kann die Erde als ein abgeplatteter Ellipsoid gesehen werden. Somit gilt die Annahme der kugelsymmetrischen Massenverteilung nicht, die bei der Berechnung der Keplerbahn zugrundegelegt wurde. Bis in eine Höhe von mehreren Erdradien werden selbst offene Bahnen (Vorbeiflüge) durch die Erdabplattung messbar gestört. Auch die Abplattung der Sonne, die im Vergleich zur Erde deutlich geringer ausgeprägt ist, trägt zu einem sehr kleinen Teil zu den Periheldrehungen der Planetenbahnen bei.

Erdnahe Satelliten

Bahnelemente eines Himmelskörpers

Niedrig fliegende Satelliten (LEO) spüren Schwereanomalien durch Meere, Gebirge und Unregelmäßigkeiten der Massenverteilung im Erdinnern. Dies nutzt die Satellitengeodäsie aus. Dabei werden selbst die Gezeiten berücksichtigt.

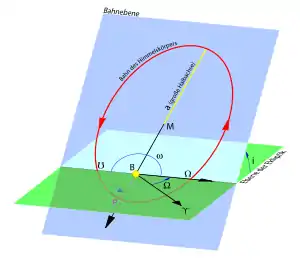
Auf die Bahnebene der Umlaufbahn eines erdnahen Satelliten übt das unregelmäßige Gravitationsfeld der Erde ein Kippmoment aus, dem die Bahnebene durch eine Präzessionsbewegung ausweicht. Diese Ausweichbewegung führt dazu, dass der aufsteigende Knoten bzw. die Knotenlinie nicht feststeht, sondern langsam in der Äquatorebene rotiert und sich damit die Rektaszension des aufsteigenden Knotens $\Omega \$ ständig ändert. Die Bahnebene dreht sich um die z-Achse des astronomischen Koordinatensystems. Gleichzeitig dreht sich die Apsidenlinie in der Bahnebene – ebenfalls durch Schwerkrafteinflüsse – um den Erdmittelpunkt. Damit treten Perigäumsdrehungen auf.

Nur auf vier Positionen hält ein geostationärer Satellit seinen Standort, und nur zwei von ihnen sind stabil: 105°W und 75°O. Kleine Bahnstörungen bewirken einen Drift zu den stabilen Lagen, solche Störungen müssen also ständig korrigiert werden.

Die Auswirkung dieser Bahnstörung kann auch positiv genutzt werden. Es kann durch entsprechende Auswahl der Inklination ein sonnensynchroner Orbit generiert oder das Perigäum über einen festen Erdpunkt gehalten werden. Eine weitere Auswirkung aufgrund der Schwerefeld-Inhomogenitäten der Erde ist die Ost-West-Drift.

Einfluss anderer Himmelskörper

Die Periheldrehung der Bahn eines Planeten. Die Exzentrizität der Bahn und der Betrag der Drehung sind schematisch übertrieben.

Wenn ein Himmelskörper einer Anziehungskraft ausgesetzt ist, welche streng umgekehrt quadratisch mit der Entfernung vom Zentralkörper abnimmt, so würde er sich in klassischer Näherung auf einer Keplerellipse bewegen, deren Form, Lage und Orientierung im Raum unverändert bliebe. Unter der Apsidendrehung versteht man eine fortschreitende Drehung der ganzen Bahn in der Bahnebene. Im Falle der Planetenbahnen ist der Einfluss der jeweils anderen Planeten die Hauptursache für die Periheldrehungen: Aus der Summe der gravitativen Einflüsse der anderen Planeten und der Auswirkung der allgemeinen Relativitätstheorie (siehe weiter unten) resultiert – in eine bezüglich des Fixsternhintergrunds ruhenden Koordinatensystem – eine rosettenartige Bewegung der Planeten: Die anomalistische Periode entspricht nicht genau der siderischen.

Mit steigender Beobachtungsgenauigkeit konnten Anfang des 19. Jahrhunderts Abweichungen der Umlaufbahn des Planeten Uranus von der Keplerbahn präzise bestimmt werden. Als Ursache wurde ein damals noch unbekannter achter Planet des Sonnensystems angesehen, dessen Position aufgrund der Uranus-Bahnstörungen vorhergesagt werden konnte. 1846 führte das schließlich zur Entdeckung des Neptun. In gleicher Weise wurde 1930 der Zwergplanet Pluto aufgrund der von ihm verursachten Bahnstörungen entdeckt.

Auf lange Sicht bewirkt die Gezeitenreibung nicht nur eine Abbremsung der Erdrotation, sondern eine Vergrößerung der Mondbahn. Die mittlere Entfernung zwischen dem Mond und der Erde wächst jährlich um etwa 3,8 cm.

Der Einfluss der direkten Kraftwirkung durch andere Himmelskörper auf ein Objekt in der Erdumlaufbahn hängt von den Orbitparametern ab. Die wesentliche Rolle spielen Mond und Sonne. Dieser Einfluss ist im Bereich geosynchroner Bahnen größer als für stärker gebundene Satelliten. Die Gravitationskraft kann zerlegt werden in eine Komponente parallel und eine senkrecht zur Bahnebene. Die senkrechte Komponente bewirkt eine säkulare, die parallele eine periodische Störung. Die säkulare Störung beeinflusst analog der Erdabplattung die Bahnelemente $i$ , $\Omega$ und $\omega$ . Für geostationäre Satelliten, also $e=i=0$ , verbleibt lediglich eine Auswirkung auf die Inklination. Ohne ausgleichende Korrekturen entsteht mit einer Nord-Süd-Drift von

{\frac {\mathrm {d} }{\mathrm {d} t}}i=0{,}76^{\circ }/{\text{Jahr}}

ein Inclined geosynchronous orbit.

Relativistische Effekte

Gravitationsfeld einer homogenen, nicht geladenen und nicht rotierenden Kugel – vollständige Schwarzschild-Lösung.

In der allgemeinen Relativitätstheorie von Albert Einstein wird die Gravitation als Trägheitskraft gedeutet, sie ist demnach eine geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit. Zur Bestimmung der an einem Punkt herrschenden Krümmung der Raumzeit dienen die einsteinschen Feldgleichungen. Sie wurden so formuliert, dass sie im Grenzfall schwacher Gravitation mit dem newtonschen Gravitationsgesetz übereinstimmen. Innerhalb des Sonnensystems, wo es sich um schwache Felder bzw. geringe Krümmung der Raumzeit handelt, ergeben sich nur geringe Abweichungen von den Vorhersagen des newtonschen Gravitationsgesetzes und damit von den Keplerbahnen. Bei starker Krümmung, wie sie durch starke Konzentration großer Masse auf kleinem Raum hervorgerufen wird, kommen neuartige Phänomene vor, wie sie sich beispielsweise bei Pulsaren im Orbit um andere Sterne zeigen: Der Hulse-Taylor-Doppelpulsar verändert seine Bahn auch dadurch, weil er Energie in Form von Gravitationswellen abstrahlt.

Die Zeitdilatation

Bei der Zeitdilatation handelt es sich nicht um eine Bahnstörung im eigentlichen Sinn, sie hat jedoch Auswirkungen auf die technische Anwendung von Satelliten, so dass dieser Effekt für die Analyse von Bahnstörungen wichtig ist. Die Zeitdilatation hängt von zwei Größen ab, zum einen vom Ort im Gravitationsfeld und zum anderen von der Geschwindigkeit des beobachteten Objektes.[7] Das Zeitsignal der GPS-Satelliten muss entsprechend korrigiert werden: In dieser Flughöhe (MEO) hat der gravitative relativistische Effekt (der allgemeinen Relativitätstheorie) eine größere Auswirkung als der geschwindigkeitsbezogene relativistische Effekt (der speziellen Relativitätstheorie), daher laufen die Uhren des Satelliten relativ zu Uhren auf der Erde schneller.

Die Raumkrümmung

Wegen der allgemeinen Relativitätstheorie weicht das Kraftgesetz für Himmelskörper grundsätzlich vom idealisierten invers-quadratischen Verhalten des newtonschen Gravitationsgesetzes ab (wenn auch nur in sehr geringem Ausmaß), so dass ein weiterer Beitrag zu den Periheldrehungen der Planeten entsteht.

Bekanntestes Beispiel für solche relativistischen Effekte ist die Periheldrehung des Merkur. In der Mitte des 19. Jahrhunderts benutzte Urbain Le Verrier Beobachtungen von Merkurdurchgängen für eine besonders genaue Vermessung der Merkurbahn und stellte anhand der verbesserten Daten fest, dass Merkurs Periheldrehung etwas stärker ausfiel als erwartet. Nach den Berechnungen auf Basis des newtonschen Gravitationsgesetzes sollte sie etwa 530 Bogensekunden (") pro Jahrhundert betragen, wobei circa 280" auf den Einfluss der Venus entfielen, circa 150" auf Störungen durch Jupiter und circa 100" auf die restlichen Planeten. Die beobachtete Periheldrehung (moderner Wert: 571,91" pro Jahrhundert) war jedoch deutlich größer, die Diskrepanz beträgt 43,11". Erst der relativistisch berechnete Anteil von 42,98" zur Periheldrehung stimmt recht gut mit dem beobachteten Überschuss überein.

Der Lense-Thirring-Effekt

Ein weiterer relativistischer Effekt ist der Lense-Thirring-Effekt. Anschaulich gesprochen bewirkt eine rotierende Masse durch eine Mitführung der Raumzeit eine Verdrillung der Raumzeit. Wenn ein Himmelskörper auf seiner Bahn rotiert, führt das also zu einer zusätzlichen Präzession. Die Satellitenmission Gravity Probe B bestätigte 2004/05 diesen Effekt. Eine andere Konsequenz des Effekts wäre, dass die Orbitalebene der Sterne, die nahe einem supermassiven Schwarzen Loch kreisen, zur Präzession um die Drehachse des Schwarzen Lochs gebracht würde. Dieser Effekt konnte noch nicht nachgewiesen werden, ein Nachweis wird jedoch in den nächsten Jahren erwartet. Durch einen Vergleich der Präzession von zwei Sternen auf verschiedenen Orbits sollte es prinzipiell möglich sein, das „no-hair-theorem“ der allgemeinen Relativitätstheorie zu bestätigen.

Wechselwirkung mit der Atmosphäre

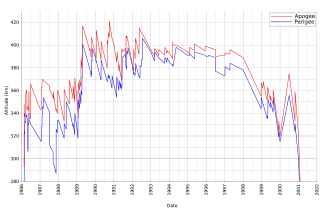
Bahnhöhe der Raumstation Mir während ihrer 15-jährigen Mission: Zu Beginn des 22. Sonnenfleckenzyklus wurde die Mir in einen höheren Orbit verlegt, um so den Aufwand zum Anheben der Umlaufbahn zu reduzieren.

Bei künstlichen Satelliten in niedrigen Orbits ist die Erdatmosphäre nicht zu vernachlässigen. Bei der Wechselwirkung handelt es sich nicht um eine Strömung; die Teilchen treffen einzeln auf. Da sie abprallen und auch Oberflächenatome herausschlagen, tritt je nach Neigung der getroffenen Fläche auch eine Kraft quer zur Flugrichtung auf. Die weit überwiegende parallele Kraftkomponente führt zu einem stetigen Verlust an Bahnenergie, der bei längeren Missionen ausgeglichen werden muss, um einen Absturz zu vermeiden, siehe das Diagramm zur Raumstation Mir in 300 bis 400 km Höhe. Das Hubble-Weltraumteleskop in etwa 600 km Höhe sank dagegen in 19 Jahren um nur rund 80 km.

Das Ausmaß des Effekts ist nur grob vorauszuberechnen, da die Ausdehnung der Hochatmosphäre stark von der Sonnenaktivität abhängt. Eine überschlägige Berechnung erfolgt mit Hilfe der bremsenden Kraft $F_{D}$ :

F_{D}={\frac {1}{2}}c_{w}A\rho v^{2}

wobei:

$c_{w}$ – ist der Widerstandsbeiwert für freie Molekularströmung und liegt zwischen 2,2 und 2,5[8]
A – Fläche senkrecht zu Flugrichtung
$\rho$ – Luftdichte in entsprechender Höhe
v – Geschwindigkeit des Objektes

Die Störgröße kann auch zu Gunsten einer Raumfahrtmission als Aerobraking-Manöver eingesetzt werden.

Strahlungsdruck

Auch der Strahlungsdruck kann zu Bahnstörungen führen. Wenn ein Körper elektromagnetische Strahlung (also auch Licht) absorbiert, reflektiert oder emittiert, dann wirkt sich der entsprechende Impulsübertrag auf seine Bahn aus. Bei Absorption und Emission ist der Strahlungsdruck gleich der Bestrahlungsstärke dividiert durch die Lichtgeschwindigkeit. Bei vollständiger Reflexion ist der Strahlungsdruck doppelt so groß.

Im Bereich der Erdbahn ist $S=1372\;{\text{W}}/{\text{m}}^{2}$ die (gemittelte) Intensität der Sonnenstrahlung. Mit der Lichtgeschwindigkeit $c$ berechnet sich der Strahlungsdruck $p$ wie folgt:

p=(1+r){\frac {S}{c}}=(1+r)\cdot 4{,}6\cdot 10^{-6}\,\mathrm {N} /\mathrm {m} ^{2}

Er ist abhängig von der Größe der bestrahlten Fläche und von deren Reflexionsfaktor $r$ und wirkt als Kraft, die kontinuierlich von der Strahlungsquelle weg gerichtet ist. Bei einem typischen GPS-Satelliten führt der Strahlungsdruck der Sonne zu einer Beschleunigung in der Größenordnung 10⁻⁷ m/s² und damit einem Positionsfehler von einigen hundert Metern pro Tag.[9]

Neben der direkten Sonnenstrahlung wirkt gegebenenfalls auch das von einem anderen Himmelskörper wie der Erde reflektierte Sonnenlicht.

Beim Poynting-Robertson-Effekt wirkt sich der Strahlungsdruck der Sonne auf die Umlaufbahnen kleiner Teilchen der interplanetaren Materie so aus, dass sich diese immer mehr der Sonne annähern.

Neben Licht aus der Umgebung kann auch die von Satelliten zur Kommunikation ausgesendete elektromagnetische Strahlung zu deutlichen Bahnstörungen führen. Besonders bei Kommunikationssatelliten mit hoher Sendeleistung und Richtantennen (beispielsweise Parabolantenne, Phased-Array-Antenne) macht sich diese Störung mit einer Beschleunigung in der Größenordnung 10⁻⁹ m/s² bemerkbar.[9]

Wärmestrahlung

Neben dem direkten Strahlungsdruck macht sich die Strahlungsabsorption auch indirekt bemerkbar. Die daraus resultierende Erwärmung des Objekts führt zu einer zusätzlichen, meist ungleichmäßigen Emission von Wärmestrahlung. Solche Störungen sind insbesondere bei kleineren Körpern mit ihrem hohen Verhältnis von Oberfläche zu Masse relevant.

Die anisotrope Emission von Wärmestrahlung (von der Vorderseite des Flugkörpers) gilt auch als Ursache der Pioneer-Anomalie, der Bahnabweichung der Anfang der 1970er Jahre gestarteten Sonden Pioneer 10 bzw. Pioneer 11.

Beim Jarkowski-Effekt wirkt sich die unterschiedlich starke Erwärmung der sonnenzu- bzw. -abgewandten Seiten eines Asteroiden so aus, dass die verschieden starke Wärmestrahlung in die verschiedenen Raumrichtungen eine je unterschiedliche Kraft auf den Himmelskörper bewirkt. Die Stärke des Effektes hängt dabei auch von der Rotation, der Oberflächenbeschaffenheit (insbesondere der Albedo) und der Wärmeleitfähigkeit des Asteroiden ab. Als Folge werden beispielsweise die Bahnen von Asteroiden, die sich in Richtung ihrer Flugbahn um die eigene Achse drehen (prograd), nach außen gedrückt und die jener, deren Eigendrehung entgegen der Flugbahn (retrograd) verläuft, nach innen verändert. Ein entsprechender Effekt hinsichtlich des Rotationszustandes eines Himmelskörpers ist der YORP-Effekt.

Elektromagnetische Wechselwirkung

Die Magnetosphäre der Erde (künstlerische, nicht maßstäbliche Darstellung)

Für elektrisch geladene oder magnetische Objekte spielt die elektromagnetische Wechselwirkung eine besondere Rolle. Auch außerhalb der Magnetosphäre derjeniger Himmelskörper, die selbst ein planetares Magnetfeld besitzen, existiert durch die Sonne ein interplanetares Magnetfeld, welches durch den Sonnenwind verstärkt wird. Aufgrund der Wechselwirkung zwischen den Magnetfeldern bzw. mit den dazu relativ bewegten elektrischen Ladungen der Objekte wirken weitere Kräfte, die eine Bahnstörung hervorrufen können.

Berechnung gestörter Bahnen

Sofern die störenden Kräfte quantitativ bekannt sind, lässt sich eine gestörte Bahn berechnen. Umgekehrt lässt sich durch die genaue Beobachtung einer Bahn auf störende Kräfte schließen. In beiden Fällen wird eine der folgenden Rechenmethoden verwendet.

Analytische Verfahren

Falls die Situation näherungsweise ein Zweikörperproblem darstellt, also der betrachtete Körper im Wesentlichen an einen dominierenden Massepunkt gebunden ist und Störeinflüsse sich zu wenigen einfachen Termen zusammenfassen lassen, ist eine sogenannte Störungsrechnung möglich. Diese geht von der Kepler-Bahn aus und integriert die Störeinflüsse bzw. die relativistischen Korrekturen über einen Umlauf. Es ergeben sich Änderungsraten der Bahnelemente, etwa eine Periheldrehung. Für mehrere Körper, die sich gegenseitig stören, ist das Verfahren ebenfalls geeignet.

Besonders einfach sind Situationen ohne Bahnresonanzen, wenn also die Umlaufperioden zueinander nicht im Verhältnis kleiner ganzer Zahlen stehen. Die bloße Nähe zu einer Resonanzbedingung ist umso unkritischer, je geringer das Niveau der Störung ist, denn dann ändert sich die Phase der Störung, bevor eine wesentliche Wirkung eingetreten ist. Ohne Resonanzen lassen sich die störenden Körper als über ihre jeweilige Bahn verschmierte Masseringe ansetzen. Das oben für nur einen Umlauf erhaltene Ergebnis gilt dann für viele Umläufe.

Numerische Verfahren

Falls obige Voraussetzungen nicht erfüllt sind, werden die Bahnen nach der Methode der kleinen Schritte berechnet, z. B. mit einem Runge-Kutta-Verfahren.

Falls sehr viele Massepunkte zu berücksichtigen sind, etwa bei der Begegnung zweier Galaxien, kann unter Umständen eine Finite-Elemente-Methode mit geringerem Rechenaufwand sinnvolle Ergebnisse liefern.

Siehe auch

Kozai-Effekt: Periodische Bahnstörung, verursacht durch die Gravitationswirkung weiterer Himmelskörper, welche beispielsweise die Entstehung irregulärer Satelliten der Planeten, die hohe Anzahl an heißen Jupitern unter den Exoplaneten oder die Entstehung von Blauen Nachzüglern erklärt
Fly-by-Anomalie: Seit 1990 mehrfach aufgetretene kleine zusätzliche Geschwindigkeitszunahme, die Raumsonden bei einem Fly-by an der Erde erfahren haben

Literatur

Dino Boccaletti, Giuseppe Pucacco: Theory of Orbits: Volume 2: Perturbative and Geometrical Methods. Springer, 2010, ISBN 978-3-642-08222-1.
Andrea Milani, Giovanni Gronchi: Theory of Orbit Determination. Cambridge University Press, 2009, ISBN 978-0-521-87389-5 (google.de [abgerufen am 18. November 2017]).
Ernst Messerschmid, Stefanos Fasoulas: Raumfahrtsysteme. Eine Einführung mit Übungen und Lösungen. 3., neu bearbeitete Auflage. Springer, Berlin u. a. 2009, ISBN 978-3-540-77699-4.
Ulrich Walter: Astronautics. (= Physics Textbook). Wiley-VCH-Verlag, Weinheim 2008, ISBN 978-3-527-40685-2.
Wiley J. Larson, James R. Wertz (Hrsg.): Space Mission Analysis and Design. 3. Auflage. 8. Druck. Microcosm Press u. a., El Segundo CA u. a. 2006, ISBN 0-7923-5901-1 (Space Technology Library).
Udo Renner, Joachim Nauck, Nikolaos Balteas: Satellitentechnik. Eine Einführung. Springer, Berlin u. a. 1988, ISBN 3-540-18030-3.
Roger R. Bate, Donald D. Mueller, Jerry E. White: Fundamentals of Astrodynamics. Courier Dover Publications, 1971, ISBN 0-486-60061-0 (google.com [abgerufen am 18. Dezember 2012]).

Weblinks

Kamran Ahmed: Orbital Perturbation. (PDF; 265 kB). 2005. Präsentation
Oliver Baur: Ozeangezeitenlösung aus Bahnstörungen erdnaher Satelliten. (PDF; 830 kB). Diplomarbeit. Geodätisches Institut der Universität Stuttgart und GeoForschungsZentrum Potsdam, 2002.
Julian Daubrawa: Bahnstörungen durch Ozeangezeiten. (PDF; 4,5 MB). Diplomarbeit. Geodätisches Institut Stuttgart, 2007.
M. Eshagh, M. Najafi Alamdari: Perturbations in orbital elements of a low earth orbiting satellite. (PDF; 401 kB). In: Journal of the Earth & Space Physics. Vol. 33, No. 1, 2007, S. 1–12.
Horst Montag: Zu relativistischen Effekten in der Satelliten- bzw. Raumgeodäsie. (PDF; 80 kB). Sitzungsbericht der Leibniz-Sozietät 78/79, 2005, S. 277–290.

Einzelnachweise

Günter Seeber: Satellitengeodäsie: Grundlagen, Methoden und Anwendungen. Walter de Gruyter, 1989, ISBN 3-11-084977-1, S. 96 (google.com [abgerufen am 3. Dezember 2012]).
Max Born: Die Relativitätstheorie Einsteins und ihre physikalischen Grundlagen. BoD – Books on Demand (Nachdruck), 2011, ISBN 978-3-86741-722-8, S. 12– (google.com [abgerufen am 19. Dezember 2012]).
Mathias Scholz: Himmelsmechanik: Astronomie und Astrophysik II. epubli, 2012, ISBN 978-3-8442-2642-3, S. 120– (google.com [abgerufen am 19. Dezember 2012]).
Anwendung des "Standard Dynamical Model" (PDF; 1,4 MB) bei der NASA. Berücksichtigt sind dabei auch Ceres, Pallas und Vesta
Thorsten Mayer-Gürr: Gravitationsfeldbestimmung aus der Analyse kurzer Bahnbögen. (Memento vom 10. November 2013 im Internet Archive) (Dissertation, München 2012; PDF; 5,4 MB)
Christoph Förste: Das Schwerefeld der Erde und seine Vermessung mit Satelliten. (PDF; 423 kB)
Alfred Mischke: Vorlesung zur Veranstaltung Vermessungskunde im WS 2011/12 (Memento vom 28. November 2015 im Internet Archive) (PDF; 423 kB). aufgerufen am 4. August 2012.
Michael Gräßlin: Wiedereintritts-Satellit – Ein Satellit kommt zurück. (Memento vom 11. Juni 2007 im Internet Archive) (PDF; 2,8 MB). Vorlesung, Universität Stuttgart, 2004.
A. Heilmann, Luiz Danilo Damasceno Ferreira, C.A. Dartora, K.Z. Nobrega: Perturbative effects of antenna radiation reaction on artificial satellite orbit. In: Aerospace Science and Technology. Band 23, Nr. 1, Dezember 2012, S. 352–357, doi:10.1016/j.ast.2011.08.012.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Seeber1989-1] Günter Seeber: Satellitengeodäsie: Grundlagen, Methoden und Anwendungen. Walter de Gruyter, 1989, ISBN 3-11-084977-1, S. 96 (google.com [abgerufen am 3. Dezember 2012]).

[2] Max Born: Die Relativitätstheorie Einsteins und ihre physikalischen Grundlagen. BoD – Books on Demand (Nachdruck), 2011, ISBN 978-3-86741-722-8, S. 12– (google.com [abgerufen am 19. Dezember 2012]).

[3] Mathias Scholz: Himmelsmechanik: Astronomie und Astrophysik II. epubli, 2012, ISBN 978-3-8442-2642-3, S. 120– (google.com [abgerufen am 19. Dezember 2012]).

[4] Anwendung des "Standard Dynamical Model" (PDF; 1,4 MB) bei der NASA. Berücksichtigt sind dabei auch Ceres, Pallas und Vesta

[5] Thorsten Mayer-Gürr: Gravitationsfeldbestimmung aus der Analyse kurzer Bahnbögen. (Memento vom 10. November 2013 im Internet Archive) (Dissertation, München 2012; PDF; 5,4 MB)

[6] Christoph Förste: Das Schwerefeld der Erde und seine Vermessung mit Satelliten. (PDF; 423 kB)

[7] Alfred Mischke: Vorlesung zur Veranstaltung Vermessungskunde im WS 2011/12 (Memento vom 28. November 2015 im Internet Archive) (PDF; 423 kB). aufgerufen am 4. August 2012.

[drag-8] Michael Gräßlin: Wiedereintritts-Satellit – Ein Satellit kommt zurück. (Memento vom 11. Juni 2007 im Internet Archive) (PDF; 2,8 MB). Vorlesung, Universität Stuttgart, 2004.

[:0-9] A. Heilmann, Luiz Danilo Damasceno Ferreira, C.A. Dartora, K.Z. Nobrega: Perturbative effects of antenna radiation reaction on artificial satellite orbit. In: Aerospace Science and Technology. Band 23, Nr. 1, Dezember 2012, S. 352–357, doi:10.1016/j.ast.2011.08.012.