Erdrotation
Die Erdrotation ist die Drehbewegung der Erde um ihre eigene Achse. Die Rotationsachse nennt man Erdachse. Die Erde dreht sich nach Osten. Vom Polarstern aus betrachtet dreht sich die Erde entgegen dem Uhrzeigersinn.
.gif)

Der Rotationsvektor der Erde weist gemäß der Rechtsschraubenregel genau nach Erd-Nord, und damit fast genau zum Polarstern. Alle Punkte der Erdoberfläche, ausgenommen ihre zwei Pole, bewegen sich dadurch in die (jeweils lokale) Ost-Richtung. Für einen Beobachter, der mit dem Kopf nach Norden am Boden liegt und die Sterne im Zenit betrachtet, bewegt sich etwa eine erdfeste Mastspitze (gegenüber einem sehr nahen Stern binnen einer Minute sichtbar) ebenfalls nach Osten, das jedoch am Himmel durch die Betrachtung von unten, wie aus dem Erdinneren heraus gesehen, links liegt.
Die durchschnittliche Dauer einer Umdrehung bezüglich des als ruhend angenommenen kosmischen Hintergrundes – der mittlere siderische Tag – beträgt 23 h 56 min 4,0989 s. Dies entspricht der vom IERS festgelegten nominellen mittleren Winkelgeschwindigkeit von 7,292115 × 10−5 rad/s[1] bzw., wenn man diese Winkelgeschwindigkeit mit dem Äquatorradius 6378,137 km multipliziert, einer Umfangsgeschwindigkeit von 465,1 m/s. Als Bezugspunkte für die präzise Messung der Umdrehungsdauer dienen heutzutage unter anderem mittels Radiointerferometrie beobachtete extragalaktische Radioquellen. Bis vor wenigen Jahrzehnten standen jedoch keine ruhenden Referenzpunkte zur Verfügung, die höheren Ansprüchen genügt hätten. Die der Beobachtung zugänglichen Sterne waren wegen ihrer Eigenbewegung nur eingeschränkt geeignet.
In der astronomischen Praxis bezieht man die Umdrehung daher in der Regel auf den Frühlingspunkt, dessen Lage bezüglich der Sterne und Planeten stets berechnet werden kann. Die Zeitspanne, die die Erde braucht, um nach einer Umdrehung wieder dieselbe Stellung bezüglich des Frühlingspunktes einzunehmen, ist ein Sterntag und beträgt nur 23 h 56 min 4,0905 s. Die Präzession der Erde ist der Grund dafür, dass ein siderischer Tag etwa 8 Millisekunden länger ist als ein Sterntag.
Teilt man den Sterntag in 24 h* (Stunden Sternzeit) ein, so ist die Sternzeit ein direktes Maß für den Drehwinkel der Erde. Aus Kenntnis der Sternzeit lässt sich also der aktuelle Himmelsanblick bestimmen. Insbesondere kulminiert für den betreffenden Beobachter um 24 h* der Frühlingspunkt.
Man beachte die nicht ganz konsistente Bezeichnung: Der Sterntag bezieht sich trotz seines Namens nicht auf die Sterne, sondern auf den Frühlingspunkt. Auf die Sterne bezieht sich der siderische Tag. Die englischen Bezeichnungen (festgelegt vom IERS) sind beispielsweise genau umgekehrt: der Sterntag heißt hier sidereal day, während der siderische Tag stellar day heißt.
Sonnentag
.svg.png.webp)
Der Sonnentag ist der Zeitraum von einem Sonnenhöchststand zum nächsten und dient als Basis der alltäglichen Zeitmessung. Er dauert im Mittel 24 Stunden und ist damit etwas länger als ein Sterntag. Der Unterschied zwischen der Länge des Sternentags und der Länge des Sonnentags resultiert aus der jährlichen Bewegung der Erde um die Sonne. Nach einer vollständigen Rotation ist die Erde auf ihrer Bahn fast ein Bogengrad weitergelaufen (360 Grad in ca. 365 Tagen). Um diesen gleichen Winkel muss die Erde sich noch weiterdrehen, bis die Sonne wieder in der gleichen Himmelsrichtung am Himmel zu sehen ist, wie am Tag zuvor. Dies benötigt im Mittel etwa 4 Minuten.
Da die elliptische Erdbahn aber im Laufe des Jahres mit variabler Geschwindigkeit durchlaufen wird und weil die Ekliptik zum Himmelsäquator geneigt ist, sind nicht alle Sonnentage eines Jahres gleich lang. Man unterscheidet daher den wahren Sonnentag als Zeitraum zwischen zwei Sonnenhöchstständen und den stets gleich langen mittleren Sonnentag, dessen Länge den über ein Jahr gemittelten Längen der wahren Sonnentage entspricht. Der mittlere Sonnentag wurde per Definition in 24 Stunden eingeteilt. Daher laufen Uhren nach einer mittleren Sonne, anders als die Sonnenuhren, die naturgemäß die tatsächliche Sonne zur Basis nehmen. Der Zeitunterschied zwischen mittlerer Sonnenzeit und wahrer Sonnenzeit wird als Zeitgleichung bezeichnet.
Rotationsachse
Aufgrund des Trägheitsmoments der Erde ist die Richtung ihrer Rotationsachse im Raum (fast, siehe unten) konstant. Richtung Norden zeigt die Erdachse gegenwärtig auf einen Punkt am Himmel, der knapp ein Grad neben einem Stern des Sternbilds Kleiner Bär liegt. Um diesen Punkt scheint sich für einen irdischen Beobachter auf der Nordhalbkugel der Himmel einmal am Tag zu drehen. Der Punkt heißt daher Himmelsnordpol und der Stern Polarstern. Richtung Süden zeigt die Erdachse derzeit nicht auf einen markanten Stern.
Die Rotationsachse ist um knapp 23,5° gegen die Normale der Erdbahnebene geneigt (Schiefe der Ekliptik). Während des jährlichen Umlaufs der Erde um die Sonne ist daher auf einer Hälfte der Bahn die Nordhalbkugel und auf der anderen Hälfte die Südhalbkugel der Sonne mehr oder weniger zugeneigt. Auf dieser Halbkugel herrscht wegen der stärkeren Sonneneinstrahlung Sommer; die anderen Jahreszeiten ergeben sich entsprechend.
Zeitliche Veränderlichkeit
Physikalische Grundlagen
Aufgrund ihres Drehimpulses vollführt die Erde eine Drehbewegung. Der Drehimpuls ist das Produkt aus der Drehgeschwindigkeit der Erde (ausgedrückt als Winkelgeschwindigkeit) und ihrem Trägheitsmoment.
Da der Drehimpuls eine Erhaltungsgröße ist, kann er nur durch die Einwirkung eines von außen angreifenden Drehmomentes geändert werden. Als Vektor besitzt der Drehimpuls sowohl einen Betrag als auch eine Richtung; Konstanz des Drehimpulses bedeutet daher, dass sowohl die Umdrehungsgeschwindigkeit als auch die Lage der Drehachse im Raum konstant bleiben.
Die auf die Erde einwirkenden Drehmomente sind sehr klein, sodass ihr Drehimpuls und damit auch ihre Drehgeschwindigkeit sowie die Ausrichtung ihrer Drehachse im Wesentlichen konstant bleiben. Bei genauer Messung oder Betrachtung langer Zeiträume lassen sich jedoch zeitliche Veränderungen feststellen.
Die Drehgeschwindigkeit ändert sich,
- wenn sich durch Einwirken eines äußeren Drehmoments der Gesamtdrehimpuls ändert,
- wenn sich der betragsmäßig konstant bleibende Gesamtdrehimpuls in verschiedener Weise auf Untersysteme (Atmosphäre/Erdmantel/Erdkern) umverteilt (die Beobachtungen erfassen nur die Bewegung des Untersystems „Erdmantel mit Erdkruste“),
- wenn sich infolge Verformung (z. B. postglaziale Landhebung) oder Massenumverteilung (z. B. Abschmelzen von Gletschern) das Trägheitsmoment der Erde ändert, sodass trotz gleichbleibenden Gesamtdrehimpulses eine andere Drehgeschwindigkeit resultiert (Pirouetteneffekt).
Die Lage der Rotationsachse im Raum ändert sich, wenn äußere Drehmomente einwirken (Präzession). Da die Symmetrieachse der Erde darüber hinaus nicht exakt mit ihrer Rotationsachse übereinstimmt, führt der Erdkörper kleine Schwingungen um die Rotationsachse aus, sodass deren Durchstoßpunkte durch die Erdoberfläche in einem Bereich von einigen Metern schwanken (Polbewegung).
Kurzfristige Schwankungen
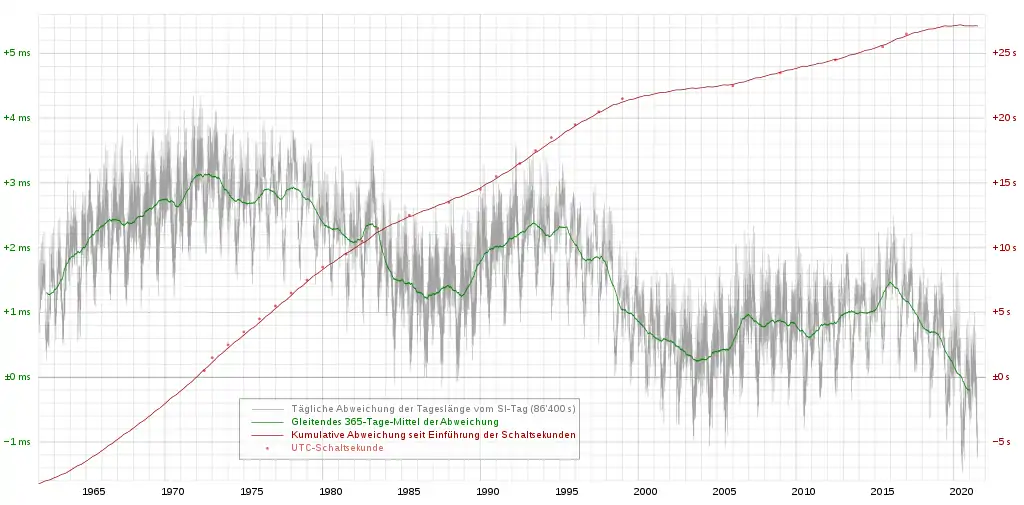
Genaue Messungen zeigen, dass die Dauer einer Umdrehung und damit die Tageslänge nicht streng konstant ist. Das Bild rechts zeigt die Tageslängen seit 1962. Dargestellt ist die Abweichung der gemessenen Tageslänge von einem nominalen, vom internationalen Einheitensystem abgeleiteten Referenztag mit einer Länge von exakt 86.400 SI-Sekunden. Nach einer anfänglichen Zunahme ist der Trend seit Anfang der 1970er Jahre rückläufig. Solche Fluktuationen, die mehrere Jahrzehnte bis Jahrhunderte umfassen können, beruhen vermutlich auf Massenverlagerungen im flüssigen äußeren Erdkern.
Diesen Schwankungen überlagern sich Fluktuationen mit einer Dauer von etwa einem Jahrzehnt. Sie werden vermutlich durch einen Drehimpulsaustausch zwischen Erdkern und Erdmantel verursacht. Auch längerfristige Verschiebungen der Wasser- bzw. Eisverteilung auf der Erdoberfläche dürften eine Rolle spielen.
Besonders deutlich fällt eine jährliche Schwankung mit einer Amplitude von etwa 2 ms auf. Sie lässt sich auf Änderungen in der Position und Stärke der größeren Jetstreams zurückführen. Fluktuationen auf einer Zeitskala von Tagesdekaden werden durch den Drehimpulsaustausch zwischen Erdoberfläche und Atmosphäre verursacht (z. B. Winde, die gegen größere Gebirgsketten wie die Anden oder die Rocky Mountains blasen). Letzterer Zusammenhang ist inzwischen so gut bekannt, dass meteorologische Atmosphärenmodelle benutzt werden können, um diese Schwankungen vorherzusagen (Stichwort: Atmospheric Angular Momentum, AAM).
Gezeitenbedingte Verformungen von Erde und Ozeanen verursachen vierzehntägliche, monatliche, halbjährliche und jährliche Anteile der Fluktuationen. Sie sind völlig vorhersagbar und werden daher oft aus den Beobachtungsdaten herausgerechnet, um die übrigen Effekte klarer hervortreten zu lassen. Sie müssen vor der Anwendung anhand der betreffenden Rechenmodelle wieder hinzugefügt werden.
Gelegentlich werden Einzelereignisse wie z. B. Massenverlagerungen aufgrund starker Erdbeben in den Daten sichtbar. In der Grafik sind die Auswirkungen eines besonders ausgeprägten El Niño im Winter 1982/83 deutlich zu erkennen. Das Seebeben im Indischen Ozean 2004 hat die Erdrotation so beschleunigt, dass sich die Tageslänge um 8 μs verkürzte.[2] Eine weitere Beschleunigung erfuhr die Erdrotation am 11. März 2011 nach dem Erdbeben im Pazifischen Ozean vor der japanischen Küste: Die Erde dreht sich nun etwas schneller, „ein Tag ist nun 1,8 μs kürzer als zuvor“.[3]
Auch Verlagerungen der Biomasse spielen eine gewisse Rolle. Die Behauptung, dass die Erde sich im (Nord-)Sommer langsamer drehe als im Winter, weil die Blätter an den Bäumen das Trägheitsmoment vergrößern (Pirouetteneffekt) und es auf der Nordhalbkugel mehr Bäume gibt als auf der Südhalbkugel, ist jedoch nicht haltbar. Wie die Grafik zeigt, ist die Tageslänge im Nordsommer gerade am kürzesten, die Erde dreht sich dann also besonders schnell. Der sicherlich vorhandene Einfluss des Laubes wird also durch entgegengerichtete größere Effekte völlig überdeckt. Ein überdeckender Effekt ist unter anderem die Umverteilung von Wassermassen in Form von Schnee auf die Höhenlagen der Gebirge.
Bei all diesen Fluktuationen ist zu bedenken, dass sich auch relativ kleine Einflüsse zu merklichen Auswirkungen aufsummieren können, wenn die Einwirkdauer lang genug ist. Bei den längerfristigen Fluktuationen sind daher geringere Drehmomente oder Änderungen des Trägheitsmomentes nötig als bei kürzerfristigen.
Die gegenwärtigen Tageslängen sind meist länger als die Referenz-Tageslänge von 86400 SI-Sekunden. Dies liegt daran, dass die SI-Sekunde letztlich – über mehrere Zwischenschritte – von der Tageslänge abgeleitet wurde, die während der Mitte des 19. Jahrhunderts bestand. Aufgrund der unten erläuterten langfristigen Zunahme der Tageslänge sind die Tage heute generell etwas länger als damals. Der Überschuss der Tageslänge über die nominalen 86.400 s muss regelmäßig durch eine Schaltsekunde ausgeglichen werden. Liegt die Tageslänge beispielsweise längere Zeit um 2 ms über dem Sollwert, so gerät die Erdrotation gegenüber einer konstant gehenden Atomuhr mit jedem Tag um 2 ms mehr in Verzug. Nach 500 Tagen wäre der Unterschied auf eine Sekunde aufgelaufen: Die 500. Rotation wäre also erst um eine Sekunde nach Mitternacht (Atomzeit) des 500. Tages beendet.
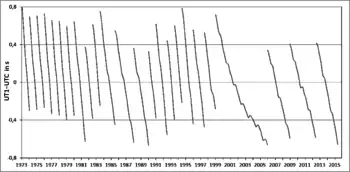
In unregelmäßigen Abständen, zu vollen oder halben Kalenderjahren, wird daher eine Schaltsekunde eingefügt, um die Differenz klein zu halten. Diese Zeitskala, die einerseits auf der durch Atomuhren definierten und daher streng gleichmäßigen SI-Sekunde beruht, die aber andererseits durch Einfügen (oder gegebenenfalls Weglassen) von Schaltsekunden an die unregelmäßige Erdrotation angepasst wird, ist die Koordinierte Weltzeit (UTC). Sie entfernt sich mit jeder positiven Schaltsekunde weiter von der streng gleichmäßigen, aber nur für wissenschaftliche und technische Zwecke benutzten Internationalen Atomzeit (TAI).
Im genannten Beispiel wäre etwa alle anderthalb Jahre eine Schaltsekunde nötig. Dies war während der 1980er Jahre auch tatsächlich der Fall. Wie der Tageslängengrafik zu entnehmen ist, hat sich die Tageslänge seit Mitte der 1990er Jahre wieder deutlich dem historischen Wert angenähert, sodass zwischen 1999 und 2006 keine Schaltsekunde erforderlich war.
Langfristige Änderungen
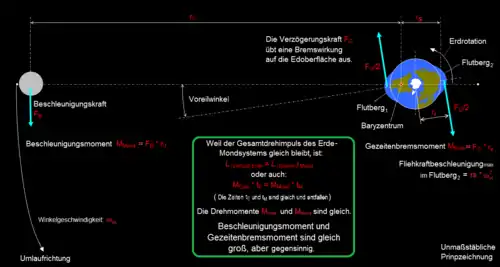
Die Gezeitenreibung übt ein bremsendes Drehmoment auf die Erde aus, sodass die Tageslänge langsam, aber kontinuierlich zunimmt. In den modernen Messreihen wird dieser Effekt fast ganz von den oben beschriebenen Fluktuationen verdeckt. Weil er aber säkular ist und sich daher über längere Zeiträume quadratisch aufsummiert, lässt er sich mit Hilfe überlieferter antiker und mittelalterlicher astronomischer Beobachtungen eindeutig nachweisen und auch für die Vergangenheit zahlenmäßig bestimmen.
Da bis zur Einführung von Atomuhren die vom Beobachter benutzte Zeitskala stets am Sonnenlauf und damit letztlich an der Erddrehung abgeglichen wurde, war sie denselben Fluktuationen und langfristigen Driften unterworfen wie die Erdrotation. Andererseits beruhen moderne physikalische Modelle der Planetenbewegung auf einem streng gleichmäßigen Zeitverlauf, wie er heutzutage unabhängig von der Erddrehung mit Atomuhren realisiert werden kann. Konkret wird hierfür die sogenannte Terrestrische Zeit TT benutzt. Rechnet man nun die Planetenbewegungen zurück, um den Zeitpunkt des beobachteten Ereignisses in der gleichmäßig verlaufenden TT zu bestimmen, und vergleicht diesen Zeitpunkt mit der überlieferten ungleichmäßig verlaufenen Ortszeit des Beobachters, so stellt man eine Diskrepanz fest, die kontinuierlich anwächst, je weiter man in die Vergangenheit zurückgeht. Für babylonische Berichte um das Jahr −700 beispielsweise unterscheidet sich die überlieferte Ortszeit um etwa fünf bis sechs Stunden von jener Zeit, die man unter der Annahme einer konstanten Erdrotation erwarten würde. Auf die den Berichten entnommene Ortszeit ist daher stets eine Korrektur ΔT zu addieren, um den zugehörigen Zeitpunkt in Terrestrischer Zeit zu erhalten und um den Bericht mit der Rückrechnung vergleichen zu können.
Die Auswertung zahlreicher Beobachtungen aus den letzten 2700 Jahren zeigt, dass die Tageslänge während dieses Zeitraums im Mittel um etwa 17 μs pro Jahr zunahm.[4][5] Dies stimmt gut überein mit dem unabhängig davon gewonnenen Befund, dass die Tageslänge einerseits wegen der Gezeitenreibung um etwa 23 μs pro Jahr zunimmt[6] (über die Drehimpulserhaltung abgeleitet aus dem beobachteten Einfluss der Gezeitenreibung auf die Bewegung des Mondes), während die durch die postglaziale Landhebung verursachte Verschlankung der Erde wegen des damit einhergehenden Pirouetteneffektes die Tageslänge um etwa 6,0 μs pro Jahr verkürzt[7] (da das Volumen der Erde sich nicht ändern kann, führt die Hebung polnaher Gebiete zu einer Schrumpfung des Äquatorwulstes – ein Rotationsellipsoid mit geringerer Abplattung hat ein geringeres Trägheitsmoment).
Für prähistorische Zeiten lässt sich die Geschwindigkeit der Erdrotation aus täglichen Wachstumsringen fossiler Meeresorganismen mit Kalkskelett ablesen.[8] Wenn der tägliche Zuwachs durch den monatlichen Wechsel von Nipp- und Springtide oder durch den jährlichen Jahreszeitenwechsel moduliert wird (wie man auch an heute lebenden Verwandten solcher Organismen beobachten kann), so lässt sich durch Abzählen der Ringe zumindest im Prinzip die Anzahl der Tage im Monat beziehungsweise im Jahr ermitteln. Entsprechende Untersuchungen deuten beispielsweise an, dass vor 400 Millionen Jahren das Jahr etwa 400 Tage hatte; bei angenommener gleicher Jahresdauer dauerte ein Tag also nur circa 21,9 Stunden. Für die Zeit vor 310 Millionen Jahren konnte dagegen eine Tagesdauer von 20 Stunden ermittelt werden.
Mathematische Modelle für die frühe, gerade im Entstehen befindliche Erde, also vor rund 4 Milliarden Jahren, legen eine ursprüngliche Tageslänge von lediglich 14 Stunden nahe.[9] Andere Wissenschaftler nehmen für diese Phase der Erdgeschichte eine Rotationsdauer von sechs bis sieben Stunden an.[10]
Präzession und Nutation
Wegen ihrer Abplattung hat die Erde einen 20 km starken Äquatorwulst, der wegen der Schiefstellung der Erdachse gegen die Bahnebene geneigt ist. Die von der Sonne, dem Mond und den anderen Planeten ausgeübten Gravitationskräfte versuchen, ihn in die Bahnebene zu ziehen, doch nach dem Kreiselgesetz der Präzession weicht die Erdachse senkrecht auf dieses Drehmoment aus. Sie behält ihre Neigung von 67° gegenüber der Bahnebene bei, schwenkt jedoch auf einem Kegelmantel in etwa 26.000 Jahren einmal herum.
Weil die Schnittlinie von Äquatorebene und Ekliptik als Ursprung der Himmelskoordinaten dient, ändern sich diese säkular mit der Zeit.
Eine weitere Korrektur ist die Nutation, das Schwingen um die Rotationsachse, mit einer Periode von annähernd 19 Jahren.
Polbewegung
Vor etwa 150 Jahren haben Astronomen herausgefunden, dass geographischer Nord- und Südpol der Erde nicht völlig unveränderlich sind. Zu solchen Verschiebungen kommt es durch Überlagerung mehrerer Phänomene. Zum einen bewegen sich die Kontinente relativ zueinander unter dem Einfluss der Plattentektonik. Aus Sicht eines Messortes auf einem Kontinent verändert sich damit allmählich der Ort der Pole.
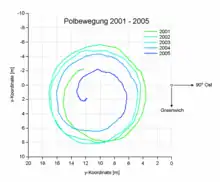
Die Symmetrieachse der Erde fällt nicht genau mit der Rotationsachse zusammen. Die Rotation ist aber trotzdem stabil, da sie wegen der Abplattung der Erde um die Achse mit dem größten Trägheitsmoment stattfindet. Andernfalls würde die Abweichung sich aufschaukeln und zu einem Taumeln des Erdkörpers führen. Wegen der stabilen Situation bleibt die Abweichung aber begrenzt und die Symmetrieachse der Erde vollführt etwa einmal im Jahr eine präzessionsähnliche Bewegung um die Drehachse. Der Punkt, an dem die momentane Drehachse die Erdoberfläche durchstößt, zeichnet dabei eine unregelmäßige Spirale mit einem maximalen Durchmesser von etwa 20 m. Diese Schwingung setzt sich aus zwei Komponenten zusammen: einer durch periodische Verlagerungen von Wasser- und Luftmassen erzwungenen Schwingung mit jährlicher Periode und einer freien Schwingung mit einer Periode von etwa 14 Monaten (Chandler-Periode). Die Überlagerung der beiden führt dazu, dass die Amplitude der Gesamtschwingung in etwa sechsjährlichem Rhythmus zwischen ca. 2 m und ca. 8 m schwankt. Im Mittel driftet der Pol langsam in Richtung 80° West.
Paleographische Untersuchungen legen nahe, dass es in der Vergangenheit auch große Polbewegungen gegeben hat. Einige Bewegungen mit einem Umfang von mehr als 50° fanden vor etwa 800 Millionen Jahren statt.[11][12][13]
Erdrotationsparameter
Für zahlreiche Anwendungen der Astronomie, der Raumfahrt, des Vermessungswesens (insbesondere der Astrogeodäsie) etc. ist die genaue Kenntnis der momentanen Orientierung der Erde im Raum notwendig. Liegen die Genauigkeitsanforderungen in einem Bereich, in dem die oben erläuterten kurz- und langfristigen Schwankungen sich bemerkbar machen, so müssen diese berücksichtigt werden. Zu diesem Zweck werden die sogenannten Erdrotationsparameter regelmäßig gemessen und veröffentlicht. Sie umfassen
- die Weltzeitkorrektur dUT1, die den Unterschied zwischen der an die variable Erddrehung gekoppelten Zeitskala UT1 und der von der gleichmäßigen Atomzeit abgeleiteten Koordinierten Weltzeit UTC angibt. UT1 ist proportional zur Erdrotation und damit ein Maß für den augenblicklichen Drehwinkel der Erde. Der Unterschied dUT1 = UT1 − UTC spiegelt die Unregelmäßigkeit der Erddrehung wider. Droht der Unterschied größer als 0,9 s zu werden, so wird eine Schaltsekunde in UTC eingefügt, um die Abweichung wieder zu kompensieren.
- die Polkoordinaten x und y. Sie beschreiben die Lage der momentanen Drehachse des Erdkörpers (genauer: des Celestial Ephemeris Pole) bezüglich eines bestimmten fixen Punktes auf der Erdoberfläche (des IERS-Referenzpols). Die x-Achse verläuft in Richtung des Nullmeridians (genauer: des IERS-Referenzmeridians) und die y-Achse in Richtung 90° West. Als Maßeinheit werden meist Millibogensekunden verwendet (der Abstand beider Punkte auf der Erdoberfläche lässt sich auch in Metern ausdrücken).
- die Himmelspolschwankungen und , die die beobachteten Abweichungen des Himmelspols von bestimmten mathematischen Modellen für Präzession und Nutation beschreiben. ist die Abweichung in ekliptikaler Länge, ist die Abweichung der Ekliptikschiefe.
Die dafür nötigen regelmäßig weltweit durchgeführten Beobachtungen werden vom International Earth Rotation and Reference Systems Service (IERS) koordiniert, ausgewertet und veröffentlicht.
Die so gewonnenen Daten sind auch selbst von wissenschaftlichem Interesse. Sie enthalten Informationen über den Aufbau und die physikalischen Eigenschaften der Erde, Formänderungen der Erdkugel, Änderungen in der genauen Lage des Erdschwerpunkts und im Erdinneren ablaufende geophysikalische Prozesse.
Die einschlägigen Beobachtungen erfolgten seit dem Ende des neunzehnten Jahrhunderts durch Positionsmessungen an Sternen oder Beobachtungen von Sternbedeckungen durch den Mond. Es konnte alle fünf Tage eine Bestimmung der Parameter vorgenommen werden. Seit den 1970er und 1980er Jahren kamen VLBI-Messungen und GPS-Beobachtungen sowie Laserentfernungsmessungen zu geeigneten Satelliten und zum Mond dazu, und es konnten stündliche oder sogar etwas häufigere Messwerte erfasst werden. Neuerdings lassen sich die Fluktuationen mit Hilfe von Ringlasern auch kontinuierlich verfolgen. Die für die Bestimmung der Erdrotationsparameter benötigten Dreh- und Richtungswinkel können heutzutage mit einer Genauigkeit von etwa einer halben Millibogensekunde gemessen werden. In Mitteleuropa arbeiten einige Forschungsgruppen an dieser Thematik, unter anderem in Hannover (Jürgen Müller) und in Wien (Harald Schuh).
Die Geschwindigkeit, mit der sich die Erdoberfläche in Höhe des Äquators in östliche Richtung bewegt, liegt in etwa bei 1670 km/h und nimmt in Richtung der beiden Pole durch den kleiner werdenden Umfang der Breitenkreise ab.
Entstehung
Nach der gängigen Vorstellung entstand das Sonnensystem aus einer Gas- und Staubwolke, die sich aufgrund ihrer eigenen Schwerkraft verdichtete.
Wenn zwei Gas- oder Staubteilchen sich relativ zueinander bewegen, so hat jedes bezüglich des anderen einen Drehimpuls, sofern sie sich nicht exakt aufeinander zubewegen. Die Existenz eines Drehimpulses ist also nicht an eine Kreisbewegung gebunden; auch ein geradlinig oder sonst beliebig bewegtes Teilchen trägt bezüglich eines Referenzpunktes einen Drehimpuls, sofern seine Bewegung von diesem Referenzpunkt aus gesehen eine Seitwärtskomponente hat, also nicht direkt auf den Referenzpunkt zu gerichtet ist. Man betrachte etwa eine Billardkugel, die eine zweite Kugel nicht völlig zentral trifft. Beide Kugeln werden sich nach der Kollision um ihre Hochachsen drehen; der in diesen Drehungen steckende Drehimpuls wurde dem Drehimpuls entnommen, den die linear bewegte Kugel vor dem Stoß bezüglich der zweiten Kugel hatte. Würden die Kugeln beim Stoß zusammenkleben, so würde das entstandene Objekt rotieren. Aus demselben Grund rotieren auch die in einer Gas- und Staubwolke gebildeten Klümpchen, da es sehr unwahrscheinlich ist, dass alle ihre Bestandteile exakt zentral aufeinandergestoßen sind. Auch nachdem die Klümpchen zu größeren Planetesimalen angewachsen sind, ändert jeder Einschlag eines Planetesimals auf einem Protoplaneten dessen Rotation je nach Einschlagpunkt und -winkel. Die Antwort auf die Frage „Woher kam der Drehimpuls?“ lautet also: aus der ungeordneten Bewegung der Teilchen, die neben ihrem mit der Bewegung verbundenen linearen Impuls auch stets einen Drehimpuls tragen und deren Drehimpulse sich bei der Zusammenballung zu Planeten nicht alle gegenseitig aufgehoben haben. Je kompakter sich der entstehende Körper verdichtet, desto schneller dreht er sich (auch bei konstant bleibendem Drehimpuls) aufgrund des Pirouetteneffektes.
Die Drehrichtung der Erde ist identisch mit der Umlaufrichtung auf ihrer Bahn um die Sonne, wie bei fast allen anderen Planeten auch. Lediglich die Venus dreht sich entgegengesetzt, und die Drehachse von Uranus liegt nahezu in seiner Bahnebene.
Nachweis
Die Rotation der Erde manifestiert sich durch Coriolis- und Zentrifugalkräfte an der Erdoberfläche. Dies zeigt sich unter anderem in der Drehrichtung von Wolkenwirbeln in Tiefdruckgebieten.
Die Erdrotation bewirkt eine mit Annäherung an den Äquator zunehmende Zentrifugalkraft. Sie ist am Äquator der Erdanziehungskraft entgegengerichtet, weshalb dort das Gewicht eines Gegenstands geringer ist als an den Polen. Zusammen mit der ebenfalls durch die Zentrifugalkraft hervorgerufenen Erdabplattung beträgt die Differenz 0,53 %.
Zum Nachweis der Erdrotation im Labor können die folgenden physikalischen Experimente herangezogen werden:
- Foucaultsches Pendel (funktioniert nicht am Äquator; erstmals 1851 in der Pariser Sternwarte)
- Fallexperiment (funktioniert nicht an den Polen)
- Kreiselkompass (funktioniert in einfacher Ausführung nicht an den Polen)
- Lasergyroskop
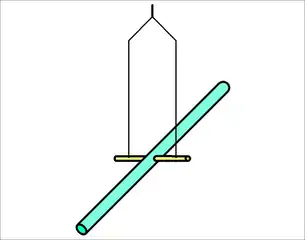 Versuchsbeginn: Stab in Ruhe |
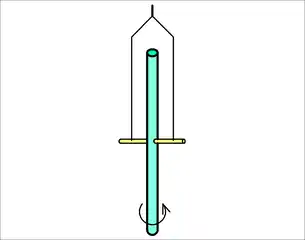 Versuchsende: Stab dreht sich |
- Schwenkbarer idealer Stab (siehe Abbildungen rechts, funktioniert nicht am Äquator)
- Dieser Nachweis gelingt nach Hans Bucka mit einem in einer drehbaren Halterung aufgehängten, schwenkbaren Stab.[14] Ein homogener Stab ist auf der Längsachse dicht neben seinem Mittelpunkt mit einer horizontalen Drehachse reibungsarm gelagert und befindet sich anfangs in horizontaler Lage und in Bezug auf die Erdoberfläche in Ruhe. Dennoch hat er einen Drehimpuls, der durch die Erdrotation bedingt ist. Durch einen geeigneten Mechanismus (zum Beispiel ein durchbrennender Faden, der zwischen der Halterung und dem etwas längeren Stabende gespannt ist) bringt sich der Stab durch das leichte Übergewicht einer Seite in die lotrechte Lage, wobei sich sein Trägheitsmoment um mehrere Größenordnungen verringert. Da der Drehimpuls sich wegen der Drehimpulserhaltung nicht ändert, beginnt sich der Stab im Drehsinn der Erde zu drehen, was zum Beispiel mit einem Lichtzeiger sichtbar gemacht werden kann, dessen Spiegel an der Drehachse der Halterung angebracht wurde.
Literatur
- H. Schuh u. a.: Erdrotation und globale dynamische Prozesse. In: Mitteilungen des Bundesamtes für Kartographie und Geodäsie. Band 32. Frankfurt am Main 2003, ISBN 3-89888-883-5 (Volltext im Portal des Forschungsprojektes „Earth Rotation and Global Dynamic Processes“. (Memento vom 6. Juli 2016 im Internet Archive). [PDF; 3,4 MB; abgerufen am 20. Oktober 2020]).
- Franz Barthelmes, Ludwig Ballani, Roland Klees, Horst Jochmann, Joachim Höpfner, Hans Greiner-Mai (1994): Erdrotationsschwankungen, Erdkerndynamik und Schwerefeld. Geowissenschaften; 12; 300–304, doi:10.2312/Geowissenschaften.1994.12.300.
Weblinks
- Erdrotation.de, Website des Bundesamtes für Kartographie und Geodäsie, abgerufen am 20. Oktober 2020.
- Erik Oppold: Lernmodul „Erde, Erdbahn, astronomische Jahreszeiten“. Geometrisch-astronomische Grundlagen. In: WEBGEO basics / Klimatologie. Institut für Physische Geographie (IPG) der Universität Freiburg, abgerufen am 20. Oktober 2020.
- Erdrotationsdaten des IERS (englisch, französisch und russisch), abgerufen am 20. Oktober 2020.
- Internationaler Erdrotationsdienst IERS: Stellt die gemessene Tageslänge einschließlich historischer Archivdaten seit Beginn systematischer Messungen zur Verfügung (englisch), abgerufen am 20. Oktober 2020.
- Ringlaser der Fundamentalstation Wettzell, abgerufen am 20. Oktober 2020.
- AAM Scientific Background Information. (Memento vom 5. Juli 2009 im Internet Archive). Information zum atmosphärischen Drehimpuls (englisch), abgerufen am 20. Oktober 2020.
- Historical Eclipses and Earth’s Rotation, doi:10.1046/j.1468-4004.2003.44222.x (englisch).
Einzelnachweise
- D. D. McCarthy, G. Petit (Hrsg.): IERS Conventions (2003) (IERS Technical Note No. 32), Kap. 1: General Definitions and Numerical Standards (PDF).
- Chile-Beben hat Erdachse verschoben. In: Spiegel.de. Spiegel-Verlag, 2. März 2010, abgerufen am 20. Oktober 2020.
- Bethge, Philip u. a.: Der Stromausfall. In: Der Spiegel, Nr. 12 vom 21. März 2011, S. 90 f.
- Jean O. Dickey et al. (1994): Lunar Laser Ranging: A Continuing Legacy of the Apollo Program. Science 265, 482–490.
- Warum die Tage länger werden. Spektrum der Wissenschaft, 10/2007, S. 36–45, ISSN 0170-2971.
- F. R. Stephenson: Historical Eclipses and Earth’s Rotation. Cambridge University Press, Cambridge (UK) 1997, S. 37.
- Stephenson, S. 516.
- G. Pannella: Paleontological Evidence on the Earth’s Rotational History since Early Precambrian. Astrophysics and Space Science 16 (1972) 212–237, bibcode:1972Ap&SS..16..212P.
- William und Fank Awbrey: As the World Turns. Can Creationists Keep Time? Thwaites, 1982. S. 18–22 (nach diesem Video).
- Harald Lesch: Wie entstand der Mond? Beitrag für die Sendung alpha-Centauri, abgerufen am 20. Oktober 2020.
- Markus Becker: Unwucht im Globus. In: Spiegel.de. 1. September 2006, abgerufen am 20. Oktober 2020.
- Adam C. Maloof et al.: Combined paleomagnetic, isotopic, and stratigraphic evidence for true polar wander from the Neoproterozoic Akademikerbreen Group, Svalbard, Norway. Geological Society of America Bulletin 188, 2006, S. 1099–2014, doi:10.1130/B25892.1 (online, (Memento vom 15. Oktober 2008 im Internet Archive) abgerufen am 20. Oktober 2020).
- Emmanuelle Arnaud et al. (Hrsg.): The Geological Record of Neoproterozoic Glaciations. Geological Society, London 2011, ISBN 978-1-86239-334-9, eingeschränkte Vorschau in der Google-Buchsuche.
- Hans Bucka: Zwei einfache Vorlesungsversuche zum Nachweis der Erddrehung. Zeitschrift für Physik A, Bd. 126, S. 98–105 (1949), Bd. 128, S. 104–107 (1950).