Satellitenorbit

Ein Satellitenorbit (lateinisch orbis „Kreisbahn“, „kreisförmige Bewegung“, daraus orbita „Gleis“) ist die Umlaufbahn eines Satelliten um einen Zentralkörper (Sonne, Planet, Mond usw.). Dieser Artikel befasst sich mit Satelliten in einer Erdumlaufbahn und deren Flughöhe. Zur genauen Beschreibung der Flugbahn bedarf es weiterer Kenngrößen, die die Artikel Bahnelemente und Satellitenbahnelemente erklären.

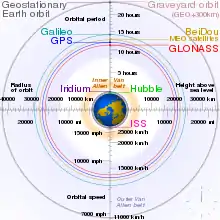
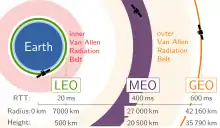
Einige Satellitenorbits im Vergleich: Radius und Höhe, Umlaufdauer und Geschwindigkeit.

Die drei wichtigsten Erd-Orbits und der innere und äußere Van-Allen-Gürtel

Die meisten Raumflüge finden in niedrigen Bahnen (Höhe einige 100 km, Umlaufzeiten um 90 min) um die Erde statt (z. B. Space-Shuttle-Missionen). In mittlerer Höhe (23.000 km, 12 h Umlaufzeit) liegen die Bahnen vieler Navigationssatelliten. Von besonderer Bedeutung ist auch die geostationäre Bahn in 35.800 km Höhe (23 h 56 min 4,09 s Umlaufzeit) mit Bahnneigung 0°. Satelliten in diesem Orbit stehen von der Erde aus gesehen scheinbar fest über einem Punkt des Äquators. Dies ist insbesondere für Kommunikations- und Fernsehsatelliten von Vorteil, da die Antennen nur einmal fest ausgerichtet und dann nicht mehr nachgeführt werden müssen. Durch die Position über dem Äquator ist die Nutzung in den Polarregionen allerdings stark eingeschränkt oder gar nicht möglich.

Entgegengesetzte Forderungen werden an Erdbeobachtungssatelliten oder Spionagesatelliten gestellt. Diese sollen nach Möglichkeit Orte auf der gesamten Erdoberfläche beobachten können, jeweils 10–15 min lang. Dies geht im erdnahen Raum nur in polnahen Umlaufbahnen, wobei hier der sonnensynchrone Orbit (SSO) gegenüber dem direkten Pol-zu-Pol-Orbit vorteilhafter ist. Bei den SSO-Bahnen erleichtert der konstante Sonnenwinkel im Beobachtungsbereich die Auswertung und Klassifikation der gewonnenen Erdbeobachtungsdaten. Die relativ niedrige Umlaufbahn vereinfacht auch das Aufnehmen detailreicher Bilder. Besonders in niedrigen Umlaufbahnen unterliegen die Satellitenbahnelemente raschen Änderungen durch die Erdabplattung.

Arten

Orbits abseits des Äquators

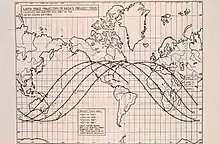
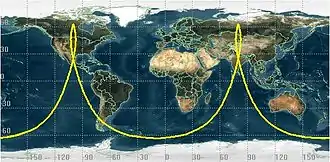
Verschiebung einer Satellitenbahn von Umlauf zu Umlauf

Verläuft ein Orbit nicht exakt über dem Äquator (wie bei geosynchronen Orbits, s. u.), bildet er im einfachsten Fall einen Kreis, dessen Mittelpunkt mit dem Erdmittelpunkt zusammenfällt. (Die folgende Betrachtung gilt darüber hinaus auch für Ellipsenbahnen, die nicht zu exzentrisch sind.) Diese Bahnebene steht in erster Näherung (ohne relativistische Effekte und Störungen von außen) fest im Raum, während sich die Erde mit ihrer täglichen Rotation darunter wegdreht. Auf diese Weise verläuft die „Bodenspur“ des Satelliten in einer charakteristischen Wellenbahn um die Erde, die sich von Umlauf zu Umlauf verschiebt. Bei oberflächennahen Umlaufbahnen (auch LEO, s. u.) beträgt die Umlaufzeit etwa 100 Minuten, so dass sich die Bahn (am besten ablesbar bei den beiden Schnittpunkten der Bahnellipse mit der Äquatorebene) von Umlauf zu Umlauf um rund 25° in westlicher Richtung verschiebt (die Erde hat sich in der Zeit nach Osten darunter weitergedreht). Das entstehende Wellenmuster mit den parallelverschobenen Umlauf-Bodenspuren ist in der Abbildung zu erkennen. Bei einer Kreisbahn ist dieses Muster immer symmetrisch zur Äquatorlinie.

Je steiler die Bahn gegen den Äquator geneigt ist, desto höhere Breiten zu den Polen hin werden in den Extremstellen erreicht.

Parkbahn

Höhe: 150 bis 200 km, unter Umständen auch elliptische Bahnen, die höher oder tiefer reichen.

Eine Parkbahn stellt in der Regel eine mit geringem Antriebsbedarf erreichbare Kreisbahn dar, die die meisten Trägerraketen während des Starts einer Raumsonde zuerst ansteuern. Von dieser kann die Rakete oft leichter in die Bahnebene der Fluchtbahn starten.[1] Nach der Vermessung der beim Aufstieg in die Parkbahn aufgetretenen Ungenauigkeiten wird die Zündung in Richtung Ziel berechnet. Danach verlässt die Rakete, am berechneten Punkt, oft schon während des ersten Umlaufs wieder die instabile Parkbahn. Etliche Raketentypen verwenden Park- oder Zwischenbahnen auch beim Start von Satelliten in höhere Erdumlaufbahnen.

Low Earth Orbit (LEO)

Momentane Sichtbarkeitsbereiche auf der Erdoberfläche am Beispiel zweier Schweizer LEO-Satelliten

(Niedrige Erdumlaufbahn, Erdnahe Umlaufbahn)

Höhe: 200 bis 2000 km[2]
- Höhen zwischen 1200 und 3000 km Höhe sind zwar theoretisch denkbar, werden aber auf Grund der hohen Strahlungsbelastung durch den Van-Allen-Gürtel nach Möglichkeit vermieden.
- LEO-Bahnen sind die energieärmsten Bahnen und damit am leichtesten zu erreichen. Raumfahrzeuge bewegen sich dort mit etwa 7 km/s. Für einen Umlauf um die Erde benötigen sie ca. 100 Minuten. Die Sichtbarkeit und damit der Funkkontakt zu einer Bodenstation beträgt höchstens 15 Minuten pro Umlauf.
Wird genutzt für:
- Bemannte Raumfahrt (beispielsweise Internationale Raumstation ISS; ausgenommen sind die Apollo-Missionen, die vor ihrer Mission zum Mond nur in eine Parkbahn eingeschwenkt sind)
- Spionagesatelliten (beispielsweise amerikanische Keyhole-Satelliten)
- astronomische Satelliten (beispielsweise das Hubble-Teleskop)
- Erderkundungs- und Wettersatelliten
- Amateurfunksatelliten
- Globale Kommunikationssatellitensysteme (etwa Iridium)
- Forschungs- und Technologieerprobungssatelliten (zum Beispiel TUBSAT-N und TET-1)

Sonnensynchroner Orbit (SSO)

Im sonnensynchronen Orbit passiert der Satellit einen Punkt auf der Oberfläche der Erde immer zur selben wahren Ortszeit ±12 Stunden (Ortszeit des aufsteigenden Knotens, engl. Local Time of Ascending Node, LTAN). Die Beobachtungen verschiedener Tage lassen sich leichter vergleichen, da sich bei gleichem Einfallswinkel der Sonnenstrahlen der Schattenwurf und das Reflexionsverhalten von Oberflächen nicht verändert.

Medium Earth Orbit (MEO)

(Mittlere Erdumlaufbahn)

Höhe: 2.000 bis unterhalb 36.000 km
Besonderheiten: Bahnhöhe zwischen LEO und GEO
Wird genutzt für:
- Globale Kommunikationssatellitensysteme wie O3b und O3bmPOWER
- Navigationssatelliten wie GPS, Galileo oder GLONASS

Polare Umlaufbahn

Polare Bahnen verlaufen über die Polregionen, das heißt die Bahnneigung liegt nahe 90°.

Geotransferorbit (GTO)

Höhe: 200–800 km Perigäum, 36.000 km Apogäum
Besonderheiten: Übergangsorbit, um einen GEO zu erreichen (siehe auch Hohmann-Transfer). Das Perigäum wird in den meisten Fällen vom Satelliten selbst angehoben, indem im Apogäum ein Raketenmotor gezündet wird.

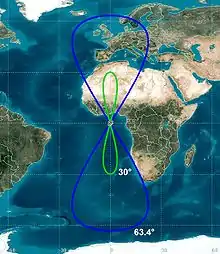
IGSO-Bahnen mit 30° und 63,4° Bahnneigung

Geosynchroner Orbit (GSO, IGSO)

Ein Orbit mit einer Umlaufzeit von 23h56min04s, dessen Bahn nicht notwendigerweise kreisförmig ist oder in der Äquatorebene liegt. Ist sie verkippt, spricht man von einem Inclined geosynchronous orbit (IGSO), ist sie zusätzlich auch hochelliptisch von einem Tundra-Orbit. Der Satellit verharrt zwar auf einer im Mittel konstanten geographischen Länge, seine geographische Breite schwankt aber stark über den Tag, bzw. vollführt genauer gesagt in einem Tag eine sinusförmige Schwingung um den Äquator. Aufgrund von Bahnstörungen, hervorgerufen durch ungleichmäßige Masseverteilung der Erde, gehen geostationäre Satelliten in einen IGSO über, wenn keine Bahnkorrekturen vorgenommen werden.

Geostationärer Orbit (GEO)

Höhe: 35.786 km

Die Kreisbahn eines geostationären Satelliten liegt immer über dem Erdäquator. Die Bahnneigung zum Äquator beträgt 0 Grad. Bei Bahnneigungen größer als null würde der Satellit scheinbar um den Betrag der Neigung senkrecht zum Himmelsäquator pendeln, so dass ein echter stationärer Orbit nur über dem Äquator möglich ist.

Wird genutzt für:
- Meteorologische Satelliten
- Kommunikationssatelliten
- Satelliten für TV-Übertragung wie Astra oder Eutelsat

Die Abkürzung GEO leitet sich von englisch Geostationary Earth Orbit ab.

Einige Raketen wie die russischen Proton, die US-amerikanische Atlas V, Delta IV und Falcon Heavy sowie die europäische Ariane 5 sind in der Lage, Satelliten direkt im geostationären Orbit auszusetzen.

Supersynchroner Orbit

Höhe: Größer als GEO-Orbit

Ein Satellit auf einem supersynchronen Orbit umkreist mit einem Apogäum höher als 35.786 km die Erde langsamer, als sie sich selbst dreht. Bei hoher Einschuss-Inklination kann es günstiger sein, einen geostationären Satelliten statt auf einen GTO-Orbit zunächst auf einen supersynchronen Transferorbit (SSTO) zu platzieren.

Highly Elliptical Orbit (HEO)

Bodenspur eines Molnija-Satelliten

Highly-Elliptical-Orbit-Satelliten (HEO, engl. „Satellit mit hochelliptischer Umlaufbahn“) bewegen sich auf elliptischen Bahnen mit großer Exzentrizität, das heißt großem Verhältnis von Perigäum und Apogäum. Typische Werte sind 200 bis 15.000 km bzw. 50.000 bis 400.000 km. Hochelliptische Erdorbits eignen sich für Forschung, Telekommunikation und militärische Anwendungen. Beispiele sind:

Sehr elliptische Umlaufbahnen für Weltraumteleskope, die sich sehr lange Zeit pro Umlauf über den Van-Allen-Strahlungsgürteln aufhalten sollen (Integral, EXOSAT oder IBEX).
Transferbahn für Raumfahrzeuge, die zum Mond fliegen.
Transferbahn für Raumfahrzeuge, die zu den Lagrange-Punkten L1 oder L2 fliegen.
Molnija-Orbits: Dies sind HEO mit einer Inklination 63,4° (arctan 2) und etwa 12 Stunden Umlaufzeit. Die Inklination, Umlaufzeit, Perigäum und Apogäum für Satelliten der russischen Molnija-Baureihe lauten: 63,4°, 718 Min, 450–600 km, 40.000 km (Apogäum über der Nordhalbkugel). Bei dieser Neigung verschwindet die durch den Äquatorwulst der Erde verursachte Perigäumsdrehung der Bahn, so dass die gewünschte Lage des Apogäums über längere Zeit erhalten bleibt. Satelliten auf Molnija-Bahnen eignen sich bevorzugt für die Versorgung von Polargebieten. Geostationäre Satelliten sind auf Grund der geringen Elevation in diesen Gebieten schlecht und oberhalb von 82° überhaupt nicht mehr zu empfangen. Ein Satellit mit einer Umlaufzeit von 24 Stunden steht für 2 bis 4 Stunden im Erdschatten, für eine ganztägige Abdeckung benötigt man drei Satelliten.[3]

Friedhofsorbit

Mit Friedhofsorbit werden Umlaufbahnen bezeichnet, auf die Satelliten nach dem Ende ihrer Lebensdauer manövriert werden.

z. B. der Orbit ca. 300 km oberhalb der GEO-Orbits

Sonstige Umlaufbahnen

Sehr selten verwenden Satelliten auch Umlaufbahnen, die sich in dieses Schema nicht einordnen lassen. Zum Beispiel liefen die Vela zum Aufspüren von oberirdischen Kernwaffentests auf nur leicht elliptischen sehr hohen Umlaufbahnen zwischen etwa 101.000 und 112.000 km Höhe. Das ist zu hoch für eine MEO-Bahn und zu wenig elliptisch für eine HEO-Bahn.

Von theoretischem Interesse ist die sogenannte Schuler-Periode von 84,4 Minuten. Es ist die kürzest mögliche Umlaufzeit eines Satelliten, der die Erde auf Meereshöhe umkreisen müsste – das ginge aber nur, wenn es weder Berge noch Erdatmosphäre gäbe.

Vereinfachter Überblick der Umlaufbahnen

Orbit	LEO	MEO	GEO	Molnija-Orbits
Höhe	200–500 km	6.000–20.000 km	35.786 km	elliptisch 400–40.000 km
Umlaufzeit	1,5–2 h	4–12 h	24 h	12 h
Empfangsfenster für Funk (bei optimaler geografischer Lage der Bodenstation)	unter 15 min	2–4 h	immer	8 h
zur globalen Versorgung notwendige Anzahl an Kommunikationssatelliten	50–70	10–12	3 (Polargebiete nur bis max. 82° Breite)	6, je 3 für die nördliche und die südliche Halbkugel

Umlaufzeit

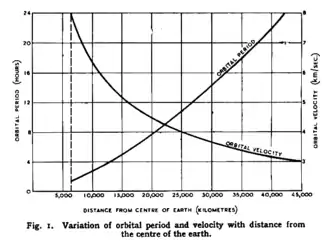
Umlaufgeschwindigkeit in Abhängigkeit von der Bahnhöhe (Clarke 1945).

Die Umlaufzeit $T$ und die äquivalente Bahngeschwindigkeit $v$ in einem Orbit um einen Zentralkörper werden durch die Keplerschen Gesetze bestimmt und können aus

(1)

T={\sqrt {\frac {4\pi ^{2}a^{3}}{G\left(M_{1}+M_{2}\right)}}}

(2)

v={\frac {2\pi a}{T}}\,

berechnet werden. Hierbei bezeichnen

$T$ die Umlaufzeit,
$v$ die äquivalente Bahngeschwindigkeit eines Kreisorbits,
$a$ die große Halbachse,
$M_{1}$ und $M_{2}$ die Massen des Zentralkörpers und des Satelliten,
$G$ die Gravitationskonstante.

Zu beachten ist, dass die Umlaufzeit unabhängig von der Exzentrizität und damit von der kleinen Halbachse der Bahn ist. Alle ellipsenförmigen Umlaufbahnen im selben System mit der gleichen großen Halbachse benötigen die gleiche Umlaufzeit.

Mit einem angenommenen Erdradius von 6371 km, einer Erdmasse 5,974 · 10²⁴ kg und der Gravitationskonstante 6,6742 · 10⁻¹¹ m³kg⁻¹s⁻², sowie einer gegenüber der Erdmasse vernachlässigbaren Satellitenmasse kann die Umlaufzeit aus der Bahnhöhe h über der Erdoberfläche wie folgt berechnet werden:

(1a)

T=166\cdot 10^{-6}\ {\text{min}}\cdot {\sqrt {\left({\frac {h}{1\ {\text{km}}}}+6371\right)^{3}}}

Bei Vernachlässigung der Satellitenmasse vereinfacht sich die Berechnung der Umlaufgeschwindigkeit (Rechengang siehe bei oberflächennahen Umlaufbahnen):

(2a)

v={\sqrt {GM/a}}

mit

G\cdot M=3,987\cdot 10^{14}\ {\text{m}}^{3}/{\text{s}}^{2}

Startort

Für äquatoriale oder äquatornahe Bahnen wie zum Beispiel geostationäre Umlaufbahnen ist ein äquatornaher Startort von Vorteil. Es wird dann relativ wenig Treibstoff für die Bahnkorrekturmanöver benötigt, die den Satelliten in die gewünschte Umlaufbahn bringen. Außerdem hat ein äquatornaher Startort den Vorteil, dass die Nutzlast bereits eine relativ hohe Horizontalgeschwindigkeit von der Erdrotation mitbekommt. Insbesondere die Ariane mit ihrem Startplatz im Raumfahrtzentrum Guayana ist hier im Vorteil, ebenso das Unternehmen Sea Launch mit seiner äquatornahen Seeplattform.

Lebensdauer

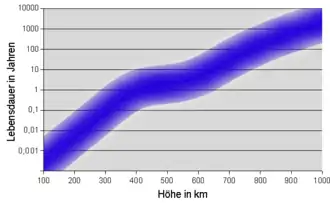
Satellitenverweilzeiten in Abhängigkeit von der Bahnhöhe

Niedrigfliegende Satelliten verweilen nur kurz auf ihrer Umlaufbahn um die Erde. Die Reibung mit der Atmosphäre bremst sie ab und lässt sie auf die Erde stürzen. Bei einer Flughöhe von 200 km bleiben sie nur wenige Tage auf der Umlaufbahn. Niedrigfliegende Spionagesatelliten fliegen aus diesem Grund auf stark elliptischen Bahnen. Sie verglühen erst, wenn sich auch das Apogäum auf ca. 200 km verringert hat.

Die Internationale Raumstation umkreist die Erde in einem Abstand von ca. 400 km und verliert pro Tag 50 bis 150 m Höhe. Ohne Bahnanhebungen (englisch Reboost) würde sie in wenigen Jahren verglühen. Ab einer Höhe von 800 km verbleiben Satelliten mehr als 10 Jahre im All, hochfliegende Satelliten praktisch für immer. Außer Dienst gestellt tragen sie erheblich zum Weltraummüll bei. Das Diagramm veranschaulicht die Verweilzeiten. Je höher die Sonnenaktivität, desto weiter dehnt sich die Atmosphäre aus, desto größer ist ihr Einfluss auf höhere Bahnen. Der Knick in der Kurve veranschaulicht die verringerte Sonnenaktivität alle 11 Jahre.

Auch die Satellitengeometrie beeinflusst die Reibung. Je geringer die Masse und je größer der Strömungsquerschnitt und die Geschwindigkeit relativ zur Atmosphäre (ballistischer Koeffizient), desto größer ist die Reibung, damit die Geschwindigkeitsabnahme und damit die Abnahme der Bahnhöhe. Die Internationale Raumstation richtet während des Fluges durch den Erdschatten ihre drehbaren Solarpaneele so aus, dass der mittlere Widerstand um 30 % verringert wird (sog. Night Glider mode).

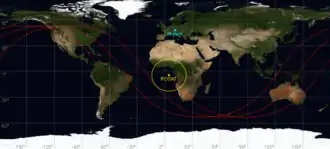
Bodenspur des Satelliten ROSAT bei 5-stündiger Beobachtung (Feb. 2011)

Eine Vorhersage über den Absturzort eines Satelliten auf die Erde ist praktisch nicht möglich. Das Bild zeigt als Beispiel den niedrig fliegenden Satelliten ROSAT, der im Oktober 2011 abstürzte. Während einer 5-stündigen Beobachtung legte der Satellit die als rote Bodenspur markierte Strecke zurück. Die Aufschlagszone für die verschiedenen Trümmerteile bildet immer eine langgestreckte Ellipse in Bahnrichtung. Um den Aufschlagsort auf einen Erdteil einzugrenzen, müsste die Prognose für einen Satellitenabsturz auf 15 Minuten genau sein. Selbst wenige Tage vor dem endgültigen Verglühen sind Bahnstörungen und die Wechselwirkungen mit der Atmosphäre zu groß, um den Einschlagszeitpunkt sinnvoll einzugrenzen. Die Inklination der Satellitenbahn bestimmt, welche Breiten nicht überflogen werden und außerhalb der Risikozone sind. Bei einem polaren Satellit mit fast 90° Inklination ist es die gesamte Erdoberfläche, bei ROSAT mit 53° Inklination der Bereich zwischen 53° Nord und 53° Süd.

Sichtbarkeit mit dem bloßen Auge

Satelliten und andere Objekte in niedrigen Umlaufbahnen sind typischerweise aus Metall hergestellt, so dass sie Licht gut reflektieren. Werden sie von der Sonne angestrahlt, wird genügend Licht reflektiert, sodass sie auch mit bloßem Auge erkennbar sind. Dazu müssen allerdings mehrere Bedingungen erfüllt sein: Auf dem Boden muss es schon dunkel genug sein, damit sich der Lichtreflex vom Himmelshintergrund abheben kann; der Satellit muss aber noch voll von der Sonne angestrahlt sein. Diese beiden Bedingungen sind nur direkt nach Sonnenuntergang oder direkt vor Sonnenaufgang gegeben, wenn es am Boden Nacht ist, aber die Sonne in der Höhe des Satelliten von ihm aus gesehen über dem Horizont steht. Die dritte Bedingung ist, dass der Satellit zu diesem Zeitpunkt auch das Sichtfeld des Beobachters durchqueren muss, das, wie weiter oben ausgeführt, nicht allzu groß ist. Somit erreicht ein Satellit eine bestimmte Region abseits des Äquators nur in größeren Zeitabständen zu den genannten passenden Zeiten, siehe als Beispiel die Erörterungen bei der ISS. Die vierte Bedingung ist einfach, dass die Bewölkung die Sicht nicht versperren darf.

Für den Beobachter entsteht das Problem, solche Satellitenreflexe von Flugzeugen zu unterscheiden. Satelliten erscheinen dabei beträchtlich schneller und gleichförmiger in ihrer Bewegung, sie sind typischerweise nur wenige Minuten im Sichtfeld. Außerdem weisen sie keine Blinklichter auf wie normale Flugzeuge.

Für die ISS und viele andere Satelliten gibt es Webseiten mit Terminangaben[4][5] für kommende Sichtungsmöglichkeiten.

Eine Besonderheit stellen die sogenannten Iridium-Flares dar, die entstehen, wenn die Satelliten des Iridium-Satellitentelefonsystems für einen Augenblick die Sonne genau zum Beobachter reflektieren. Der Effekt ist so außergewöhnlich stark, weil diese Satelliten eine sehr große, ebene, reflektierende Fläche aufweisen. Durch die Außerbetriebnahme älterer Iridium-Satelliten treten die Flares nur noch selten auf und werden voraussichtlich ab Mitte der 2040er Jahre der Vergangenheit angehören.[6]

Literatur

Oliver Montenbruck u. a.: Satellite orbits – models, methods, and applications. Springer, Berlin 2001. ISBN 3-540-67280-X
Byron D. Tapley u. a.: Statistical orbit determination. Elsevier Acad. Press, London 2004. ISBN 0-12-683630-2
Guochang Xu: Orbits. Springer, Berlin 2008. ISBN 3-540-78521-3
F. O. Vonbun u. a.: Orbit determination accuracies using satellite-to-satellite tracking. in: IEEE Transactions on Aerospace and Electronic Systems. Bd. AES-14, Ausg. Nov. New York 1978, S. 834–842. bibcode:1978ITAES..14..834V

Weblinks

Bernd Leitenberger: Umlaufbahnen
AMSAT: Software für die Satellitenbeobachtung (englisch)
Andreas Grieß (Statista)/che: Infografik zu Satelliten: China übertrifft Russland im Orbit, in Spiegel Online

Einzelnachweise

Bruno Stanek: Raumfahrt Lexikon, Halwag Verlag, Bern, Seite 221, 1983, ISBN 3-444-10288-7
What’s So Special About Low Earth Orbit? wired.com, abgerufen am 15. Februar 2016
Hans-Martin Fischer: Europäische Nachrichten-Satelliten Von Intelsat bis TV-Sat. Stedinger Verlag, Lemwerder 2006. ISBN 3-927697-44-3
Heavens-Above – Weltweite Beobachtungsmöglichkeiten der ISS, Iridium Flares und anderer Satelliten
Satellite Sighting Information – Zeiten und Orte der ISS und Shuttles am Nachthimmel über Deutschland
The Iridium Flare Era is About to End. In: Universe Today. 19. März 2019, abgerufen am 30. Juli 2019.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bruno Stanek: Raumfahrt Lexikon, Halwag Verlag, Bern, Seite 221, 1983, ISBN 3-444-10288-7

[2] What’s So Special About Low Earth Orbit? wired.com, abgerufen am 15. Februar 2016

[3] Hans-Martin Fischer: Europäische Nachrichten-Satelliten Von Intelsat bis TV-Sat. Stedinger Verlag, Lemwerder 2006. ISBN 3-927697-44-3

[4] Heavens-Above – Weltweite Beobachtungsmöglichkeiten der ISS, Iridium Flares und anderer Satelliten

[5] Satellite Sighting Information – Zeiten und Orte der ISS und Shuttles am Nachthimmel über Deutschland

[utoday-6] The Iridium Flare Era is About to End. In: Universe Today. 19. März 2019, abgerufen am 30. Juli 2019.