Digitalsignal
Ein Digitalsignal (von engl. digit = Ziffer; durch Ziffern dargestellt) ist ein Signal, welches durch diskrete Werte repräsentiert wird und seine zeitliche Entwicklung beschreibt. Es kann aus einem Analogsignal gebildet werden, welches den zeitlich-kontinuierlichen Verlauf einer physikalischen Größe beschreibt. Die Umwandlung eines Analogsignals in ein Digitalsignal geschieht durch Quantisierung und Abtastung, welche zu definierten Zeitpunkten erfolgt. Digitale Werte sind üblicherweise als Binärzahlen kodiert. Ihre Quantisierung wird somit in Bits angegeben.
Digitalsignale spielen in der Nachrichtentechnik und in der digitalen Signalverarbeitung eine bedeutende Rolle. Beispiele für Digitalsignale sind etwa die Videosignale, die beim DVI- und HDMI-Standard übertragen werden oder die Audiosignale bei Dolby Digital und S/PDIF. Die Datenübertragung über DSL und WLAN, sowie bei den Mobilfunkstandards GSM und UMTS, beruht ebenso auf digitalen Signalen, wie die moderne Computertechnik.
Allgemeines
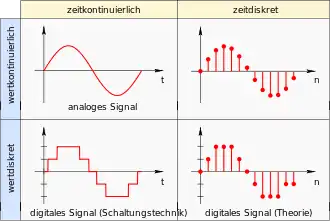
Die Umsetzung eines Analogsignals in ein Digitalsignal erfolgt in zwei Schritten, welche in beliebiger Reihenfolge ausgeführt werden können:
- Die Abtastung, um ein zeitkontinuierliches Signal in ein zeitdiskretes Signal überzuführen.
- Die Quantisierung, um ein wertkontinuierliches Signal in ein wertdiskretes Signal umzuwandeln.
Je nach Anwendungsbereich sind unterschiedliche Begriffsfestlegungen üblich.[1] Die genaue Unterscheidung, was unter einem Digitalsignal zu verstehen ist, ergibt sich üblicherweise aus dem jeweiligen Zusammenhang: In der Signaltheorie werden als Repräsentierung mathematische Folgen verwendet welche anschaulich durch eine „unendlich dünne“ Impulsfolge in der zeitlichen Abfolge gekennzeichnet sind. Hingegen in digitalen Schaltungen, wie sie im Bereich der Digitaltechnik üblich sind, ist eine mathematische Folge durch physikalische Parameter wie eine elektrische Spannung nicht darstellbar: Das Digitalsignal wird in diesem Fall durch einen zeitkontinuierlichen Verlauf gebildet, wobei sich der kontinuierliche Verlauf nur zu bestimmten Zeitpunkten ändert und zwischen den Zeitpunkten im Wert konstant ist.
Die Abtastung und Bildung des Digitalsignals erfolgt üblicherweise in konstanten Zeitintervallen, allerdings ist dies nicht zwingend notwendig.
Signaltheorie
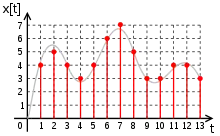
Ein Digitalsignal x[n] kann als eine Folge von Zahlen, welche aus einem abgegrenzten Wertvorrat stammen, beschrieben werden. Der Index n stellt die auf die Abtastrate normierte Zeitvariable dar – üblicherweise erfolgt die Abtastung zu konstanten zeitlichen Abständen Ts. Der Kehrwert wird als Abtastrate oder als Abtastfrequenz fs bezeichnet. In nebenstehender Abbildung ist der beispielhafte Verlauf eines Analogsignals in grau und die daraus gebildete digitale Signalfolge in rot mit den Werten:
- mit dem Index n = 1, 2, …, 13
dargestellt. Wesentlich ist, dass die Werte zwischen den Abtastzeitpunkten nicht Null sind oder andere Werte umfassen, sondern nicht definiert sind. Die Abbildung auf ganze Zahlen ist dabei willkürlich gewählt.
Das Nyquist-Shannon-Abtasttheorem beschreibt in diesem Fall den Effekt, dass in der Folge x[n] nur dann die vollständige Information des analogen Signalverlaufs enthalten sein kann, wenn dessen höchsten Frequenzanteile fa kleiner als die halbe Abtastfrequenz fs sind:
Digitaltechnik
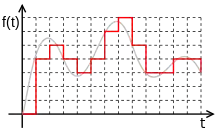
In der Digitaltechnik wird ein Digitalsignal zusätzlich mit einer Sample-And-Hold-Schaltung 0. Ordnung gebildet und stellt dann einen zeitkontinuierlichen Verlauf dar, welcher sich nur zu den einzelnen Abtastzeitpunkten in seinem Wert ändert.
Die einzelnen zeitdiskreten Abtastwerte der Folge werden mit der Rechteckfunktion gefaltet. Daraus entsteht ein Digitalsignal, wie in rot in der nebenstehenden Abbildung beispielhaft dargestellt. Dieser Verlauf f(t) kann, zumindest näherungsweise, beispielsweise durch einen Spannungsverlauf physikalisch in einer Digitalschaltung und in integrierten Schaltungen realisiert werden.
Dabei ist zu beachten, dass durch die Faltung mit der Rechteckfunktion bei der Umwandlung in den ursprünglichen analogen Signalverlauf mittels Digital-Analog-Umsetzer (DAC) eine Verzerrung des Frequenzspektrums auftritt, welche durch entsprechende Filter kompensiert werden muss. Die Verzerrung entspricht der Sinc-Funktion, welche die Fouriertransformierte der Rechteckfunktion darstellt.
Beispiel
Bei der Aufnahme einer Audio-CD wird jeder Kanal (links/rechts) des Quellsignals 44.100-mal pro Sekunde abgetastet. Die Abtastfrequenz ist in diesem Fall 44,1 kHz. Höherfrequente Details des aufgenommenen Quellsignals als die halbe Abtastrate, in diesem Fall also ca. 22 kHz, werden nicht erfasst und bei der Aufnahme durch Antialiasing-Filter entfernt.
Die so gewonnenen einzelnen Abtastwerte (“Samples”) sind noch in ihrer Größe kontinuierlich, das heißt, sie können jeden beliebigen Wert besitzen. Um diese Werte in Zahlenform darstellen zu können, müssen sie zunächst durch Quantisierung, eine Form von Rundung, in ein festes Werte-Raster eingepasst werden. Feinere Änderungen zwischen den Werteraster-Stufen werden nicht erfasst oder erzeugen eine Änderung um eine volle Stufe. Diese Wortbreite, Auflösung wird daher möglichst fein gewählt und umfasst bei der Audio-CD 65.536 mögliche Werte mit einer linearen Kennlinie, d. h., unabhängig von der Signalgröße wird eine konstante Auflösung im Wertebereich verwendet. Die einzelnen Wörter pro Abtastung werden bei der Audio-CD durch die Codierung als Binärzahlen mit 16 Bit pro Wort abgebildet, die Anzahl der Stellen pro Wort wird auch als Dynamik bezeichnet, und stehen dann zur weiteren Verarbeitung, wie der Aufzeichnung auf dem Datenträger, zur Verfügung.
Anwendung
Übertragung
Übertragen werden können nur Signale, die zeitkontinuierlich sind. Weiterhin kommen noch Störungen wie thermisches Rauschen und andere Ungenauigkeiten in Bauteilen hinzu, die es praktisch ausschließen exakt einen bestimmten Wert (repräsentiert durch Spannung, Feldstärke o. ä.) zu übertragen. Das bedeutet, dass jedes digitale Signal nur in Form eines analogen Signals übertragen werden kann und auf Empfängerseite dann wieder digitalisiert werden muss.
Im einfachsten Fall ordnet man jedem möglichen Wert des digitalen Signals einfach einen Wert oder Wertebereich einer physikalischen Größe zu, die man überträgt. In der TTL-Technik wird bspw. (bei positiver Logik) die Binärziffer „0“ durch die Spannung 0 … 0,4 V und die „1“ durch 2,4 … 5,0 V dargestellt.
Solch ein analoges Signal, das plötzliche, schnelle Änderungen im Verlauf aufweist (wie z. B. das oben beschriebene digitale Signal der Schaltungstechnik) hat die unerwünschte Eigenschaft ein sehr breites Spektrum zu besitzen. Das führt zu Störungen in benachbarten Kanälen bzw. es müssen Kanäle mit großer Bandbreite verwendet werden. Deshalb wird bei heutigen digitalen Übertragungsverfahren das digitale Signal mit einem kontinuierlichen Grundimpuls mit spezifischen Eigenschaften gefaltet, z. B. dem Raised-Cosine-Filter. Das Ergebnis ist dann ebenfalls ein analoges Signal.
Übertragung und Störungen
Ein digitales Signal ist weniger anfällig für Störungen bei der Übertragung, da die Signalpegel mit einer gewissen Toleranz immer noch dem korrekten Wert zugeordnet werden können. Jedes Signal wird bei der Übertragung immer durch Rauschen überlagert bzw. gestört. Wird das verrauschte Signal wieder digitalisiert, so verschwinden diese Störungen durch die Quantisierung wieder. Solange die Störungen nicht zu groß sind, erhält man so das ursprüngliche Signal wieder.
Deshalb sind digitale Signale besser geeignet, als analoge Signale, um über lange Strecken übertragen zu werden. Stellt man entlang der Strecke Repeater bereit, die das Signal aufbereiten, d. h. digitalisieren (ggf. Fehler korrigieren) und anschließend (wieder analog) weitersenden, so entfernt man dabei jedes Mal das unerwünschte Rauschen und sendet nur das Nutzsignal weiter. Ein rein analoges Signal kann zwar ebenfalls immer wieder verstärkt werden, allerdings verstärkt man hier auch bei jedem Mal das Rauschen mit.[2]
Dadurch ist es möglich, digitale Signale verlustfrei zu übertragen und digital übertragene oder gespeicherte Signale beliebig oft – und ohne Qualitätseinbußen – wieder zu kopieren.
Am Ende der Informationsverarbeitungskette ist zur Mitteilung an den Menschen in der Regel wieder eine Umsetzung in ein Analogsignal erforderlich, z. B. von der Audio-CD in elektrische Spannung und Schalldruck.
Abgrenzung zu anderen wertediskreten Signalen
Ein digitales Signal muss sowohl zeit- als auch wertediskret sein. Im Sinne der Schaltungstechnik ist die Eigenschaft der Zeitdiskretheit auch dann erfüllt, wenn sich das Signal nur zu diskreten Zeitpunkten ändern kann, dazwischen aber konstant und insoweit (zeit-)kontinuierlich vorhanden ist. Daneben existiert auch eine Reihe von wertediskreten Signalen, die jedoch keine digitalen Signale sind.
Zum Beispiel ist das ein pulsweitenmoduliertes Signal, das aus einem Rechtecksignal fester Frequenz besteht mit kontinuierlich variablem Tastgrad. Ebenfalls ist eine Folge von Rechteckimpulsen, wie sie bei Messung der Drehzahl mit einer Lichtschranke entsteht, kein Digitalsignal. Dieses Signal ist zwar wertediskret, sogar binär, aber es kann seinen Wert ohne Bindung an einen Zeittakt mit der Frequenz der Impulse ändern. Ein weiteres Beispiel für die zwar umgangssprachlich gebräuchliche, aber nicht korrekte Begriffsverwendung ist die Bezeichnung „Digitalverstärker“ für Klasse-D-Verstärker, welche mittels Pulsweitenmodulation arbeiten.[3]
Bedeutung
Aufgrund der sog. digitalen Revolution hat die Nutzung digitaler Signale drastisch zugenommen. Mittlerweile basieren die meisten Haushaltsgeräte entweder vollständig oder zumindest in großen Teilen auf Digitalsignalen. Kommunikationssysteme wie das Internet und die Mobiltelefonie basieren auf einem digitalen Signalnetz. Die Vorteile gegenüber analoger Technik sind vielseitigere Bearbeitungsmöglichkeiten und die fehlerfreie Speicherfähigkeit über lange Zeit, beispielsweise auf CD-ROMs.
Siehe auch
Literatur
- Karl-Dirk Kammeyer, Kristian Kroschel: Digitale Signalverarbeitung. 6. Auflage. Teubner, 2006, ISBN 3-8351-0072-6.
- Martin Werner: Signale und Systeme. 3. Auflage. Vieweg+Teubner, 2008, ISBN 978-3-8348-0233-0.
- Rolf Unbehauen: Systemtheorie 1. 7. Auflage. Vieweg+Teubner, 1997, ISBN 3-486-24022-6, S. 3 f.
- Dietmar Lochmann: Digitale Nachrichtentechnik. 3. Auflage. Verlag Technik, 2002, ISBN 978-3-341-01321-2, S. 25 f.
Einzelnachweise
- Martin Werner: Signale und Systeme. 3. Auflage. Vieweg+Teubner, 2008, ISBN 978-3-8348-0233-0, S. 3 bis 9.
- Dietmar Lochmann: Digitale Nachrichtentechnik. 3. Auflage. Verlag Technik, 2002, ISBN 978-3-341-01321-2, S. 26.
- Comparison of feedback implementations for digital audio amplifiers Artikel auf Audio DesignLine