Membranpotential

Das Membranpotential (präziser: die Transmembranspannung) ist eine spezielle elektrische Spannung zwischen zwei Flüssigkeitsräumen, in denen geladene Teilchen (Ionen) in unterschiedlichen Konzentrationen vorliegen. Ein Membranpotential entsteht, wenn die Flüssigkeitsräume durch eine Membran getrennt sind, die mindestens eine dieser Teilchensorten durchlässt, aber nicht von allen Teilchensorten gleich gut passiert werden kann (Semipermeabilität). Angetrieben durch zufällige Teilchenbewegung wechseln dann mehr Ionen einer Sorte auf die Seite niedrigerer Konzentration als in die umgekehrte Richtung (Diffusion), sodass eine Ladungstrennung und damit die Transmembranspannung resultiert. Die Ladungstrennung bedeutet gleichzeitig eine zunehmende elektrische Abstoßungskraft auf nachfolgende Teilchen, die schließlich genauso stark wird wie die Diffusion. In diesem Gleichgewichtszustand bewegen sich immer noch Teilchen der betrachteten Sorte über die Membran, aber in jedem Moment gleich viele in beide Richtungen; der Nettostrom ist null und das Membranpotential stabil. Stabile Membranpotentiale gibt es auch, wenn mehrere Teilchensorten beteiligt sind; in diesem Fall ist der Nettostrom für jede einzelne Teilchensorte fast immer ungleich null, der Nettostrom über alle Teilchen gerechnet dagegen ebenfalls null.

Membranpotentiale sind in der Biologie von überragender Bedeutung; alle lebenden Zellen bauen ein Membranpotential auf. Zur Herstellung und Aufrechterhaltung der Konzentrationsunterschiede benutzen sie dabei molekulare Pumpen wie die Natrium-Kalium-ATPase, selektive Permeabilität entsteht durch spezifische Ionenkanäle. Das Membranpotential nutzen Zellen für Transporte über die Membran; zeitlich veränderliche Membranpotentiale koordinieren die Herzaktion und leiten und integrieren Informationen in Gehirn und Nerven.

Physikalische Formulierung

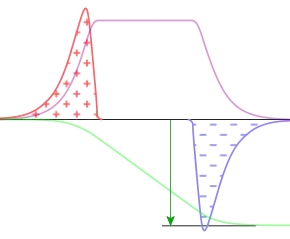
Verlauf elektrischer Größen quer durch eine Membran und angrenzende Elektrolyte. Das Bild ändert sich nicht prinzipiell, wenn Ladungen berücksichtigt werden, die an der Membranoberfläche gebunden sind.

Ein Membranpotential ist die elektrische Spannung über eine elektrochemische Doppelschicht, die aus einer Membran und Raumladungen in angrenzenden Elektrolyten besteht. In nebenstehendem Diagramm stehen die rote und die blaue Fläche für die positiven bzw. negativen Überschussladungen. Die einhüllenden Kurven stellen die Ladungsdichte dar. Diese fällt zur Mitte hin steil ab; dort ist der hydrophobe Teil der Membran, den Ladungen mit Hydrathülle meiden. Nach außen hin fällt die Ladungsdichte exponentiell ab. Das gilt auch für die elektrische Feldstärke (lila Kurve, i. W. das Wegintegral der Ladungsdichte), die abseits der Membran, falls dort kein Strom fließt, ganz verschwindet, sodass das elektrische Potential (grüne Kurve, Wegintegral der Feldstärke) dort jeweils konstant ist. Die Potentialdifferenz (Spannung) zwischen diesen konstanten Werten (grüner Pfeil) wird als Membranpotential bezeichnet, auch als Transmembranpotential oder gar elektrischer Gradient, worunter Physiker die Feldstärke verständen.

Ein Membranpotential kann wie bei einem Kondensator durch von außen zugeführte Ladung entstehen, etwa in den myelinisierten Abschnitten von Nervenfasern. Im biologischen Kontext bedeutender ist dagegen die Bildung des Membranpotentials durch Konzentrationsunterschiede auf beiden Seiten der Membran in Verbindung mit ionenselektiver Durchlässigkeit, gesteuerter Durchlässigkeit und aktivem Transport von Ionen durch die Membran.

Bei ausgedehnten Zellen, wie Nerven- oder Muskelzellen, variiert das Membranpotential räumlich. Es dient dort der Signalleitung bzw. -ausbreitung, in Sinneszellen und dem Zentralnervensystem auch der Informationsverarbeitung. In Chloroplasten und Mitochondrien dient das Membranpotential der energetischen Kopplung von Prozessen des Energiestoffwechsels: Ein Prozess, siehe Elektronentransportkette, transportiert Ionen gegen die Spannung und leistet dabei Arbeit, ein anderer, siehe ATP-Synthase, wird von der Potentialdifferenz angetrieben.

Messung

Messen des Membranpotentials einer Oocyte von Xenopus laevis durch eingestochene Mikroelektrode.

Da sich das Potential auf beiden Seiten der Membran (fehlende Ströme vorausgesetzt) schon nach geringem Abstand zur Membran kaum noch ändert, genügt zur Messung der Transmembranspannung jeweils eine Elektrode irgendwo in den beiden Elektrolytlösungen. Die physiologische Vorzeichenkonvention lautet allgemein „Innen- minus Außenpotential“. Für die Messung des Plasmamembranpotentials bedeutet dies, dass eine der beiden Elektroden ins Zytosol eingeführt werden muss, das gemessene Membranpotential lässt sich dann auch als das Potential des Zytosols bei Wahl der extrazellulären Flüssigkeit als Bezugspunkt interpretieren.

Die Messung von Membranpotentialen an mikroskopischen Strukturen, möglichst ohne elektrische, chemische und mechanische Beeinflussung, ist schwierig. Das Foto zeigt die Ableitung des Innenpotentials einer Zelle mit einer feinen Glaskapillare. An der Öffnung der Kapillare entsteht ein kleines Diffusionspotential, denn sie ist mit einem starken Elektrolyten in hoher Konzentration gefüllt, z. B. 3 M KCl, um einen definierten Übergang auf den metallischen Leiter zu gewährleisten, der sich in der Kapillare befindet und am Bildrand zu sehen ist. Die für die Messung des Membranpotentials notwendige Erfassung auch des Außenpotentials ist nicht mit im Bild.

Physiologische Werte

Die Phospholipid-Doppelschicht der Einheitsmembran hat einen hydrophoben Kern, der die Raumladungen gut fünf nm auseinanderhält. Das Ruhepotential tierischer Zellen liegt bei −70 mV. Daraus resultiert eine Feldstärke von über 10⁷ V/m oder etwa das Vierfache der Durchschlagsfestigkeit von Luft. Bei Spannungen von 0,7 bis 1,1 Volt tritt Elektroporation ein.

Aus den Faktoren Feldstärke, Permittivitätszahl des Membranmaterials (≥ 2) und elektrische Feldkonstante ergibt sich eine Flächenladungsdichte von knapp 3·10⁻⁴ C/m², was sich mit der Faraday-Konstante in 3·10⁻⁶ mval/m² übersetzt.

Die für den exponentiellen Abfall der Raumladungsdichte charakteristische Debye-Länge beträgt unter physiologischen Bedingungen knapp einen Nanometer. In dieser Schicht befinden sich positive und negative bewegliche Ladungsträger in einer Flächenkonzentration von etwa 2·10⁻⁴ mval/m². Die Nettoladung macht also nur etwa 1 % der Ladungsdichte aus.

Potentialänderungen als Signale

Nervenzellen codieren Information in Gestalt von kurzfristigen Potentialänderungen. Diese lassen sich in zwei Gruppen unterteilen, die unterschiedliche Eigenschaften und Funktionen haben:

graduierte Potentiale treten als Rezeptorpotential bei Sinneszellen auf und als postsynaptisches Potential bei chemischen Synapsen und der motorischen Endplatte.
Aktionspotentiale werden am Axonhügel und am Axon einer Nervenzelle oder an der subsynaptischen Membran von Muskelzellen erzeugt.

Vergleich in der Übersicht:

	graduiertes Potential	Aktionspotential
1	amplitudenmoduliert	frequenzmoduliert
2	graduierte Amplitude	konstante Amplitude
3	nicht refraktär	refraktär
4	Summation möglich	keine Summation möglich („Alles-oder-Nichts-Prinzip“)
5	Ausbreitung passiv mit Amplitudenabfall	Ausbreitung aktiv mit Erhalt der Amplitude
6	keine Auslöseschwelle	definierte Auslöseschwelle
7	Depolarisation oder Hyperpolarisation mit anschließender Repolarisation	nur Depolarisation mit anschließender Repolarisation
8	unspezifische Kationenkanäle	schnelle, spannungsgesteuerte Natrium-Ionenkanäle
9	Dauer 40 bis 4000 ms	Dauer 4 ms

Grundlagen der Entstehung

Diffusion

Gelöste Teilchen befinden sich als Ausdruck ihrer thermischen Energie in ständiger Bewegung. Diese Bewegung heißt brownsche Molekularbewegung und ist völlig ungerichtet. Wenn zwischen zwei Orten, die sich in der Konzentration einer Teilchensorte unterschieden, eine für diese Teilchensorte passierbare Verbindung besteht, bewegen sich netto Teilchen in Richtung der niedrigeren Konzentration, bis schließlich gleiche Konzentrationen erreicht sind. Dieser Prozess heißt Diffusion; er wird nicht durch eine Kraft angetrieben, sondern ergibt sich allein aus der zufälligen Bewegung. Ein einzelnes Teilchen kann sich auch in die andere Richtung bewegen; bei einer großen Zahl von Teilchen ergibt sich aber stets ein Konzentrationsausgleich, weil dies wahrscheinlich oder anders gesagt thermodynamisch günstig ist.

Gleichgewichtspotential

Wenn geladene Teilchen (Ionen) diffundieren, verkompliziert sich die Situation, weil mit der Diffusion eine Ladungstrennung verbunden ist. Diese erzeugt eine zunehmende elektrostatische Kraft, die die Ionen in Richtung der höheren Konzentration beschleunigt, sodass ihre Bewegung nicht mehr völlig ungerichtet ist und sich damit auch kein völliger Konzentrationsausgleich mehr ergeben kann. Aber auch hier stellt sich irgendwann ein Gleichgewicht (ein Zustand ohne Nettostrom) ein, nämlich dann, wenn sich der elektrische und der stochastische Antrieb genau gegenseitig aufheben. Die elektrische Spannung, bei der dies der Fall ist, heißt Gleichgewichtspotential und lässt sich mit der Nernst-Gleichung berechnen.

Modellversuch

Eine mit Kochsalzlösung gefüllte Kammer wird durch eine selektive, semipermeable Membran, die nur das Kation Natrium passieren lässt, in zwei Halbzellen unterteilt. In jeder Halbzelle befindet sich eine Elektrode; die beiden Elektroden sind durch ein Spannungsmessgerät miteinander verbunden, das zu diesem Zeitpunkt null anzeigt. Wird in einer der beiden Halbzellen (zum Beispiel der rechten) weiteres Kochsalz aufgelöst, beobachtet man zunächst einen Anstieg der Spannung, die dann als „Gleichgewichtsspannung“ erhalten bleibt.

Erklärung

Aufgrund des Konzentrationsgefälles diffundieren Natrium-Ionen durch die Membran. Aufgrund der Ladungstrennung baut sich ein Potentialgefälle auf: Die Innenseite der Membran (linke Kammer) wird positiv, die Außenseite (rechte Kammer) negativ. Durch das sich aufbauende Potentialgefälle wird die Diffusionsgeschwindigkeit immer geringer. Das Diffusionsgleichgewicht ist dann erreicht, wenn die treibende „Kraft“ des Konzentrationsgefälles für die Diffusion nach links genauso groß ist wie die treibende Kraft des Potentialgefälles für die Diffusion nach rechts. Die bis dahin netto geflossene Ladung ist so gering, dass sich die Konzentrationen in den beiden Halbzellen nicht wesentlich verändert haben.

Allgemeines Membranpotential

Ist eine Membran für mehrere Ionen durchlässig, für die sich die Gleichgewichtspotentiale unterscheiden, ist bei den gegebenen Konzentrationen kein thermodynamisches Gleichgewicht möglich. Dennoch stellt sich auch hier ein temporär stabiler Zustand ein: das Nullstrompotential. Bei dieser Spannung bestehen zwar für einzelne Ionensorten Nettoströme, alle Ströme zusammen addieren sich jedoch zu null. Das Membranpotential liegt dabei umso näher am Gleichgewichtspotential einer Ionensorte, je höher die Permeabilität für diese Ionensorte ist; der genaue Wert kann mithilfe der Goldman-Gleichung berechnet werden.

Konstanthaltung der Konzentrationen

Die Ionenströme im Fall des allgemeinen Membranpotentials würden langfristig die Konzentrationsunterschiede abbauen, sodass sich die Spannung ändern und schließlich null erreichen würde. Für ein konstantes Membranpotential ist somit ein Mechanismus notwendig, der die Ionen entgegen der Richtung der passiven Ströme wieder zurück transportiert. Dieser Transport ist aktiv, d. h., er benötigt Gibbs-Energie. In biologischen Systemen kommt der Natrium-Kalium-Pumpe eine große Bedeutung zu. Sie schafft drei Natriumionen im Austausch gegen zwei Kaliumionen aus der Zelle, die Gibbs-Energie dazu stammt aus der Hydrolyse eines ATP in ADP und Phosphat. Über Kotransporter treibt die Natrium-Kalium-ATPase mittelbar weitere Ionenrücktransporte an, man spricht von sekundär oder tertiär aktivem Membrantransport.

Herleitung über freie Enthalpie

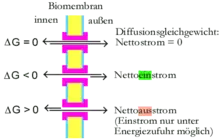
passiver Transport durch geöffnete Ionenkanäle

An der freien Enthalpie ΔG kann abgelesen werden, ob sich bei einem gegebenen Membranpotential und gegebenen Konzentrationsverhältnissen Teilchen netto über eine Membran bewegen:

Ist ΔG = 0, liegt ein thermodynamisches Gleichgewicht vor: Die Anzahl der pro Zeitspanne durch die Membran diffundierenden Teilchen ist in beide Richtungen gleich groß.
Ist ΔG < 0, ist der Transport exergon, läuft also in die betrachtete Richtung freiwillig ab.
Ist ΔG > 0, ist der Transport endergon, läuft also in die betrachtete Richtung nur dann ab, wenn er an einen exergonen Vorgang (wie die Hydrolyse von ATP) gekoppelt wird.

Die freie Enthalpie kann auch als Maß des elektrochemischen Potentials angesehen werden, das sich aus den beiden Komponenten

chemisches Potential (entspricht der Konzentrationsdifferenz) und
elektrisches Potential (entspricht der Potentialdifferenz) zusammensetzt.

Chemisches Potential – Vernachlässigung des Potentialunterschieds

Für den Transport von außen nach innen (Import) gilt die Formel

\Delta G=R\cdot T\cdot \ln {\frac {c(A_{i})}{c(A_{a})}}

.

Erläuterung:

R: Allgemeine Gaskonstante R = 8,3143 J·mol⁻¹·K⁻¹

T: Temperatur in Kelvin

c(A_i), c(A_a): Stoffmengen-Konzentrationen des Stoffes A innen, außen

ln: natürlicher Logarithmus

Für T = 298 K und Benutzung des dekadischen Logarithmus vereinfacht sich die Gleichung zu

\Delta G=5{,}7\,\mathrm {kJ/mol} \cdot \lg {\frac {c(A_{i})}{c(A_{a})}}

.

Wenn die Konzentration des Stoffes A innen genau so groß ist wie außen, ist ΔG = 0, es liegt Konzentrationsausgleich vor und es findet kein Stofftransport statt.
Ist die Konzentration innen größer als außen, ist ΔG > 0, es findet kein passiver („freiwilliger“) Stofftransport von außen nach innen statt.
Ist die Konzentration außen größer als innen, ist ΔG < 0, es findet Stofftransport von außen nach innen statt.

Elektrisches Potential – Vernachlässigung des Konzentrationsunterschieds

Die freie Enthalpie für den reinen Ladungstransport beträgt

\Delta G_{\text{Ladungstransport}}=Z\cdot F\cdot \Delta \Psi

.

Erläuterung:

Z: Die Ladungszahl Z entspricht der Ionenladung des zu transportierenden Teilchens. Sie ist für Kationen positiv, für Anionen negativ.

F: Faraday-Konstante F = 96485 C·mol⁻¹

ΔΨ: Membranpotential

Elektrochemisches Potential

Für den Import geladener Teilchen ergibt sich durch Addition

\Delta G=R\cdot T\cdot \ln {\frac {c(A_{i})}{c(A_{a})}}+Z\cdot F\cdot \Delta \Psi

.

Nernst-Gleichung

Für den Gleichgewichtsfall (ΔG = 0) lässt sich das Gleichgewichtspotential ΔΨ₀ für ein Ion durch Umstellung obiger Gleichung ermittelt:

\Delta \Psi _{0}=-{\frac {\mathrm {R} \cdot T}{Z\cdot F}}\cdot \ln {\frac {c(A_{i})}{c(A_{a})}}

für Z = 1 (bei Na⁺, K⁺) und T = 298 K ergibt sich bei Benutzung des dekadischen Logarithmus die vereinfachte Gleichung

\Delta \Psi _{0}=-59{,}1\,\mathrm {mV} \cdot \lg {\frac {c(A_{i})}{c(A_{a})}}

.

Goldman-Hodgkin-Katz-Gleichung

Die Goldman-Gleichung liefert das Nullstrompotential bei Betrachtung mehrerer Ionen, sie sei hier ohne Herleitung aufgeführt:

\Delta \Psi ={\frac {RT}{F}}\cdot \ln {\frac {\Sigma [P_{\mathrm {ka} }\cdot c_{\mathrm {ka-a} }]+\Sigma [P_{\mathrm {an} }\cdot c_{\mathrm {an-i} }]}{\Sigma [P_{\mathrm {ka} }\cdot c_{\mathrm {ka-i} }]+\Sigma [P_{\mathrm {an} }\cdot c_{\mathrm {an-a} }]}}

Erläuterung:

P: Permeabilität der Kanäle für Anionen (an) und Kationen (ka)

c: Konzentration der Anionen und Kationen innerhalb (-i) oder außerhalb (-a) der Zelle

Beispiel für ein Membranpotential (Mischpotential) ΔΨ von −53 mV bei 298 K:

Ionensorte	c_eq(A_außen)	c_eq(A_innen)	ΔΨ₀	ΔG für einen Transport von außen nach innen
Na⁺	400 mmol/l	20 mmol/l	+76 mV	+2,3 kJ/mol
K⁺	50 mmol/l	440 mmol/l	−55 mV	−10,5 kJ/mol
Cl⁻	108	560	+43 mV	−11,0 kJ/mol

Literatur

Jacob Kraicer, Samuel Jeffrey Dixon: Measurement and Manipulation of Intracellular Ions. Academic Press, 1995, ISBN 0-08-053646-8, eingeschränkte Vorschau in der Google-Buchsuche

Weblinks

Zellphysiologie

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.