Spannungsteiler

Der Spannungsteiler ist eine Reihenschaltung aus passiven elektrischen Zweipolen, durch die eine elektrische Spannung aufgeteilt wird.

In Bezug auf magnetische Kreise wird der Begriff Spannungsteiler auch verwendet, um die Aufteilung der magnetischen Spannung (Durchflutung) entlang von magnetischen Widerständen zu beschreiben.

Einfacher Spannungsteiler mit zwei ohmschen Widerständen

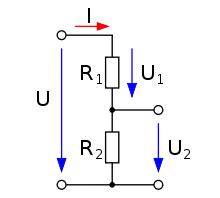
Spannungsteiler aus zwei in Reihe geschalteten ohmschen Widerständen

Der Spannungsteiler wird im Standardfall beschrieben durch die Reihenschaltung von zwei ohmschen Widerständen.

Zur Berechnung der Teilspannung U₂ über R₂ wird zunächst der Gesamtwiderstand nach der Regel für Reihenschaltungen wie folgt berechnet:

R_{\mathrm {ges} }=R_{1}+R_{2}\!\,

Die Gesamtspannung sowie die Werte der Widerstände sind im Allgemeinen bekannt, wodurch sich nach dem Ohmschen Gesetz der Strom I bestimmen lässt:

I={\frac {U}{R_{\mathrm {ges} }}}={\frac {U}{R_{1}+R_{2}}}

Nach den Regeln für Reihenschaltungen ist der Strom durch alle Bauteile identisch und somit ergibt sich das gesuchte U₂ zu:

U_{2}=I\cdot R_{2}

Wird die Formel für den gemeinsamen Strom hier eingesetzt, ergibt sich die Ausgangsspannung in Abhängigkeit von den Teilerwiderständen und der Eingangsspannung allgemein:

U_{2}={\frac {U}{R_{\mathrm {ges} }}}\cdot R_{2}

Durch Äquivalenzumformung weiter verallgemeinert folgt das Verhältnis zwischen Ein- und Ausgangsspannung in Abhängigkeit von den Teilerwiderständen.

U_{2}={\frac {U}{R_{1}+R_{2}}}\cdot R_{2}=U\cdot {\frac {R_{2}}{R_{1}+R_{2}}}\quad \Leftrightarrow \quad {\frac {U_{2}}{U}}={\frac {R_{2}}{R_{1}+R_{2}}}

An diesem umgeformten Ausdruck ist erkennbar, dass das Verhältnis von dem Spannungsabfall $U_{2}$ über $R_{2}$ zu der Gesamtspannung $U$ identisch ist mit dem Verhältnis von Widerstand $R_{2}$ zu dem Gesamtwiderstand aus $R_{1}$ und $R_{2}$ .

Durch weitere Äquivalenzumformungen entstehen folgende praktische Gleichungen:

{\frac {R_{1}}{U_{1}}}={\frac {R_{2}}{U_{2}}}

beziehungsweise:

{\frac {U_{1}}{R_{1}}}={\frac {U_{2}}{R_{2}}}

Diese Gleichungen werden oft bei der Dimensionierung (dem Auswählen geeigneter Widerstände im Hinblick auf die Verlustleistung, der Höhe der Ausgangsspannung und folglich auch der Höhe des Last- und Querstromes) des Spannungsteilers eingesetzt.

Spannungsteilerregel

Mit Hilfe der Spannungsteilerregel können Teilspannungen direkt aus den Teilwiderständen und der Gesamtspannung berechnet werden. Die letzte Gleichung für die vorangegangene Schaltung stellt den Spezialfall der Spannungsteilerregel für genau zwei Teilwiderstände dar. Die Spannungsteilerregel ist nur anwendbar, wenn alle Bauelemente, auf die sich die Gesamtspannung aufteilt, linear und passiv sind. Sobald aktive Bauelemente wie Quellen vorkommen, muss auf das Knotenpotentialverfahren oder Maschenstromverfahren zurückgegriffen werden.

Verbal lautet die Spannungsteilerregel:

{\frac {\text{Teilspannung}}{\text{Gesamtspannung}}}={\frac {\text{Widerstand unter Teilspannungsabfall}}{\text{Gesamtwiderstand}}}

Verallgemeinert auf n in Reihe geschaltete Widerstände (i = 1, …, n) ergeben sich für die Teilspannung über den Widerstand k die nachfolgenden Gleichungen für die jeweiligen Anwendungsfälle (mit n und k ganzzahlig, n ≥ 1, 1 ≤ k ≤ n). Widerstände in Parallelschaltungen müssen zunächst zu einem Widerstand zusammengefasst werden, um den Gleichungen in der dargestellten Form zu entsprechen. Der Gesamtwiderstand bezieht sich nur auf die Widerstände, über die die Gesamtspannung abfällt. Eventuelle Widerstände, die vor, nach oder in parallelen Zweigen zum betrachteten Abschnitt liegen, werden nicht berücksichtigt. Bei Schaltungen mit inneren parallelen Verzweigungen muss die Formel eventuell mehrmals angewendet werden, um die gesuchte Teilspannung zu erhalten.

Gleichspannungsfall

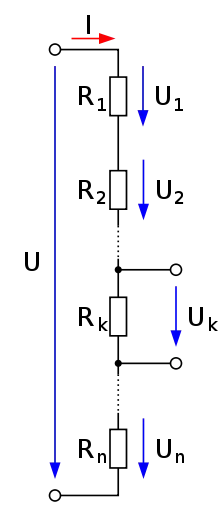
Spannungsteiler mit ohmschen Widerständen

Bei Gleichspannung treten nur reellwertige Widerstandswerte, sogenannte ohmsche Widerstände auf.

{\frac {U_{k}}{U}}={\frac {R_{k}}{R}}

mit dem Gesamtwiderstand

R=\sum _{i=1}^{n}R_{i}

Bei Gleichspannung sind die einzelnen Teilspannungen immer kleiner als die Gesamtspannung. Das Verhältnis von Teilspannung zur Gesamtspannung nimmt Werte zwischen 0 und 1 an. Typisches Beispiel eines einstellbaren Spannungsteiler ist ein Potentiometer, bei dem über einen verschiebbaren Kontakt auf einem durchgehenden Widerstandskörper das Teilungsverhältnis variabel eingestellt werden kann. Teilspannungen verhalten sich proportional zu den Widerständen, über die sie abfallen. Das bedeutet, je kleiner (größer) der Widerstand ist, desto kleiner (größer) ist die Teilspannung.

Wechselspannungsfall

Bei harmonischer Wechselspannung mit einer konstanten Kreisfrequenz ω können zusätzlich komplexe Widerstände, sogenannte Impedanzen, in Form von Kapazitäten (kapazitiver Spannungsteiler) und Induktivitäten (induktiver Spannungsteiler) auftreten. Die Berechnung eines Spannungsteilers ist dann ein Teil der komplexen Wechselstromrechnung.

{\frac {U_{k}}{U}}={\frac {Z_{k}}{Z}}

mit der Gesamtimpedanz

Z=\sum _{i=1}^{n}Z_{i}

Bei Wechselspannung und den auftretenden Impedanzen können durch die Energiespeicherung in den Impedanzen die Teilspannungen an den Kapazitäten und Induktivitäten durch Resonanz größer als die Gesamtspannung werden. Wichtig ist bei der Anwendung der Spannungsteilerregel mit Wechselspannung, dass die Impedanzen, insbesondere Induktivitäten, untereinander über ihre im elektrischen bzw. magnetischen Feld gespeicherte Energie nicht gekoppelt sind. Dieser Umstand ist gleichbedeutend mit der Forderung von passiven Zweipolen, welche keine Spannungs- oder Stromquellen aufweisen.

Magnetische Kreise

In magnetischen Kreisen teilt sich die magnetische Spannung nur auf magnetische Widerstände auf.

{\frac {U_{m_{k}}}{U_{m}}}={\frac {R_{m_{k}}}{R_{m}}}

mit dem Gesamtwiderstand

R_{m}=\sum _{i=1}^{n}R_{m_{i}}

Beispiele

Beispiel mit mehrfacher Anwendung

Spannungsteiler mit einer inneren Verzweigung

Gesucht wird die Spannung über $R_{21}$ in der nebenstehenden Schaltung. Aufgrund der verschachtelten Lage des Widerstandes ist eine mehrfache Anwendung der Spannungsteilerregel notwendig. Dazu wird zunächst die Spannung $U_{2}$ über der Parallelschaltung berechnet. Die Spannungsteilerregel ergibt die Gleichung:

{\frac {U_{2}}{U}}={\frac {R_{2}}{R_{1}+R_{2}}}

mit $\,R_{2}=\left(R_{21}+R_{22}\right)\parallel R_{23}$

Die Teilspannung $U_{2}$ teilt sich auf die Reihenschaltung aus $R_{21}$ und $R_{22}$ auf. Durch nochmalige Anwendung der Spannungsteilerregel, wird die Spannung über $R_{21}$ abhängig von $U_{2}$ ermittelt:

{\frac {U_{21}}{U_{2}}}={\frac {R_{21}}{R_{21}+R_{22}}}

Werden beide Gleichungen miteinander multipliziert, ergibt sich eine Gesamtgleichung in der $U_{21}$ direkt von U abhängig ist:

{\frac {U_{2}}{U}}\cdot {\frac {U_{21}}{U_{2}}}={\frac {U_{21}}{U}}={\frac {R_{2}}{R_{1}+R_{2}}}\cdot {\frac {R_{21}}{R_{21}+R_{22}}}

Beispiel für magnetischen Kreis

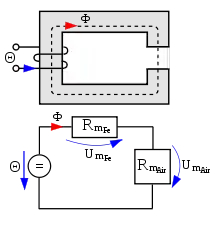
magnetischer Spannungsteiler aus zwei Widerständen

In magnetischen Kreisen wird die Regel genauso angewendet. Für die Teilspannungen über $R_{m_{\text{Fe}}}$ und $R_{m_{\text{Air}}}$ ergeben sich die Gleichungen:

{\frac {U_{m_{\text{Fe}}}}{\Theta }}={\frac {R_{m_{\text{Fe}}}}{R_{m}}}

bzw. für den anderen Zweig

{\frac {U_{m_{\text{Air}}}}{\Theta }}={\frac {R_{m_{\text{Air}}}}{R_{m}}}

mit dem Gesamtwiderstand:

R_{m}=R_{m_{\text{Fe}}}+R_{m_{\text{Air}}}

Belasteter Spannungsteiler

Belasteter Spannungsteiler mit Lastwiderstand R_L parallel zu R₂

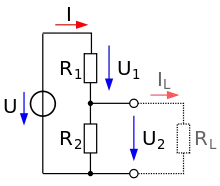
In der Schaltung im Abschnitt Einfacher Spannungsteiler mit zwei ohmschen Widerständen sei an den Anschlüssen von R₂ der Ausgang. Wird dort ein Verbraucher mit dem Widerstand $R_{L}$ parallel zu R₂ angeschlossen, entsteht ein belasteter Spannungsteiler, für den die Spannungsberechnungen neu durchgeführt werden müssen. Der Widerstand der Parallelschaltung $R_{P}$ aus $R_{2}$ und $R_{L}$ ist kleiner als der kleinste Teilwiderstand der Parallelschaltung. Er wird berechnet mit:

R_{P}=R_{2}\parallel R_{L}={\frac {R_{2}\cdot R_{L}}{R_{2}+R_{L}}}

Infolge der Verringerung des Widerstands sinkt nach der Spannungsteilerregel die Spannung $U_{2}$ proportional dazu. Sie ergibt sich nun zu:

U_{2}={\frac {R_{P}}{R_{1}+R_{P}}}\cdot U

Ersatzspannungsquelle bzw. Thévenin-Äquivalent

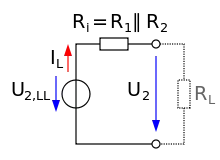
Zur Verdeutlichung des Einflusses des Lastwiderstandes kann die ursprüngliche Schaltung ohne R_L in eine Zweipolersatzschaltung mit einer Ersatzspannungsquelle U_2,LL und einem Innenwiderstand R_i umgerechnet werden. Nach den Regeln zur Berechnung von Ersatzschaltungen für aktive Zweipole ergeben sich für dieses Beispiel die folgenden Gleichungen:

U_{2,LL}=U\cdot {\frac {R_{2}}{R_{1}+R_{2}}}

R_{i}=R_{1}\|R_{2}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}={\frac {R_{1}\cdot R_{2}}{R_{1}+R_{2}}}

Der Lastwiderstand bleibt von der Umstellung unbeeinflusst und seine Wirkung auf die Ausgangsspannung des Spannungsteilers tritt deutlich hervor. Es entsteht nun ein einfacherer Spannungsteiler aus R_i und R_L.

U_{2}=U_{2,LL}\cdot {\frac {R_{L}}{R_{i}+R_{L}}}

Mit Hilfe von R_i lässt sich eine Empfehlung zur geeigneten Wahl der Widerstände ausdrücken. Damit der Lastwiderstand einen geringen Einfluss auf die Ausgangsspannung hat, sollte der Innenwiderstand einen deutlich kleineren Wert als die Last aufweisen.

R_{i}\ll R_{L}\quad \Rightarrow \quad R_{i}<{\frac {1}{10}}\cdot R_{L}

Anwendung

Die Anwendungsbeispiele überschneiden sich mit den Anwendungen von Potentiometern (einstellbare Spannungsteiler). Spannungsteiler werden verwendet:

zur Pegelanpassung
in Dämpfungsgliedern, z. B. auch zur Lautstärkeregelung
zur Spannungsmessung; Vielfachmessgeräte besitzen einen umschaltbaren Spannungsteiler für die Messung in verschiedenen Bereichen.
in Messspitzen für Oszilloskope: hier sind meist Spannungsteiler mit Teilerverhältnissen von 10 zu 1 oder 100 zu 1 zu finden. Diese Messspitzen (engl. probes) besitzen zusätzlich zum Widerstands-Spannungsteiler eine Frequenzkompensation, die die Leitungs- und Eingangskapazität bei Wechselspannungsmessungen ausgleicht. Die Kompensation ist oft einstell- bzw. abgleichbar. Sie stellt einen parallel liegenden kapazitiven Spannungsteiler dar.
zur Hochspannungsmessung (Hochspannungs-Messspitzen bzw. -tastköpfe); Teilerverhältnisse von 1000:1 oder größer. Eingangsspannungen bis etwa 40 kV sind gängig. Der obere Teilwiderstand beträgt ca. 1…100 GΩ, oft ist der Eingangswiderstand des Messgerätes (z. B. 1 oder 10 MΩ) berücksichtigt. Hochspannungs-Messspitzen gibt es unkompensiert für Gleichspannungsmessungen, aber auch frequenzkompensiert für Wechselspannungsmessungen.
induktive und resistive Spannungsteiler werden zur Positions- und Winkelbestimmung sowie in Beschleunigungsaufnehmern verwendet. Die hierbei eingesetzten induktiven Spannungsteiler arbeiten ohne Kontakte mit einem verschiebbaren weichmagnetischen Kern wie ein doppeltes Variometer.
induktive Spannungsteiler liefern in der Messtechnik hochpräzise Spannungsverhältnisse, die fast ausschließlich vom Windungszahlenverhältnis des verwendeten Transformators abhängig sind. Induktive Spannungsteiler sind sowohl mit festen Spannungsverhältnissen als auch als einstellbare Dekaden im Einsatz.
zur Erstellung einer Brückenschaltung durch Kombinierung von Spannungsteilern.
Eine spezielle Bauform mit fixen Widerständen und Stufenschalter zur Umschaltung stellt der Kelvin-Varley-Spannungsteiler dar. Er erlaubt die wiederholbare Einstellung der Teilerwerte des Spannungsverhältnisses.

Siehe auch

Literatur

Reinhold Pregla: Grundlagen der Elektrotechnik. 7. Auflage. Hüthig Verlag, Heidelberg 2004, ISBN 3-7785-2867-X.
Klaus Lunze: Einführung in die Elektrotechnik. 13. Auflage. Verlag Technik, Berlin 1991, ISBN 3-341-00980-9.
Heinz Meister: Elektrotechnische Grundlagen. 9. Auflage. Vogel Fachbuchverlag, Würzburg 1991, ISBN 3-8023-0528-0.

Weblinks

Wikibooks: Spannungsteiler – Lern- und Lehrmaterialien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.