Resonanz

Resonanz (von lateinisch resonare „widerhallen“) ist in Physik und Technik das verstärkte Mitschwingen eines schwingfähigen Systems, wenn es einer zeitlich veränderlichen Einwirkung unterliegt. Dabei kann das System um ein Vielfaches stärker ausschlagen als beim konstanten Einwirken der Anregung mit ihrer maximalen Stärke. Bei periodischer Anregung muss die Anregungsfrequenz oder ein ganzzahliges Vielfaches davon in der Nähe einer Resonanzfrequenz des Systems liegen. Das Phänomen kann bei allen schwingfähigen physikalischen und technischen Systemen auftreten und kommt auch im Alltag häufig vor. Resonanzen werden in der Technik oft ausgenutzt, um eine bestimmte Frequenz herauszufiltern oder zu verstärken. Wo eine Verstärkung nicht gewünscht ist, müssen unerwünschte Resonanzen jedoch vermieden werden.

Die im Resonanzfall anwachsenden Ausschläge entstehen dadurch, dass das System bei jeder Schwingung erneut Energie aufnimmt und speichert. Um zu verhindern, dass das System durch zu große Ausschläge aus dem schwingfähigen Amplitudenbereich austritt (Resonanzkatastrophe) oder zerstört wird, kann seine Dämpfung erhöht, seine Eigenfrequenz oder die Anregungsfrequenz verändert, oder die Stärke der Anregung verringert werden. Das anfängliche Anwachsen der Ausschläge wird dadurch begrenzt, dass die zugeführte Energie zunehmend von der Dämpfung (z. B. Reibung) aufgezehrt wird, oder dadurch, dass sich bei zu großem Unterschied zwischen Resonanz- und Anregungsfrequenz der Energiefluss immer wieder umkehrt, weil Anregung und schwingendes System „aus dem Takt“ geraten.

Als Folge stellt sich im Laufe der Zeit der Zustand der eingeschwungenen Schwingung her, bei dem die Amplitude konstant bleibt und die Schwingungsfrequenz mit der Anregungsfrequenz übereinstimmt. Die weiterhin in jeder Schwingung zugeführte Energie wird dann vollständig von der Dämpfung aufgezehrt. Nach Abschalten der Anregung kommt das System in Form einer gedämpften Schwingung mit seiner Eigenfrequenz allmählich zur Ruhe.

Das Phänomen der Resonanz spielt in Physik und Technik auf vielen Gebieten eine wichtige Rolle, zum Beispiel in der Mechanik, Akustik, Baudynamik, Elektrizitätslehre, Geowissenschaft, Astronomie, Optik und Quantenphysik. In der modernen Quantenphysik gilt die Gleichung $E=hf$ , die jedem Energiebetrag $E$ vermittels der Planckschen Konstante $h$ die Frequenz $f$ einer Schwingung zuordnet. Anstelle der Resonanz bei einer bestimmten Frequenz betrachtet man hier die Resonanz bei einer bestimmten Energie, die der Differenz der Energien von zwei verschiedenen Anregungszuständen des betrachteten Systems entspricht.

Geschichte

Der Begriff Resonanz stammt aus der Akustik, wo er von altersher das deutlich bemerkbare Mitschwingen von Saiten bei Tönen geeigneter Tonhöhe bezeichnet. Die Anregung großer Schwingungen durch periodisch wirkende Kräfte der richtigen Frequenz wurde schon in Galileis Untersuchungen 1602 und 1638 zu Pendeln und Saiten beschrieben, die am Beginn der neuzeitlichen Naturwissenschaft standen. Allerdings nahm er auch an, Schwingungen mit anderer als der Eigenfrequenz ließen sich überhaupt nicht anregen.[1][2] Eine entsprechende Bewegungsgleichung für einen Massenpunkt (ohne Dämpfung der Bewegung) wurde 1739 von Leonhard Euler erstmals aufgestellt. Seine allgemeine Lösung enthielt bereits das Mitschwingen mit der Frequenz der anregenden Kraft in Überlagerung mit einer Schwingung mit der Eigenfrequenz, sowie im Falle der Gleichheit beider Frequenzen das unbegrenzte Anwachsen der Schwingungsweite. Er sah diese Ergebnisse, die sich aus der Rechnung ergaben, allerdings als „wunderliche“ theoretische Voraussage an.[3] 1823 behandelte Thomas Young im Zusammenhang mit den Gezeiten die mechanische Resonanz einschließlich Dämpfung und gab erstmals die vollständige Berechnung von Resonanzkurve und Phasenverschiebung an.[4] Im Zusammenhang mit der Erzeugung und dem Nachweis elektrischer und magnetischer Schwingungen fand Anton Oberbeck für den elektrischen Schwingkreis dieselben Erscheinungen, worauf er die Bedeutung des Begriffs „Resonanz“ entsprechend erweiterte.[5] Die Entdeckung der elektromagnetischen Wellen durch Heinrich Hertz, sowie deren Nutzung zur drahtlosen Telegraphie durch Guglielmo Marconi ab 1895, verschafften der elektromagnetischen Resonanz dann schnell eine große Bedeutung in Wissenschaft und Technik.

Jedoch wurde die mechanische Resonanz im Wesentlichen erst ab Anfang des 20. Jahrhunderts richtig gewürdigt, nachdem der Physiker und Mathematiker Arnold Sommerfeld – als erster Professor für Technische Mechanik, der nicht vorher Ingenieur gewesen war – darauf hingewiesen hatte. Damals waren Hängebrücken mit marschierenden Soldaten oder schnell fahrenden Dampflokomotiven schon durch Resonanz eingestürzt, und bei den langen Antriebswellen von größeren Dampfschiffen waren bei bestimmten Geschwindigkeiten bereits unerwartet starke Schwingungen aufgetreten, die mehrfach schon zu Zerstörungen geführt hatten.[6][7][8][9][10]

Alltagsbeispiele

Resonanz kommt im Alltag häufig vor. Allerdings sind nicht alle Schwingungen Folge einer Resonanz.

Beim wiederholten Anschwingen einer Kinderschaukel gibt man der Schaukel immer dann einen Schubs, wenn diese nach vorne schwingt. Die Anregungsstöße erfolgen dabei periodisch und offensichtlich gerade mit der Frequenz der Schaukelschwingung: es handelt sich also um Resonanz. Man beachte, dass die Krafteinwirkung bei den anregenden Schubsen keineswegs wie eine Sinuskurve verläuft, es reicht aus, dass sie periodisch erfolgt. Dabei kann die Anregungsfrequenz auch einen ganzzahligen Bruchteil der Schwingungsfrequenz betragen, wenn man z. B. nur jedes zweite oder dritte Mal anschubst.

Anders ist das bei einem ruhenden Pendel, wenn man ihm einen einmaligen Stoß gibt. Auch wenn das Ergebnis ähnlich ist, nämlich dass das Pendel nun schwingt, so liegt keine periodische Anregung vor und es handelt sich nicht um Resonanz.

Jeder kennt die Situation in der Kantine: man trägt einen Teller Suppe auf dem Tablett. Stimmt die Frequenz, mit der die Suppe im Teller hin- und herschwappt, gerade mit der eigenen Schrittfrequenz überein, so schaukelt sich diese Schwingung mit jedem Schritt auf, bis die Suppe überschwappt, oder man eben langsamer bzw. schneller geht. Doch nicht bei jedem Überschwappen handelt es sich um Resonanz: Die Frequenz, mit der Kaffee in einer Kaffeetasse hin- und herschwappt (die Eigenfrequenz des Kaffees in der Tasse), liegt deutlich höher als die gewöhnliche Schrittfrequenz, nämlich ungefähr zwei- bis dreimal so hoch. Dennoch passiert es ebenfalls, dass wenn plötzlich jemand um die Ecke kommt, man abrupt anhalten muss und dabei der Kaffee überschwappt. Hier liegt keine periodische Anregung und somit keine Resonanz vor. Der Kaffee schwappt – analog zum nur einmal angestoßenen Pendel – aufgrund von Impulserhaltung über.

Der Drehknopf bei einem Transistorradio mag im Zeitalter der Radios mit automatischer Senderauswahl und vorprogrammierten Programmknöpfen schon etwas in Vergessenheit geraten: mit ihm wird der Drehkondensator in einem LC-Schwingkreis verändert, so dass der Schwingkreis auf eine bestimmte Frequenz eingestellt ist. Radiowellen dieser Frequenz können nun verstärkt werden und die ihnen aufmodulierten kleinen Amplituden- oder Frequenzänderungen (siehe Amplitudenmodulation und Frequenzmodulation) können in das übertragene akustische Signal umgewandelt werden. Die im LC-Schwingkreis eingestellte Resonanzfrequenz filtert dabei gerade die Radiowellen heraus, die auf einer bestimmten Frequenz übertragen wurden.

Die Trommel in einer Waschmaschine ist mit Federn aufgehängt, die mit einer bestimmten Frequenz schwingen können. Ist diese Schwingung schlecht gedämpft, oder bleibt die Waschmaschine -möglicherweise wegen Überladung- beim Anlaufen des Schleudergangs mit ihrer Drehzahl zu lange im Frequenzbereich dieser Schwingung, so schaukelt sich diese aufgrund von Resonanz auf und die ganze Waschmaschine beginnt zu rütteln. Erst wenn eine höhere Drehzahl erreicht ist (und keine Resonanz mehr vorliegt) beruhigt sich dieses Rütteln (aufgrund der Dämpfung), bis am Ende des Schleudergangs wieder der entsprechende Frequenzbereich durchlaufen wird und die Maschine wegen Resonanz erneut zu rütteln beginnt. Typischerweise ist die Wäsche am Ende des Schleudergangs jedoch trockener, erzeugt somit eine geringere Unwucht und das Rütteln am Ende des Schleudergangs ist deutlich schwächer.

Auch lockere Teile in oder an Motoren können eine bestimmte Eigenfrequenz haben. Liegt die Drehzahl des Motors gerade bei dieser Frequenz, so ist das Wackeln solcher Teile oft sehr laut hörbar, was bei anderen Drehzahlen wieder verschwindet.

Resonanz am Beispiel des harmonischen Oszillators

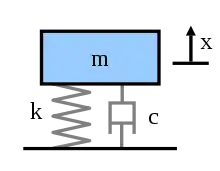
Abbildung 1: Masse-, Feder-, Dämpfer-System

Die mit der Resonanz verbundenen Phänomene lassen sich anhand des harmonischen Oszillators, zum Beispiel eines mechanischen Masse-Feder-Dämpfer-Systems wie nebenstehend abgebildet, betrachten.

Das System wird durch eine periodische Kraft $F(t)$ , die auf die Masse wirkt, angeregt. Es kommt je nach Anfangsbedingungen zu unterschiedlichen Einschwingvorgängen. War das Schwingungssystem vorher in Ruhe, wächst die Amplitude $A$ zunächst an und kann, wenn die Erregerfrequenz in der Nähe seiner Eigenfrequenz liegt, größere Werte erreichen als bei konstantem Einwirken der maximalen Kraft. Sofern das Schwingungssystem nicht überlastet wird (Resonanzkatastrophe) und die Dämpfung nicht exakt Null ist, geht die Schwingung allmählich in eine harmonische Schwingung mit konstanten Werten für Amplitude, Frequenz und Phasenverschiebung gegenüber der Erregerschwingung über. Dieses Verhalten zeigt sich vollkommen übereinstimmend für jede Art von harmonischem Oszillator. In der Realität sind zwar die meisten Systeme, die Schwingungen ausführen können nur näherungsweise harmonisch, doch zeigen sie alle die Resonanzphänomene in zumindest ähnlicher Weise (siehe Anharmonischer Oszillator).

Bewegungsgleichung

Der homogenen Differentialgleichung für einen linear gedämpften harmonischen Oszillator wird eine externe Kraft $F(t)$ hinzugefügt. Die Gleichung wird dadurch inhomogen.

m{\ddot {x}}+c{\dot {x}}+kx=F(t)

Darin bezeichnet $x(t)$ die momentane Auslenkung aus der Ruhelage, $m$ die Masse des Körpers, $k$ die Federkonstante für die rücktreibende Kraft, und $c$ die Dämpfungskonstante (s. Abb. 1).

Ohne äußere Kraft und Dämpfung würde das System mit seiner Eigenkreisfrequenz $\omega _{0}={\sqrt {\tfrac {k}{m}}}$ frei schwingen. Mit Dämpfung $c>0$ führt der komplexe Exponentialansatz ${\tilde {x}}(t)=Ae^{\lambda t}$ schnell zu $\lambda =-\gamma \pm i{\sqrt {\omega _{0}^{2}-\gamma ^{2}}}$ , wobei $\gamma =c/(2m)$ ist. Man erhält als Lösung eine freie gedämpfte Schwingung mit der Kreisfrequenz ${\sqrt {\omega _{0}^{2}-\gamma ^{2}}}$ , deren Amplitude proportional zu $e^{-\gamma t}$ abnimmt.

Konstante Kraft

Eine statische konstante Kraft $F(t)=F_{0}$ eines Erregers hätte eine konstante Auslenkung aus der Ruhelage um $A_{\text{E}}=F_{0}/k$ zur Folge.

Eingeschwungener Zustand für periodische Kraft

Wenn die anregende Kraft sinusförmig mit der Amplitude $F_{0}$ und der Kreisfrequenz $\omega$ verläuft, lässt sie sich als der Imaginärteil von

F(t)=F_{0}e^{\mathrm {i} \omega t}

auffassen.

Als stationäre Lösung mit konstanter Amplitude $A$ d. h. für den eingeschwungenen Zustand erhält man wiederum aus dem komplexen Exponentialansatz

{\tilde {x}}(t)={\frac {\frac {F_{0}}{m}}{\omega _{0}^{2}+2\mathrm {i} \gamma \omega -\omega ^{2}}}\,e^{\mathrm {i} \omega t}

Der Imaginärteil von ${\tilde {x}}(t)$ beschreibt eine harmonische Schwingung

x(t)=A\sin(\omega t-\varphi )

um die Ruhelage $X=0$ . Sie hat die Kreisfrequenz $\omega$ der anregenden Kraft, die (reelle) Amplitude

A={\frac {F_{0}/m}{\sqrt {(\omega _{0}^{2}-\omega ^{2})^{2}+(2\gamma \omega )^{2}}}}\equiv {\frac {1}{\sqrt {(1-\eta ^{2})^{2}+(2\eta D)^{2}}}}\cdot A_{\text{E}}

und eine konstante Phasenverschiebung gegenüber der erregenden Kraft von

\varphi =\arctan \left({\frac {2\omega \gamma }{\omega _{0}^{2}-\omega ^{2}}}\right)\equiv \arctan \left({\frac {2\eta D}{1-\eta ^{2}}}\right)\ .

Darin sind:

$A_{\text{E}}={\tfrac {F_{0}}{k}}$ : die Amplitude des Erregers, d. h. die Auslenkung bei statischem Einwirken der Kraft $F_{0}$ .
$\eta ={\frac {\omega }{\omega _{0}}}$ : die auf die Eigenfrequenz bezogene Erregerfrequenz,
$D={\frac {\gamma }{\omega _{0}}}$ : die auf $\omega _{0}$ bezogene, dimensionslose Lehrsche Dämpfung, die oft auch durch den Gütefaktor $Q={\tfrac {1}{2D}}$ ausgedrückt wird. Der Gütefaktor hat die Bedeutung, dass er die Zahl der Schwingungen angibt, nach denen (in Abwesenheit einer äußeren Kraft) die Amplitude auf $e^{-\pi }\approx 4\,\%$ des Anfangswerts abgeklungen ist (nach ${\tfrac {Q}{\pi }}$ Schwingungen auf ${\tfrac {1}{e}}\approx 37\,\%$ ).

Amplitudenresonanz

Abbildung 2: Amplitudengang

A/A_{\mathrm {E} }

des harmonischen Oszillators für verschieden starke Dämpfung D aufgetragen gegen das Frequenzverhältnis

\omega /\omega _{0}

. Die Schnittpunkte der gepunkteten Linie mit den Resonanzkurven zeigen die Lage der Resonanzfrequenzen.

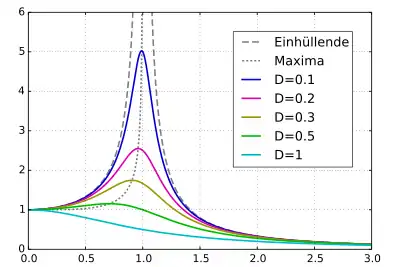
Die Abhängigkeit der Amplitude $A$ von der Erregerfrequenz $\omega$ wird auch als Amplitudengang des Systems bezeichnet. Die Resonanzkurve ist der Graph des Amplitudengangs. Abbildung 2 zeigt das dimensionslose Amplitudenverhältnis ${\tfrac {A(\omega )}{A_{\text{E}}}}$ für typische Wertebereiche der Parameter für Erregerfrequenz (ebenso dimensionslos dargestellt als $\eta =\omega /\omega _{0}$ ) und Dämpfung $D$ .

Bei genügend schwacher Dämpfung, $D<{\sqrt {1/2}}$ , zeigt sich ein Maximum, die Amplitudenresonanz. Sie liegt bei der Resonanzfrequenz $\omega _{\text{res}}=\eta _{\text{res}}\,\omega _{0}={\sqrt {1-2\,D^{2}}}\omega _{0}={\sqrt {\omega _{0}^{2}-2\gamma ^{2}}}$ und zeigt für die maximale Resonanzamplitude den Wert

A_{\text{res}}={\frac {A_{\text{E}}}{2D{\sqrt {1-D^{2}}}}}

.

Das Verhältnis $A_{\text{res}}/A_{\text{E}}$ ist die Resonanzüberhöhung. Die Resonanzfrequenz liegt unter der Eigenkreisfrequenz $\omega _{0}$ des ungedämpften Schwingungssystems und auch unter der Kreisfrequenz $\omega _{d}={\sqrt {\omega _{0}^{2}-\gamma ^{2}}}$ , mit der die freie gedämpfte Schwingung des Systems abläuft.

Bei geringer (aber nicht verschwindender) Dämpfung $0<D\ll {\tfrac {1}{2}}$ ist die Resonanz ein scharfes Maximum, das fast genau bei der Eigenkreisfrequenz liegt. Die Resonanzamplitude $A_{\text{res}}\approx {\tfrac {1}{2D}}A_{\text{E}}$ ist dann umgekehrt proportional zu $D$ . Die Amplitude kann also im eingeschwungenen Zustand ein Vielfaches der statischen Auslenkung $A_{\text{E}}$ erreichen. Während des Einschwingvorgangs aus der Ruhelage heraus kann sie sogar zeitweilig bis auf fast $2A_{\text{res}}$ ansteigen.

Bei starker Dämpfung $D\geq {\sqrt {1/2}}$ hingegen gibt es keine Resonanz mit erhöhter Amplitude. Die maximale Amplitude der eingeschwungenen Schwingung liegt mit dem Wert $A_{\text{E}}$ fest beim statischen Fall $\omega =0$ .

Phasenresonanz und Energiefluss

Bei $\omega =\omega _{0}$ eilt die eingeschwungene Schwingung $x(t)$ der erregenden Kraft um genau 1/4 Periode hinterher (Phasengang −90°, auch als Phasenresonanz bezeichnet). Daher sind Geschwindigkeit ${\dot {x}}(t)$ und Kraft $F(t)$ genau in Phase, sodass die Kraft stets in Richtung der momentanen Geschwindigkeit wirkt. Die Energie fließt dann ständig in das System hinein, während sie bei anderen Frequenzen zweimal pro Periode die Richtung wechselt, weil die Phasendifferenz bei $\omega <\omega _{0}$ kleiner als 90° und bei höherer Frequenz größer als 90° (und bis 180°) ist. Die kinetische Energie des eingeschwungenen Zustands erreicht in der Phasenresonanz ihr Maximum. Sie ist dann so groß wie der gesamte Energieeintrag während der letzten $Q/(2\pi )$ Schwingungen.

Energieresonanz

Die größte potentielle Energie einer Schwingung mit Amplitude $A$ ist $E_{\text{pot}}={\tfrac {1}{2}}\!kA^{2}$ . Die entsprechende Resonanzkurve ist durch das Quadrat des Amplitudengangs gegeben und hat ihr Maximum bei der Frequenz der Amplitudenresonanz $\omega ={\sqrt {\omega _{0}^{2}-2\gamma ^{2}}}$ .

Die größte kinetische Energie in einer Schwingung mit Amplitude $A$ ist $E_{\text{kin}}={\tfrac {1}{2}}m\omega ^{2}A^{2}$ . Diese Funktion hat ihr Maximum genau bei $\omega =\omega _{0}$ .

Bei der für die Optik wichtigen Anwendung auf die Emission und Absorption elektromagnetischer Wellen durch schwingende Dipole ist die Strahlungsleistung $P$ proportional zu ${\tfrac {1}{2}}\omega ^{4}A^{2}$ . Das Maximum dieser Funktion liegt etwas oberhalb $\omega _{0}$ .

Bei scharfen Resonanzen, also geringer Dämpfung, werden die Unterschiede dieser drei Resonanzfrequenzen meist vernachlässigt und für den Bereich der Resonanz eine um die Eigenfrequenz $\omega _{0}$ symmetrische Näherungsformel benutzt, die als Lorentzkurve bezeichnet wird:

A^{2}\approx {\frac {4D^{2}}{(\eta ^{2}-1)^{2}+4D^{2}}}A_{\text{res}}^{2}\equiv {\frac {4\gamma ^{2}\omega _{0}^{2}}{(\omega ^{2}-\omega _{0}^{2})^{2}+4\gamma ^{2}\omega _{0}^{2}}}A_{\text{res}}^{2}

.

Diese Formel zeigt neben der Resonanz auch den für die erzwungene Schwingung charakteristischen langen Ausläufer und ist daher auch für hohe Frequenzen $\eta \gg 1$ bzw. $\omega \gg \omega _{0}$ brauchbar.

Die im Schwingungssystem gespeicherte Energie stammt von der Beschleunigungsarbeit durch die anregende Kraft. Die Schwingungsenergie wird erhöht, wenn die Kraft in Richtung der Geschwindigkeit wirkt. Andernfalls entzieht die Kraft dem System Energie, wirkt also bremsend. Im eingeschwungenen Zustand gleicht der Energieeintrag gerade den Energieverlust aufgrund der Dämpfung aus.

Halbwertsbreite und Gütefaktor

Als Halbwertsbreite $\Delta f_{\text{FWHM}}$ (engl. full width at half maximum) der Resonanz wird der Bereich von Frequenzen $f=\omega /2\pi$ um die Resonanzfrequenz $f_{\text{res}}=\omega _{0}/2\pi$ bezeichnet, in dem für die Amplitude gilt: $A^{2}\geq {\tfrac {1}{2}}A_{\text{res}}^{2}$ . Im interessierenden Bereich geringer Dämpfung liegen nach der Näherungsformel für die Lorentzkurve diese Grenzen bei $\eta =1\pm D$ . Umgerechnet auf die Frequenzachse ergibt sich die Halbwertsbreite

\Delta f_{\text{FWHM}}=2D{\frac {\omega _{0}}{2\pi }}\equiv {\frac {\gamma }{\pi }}

.

Die Schärfe der Resonanz kann mit der Dämpfung oder mit dem Gütefaktor

{\frac {\Delta f_{\text{FWHM}}}{f_{\text{res}}}}=2D={\frac {1}{Q}}

angegeben werden.

Nach der oben angegebenen Bedeutung des Gütefaktors kann man einen Zeitraum von $Q$ Perioden der Eigenfrequenz als charakteristisch für das Abklingen einer gedämpften Eigenschwingung ansehen, also auch charakteristisch für die Dauer des Einschwingvorgangs oder im übertragenen Sinn für das „Gedächtnis des Oszillators“. Analysiert man eine Schwingung mit Frequenz $f_{0}$ mithilfe einer Reihe von Resonatoren zu verschiedenen Resonanzfrequenzen $f$ , dann erfordert die Bestimmung der Resonanzamplitude also die Zeit $\Delta t=Q/f_{0}$ und liefert die Resonanzfrequenz mit der Genauigkeit $\Delta f_{\text{FWHM}}$ . Unterscheiden sich zwei Oszillatoren in der Frequenz um $\Delta f_{\text{FWHM}}$ , dann macht in diesem Zeitraum $\Delta t$ der schnellere gerade eine Schwingung mehr als der langsamere. Es folgt $\Delta t\cdot \Delta f_{\text{FWHM}}=1$ : je genauer die Frequenz einer Schwingung bestimmt werden soll, desto länger muss man sie auf einen Resonator einwirken lassen. Das ist eine frühe Form der Frequenz-Zeit-Unschärferelation.

Resonanz bei Dämpfung Null

Verschwindende Dämpfung ist zwar ein nur theoretischer Grenzfall; reale Systeme mit sehr geringer Dämpfung kommen ihm aber nahe, wenn man sie für einen nicht zu langen Zeitraum $t<1/\gamma$ betrachtet, der jedoch eine große Anzahl $\omega _{0}/(2\pi \gamma )$ von Schwingungen umfassen kann.

Im dämpfungsfreien Fall gibt es keinen Einschwingvorgang, der unabhängig von den Anfangsbedingungen zu einer bestimmten stationären Schwingung führen würde. Eine eventuell mitangeregte Eigenschwingung klingt hier nicht ab, sondern bleibt unvermindert präsent. Bei resonanter Anregung, $\omega =\omega _{0}$ , gibt es keine stationäre Lösung der Bewegungsgleichung, vielmehr variiert die Amplitude linear mit der Zeit. Ausgehend vom Zustand ruhend in der Ruhelage steigt die Amplitude z. B. proportional zur verstrichenen Zeit an:

A(t)={\frac {F_{0}}{2\,m\,\omega _{0}}}\cdot t

Theoretisch kommt es hier also in jedem Fall zur Resonanzkatastrophe. Praktisch ist diese vermeidbar durch eine anderweitig bewirkte Amplitudenbegrenzung, also eine Änderung des Kraftgesetzes (siehe Anharmonischer Oszillator).

Außerhalb der exakten Resonanzfrequenz hingegen existiert zu geeigneten Anfangsbedingungen eine stationäre Schwingung. Sie ergibt sich aus den obigen Gleichungen für $D=0{\text{ bzw. }}\gamma =0$ . Das Amplitudenverhältnis $A(\omega )/A_{\text{E}}$ ist bei jeder Anregungsfrequenz größer als im Fall mit Dämpfung. Bei Resonanz $\omega =\omega _{0}$ divergiert die Formel für die Amplitude und es gibt keinen Zustand der stationären Schwingung. Die Phasenverzögerung ist $\varphi =0^{\circ }$ für Frequenzen unterhalb der Resonanz, $\varphi =180^{\circ }$ oberhalb, wie aus der obigen Formel durch den Grenzübergang $\gamma \rightarrow 0$ hervorgeht. (Für weitere Formeln und Erläuterungen siehe Erzwungene Schwingung#Grenzfall verschwindender Dämpfung.)

Beispiele für das Auftreten von Resonanz

Mechanik

Zungenfrequenzmesser (Ablesung: f ≈ 49,9 Hz)

Bei einem Zungenfrequenzmesser wird derjenige von vielen Biegeschwingern, der mit der Erregerfrequenz in Resonanz ist, zu besonders großer Schwingungsamplitude angeregt.
Kommt eine Brücke in Resonanz mit der Schrittfrequenz von marschierenden Fußgängermassen, kann sich die Konstruktion gefährlich aufschaukeln, Beispiel Millennium Bridge (London)
Fahrzeugkarosserien neigen bei bestimmten Motordrehzahlen zu starken Vibrationen (Dröhnen)
Bahnresonanz kann bei Planeten dafür sorgen, dass ein Himmelskörper auf Kollisionskurs mit einem anderen gerät. An Lagrange-Punkten kann diese Resonanz stabilisierend wirken, beispielsweise bleibt der Sonnenbeobachtungssatellit SOHO seit 1995 immer in der Nähe des inneren Lagrange-Punktes L₁.
Zur Erzeugung von Ultraschall für medizinische oder technische Anwendungen werden elektromechanische, meist piezoelektrische, Wandler zu resonanten Schwingungen angeregt.
Ein Ultraschallbohrer bringt das zu bohrende Gestein in Resonanz, wodurch das Gestein zerbröselt.

Hydromechanik

Akustik

Betrag der akustischen Flussimpedanz eines luftgefüllten kurzen, dünnen Rohres als Funktion der Frequenz. Einheit der vertikalen Skala ist Pa·s/m³

die Tonerzeugung bei Musikinstrumenten (Streich- und Blasinstrumenten), siehe z. B. Holzblasinstrument, Resonanzboden
das Mitschwingen einer nicht gespielten Saite, wenn ein gleichgestimmtes Instrument ertönt (z. B. Resonanzsaite)
In geschlossenen Räumen kann es bei bestimmten Frequenzen zu störender Raumresonanz kommen.
Ein Resonanzauspuff ermöglicht bei Zweitakt-Motoren bei einer ganz bestimmten Drehzahl eine gewisse Leistungssteigerung.

Akustische Resonanz spielt beispielsweise bei fast allen Musikinstrumenten eine Rolle, oft durch Bildung einer stehenden Welle.

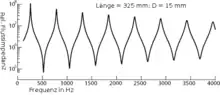
Misst man am Ende eines beiderseits offenen, zylindrischen Rohres mit geeigneten Mikrophonen Schalldruck und Schallschnelle, kann man bei Kenntnis des Rohrquerschnitts die akustische Flussimpedanz berechnen.[11] Diese zeigt Mehrfachresonanzen, wie man sie auch bei der Ausbreitung elektromagnetischer Wellen entlang Drähten als Sonderfall λ/2 kennt. Das Messergebnis im Bild zeigt mehrere scharfe Minima der Flussimpedanz bei Vielfachen der Frequenz 500 Hz. Eine Überprüfung mit der Rohrlänge von 325 mm und der Schallgeschwindigkeit in Luft ergibt den Sollwert 528 Hz.

Weil der Messwert des tiefsten Minimums mit etwa 40000 Pa·s/m³ von der Schallkennimpedanz der umgebenden Luft (413,5 Pa·s/m³) erheblich abweicht, liegt eine Fehlanpassung vor und die schwingende Luftsäule im Rohr ist nur leise hörbar. Dieser geringe Energieverlust drückt sich in einem hohen Gütefaktor des Resonators aus.

Elektrotechnik

Ohne Resonanz gäbe es keine Funktechnik mit den bekannten Teilgebieten Fernsehen, Mobiltelefon, Radar, Funkfernsteuerung und Radioastronomie, weil es ohne die Möglichkeit, Sendefrequenzen voneinander zu trennen, weltweit nur wenige vereinzelte Sender mit ausreichenden Abständen geben könnte. Im überwiegenden Teil aller Oszillatorschaltungen und elektrischen Filter werden Schwingkreise verwendet, denen die Thomsonsche Schwingungsgleichung zur Resonanzfrequenz

\omega _{0}={\frac {1}{\sqrt {LC}}}

zu Grunde liegt. Der Wirkungsgrad von Antennen und Tesla-Transformatoren wird durch Resonanz drastisch gesteigert.

Die Sicherheit im Eisenbahnnetz wird durch die induktive Zugbeeinflussung verbessert. Dabei tritt ein am Fahrzeug angebrachter Schwingkreis in resonante Wechselwirkung mit einem am Gleis angebrachten Schwingkreis, dessen Frequenz je nach Stellung des nächsten Bahnsignals verschieden ist; bei Signalstellung „Halt“ wird eine Zwangsbremsung ausgelöst.

Die großen Teilchenbeschleuniger der Elementarteilchenphysik beruhen auf Resonanzeffekten, ebenso die Kernspinresonanzspektroskopie in der Chemie und die Magnetresonanztomographie in der Medizin.

RFIDs, umgangssprachlich auch Funketiketten genannt, ermöglicht die automatische Identifizierung und Lokalisierung von Gegenständen und Lebewesen. Dabei wird die Betriebsenergie durch Resonanz auf das RFID übertragen und dieses sendet seine Information auf gleichem Weg zurück.

Ein Absorptionsfrequenzmesser wirkt bei Resonanz wie ein selektives Voltmeter.

Ein Magnetron erzeugt nur dann Schwingungen, wenn die Umlaufgeschwindigkeit mit der Eigenfrequenz der Hohlraumresonatoren übereinstimmt.

Atom- und Molekülphysik

Schematische Darstellung eines Zweizustandssystems, das mit elektromagnetischer Strahlung wechselwirkt.

Termschema des Wasserstoffatoms: Die durch Pfeile angedeuteten Übergänge können mit zu ihrer Energiedifferenz resonantem Licht angeregt werden

Empfindlichkeit der Zapfen des menschlichen Auges. S:Blau, M:Grün, L:Rot, Z: Gesamt

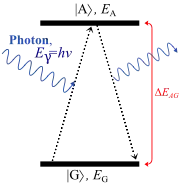
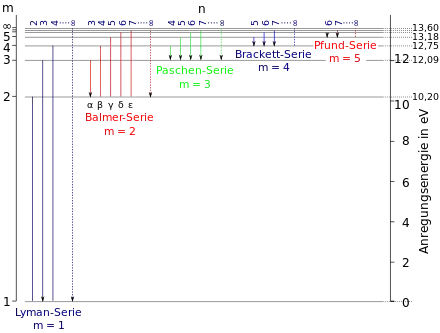
In der Atom- und Molekülphysik spricht man von Resonanz, wenn ein Photon der Energie $E_{\gamma }=h\cdot \nu$ (h: Plancksches Wirkungsquantum, ν: Frequenz des Lichtes) in der Hülle des Atoms absorbiert wird. Dies ist nur möglich, wenn $E_{\gamma }$ gerade gleich der Energiedifferenz $\Delta E_{\mathrm {GA} }=E_{\mathrm {A} }-E_{\mathrm {G} }$ zwischen zwei Zuständen G und A der Elektronenhülle ist. Ein Elektron wird dann vom Zustand G in den Zustand A angehoben. Die Anregungswahrscheinlichkeit $p_{\mathrm {GA} }(E_{\gamma })$ eines solchen Überganges wird durch eine Lorentzkurve beschrieben:

p_{\mathrm {GA} }(E_{\gamma })\propto {\frac {1}{\left|(1+(E_{\gamma }/\Delta E_{\mathrm {GA} })^{2})\right|}}

Der Vorgang heißt Resonanzabsorption. Er erklärt beispielsweise die Fraunhoferlinien im Spektrum des Sonnenlichts.

Meist fällt nun das Elektron aus dem angeregten Zustand zurück in den Grundzustand, wobei wieder ein Photon der Energie $E_{\gamma }=E_{\mathrm {GA} }$ ausgesandt wird. Dies geschieht entweder spontan (spontane Emission, Fluoreszenz, Phosphoreszenz) oder durch Stoß eines zweiten eingestrahlten Photons der gleichen Energie (stimulierte Emission, ausgenutzt beim Laser).

Aus dem Grundzustand kann das Atom nun wieder angeregt werden. Es kann also eine Besetzungszahloszillation zwischen den Zuständen G und A ausführen, die als Rabi-Oszillation bezeichnet wird. Die Oszillation tritt, wie erwähnt, nur dann auf, wenn die eingestrahlten Photonen in Resonanz mit den Energieniveaus eines Atoms sind. Solche Resonanzen können z. B. zur Identifizierung von Gasen in der Spektroskopie verwendet werden, da sie das Vermessen der atom- oder molekültypischen Energieniveaus erlauben.

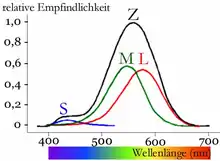
Im menschlichen Auge gibt es drei verschiedene Arten von Zapfen (Farbrezeptoren). Die darin enthaltenen Opsin-Moleküle unterscheiden sich durch ihre spektrale Empfindlichkeit und setzen bei Resonanz mit Photonen geeigneter Wellenlänge intrazelluläre Signalkaskaden in Gang (s. Phototransduktion). Es werden elektrische Signale gebildet, die über die Ganglienzellen an das Gehirn weitergegeben werden. Dort entsteht aus den übermittelten Signalen ein Farbeindruck (s. Farbwahrnehmung).

Weitere Resonanzphänomene treten bei der Kopplung des magnetischen Moments eines Atoms, Atomkerns, Moleküls oder Elektrons (Spin) an ein Magnetfeld auf, zum Beispiel Elektronenspinresonanz und Kernspinresonanz. Dabei regt ein mit passender Frequenz oszillierendes Magnetfeld das Umklappen des Spins zwischen zwei diskreten Zuständen verschiedener Energie an. Auch dieser Effekt kann entsprechend den Rabi-Oszillationen beschrieben werden und wird z. B. in der Medizintechnik und zu Materialuntersuchungen eingesetzt (siehe z. B. Magnetresonanztomographie).

Kernphysik

Resonanz bedeutet in der Kernphysik, dass bei einem Stoßvorgang mit bestimmter kinetischer Energie die beiden Partner sich zu einem kurzzeitig gebundenen System, dem Compoundkern, in einem seiner möglichen Energiezustände vereinigen. Der Wirkungsquerschnitt zeigt bei dieser Stoßenergie ein Maximum von der Form einer Breit-Wigner-Kurve, die der für Resonanzen typischen Lorentzkurve gleicht.

Ein solches System kann nicht stabil sein, sondern zerfällt nach kurzer Zeit wieder, z. B. in die beiden Teilchen, aus denen es gebildet wurde. Doch lässt sich aus der Zerfallsbreite der Kurve entnehmen, dass es wesentlich länger existiert hat, als einer Reaktion der Teilchen im Vorbeiflug entsprechen würde.

Alle größeren Kerne zeigen die Riesenresonanz, einen angeregten Zustand, bei dem die Protonen gemeinsam gegenüber den Neutronen schwingen.

Die Resonanzabsorption von Gammaquanten ermöglicht durch Ausnutzung des Dopplereffekts den Vergleich von Anregungsenergien mit einer Genauigkeit von mehr als 10¹². Atomkerne sind Resonatoren mit z. T. extrem hohen Gütefaktoren von 10¹² und aufwärts (z. B. Gütefaktor von ⁹⁹Tc: 6,8·10²⁴).

Teilchenphysik

Ähnlich wie bei der Compoundkernbildung kann aus zwei Stoßpartnern ein instabiles, aber vergleichsweise langlebiges gebundenes System oder sogar ein einziges, andersartiges Teilchen entstehen, wenn die Stoßenergie im Schwerpunktsystem gerade dazu ausreicht. Dieser Fall wird auch als Resonanzproduktion bezeichnet. Die Anregungsfunktion des Stoßprozesses, also sein Wirkungsquerschnitt aufgetragen als Funktion der Energie, zeigt dann bei dieser Energie ein Maximum mit der für eine Resonanz typischen Kurvenform. So gebildete Systeme werden häufig als Resonanz oder Resonanzteilchen bezeichnet. Aus der Halbwertsbreite der Kurve (siehe Zerfallsbreite) kann die – für eine direkte Messung zu kurze – Lebensdauer des entstandenen Teilchens bestimmt werden.

Siehe auch

Wiktionary: resonant – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: Resonanz

Einzelnachweise

Andrea Frova, Mariapiera Marenzana: Thus spoke Galileo. The great scientist's ideas and their relevance to the present day. Oxford University Press, Oxford u. a. 2006, ISBN 0-19-856625-5, S. 133–137.
Stillman Drake: Essays on Galileo and the history and philosophy of science. Band 1. Selected and introduced by Noel M. Swerdlow and Trevor H. Levere. University of Toronto Press, Toronto u. a. 1999, ISBN 0-8020-7585-1, S. 41–42.
Leonhard Euler: Brief vom 5. (16.) Mai 1739 (Nr. 23) an Johann Bernoulli. In: Emil A. Fellmann, Gleb K. Mikhajlov (Hrsg.): Euler: Opera Ommnia (= Briefwechsel Series Quarta A Commercium Epistolicum). Band II. Birkhäuser, Basel 1998, S. 58, 303 (online).
Thomas Young: Tides: From the Supplement to the Encyclopedia Britannica 1823: Abgedruckt in: Peacock, George (Hg.) (1855). Miscellaneous works of the late Thomas Young. London: J. Murray. Band 2, S. 291 ff.
Anton Oberbeck: Ueber eine der Resonanz ähnliche Erscheinung bei electrischen Schwingungen. In: Annalen der Physik. Band 262, Nr. 10, 1885, S. 245–253.
Johann Friedrich Radinger: Über Dampfmaschinen mit hoher Kolbengeschwindigkeit. Druck und Verlag von Carl Gerold's Sohn, 1892.
Arnold Sommerfeld: Die naturwissenschaftlichen Ergebnisse und die Ziele der modernen technischen Mechanik. In: Naturwissenschaftliche Rundschau. Band 49, 1903, S. 621–624.
Armin Hermann: Der Brückenschlag zwischen Mathematik und Technik: Arnold Sommerfelds Verdienste um eine wissenschaftliche technische Mechanik. In: Physikalische Blätter. Band 23, Nr. 10, 1967, S. 442–449.
Mark Buchanan: Going into resonance. In: Nature Physics. Band 15, Nr. 3, 2019, S. 203. (engl., abgerufen 19. Juli 2020)
Jörn Bleck-Neuhaus: Mechanical resonance: 300 years from discovery to the full understanding of its importance. Abgerufen am 19. Juli 2020. (engl.)
Messung der akustischen Flussimpedanz (englisch; PDF; 856 kB)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Andrea Frova, Mariapiera Marenzana: Thus spoke Galileo. The great scientist's ideas and their relevance to the present day. Oxford University Press, Oxford u. a. 2006, ISBN 0-19-856625-5, S. 133–137.

[2] Stillman Drake: Essays on Galileo and the history and philosophy of science. Band 1. Selected and introduced by Noel M. Swerdlow and Trevor H. Levere. University of Toronto Press, Toronto u. a. 1999, ISBN 0-8020-7585-1, S. 41–42.

[3] Leonhard Euler: Brief vom 5. (16.) Mai 1739 (Nr. 23) an Johann Bernoulli. In: Emil A. Fellmann, Gleb K. Mikhajlov (Hrsg.): Euler: Opera Ommnia (= Briefwechsel Series Quarta A Commercium Epistolicum). Band II. Birkhäuser, Basel 1998, S. 58, 303 (online).

[4] Thomas Young: Tides: From the Supplement to the Encyclopedia Britannica 1823: Abgedruckt in: Peacock, George (Hg.) (1855). Miscellaneous works of the late Thomas Young. London: J. Murray. Band 2, S. 291 ff.

[5] Anton Oberbeck: Ueber eine der Resonanz ähnliche Erscheinung bei electrischen Schwingungen. In: Annalen der Physik. Band 262, Nr. 10, 1885, S. 245–253.

[6] Johann Friedrich Radinger: Über Dampfmaschinen mit hoher Kolbengeschwindigkeit. Druck und Verlag von Carl Gerold's Sohn, 1892.

[7] Arnold Sommerfeld: Die naturwissenschaftlichen Ergebnisse und die Ziele der modernen technischen Mechanik. In: Naturwissenschaftliche Rundschau. Band 49, 1903, S. 621–624.

[8] Armin Hermann: Der Brückenschlag zwischen Mathematik und Technik: Arnold Sommerfelds Verdienste um eine wissenschaftliche technische Mechanik. In: Physikalische Blätter. Band 23, Nr. 10, 1967, S. 442–449.

[9] Mark Buchanan: Going into resonance. In: Nature Physics. Band 15, Nr. 3, 2019, S. 203. (engl., abgerufen 19. Juli 2020)

[10] Jörn Bleck-Neuhaus: Mechanical resonance: 300 years from discovery to the full understanding of its importance. Abgerufen am 19. Juli 2020. (engl.)

[11] Messung der akustischen Flussimpedanz (englisch; PDF; 856 kB)