Sternaufbau

Die Modellierung des Sternaufbaus ist ein astrophysikalisches Problem. Ein Stern ist eine massereiche Kugel aus glühendem Gas, die sich durch die eigene Schwerkraft zusammenhält. Im dichten Zentrum wird durch Kernfusion Energie frei, deren Leistung als Leuchtkraft des Sterns gegeben ist.

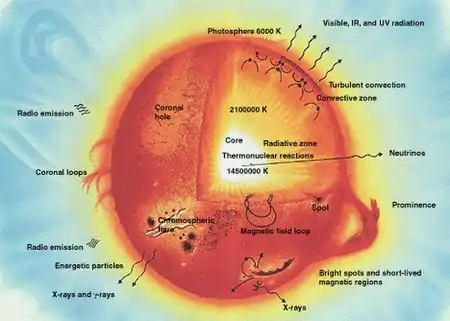
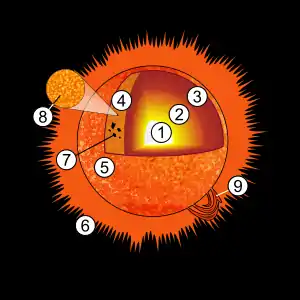
Diese Grafik zeigt einen Querschnitt durch einen sonnenähnlichen Hauptreihenstern. NASA image

Schnittdiagramm der Sonne:
1. Kern
2. Strahlungszone
3. Konvektionszone
4. Photosphäre
5. Chromosphäre
6. Corona
7. Sonnenfleck
8. Granulation
9. Protuberanz

Aus seinem Farbindex ist die Temperatur der Sternoberfläche bekannt und aus dem Linienspektrum deren Metallizität. Die Temperaturabhängigkeit der Kernreaktionen wird seit den 1930er Jahren mit Teilchenbeschleunigern immer genauer bestimmt, sodass auch der Zustand in der Kernzone des Sterns nicht völlig unbestimmt ist. Im Fall der Sonne sind zusätzlich Masse und Durchmesser bekannt.

Bereits 1925 stellte Arthur Stanley Eddington ein einigermaßen zutreffendes Modell der Sonne auf.[1] Dessen grundlegende Gleichungen sind zwar einfach, insbesondere dominieren für sonnenähnliche Sterne die Gasgesetze, jedoch sind in weiten Teilen eines Sterns die physikalischen Bedingungen so extrem, dass wichtige Materialeigenschaften nicht im Labor ermittelt werden können. Sie müssen mit theoretischen Ansätzen aus dem Gebiet der kondensierten Materie berechnet werden. Das betrifft insbesondere die Opazität, die den Strahlungstransport der Fusionswärme behindert. Sie variiert nicht nur mit der Dichte, sondern hängt über den Ionisationszustand vor allem der schwereren Elemente auch von der Temperatur ab.

Großen numerischen Aufwand erfordert es, die Änderung der chemischen Zusammensetzung des Kerns insbesondere in den Spätstadien der Sternentwicklung und die Magneto-Hydrodynamik in turbulenten Bereichen der Konvektionszone zu berücksichtigen.

Prüfsteine für Sternmodelle sind insbesondere pulsationsveränderliche Sterne und in neuerer Zeit die Helioseismologie.

Grundgleichungen des Sternaufbaus

Ziel dieser Gleichungen ist es, die Schichtung der Sternmaterie zu beschreiben, d. h. das Verhalten von Druck, Temperatur, Dichte, Leuchtkraft, Energieerzeugung und chemischer Zusammensetzung mit zunehmender Tiefe. Hierbei werden oft folgende Vereinfachungen getroffen:

Kugelsymmetrie

Die einfachste geometrische Konfiguration ist das kugelsymmetrische Modell. Es geht davon aus, dass der Stern nicht rotiert, so dass keine ausgezeichnete Achse vorliegt. Dieses Vorgehen ist nur für langsam rotierende Sterne wie die Sonne zulässig. Junge, massereiche Sterne haben oft hohe Rotationsgeschwindigkeiten. Eine systematische Diskussion der Rotation aller Sterntypen und ihres Einflusses auf deren inneren Aufbau und Entwicklung gibt Tassoul (2000).

Hydrostatisches Gleichgewicht

Hierbei nimmt man an, dass sich der Stern in einem eingeschwungenen Zustand befindet und die auf der Gravitation und dem inneren Druck der Sternmaterie beruhenden Kräfte sich exakt ausgleichen. Diese Annahme eines quasistatischen Zustandes ist für die meisten Sterne gerechtfertigt. Ausnahmen sind das Kontraktionsstadium während der Sternentstehung, pulsierende Riesen und Überriesen und ganz besonders der Gravitationskollaps nach dem Versiegen der für die Kernfusion notwendigen leichten Elemente.

Masseerhaltung

Oft wird auch angenommen, dass die Masse eines Sterns konstant ist. Dies ist abermals nur für massearme Sterne auf der Hauptreihe wie die Sonne zulässig. Zwar erleiden auch solche Sterne einen Massenverlust (durch die Kernfusion und auch durch die Partikelstrahlung), doch ist dieser im Vergleich zur Gesamtmasse bedeutungslos. Massereiche Hauptreihensterne und (Über)riesen können jedoch schon auf einer Zeitskala von nur einer Million Jahren einen signifikanten Teil ihrer Masse durch andauernden Materieauswurf verlieren. De Jager u. a. (1988) untersuchten dies erstmals systematisch, indem sie Massenverlustraten von zahlreichen Sternen aller Typen bestimmten.

Lokales thermisches Gleichgewicht

Hier setzt man voraus, dass jeder Punkt des Sterninneren sich mit seiner Umgebung im Strahlungsgleichgewicht befindet (d. h. ebenso viel Energie abgibt wie er empfängt), sodass die beiden Komponenten Materie und Strahlung an jedem Ort die gleiche Temperatur haben. Streng genommen wird lokales thermisches Gleichgewicht nie wirklich erreicht, da die Temperatur unterhalb einer betrachteten Schicht stets höher ist als die Temperatur darüber. Meist ist die Näherung jedoch sehr genau, da die mittlere freie Weglänge $l$ der Photonen klein ist verglichen mit der Strecke, über die sich die Temperatur merklich ändert, d. h. $l\ll T/|\nabla T|$ .

Klassen von Gleichungen

Der Sternaufbau wird durch zwei Klassen von Gleichungen behandelt. Mehrere Differentialgleichungen beschreiben die Änderung der physikalischen Gegebenheiten mit der Tiefe, hinzu treten Materialgleichungen.

Differentialgleichungen

Bei den Differentialgleichungen handelt es sich um ein System von vier gekoppelten Gleichungen erster Ordnung. Wenn Kugelsymmetrie vorausgesetzt werden darf, erscheint der Radius $r$ als einzige Variable, d. h., der Stern wird als eine Anordnung von kugelförmigen dünnen Schalen betrachtet. Zwei Gleichungen beschreiben die Schichtung des Druckes $p(r)$ und die Verteilung der Masse $m(r)$ . Zwei weitere Gleichungen geben die Energiebilanz und damit die Leuchtkraft $L(r)$ sowie die Temperaturschichtung $T(r)$ an. Die Gleichungen des Sternaufbaus werden in vielen Lehrbüchern der Astrophysik behandelt, z. B. von Kippenhahn und Weigert (1990), Zeilik und Gregory (1998) und Hansen u. a. (2004).

Materialgleichungen

Zusätzlich zu den Differentialgleichungen werden noch weitere Beziehungen benötigt, die Materialeigenschaften beschreiben. So müssen Druck, Dichte und Temperatur durch eine Zustandsgleichung miteinander verknüpft werden. Während bei Hauptreihensternen zumeist die allgemeine Gasgleichung angewandt werden darf, müssen die extrem verdichteten Kerne von (Über-)Riesen und ganz besonders die Endstadien wie weißer Zwerg und Neutronenstern als entartete Materie behandelt werden (wo keine Temperaturabhängigkeit, sondern nur noch eine Dichteabhängigkeit des Druckes vorliegt). Für die Energieerzeugung muss ebenfalls die Abhängigkeit von anderen Größen angegeben werden, insbesondere von der Temperatur und Dichte. Um die Temperaturschichtung korrekt zu beschreiben, muss der Mechanismus des Energietransports gegeben sein. Der Energiestrom kann sowohl durch Strahlung als auch Konvektion erfolgen. Im ersten Fall müssen als weitere Materialeigenschaften die Durchsichtigkeit (die sogenannte Opazität) und das davon abgeleitete Strahlungsleitvermögen der Sternmaterie bekannt sein. Auch sie sind temperatur- und dichteabhängig. Im letzteren Fall tritt zum Energiestrom ein Massestrom hinzu, so dass auch die Hydrodynamik in das Problem des Sternaufbaus Eingang findet.

Masseerhaltung und hydrostatische Grundgleichung

Die beiden folgenden Gleichungen beschreiben wie bereits angedeutet die Verteilung der Masse sowie die Druckschichtung im Sterninneren.

Masseerhaltung

Die Gleichung für die Massenverteilung ist am einfachsten zu verstehen. Eine dünne Kugelschale mit Radius $r$ und Dicke $dr$ hat ein Volumen $4\pi r^{2}dr$ . Zusammen mit der Dichte $\rho (r)$ ergibt sich daraus für deren Masse $m(r)$ :

{\frac {\mathrm {d} m(r)}{\mathrm {d} r}}=4\pi r^{2}\rho (r)

Die Integration von $r=0$ bis zum äußeren Rand des Sterns $r=R$ ergibt dessen Gesamtmasse $M$ .

Hydrostatische Grundgleichung

Die für die Masseerhaltung betrachtete Kugelschale hat pro Fläche eine Masse $\rho (r)dr$ und eine Gewichtskraft $g(r)\rho (r)dr$ , wobei $g(r)$ die Fallbeschleunigung im Abstand $r$ vom Sternzentrum bedeutet. Nach dem Birkhoff-Theorem, das in seiner klassischen Form schon Isaac Newton zeigte, trägt bei einer kugelsymmetrischen Masseverteilung nur diejenige Masse $m(r)$ zur Fallbeschleunigung bei, die sich innerhalb von $r$ befindet. Damit ist einfach $g(r)=Gm(r)/r^{2}$ , wobei $G$ die Gravitationskonstante bedeutet. Einsetzen liefert für das Gewicht pro Fläche, also den ausgeübten Druck:

{\frac {\mathrm {d} p(r)}{\mathrm {d} r}}=-{\frac {Gm(r)\rho (r)}{r^{2}}}

Elementare Beispiele und Schlussfolgerungen

Aus den obigen beiden Differentialgleichungen können mittels einer elementaren Abschätzung bereits einige wichtige Zusammenhänge zwischen den Bedingungen im Sterninneren und beobachtbaren Zustandsgrößen hergestellt werden. Gibt man ein plausibles Dichtegesetz $\rho (r)$ einfach vor, lassen sich die Gleichungen elementar lösen und so die mittlere Dichte $\langle \rho \rangle$ , die zentrale Dichte $\rho _{c}$ und der zentrale Druck $p_{c}$ abschätzen.

Das denkbar einfachste Modell ist das einer konstanten Sterndichte (damit sind natürlich $\langle \rho \rangle$ und $\rho _{c}$ identisch). Einsetzen in die Massenerhaltung und Integration liefern:

m(r)={\frac {4\pi }{3}}\rho _{c}r^{3}

Die Integrationskonstante muss so gewählt werden, dass $m(0)=0$ . Setzt man $r=R$ , so findet man folgende Beziehung:

\rho _{c}={\frac {3}{4\pi }}{\frac {M}{R^{3}}}

Für die Sonne erhält man mit $M$ = 1,989 × 10³⁰ kg und $R$ = 696.000 km den Wert $\rho _{c}$ = 1,41 g/cm³. Eine exakte Behandlung des Problems liefert mit $\rho _{c}$ = 162 g/cm³ einen viel höheren Wert, d. h., tatsächlich nimmt mit zunehmender Tiefe die Dichte stark zu. Dies ist zu erwarten, da der Druck mit der Tiefe ebenfalls zunimmt und die Sternmaterie kompressibel ist. Eine Zusammenstellung der Zustandsgrößen der Sonne findet sich auf der NASA Website Sun Fact Sheet (siehe Weblinks).

Die hier abgeleitete Proportionalität

\rho _{c}\propto {\frac {M}{R^{3}}}

gilt jedoch für beliebige kugelsymmetrische Dichteverteilungen innerhalb von Hauptreihensternen, wie Schwarzschild (1958) zeigte. Die zentrale Dichte ist also der Masse eines solchen Objekts direkt und seinem Volumen umgekehrt proportional. Überraschenderweise dominiert hier der Volumenterm gegenüber dem Masseterm, d. h. nicht massereiche, sondern massearme Sterne weisen höhere zentrale Dichten auf! Scheffler und Elsässer (1990) geben für einen Hauptreihenstern des Spektraltyps M0 eine Masse von 0,5 Sonnenmassen und einen Radius von 0,6 Sonnenradien an, also ein Verhältnis $M/R^{3}$ von 2,3. Ein O5-Stern weist 50 Sonnenmassen und 12 Sonnenradien auf, damit liegt $M/R^{3}$ bei 0,029.

Erklären lässt sich dieses Verhalten anhand der Tatsache, dass die Zentraltemperatur massearmer Sterne wesentlich geringer ist als die massereicher Sterne (was im nachfolgenden Abschnitt gezeigt wird). Ein Gleichgewicht zwischen Gasdruck und Gravitationsdruck kann sich ungeachtet der geringeren auf den Kern lastenden Masse daher nur dann einstellen, wenn die Materie stärker komprimiert wird.

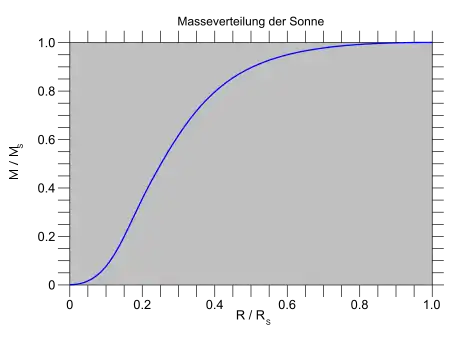
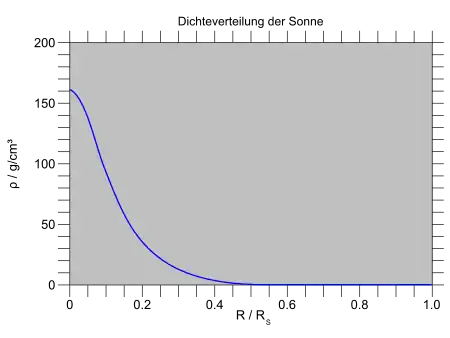
Ein realistisches Modell für die Verteilungen von Masse und Dichte im Sonneninneren zeigen die folgenden Diagramme, die auf den von Abraham und Iben (1971) gegebenen Werten beruhen. Demnach ist die Materie sehr stark zum Zentrum hin konzentriert. Innerhalb ein Viertel des Sonnenradius, d. h. 1/64 des Sonnenvolumens, befindet sich bereits die halbe Sonnenmasse! Dementsprechend nimmt auch die Dichte sehr stark zur Sonnenmitte hin zu. Bei einem Abstand von einem halben Sonnenradius vom Zentrum ist die Dichte des Wassers erreicht. Bis zum Zentrum selbst steigt die Dichte noch einmal um mehr als das 100-Fache an.

Einsetzen der konstanten Dichte und der entsprechenden Masseverteilung in die hydrostatische Grundgleichung und Integration liefert:

p(r)=p_{c}-{\frac {2\pi }{3}}G\rho _{c}^{2}r^{2}

Mit der Forderung $p(R)=0$ gewinnt man folgenden Zusammenhang:

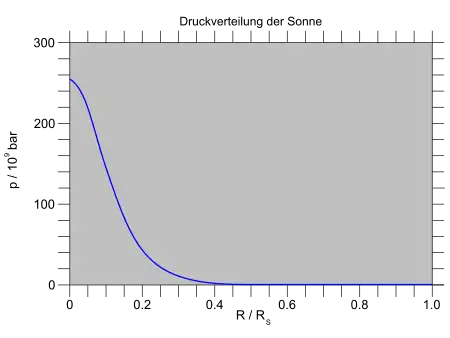
p_{c}={\frac {2\pi }{3}}G\rho _{c}^{2}R^{2}={\frac {3}{8\pi }}G{\frac {M^{2}}{R^{4}}}

Setzt man Sonnenmasse und Sonnenradius ein, so erhält man $p_{c}$ = 1,34 × 10⁹ bar, wohingegen die exakte Theorie $p_{c}$ = 2,48 × 10¹¹ bar liefert. Die Unterschätzung der zentralen Dichte zieht auch eine Unterschätzung des zentralen Druckes nach sich.

Wieder ist nach Schwarzschild die gezeigte Proportionalität

p_{c}\propto {\frac {M^{2}}{R^{4}}}

für Hauptreihensterne allgemeingültig. Der zentrale Druck wächst also quadratisch mit der Sternmasse und fällt mit der vierten Potenz des Sternradius. Auch hier dominiert der Radiusterm noch gegenüber dem Masseterm. Wieder sind es die massearmen, nicht die massereichen Sterne, welche die höheren zentralen Drücke aufweisen! Betrachtet man erneut Hauptreihensterne der Typen M0 und O5, so liegt $M^{2}/R^{4}$ bei 1,9 und 0,12. Die geringeren zentralen Dichten in massereichen Sternen dominieren noch gegenüber den höheren Zentraltemperaturen.

Auch für den Druck sei das Sonnenmodell von Abraham und Iben (1971) gezeigt. Entsprechend der starken Massekonzentration zur Mitte hin nimmt dort der Druck sehr stark zu. Der Anstieg ist noch steiler als für die Dichte. Vergleicht man den Druck bei einem Abstand von einem halben Sonnenradius vom Zentrum mit dem Druck in der Sonnenmitte selbst, ergibt sich ein Anstieg um nahezu einen Faktor 500.

Zustandsgleichung

Die Zustandsgleichung verbindet Dichte, Druck und Temperatur miteinander. Bei massereichen Sternen muss außer dem Gasdruck auch der Strahlungsdruck beachtet werden.

Gasdruck

Bei Hauptreihensternen darf als Zustandsgleichung die allgemeine Gasgleichung verwendet werden. Sie lautet:

p_{G}={\frac {\rho kT}{\mu }}

Hierbei bezeichnet $k$ die Boltzmannkonstante und $\mu$ die mittlere molare Masse. Um Letztere zu bestimmen, muss die Ionisation der Sternmaterie berücksichtigt werden, die aber wiederum eine Funktion der Temperatur und auch des Druckes ist. In der Kernzone kann generell von vollständiger Ionisation ausgegangen werden, in den oberflächennahen Schichten ist vor allem bei kühlen Sternen die Materie aber nur noch teilweise ionisiert. Wegen der Dominanz der leichtesten Elemente teilt man die Sternmaterie in drei Teilchen-Anteile ein, den Wasserstoff-Anteil X, den Helium-Anteil Y sowie den Anteil Z aller sonstigen Elemente. Bei vollständiger Ionisation beträgt die mittlere Atommasse des Wasserstoffs $\mu _{\mathrm {H} }=u/2$ , diejenige des Heliums $\mu _{\mathrm {He} }=4u/3$ . Für ein beliebiges völlig ionisiertes Element mit P Protonen und N Neutronen gilt $\mu _{Z}=(P+N)/(P+1)u\approx 2u$ . Damit ist die über alle Elemente gemittelte molare Masse:

\mu =\left({\frac {1}{2}}X+{\frac {4}{3}}Y+2Z\right)u

u steht für die atomare Masseneinheit. Für die Sonne liegt bei vollständiger Ionisation die mittlere molare Masse etwa bei 0,8 u.

Strahlungsdruck

Der Strahlungsdruck ist eine alleinige Funktion der Temperatur:

p_{S}={\frac {1}{3}}aT^{4}

a = 7,56 × 10⁻¹⁶ J m⁻³ K⁻⁴ ist eine Naturkonstante (siehe Stefan-Boltzmann-Gesetz).

Elementare Beispiele und Schlussfolgerungen

Mit Hilfe der obigen Abschätzungen für die zentrale Dichte und den Druck gewinnt man auch eine solche der Temperatur. Einsetzen des Gravitationsdruckes in die allgemeine Gasgleichung liefert:

T_{c}(p_{G})={\frac {1}{2}}{\frac {\mu }{k}}G{\frac {M}{R}}

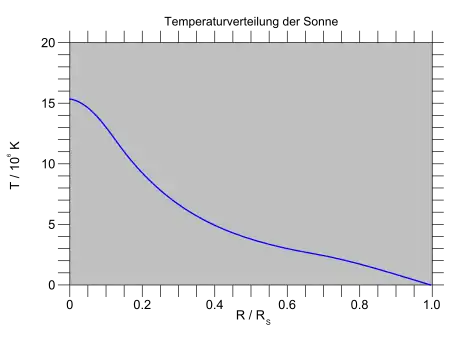
Für die Sonne erhält man damit $T_{c}$ = 9,3 × 10⁶ K. Die exakte Theorie führt auf $T_{c}$ = 15,7 × 10⁶ K. Die Abweichung der elementaren Abschätzung ist hier geringer, weil die Fehler von Dichte und Druck sich im Quotienten zum Teil gegenseitig aufheben.

Der Zusammenhang

T_{c}(p_{G})\propto {\frac {M}{R}}

zeigt, dass bei Dominanz des Gasdrucks die Zentraltemperatur der Masse direkt und dem Radius umgekehrt proportional ist. Jetzt dominiert die Masse gegenüber dem Radius. Für Hauptreihensterne der Typen M0 und O5 liegt $M/R$ bei 0,83 und 4,17.

Insgesamt ergibt sich also ein Anstieg der Temperatur zu höheren Sternmassen hin. Umgekehrt bedeutet dies, dass unterhalb einer gewissen Mindestmasse die Zentraltemperatur (trotz höherer Zentraldichte) nicht mehr ausreicht, um das für Hauptreihensterne typische Wasserstoffbrennen im Kern in Gang zu setzen. Diese Mindestmasse liegt bei etwa 0,08 Sonnenmassen, was seit längerem bekannt ist (siehe zum Beispiel Straka (1971)). Ein Körper knapp unter dieser Masse ist mit einer Oberflächentemperatur von etwa 2000 K aber immer noch eine glühende Gaskugel, die aufgrund ihres weit im Infraroten liegenden Strahlungsmaximums und ihrer geringen Leuchtkraft als brauner Zwerg bezeichnet wird.

Setzt man den zentralen Gravitationsdruck mit dem Strahlungsdruck gleich, so ergibt sich:

T_{c}(p_{S})=\left({\frac {9}{8\pi }}{\frac {G}{a}}\right)^{1/4}{\frac {\sqrt {M}}{R}}

In der Sonne wäre nach der elementaren Theorie eine Zentraltemperatur von 27,0 × 10⁶ K erforderlich, um der Gravitation nur mit dem Strahlungsdruck standzuhalten; tatsächlich sind es sogar 99,6 × 10⁶ K. Dies zeigt, dass bei einem solch massearmen Stern der Gasdruck weit überwiegt. Aufgrund des raschen Anstiegs des Strahlungsdrucks mit der Temperatur beginnt dieser ab einer bestimmten Masse $M_{S}$ aber zu dominieren. Die elementare Theorie liefert durch Gleichsetzen von Gas- und Strahlungsdruck bei identischer Zentraltemperatur:

M_{S}={\sqrt {\frac {18}{\pi aG^{3}}}}\left({\frac {k}{\mu }}\right)^{2}

Das Einsetzen der Konstanten liefert für $M_{S}$ einen Wert von 8,6 Sonnenmassen. Die elementare Theorie unterschätzt jedoch den zentralen Gravitationsdruck beinahe um den Faktor 200 und damit die Zentraltemperatur, bei der Gas- und Strahlungsdruck gleich sind, fast um den Faktor 4 (vierte Wurzel von 200). Dementsprechend liegt die Grenzmasse in Wahrheit um ebendiesen Faktor höher.

Aus der Proportionalität

T_{c}(p_{S})\propto {\frac {\sqrt {M}}{R}}

geht hervor, dass bei einem durch den Strahlungsdruck dominierten Stern die Zentraltemperatur nur noch mit der Quadratwurzel der Masse wächst. Wegen der sehr starken Temperaturabhängigkeit genügt bereits ein kleiner Temperaturanstieg, um zusätzlicher Gravitation standzuhalten, ja diese sogar zu überspielen. Der enorme Strahlungsdruck ist ein entscheidender Motor für Instabilitäten in massereichen Sternen, für deren bedeutenden Masseverlust im Verlauf ihrer Entwicklung. Inwieweit dadurch eine Obergrenze für die Masse eines Sterns festgelegt wird, ist noch immer nicht geklärt. Neuere Arbeiten (zum Beispiel Weidner und Kroupa (2004) oder Figer (2005)) legen nahe, dass diese Grenze bei etwa 150 Sonnenmassen liegen dürfte.

Zuletzt sei auch auf die Temperatur das Sonnenmodell von Abraham und Iben (1971) angewandt. Sie fällt mit zunehmendem Abstand vom Zentrum nicht so rasch ab wie die Dichte oder der Druck, vom Sonnenzentrum bis zu einem Abstand von 0,5 Sonnenradien von demselben ändert sich die Temperatur nur etwa um den Faktor 4. Durch die Division von Druck und Dichte in der Zustandsgleichung heben sich deren steile Gradienten zum Teil gegenseitig auf.

Energiefreisetzung

In den obigen Abschnitten wurde ad hoc ein Dichtegesetz $\rho (r)$ angenommen und daraus eine Schichtung für den Druck $p(r)$ und die Temperatur $T(r)$ abgeleitet. Tatsächlich folgt die Temperaturschichtung aus den Mechanismen der Energiefreisetzung und des -transports im Sterninneren und daraus mit Hilfe der Zustandsgleichung, der hydrostatischen Grundgleichung und Masseerhaltung die Druck- und Dichteschichtung.

Kontinuitätsgleichung der Leuchtkraft

Indem man die Energiefreisetzung pro Masse $\epsilon (r)$ in einer kugelförmigen Schale betrachtet, erhält man die Kontinuitätsgleichung der Leuchtkraft $L(r)$ :

{\frac {\mathrm {d} L(r)}{\mathrm {d} r}}=4\pi r^{2}\rho (r)\epsilon (r)

Sie ist mit den anderen Grundgleichungen gekoppelt, weil $\epsilon (r)$ wiederum von der Dichte und Temperatur abhängt. Um diese Abhängigkeit zu klären, muss der Mechanismus der Energiefreisetzung diskutiert werden. Während in der Phase der Sternentstehung lediglich potentielle Energie des Gravitationsfeldes frei wird, dominiert bei einem fertigen Hauptreihenstern das Wasserstoffbrennen (die Energiequelle ist hier der Massendefekt). Hierbei sind wiederum zwei verschiedene Mechanismen tätig, die Proton-Proton-Reaktion und der Bethe-Weizsäcker-Zyklus. Beide Reaktionen werden in den entsprechenden Artikeln ausführlich erläutert, so dass hier nur die wichtigsten, für die Bedingungen im Sterninneren relevanten Informationen zusammengestellt werden.

Proton-Proton-Reaktion

Auf verschiedenen Wegen werden dabei effektiv vier Protonen und zwei Elektronen zu einem Heliumkern und zwei Neutrinos. Die geschwindigkeitsbestimmende Startreaktion ist jeweils das Verschmelzen zweier Protonen zu einem Deuteriumkern (²H), wobei auch ein Positron und ein Neutrino gebildet werden. Das Positron zerstrahlt mit einem Elektron, das Neutrino verlässt den Stern direkt. ²H lagert rasch ein weiteres Proton an. Das entstehende ³He reagiert entweder mit einem weiteren ³He zu ⁴He, wobei zwei Protonen wieder frei werden. Alternativ kann es mit einem Proton und einem Elektron ein ⁴He und ein Neutrino bilden. Diese Reaktion ist nicht elementar, sondern durch ein schon früher gebildetes ⁴He katalysiert. Das Elektron wird entweder vor dem Zerfall des schweren Übergangskerns eingefangen oder zerstrahlt mit dem beim Zerfall freigesetzten Positron. Auf jedem dieser drei Reaktionswege werden pro gebildetem ⁴He 26,46 MeV Energie frei. Allerdings tragen die Neutrinos verschiedene Energiebeträge fort. Netto verbleiben 26,2, 19,3 bzw. 25,7 MeV.

Da bei der Startreaktion zwei Teilchen zusammentreffen müssen, ist deren Rate proportional zum Quadrat der Protonenkonzentration. Solange im Kern des Sterns hauptsächlich Protonen zur Masse beitragen, ist die Energiefreisetzung pro Masse direkt proportional zur Dichte. Die Abhängigkeit von der Temperatur kann nicht elementar begründet werden, nach Fowler (1967) ist $\epsilon (r)$ direkt proportional zu T⁴. Dieser Zusammenhang wird auch heute noch als korrekt angesehen (siehe zum Beispiel Brosch (2008)). Insgesamt gilt also:

\epsilon (r)\propto \rho (r)T^{4}(r)

Bethe-Weizsäcker-Zyklus

Diese Reaktion beginnt mit einem ¹²C-Kern, an den sich ein Proton anlagert. Der dabei entstehende ¹³N-Kern wandelt sich durch Beta-Zerfall in einen ¹³C-Kern um. Durch sukzessives Verschmelzen mit weiteren Protonen entstehen nacheinander die Kerne ¹⁴N und ¹⁵O. Aus letzterem entsteht durch einen weiteren Beta-Zerfall ¹⁵N. Durch erneutes Anlagern eines Protons entstehen schließlich die Kerne ¹²C und ⁴He. Am Ende liegt also wieder ein Kohlenstoffkern vor, während wiederum aus vier Protonen ein Heliumkern entstanden ist. Unter Berücksichtigung der Neutrinoverluste liefert die Reaktionskette 25,0 MeV. Wegen der Beteiligung der Elemente Kohlenstoff (C), Stickstoff (N) und Sauerstoff (O) wird diese Kette auch als CNO-Zyklus bezeichnet.

Da wie bei der Proton-Proton-Reaktion jeweils nur zwei Teilchen zusammentreffen, ist $\epsilon (r)$ abermals der Dichte direkt proportional. Die Temperaturabhängigkeit ist jedoch nun enorm, wobei der genaue Zusammenhang lange ungeklärt blieb. Fowler (1967) gab eine Proportionalität zu T²⁴ an, nach neueren Untersuchungen liegt laut Brosch (2008) ein etwas flacherer Anstieg mit ungefähr T¹⁵ vor. Somit ist:[2]

\epsilon (r)\propto \rho (r)T^{15}(r)

Die Temperatur, von der an die Energiefreisetzung durch den CNO-Zyklus gegenüber der Proton-Proton-Reaktion dominiert, liegt etwa bei 18 × 10⁶ K, was der Zentraltemperatur eines Sterns von etwa 1,1 Sonnenmassen entspricht.

Schlussfolgerungen

Wie bereits erläutert, steigt die Zentraltemperatur mit der Sternmasse. Dies hat wegen der starken Temperaturabhängigkeit der nuklearen Reaktionen einen enormen Anstieg der zentralen Energieproduktion $\epsilon _{c}$ zur Folge, insbesondere im Falle des CNO-Zyklus. Da die Temperatur nach außen hin abnimmt, geht aber auch die Energiefreisetzung mit wachsendem Abstand von der Sternmitte rasch praktisch auf Null zurück. Besonders steil ist dieser Rückgang für den CNO-Zyklus. Die Energie eines Sterns wird also fast vollständig in einem sehr kleinen Bruchteil seines Volumens in der Kernzone freigesetzt.

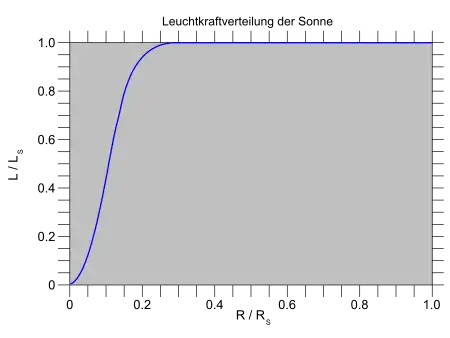
Das Sonnenmodell von Abraham und Iben (1971) bestätigt die qualitative Diskussion. Bis zu einem Abstand von nur 1/10 des Sonnenradius vom Zentrum, d. h. innerhalb von nur 1/1000 des Sonnenvolumens, wird schon die Hälfte der Leistung erbracht, bis zu 1/4 des Radius sind es 99 %. Der Sonnenreaktor besteht also aus einem kleinen brennenden Kern unter einer enorm dicken Hülle, welche die Energie einschließt, indem sie die Strahlung an einer geradlinigen Ausbreitung hindert. Man spricht von Strahlungsdiffusion.

Energietransport

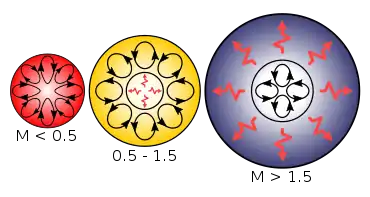
Mit der Dichte nimmt auch die Diffusionskonstante steil nach außen hin ab. Umgekehrt nimmt außerhalb des brennenden Kerns die Flächenleistungsdichte quadratisch mit dem Radius zu. Beides trägt zu einem steilen Temperaturgefälle bei. Im Falle des CNO-Zyklus – d. h. bei Sternen mit mehr als etwa 1,5 Sonnenmassen – ist dieser Gradient um den sehr kleinen Kern herum steiler als der adiabatische Temperaturgradient, sodass die Schichtung instabil wird (s. u.) und Konvektion eintritt. Dominiert die Proton-Proton-Reaktion – d. h. in massearmen Sternen – erfolgt aufgrund des flacheren Temperaturverlaufs der Energietransport im Innern nur durch Strahlung. Bei entarteter Materie, wie sie z. B. in einem weißen Zwerg vorliegt, muss auch die Wärmeleitung beachtet werden.

Transport durch Strahlung

In diesem Fall hängt das im Abstand $r$ vom Zentrum vorliegende Temperaturgefälle von der lokalen Leuchtkraft $L(r)$ und dem sogenannten Strahlungsleitvermögen $K(r)$ ab.

{\frac {\mathrm {d} T}{\mathrm {d} r}}=-{\frac {1}{K(r)}}{\frac {L(r)}{4\pi r^{2}}}

Das Strahlungsleitvermögen gibt an, wie viel Energie pro Weglänge durch Strahlung transportiert werden kann, wenn entlang dieses Weges eine gewisse Temperaturdifferenz vorhanden ist. Wie alle Materialeigenschaften erfordert auch $K(r)$ die Kenntnis der Temperatur und der Dichte.

K(r)={\frac {4ca(T(r))^{3}}{3\kappa (r)\rho (r)}}

c ist die Lichtgeschwindigkeit, a die bereits im Zusammenhang mit dem Strahlungsdruck genannte Konstante. $\kappa (r)$ bezeichnet die über alle Frequenzen gemittelte Opazität. Sie gibt an, wie viel der erzeugten Energie pro Weglänge auf dem Transport nach außen wieder absorbiert wird, ist also ein Maß für die Durchsichtigkeit der Materie. Je undurchsichtiger diese ist (je größer also die Opazität), umso geringer ist ihr Vermögen, Energie durch Strahlung nach außen abzuführen, und umso größer damit das sich ausbildende Temperaturgefälle. Die Bestimmung von $\kappa$ ist vor allem für die Außenschichten kühler Sterne extrem aufwendig, sie erfordert eine detaillierte Kenntnis der atomaren und molekularen Energieniveaus. Das Einsetzen von $K(r)$ liefert

Konvektionszonen in Hauptreihensternen verschiedener Masse (in Sonnenmassen). Rote Blitze stellen den Energietransport nur durch Strahlung dar, Ovale mit Pfeilen die Konvektion.

{\frac {\mathrm {d} T}{\mathrm {d} r}}=-{\frac {3\kappa (r)\rho (r)}{4ca(T(r))^{3}}}{\frac {L(r)}{4\pi r^{2}}}

.

Stabilität der Schichtung

Die Grenze für den Temperaturgradienten, ab der Konvektion einsetzt, ist durch den adiabatischen Temperaturgradienten gegeben. Für ein einatomiges ideales Gas gilt

{\frac {\mathrm {d} T}{\mathrm {d} r}}=\left(1-{\frac {1}{\gamma }}\right){\frac {T}{p}}{\frac {\mathrm {d} p}{\mathrm {d} r}},

wobei $\gamma =c_{p}/c_{v}$ den adiabatischen Index darstellt, das Verhältnis der spezifischen Wärmekapazitäten bei konstantem Druck und konstantem Volumen. Für ein vollständig ionisiertes ideales Gas gilt $\gamma =5/3$ .

Intensität der Konvektion

Die Intensität der Konvektion zu bestimmen ist eines der schwierigsten Probleme der Physik überhaupt, nicht nur der Stellarastronomie, und entzieht sich einer elementaren mathematischen Beschreibung. Die Schwierigkeit besteht darin, dass zusätzlich zum Energietransport auch ein Massentransport auftritt. Heiße, im Vergleich zu ihrer Umgebung „leichtere“ Materie steigt in kühlere Schichten auf und gibt dort Wärme ab. Umgekehrt sinkt kühle, gegenüber ihrer Umgebung schwerere Materie in wärmere Schichten ab und nimmt dort Energie auf. Eine in der Praxis oft benutzte heuristische Beschreibung liefert die Mischungswegtheorie. Diese betrachtet das Gas in einem Stern als eine Ansammlung diskreter Elemente, die über eine charakteristische Strecke, den sogenannten Mischungsweg, die Zustandsgrößen (Temperatur, Dichte und Druck) ihrer ursprünglichen Umgebung näherungsweise beibehalten. Eine Beschreibung dieses Modells findet sich beispielsweise bei Hansen u. a. (2004).

Durch Konvektion bilden sich oft großräumige Strömungen aus, die einen Stern erheblich durchmischen können. Schwere Elemente, die durch höhere Kernfusionsreaktionen im Überriesenstadium entstehen, können auf diese Weise bis an die Oberfläche gelangen. Ein Beispiel hierfür sind die Kohlenstoffsterne. Diese kühlen Riesen enthalten überdurchschnittlich viel Kohlenstoff in ihrer Photosphäre, der vom heliumbrennenden Kern bis ganz nach oben gelangt ist.

Auf der Sonne lässt sich die Konvektion ganz anschaulich beobachten. Die aufsteigenden Gasblasen sind für das wabernde Aussehen ihrer Oberfläche verantwortlich, was man durchaus mit dem Brodeln in einem Kochtopf vergleichen kann.

Masse-Leuchtkraft-Beziehung

Aus obiger Strahlungstransportgleichung kann man mittels der folgenden Abschätzung eine der grundlegendsten Beziehungen der Sternphysik ableiten. Über den ganzen Stern betrachtet ist das mittlere Temperaturgefälle vom Zentrum bis zur Oberfläche gleich $T_{c}/R$ , wobei $T_{c}$ die schon unter dem Abschnitt Zustandsgleichung diskutierte Zentraltemperatur ist. Näherungsweise gilt

{\frac {T_{c}}{R}}\approx -{\frac {3\kappa \rho _{c}}{4caT_{c}^{3}}}{\frac {L}{4\pi R^{2}}}

Damit ergibt sich für die Gesamtleuchtkraft $L$ des Sterns folgende Proportionalität

L\propto {\frac {T_{c}^{4}R}{\rho _{c}}}

Setzt man die schon bekannten Zusammenhänge $T_{c}\propto M/R$ (in durch Strahlungstransport dominierten Sternen überwiegt der Gasdruck gegenüber dem Strahlungsdruck) und $\rho _{c}\propto M/R^{3}$ ein, erhält man die klassische, bereits von Eddington abgeleitete Beziehung

L\propto M^{3}.

Die Masse-Leuchtkraft-Beziehung gestattet einige weitere fundamentale Schlussfolgerungen. Die Lebensdauer $t_{\text{nuklear}}$ eines Sterns kann man näherungsweise als proportional zu seinem Wasserstoffvorrat, also seiner Masse, und umgekehrt proportional zu seinem Wasserstoffverbrauch, also seiner Leuchtkraft ansetzen. Damit ist

t_{\text{nuklear}}\propto {\frac {1}{M^{2}}}.

Je massereicher ein Stern ist, umso kurzlebiger ist er! Während die Sonne etwa 10¹⁰ Jahre vom Wasserstoffbrennen zehren kann, muss ein Gigant der hundertfachen Sonnenmasse aufgrund seines etwa 10⁶-fachen Wasserstoffverbrauchs sich mit etwa 10⁶ Jahren bescheiden. Ein kleiner roter Zwerg mit 0,1 Sonnenmassen kann hingegen etwa 10¹² Jahre überdauern, da er mit 1/1000 des solaren Wasserstoffumsatzes auskommt.

Schließlich kann man auch einen Zusammenhang zwischen Masse und Oberflächentemperatur $T_{\text{ober}}$ herleiten. Nach dem Gesetz von Stefan-Boltzmann gilt

L\propto R^{2}T_{\text{ober}}^{4}

Gleichsetzen mit der Masse-Leuchtkraft-Beziehung liefert

T_{\text{ober}}\propto {\frac {M^{\frac {3}{4}}}{\sqrt {R}}}

Wie bei der Zentraltemperatur dominiert der Masseterm klar gegenüber dem Radiusterm. Das Verhältnis $M^{3/4}/R^{1/2}$ liegt bei einem M0-Stern bei 0,77, bei einem O5-Stern aber bei 5,43. Mit zunehmender Masse stellen sich höhere Oberflächentemperaturen ein, was angesichts der auch höheren Zentraltemperaturen freilich zu erwarten ist.

Die starke Zunahme der Leuchtkraft mit der Masse ist seit langem durch Beobachtungen von Doppelsternsystemen[3] gesichert, man sehe z. B. die großangelegte Untersuchung von Svechnikov und Bessonova (1984). Im Einzelfall ergeben sich dabei Abweichungen vom klassischen Gesetz. Dies ist vor allem darauf zurückzuführen, dass bei massereichen und auch sehr massearmen Hauptreihensternen der Energietransport im Kernbereich durch Konvektion erfolgt und nicht durch Strahlung. Die Zunahme der Oberflächentemperatur mit der Masse ist durch die Spektralklassifikation von Doppelsternen ebenfalls schon lange bekannt.

Masseverlust

Die bisherige Diskussion zeigt, dass die Masse der wichtigste Parameter eines Sterns ist und alle anderen Größen wie Leuchtkraft und Temperatur massiv beeinflusst. Schon eine Verringerung der Masse um 10 % im Laufe der Zeit muss daher signifikante Auswirkungen auf dessen Struktur haben.

Verlust durch Kernfusion

Tatsächlich verlieren alle Sterne Masse allein schon durch die Kernfusion. Ist die Leuchtkraft eines Sterns bekannt, kann man den Massenverlust mittels der Einsteinschen Masse-Energie-Äquivalenz E = m c² berechnen:

{\frac {\mathrm {d} M}{\mathrm {d} t}}={\frac {L}{c^{2}}}

Für die Sonne ist L = 3,85 × 10²⁶ J/s, woraus sich ein Masseverlust von 4,28 × 10⁶ Tonnen/s ergibt. Auf den ersten Blick scheint dies gewaltig zu sein, doch entspricht dies lediglich 6,79 × 10⁻¹⁴ Sonnenmassen pro Jahr. Verglichen mit der zu erwartenden Zeitskala des zentralen Wasserstoffbrennens von 10¹⁰ Jahren ist dieser Verlust also bedeutungslos. Für die massereichsten Hauptreihensterne beträgt der durch Kernfusion bewirkte Massenverlust nahezu 10⁻⁷ Sonnenmassen pro Jahr, was allerdings nur etwa einem Anteil von 10⁻⁹ der Sternmasse entspricht. Wieder ist die Zeitskala des Wasserstoffbrennens – nun etwa 10⁶ Jahre – zu kurz, als dass der nukleare Massenverlust signifikant auf den Stern rückwirken könnte.

Verlust durch Sternwind

Sterne verlieren Masse jedoch nicht nur durch Kernfusion, sondern auch durch unmittelbaren Auswurf von Materie, den sogenannten Sternwind. Eine Berechnung des daraus resultierenden Masseverlusts auf Grundlage theoretischer Modelle ist aufgrund der enormen Komplexität des Phänomens kaum möglich; man ist auf empirische Beobachtungsdaten angewiesen.

Im Fall der Sonne erlauben Satelliten und Raumsonden direkte Messungen des durch den Sonnenwind getragenen Partikelstroms. Diese Messungen zeigen, dass der Masseverlust mit etwa 10⁻¹⁴ Sonnenmassen pro Jahr in der gleichen Größenordnung wie der thermonukleare Massenverlust liegt, d. h. die Struktur der Sonne im Hauptreihenstadium ebenfalls nicht signifikant beeinflussen kann.

Bei allen anderen Sternen kann der Sternwind nur indirekt beobachtet werden, wobei jedoch in der Regel auch hier theoretische Modelle eingehen (siehe z. B. De Jager u. a. (1988)). Durch den Materieausfluss bildet sich um den Stern herum eine Gashülle und insbesondere bei kühlen Überriesen eine Staubhülle aus. Eine solche Gashülle verrät sich durch Emissionslinien, deren Profile eine Abschätzung der Gasdichte und Strömungsgeschwindigkeit (und damit des Masseverlusts) gestatten. Staubhüllen fallen dadurch auf, dass die von dem Stern ausgehende Infrarotstrahlung höher ist, als man anhand seiner Oberflächentemperatur erwarten würde. Der Überschuss erlaubt ebenfalls eine Abschätzung des Masseverlusts, wobei allerdings Annahmen über die Strömungsgeschwindigkeit gemacht werden müssen.

Bei massearmen Hauptreihensternen ist der Sternwind für einen solchen indirekten Nachweis zu schwach. Angesichts ihres sonnenähnlichen Aufbaus dürften auch ihre Massenverluste den solaren Verhältnissen entsprechen und damit für deren Entwicklung bedeutungslos sein. Bei sehr massereichen Hauptreihensternen – im Bereich der Spektralklasse O und z. T. auch noch B – kann der Masseverlust jedoch mehrere 10⁻⁶ Sonnenmassen pro Jahr erreichen und damit den nuklearen Masseverlust um 1–2 Größenordnungen übertreffen. Meynet u. a. (1994) (siehe auch unter Weblinks – Geneva Grids of Stellar Evolution Models) zeigten, dass ein solch starker Masseverlust in der Tat erhebliche Konsequenzen für die Entwicklung eines Sterns hat. So verlängert er dessen Lebensdauer, weil mit der sich verringernden Masse auch die Zentraltemperatur und damit die Kernreaktionsrate sinkt. Die Lebensdauer fällt weniger rasch mit der Anfangsmasse $M_{0}$ ab, als man nach der Masse-Leuchtkraft-Relation erwarten würde. Unter Umständen ist oberhalb von etwa 60 Sonnenmassen sogar ein Anstieg der Lebensdauer mit $M_{0}$ denkbar, weil der zunehmende Masseverlust den anfänglich höheren Wasserstoffumsatz überproportional stark zurückdrängt.

Extrem hohe Massenverluste fanden De Jager u. a. (1988) für einige gelbe Überriesen, die fast bis an 10⁻² Sonnenmassen pro Jahr heranreichen. Es ist auch ohne detaillierte Modellrechnungen einsichtig, dass ein so gewaltiger Materieauswurf schon in wenigen Jahrtausenden einschneidende Veränderungen der inneren Struktur des Sterns zur Folge hat.

Rotation

Besonders junge, heiße Sterne haben oft eine hohe Rotationsgeschwindigkeit. Die naheliegendste Folge ist eine Verringerung der Oberflächenschwere aufgrund der Fliehkraft. Damit geht ein verringerter Druck auf das Sterninnere und so dort eine niedrigere Temperatur einher. Dies zieht wiederum eine geringere nukleare Energieproduktion, d. h. Leuchtkraft nach sich. Ein rotierender Stern entspricht also einem nicht rotierenden mit geringerer Masse. Moderne Modellrechnungen, z. B. von Meynet und Maeder (1997), bestätigen diese qualitative Einschätzung. Sie zeigen aber auch, dass bei einem Hauptreihenstern die Leuchtkraft nur um wenige Prozent verringert wird, selbst wenn am Äquator die Fliehkraft nahe an die Gravitation heranreicht.

Die Rotation nimmt jedoch nicht nur Einfluss auf die Schwere, sondern auch auf die Dynamik der Sternmaterie. In rotierenden Sternen bilden sich Zirkulationsströmungen aus, die parallel zu den Längenkreisen verlaufen. Lange Zeit vertrat man die Ansicht, dass solche Strömungen nicht in Gebiete anderer chemischer Zusammensetzung eindringen können, insbesondere nicht in die Kernzone, wo sich die Produkte der Kernfusion anreichern. Durch Wechselwirkung mit den Konvektionsströmungen in den Kernen heißer Sterne ist Meynet und Maeder (1997) zufolge aber doch ein Übergreifen der Zirkulation auf die zentrale Sternregion möglich. Dies steht im Einklang mit Beobachtungen z. B. von Herrero u. a. (1992), die in den Spektren schnell rotierender O-Sterne einen ungewöhnlich hohen Anteil von Helium fanden. Dieses Helium könnte durch Zirkulation vom Kern bis an die Oberfläche gelangt sein.

Siehe auch

Weblinks

Sun Fact Sheet Zusammenstellung der Zustandsgrößen der Sonne
OPAL opacity code Datenbank mit Opazitäten für Sternmaterie verschiedener chemischer Zusammensetzung
Yellow CESAM code FORTRAN77 Quellcode einer Simulationssoftware für Sternaufbau und -entwicklung, Datenbank mit Entwicklungspfaden von Sternen unterschiedlicher Masse und chemischer Zusammensetzung im Hertzsprung-Russel-Diagramm.
EZ Stellar Evolution. (Nicht mehr online verfügbar.) Archiviert vom Original am 30. April 2007; abgerufen am 11. Mai 2013 (englisch). Auf FORTRAN95 basierende Simulationssoftware für Sternaufbau und -entwicklung, Datenbank mit Entwicklungspfaden von Sternen unterschiedlicher Masse und chemischer Zusammensetzung im Hertzsprung-Russel-Diagramm. Einzelne Entwicklungspfade können auch per Web-Interface erstellt werden.
Geneva Grids of Stellar Evolution Models Datenbank mit Entwicklungspfaden von Sternen unterschiedlicher Masse und chemischer Zusammensetzung im Hertzsprung-Russel-Diagramm, wobei z. T. auch die Rotation berücksichtigt wird.
BaSTI Datenbank mit Entwicklungspfaden von Sternen unterschiedlicher Masse und chemischer Zusammensetzung im Hertzsprung-Russel-Diagramm, wobei aufgrund verbesserter Opazitätstabellen vor allem das Riesenstadium genauer beschrieben wird als bisher.

Literatur

Z. Abraham, I. Iben: More Solar Models and Neutrino Fluxes. In: American Astronomical Society (Hrsg.): Astrophysical Journal. Nr. 170, 1971, S. 157.
N. Brosch: Sirius Matters. In: Springer Verlag (Hrsg.): Astrophysics and Space Science Library. 1. Auflage. Nr. 354, 2008, S. 150 ff.
D. F. Figer: An Upper Limit to the Masses of Stars. In: Nature Publishing Group (Hrsg.): Nature. Nr. 434, 2005, S. 192 ff.
W. A. Fowler: International Association of Geochemistry and Cosmochemistry. 1st Meeting. Hrsg.: International Association of Geochemistry and Cosmochemistry. 1967.
R. Kippenhahn, A. Weigert: Stellar Structure and Evolution. Hrsg.: Springer-Verlag. 1990.
C. J. Hansen, S. D. Kawaler, V. Trimble: Stellar Interiors: physical principles, structure and evolution, §§ 5.1, 7.1. Hrsg.: Springer. 2. Auflage. 2004, ISBN 0-387-20089-4.
A. Herrero, R. P. Kudritzki, J. M. Vilchez, D. Kunze, K. Butler, S. Haser: Intrinsic parameters of galactic luminous OB stars. In: Springer (Hrsg.): Astronomy and Astrophysics. Nr. 261, 1992, S. 209 ff.
C. De Jager, H. Nieuwenhuijzen, K. A. van der Hucht: Mass Loss Rates in the Hertzsprung-Russel Diagram. In: Springer (Hrsg.): Astronomy and Astrophysics Supplement. Nr. 72, 1988, S. 259 ff.
G. Meynet, A. Maeder, G. Schaller, D. Schaerer, C. Charbonnel: Grids of Massive Stars with High Mass Loss Rates (V.). In: Springer (Hrsg.): Astronomy and Astrophysics Supplement. Nr. 103, 1994, S. 97 ff.
G. Meynet, A. Maeder: Stellar Evolution with Rotation (I.). In: Springer (Hrsg.): Astronomy and Astrophysics. Nr. 321, 1997, S. 465 ff.
H. Scheffler, H. Elsässer: Physik der Sterne und der Sonne. Hrsg.: BI Wissenschaftsverlag. 2. Auflage. 1990, ISBN 3-411-14172-7.
K. Schwarzschild: Structure and Evolution of the Stars. Hrsg.: Princeton University Press. 1. Auflage. 1958.
M. A. Svechnikov, L. A. Bessonova: A Catalogue of Orbital Elements Masses and Luminosities of Close Double Stars. In: Centre de Donnees astronomiques de Strasbourg CDS (Hrsg.): CDS Bulletin. Nr. 26, 1984, S. 99 ff.
J. L. Tassoul: Stellar Rotation. Hrsg.: Cambridge University Press. 1. Auflage. 2000.
W. C. Straka: A Determination of the Lower Mass Limit for the Main Sequence. In: American Astronomical Society (Hrsg.): Astrophysical Journal. Nr. 165, 1971, S. 109 ff.
C. Weidner, P. Kroupa: Evidence for a Fundamental Stellar Upper Mass Limit from Clustered Star Formation. In: Wiley (Hrsg.): Monthly Notices of the Royal Astronomical Society. Nr. 348, 2004, S. 187 ff.
A. Weiss, W. Hillebrandt, H.-C. Thomas, H. Ritter: Cox and Giuli’s Principles of Stellar Structure. Hrsg.: Cambridge Scientific Publishers. 2004.
M. A. Zeilik, S. A. Gregory: Introductory Astronomy & Astrophysics, § 16.1–16.2. Hrsg.: Saunders College Publishing. 4. Auflage. 1998, ISBN 0-03-006228-4.

Einzelnachweise

A. S. Eddington: Sterne und Atome (Vorlesung 1925, aus dem Englischen von O. F. Bollnow), Vandenhoeck & Ruprecht, Göttingen 1955.
Carl J. Hansen u. a.: Stellar Interiors. (PDF; 9 MB), S. 23, Table 1.1.
Die Masse von Sternen ohne Begleiter ist, abgesehen von der Masse-Leuchtkraft-Beziehung, nicht bestimmbar.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] A. S. Eddington: Sterne und Atome (Vorlesung 1925, aus dem Englischen von O. F. Bollnow), Vandenhoeck & Ruprecht, Göttingen 1955.

[2] Carl J. Hansen u. a.: Stellar Interiors. (PDF; 9 MB), S. 23, Table 1.1.

[3] Die Masse von Sternen ohne Begleiter ist, abgesehen von der Masse-Leuchtkraft-Beziehung, nicht bestimmbar.