Sternoberfläche
Sterne haben als Gaskugeln keine feste Oberfläche. Dennoch wird – selbst in der astronomischen Fachliteratur – sehr oft der Ausdruck Sternoberfläche verwendet, und damit einhergehend Bezeichnungen wie Oberflächentemperatur, Oberflächenschwere und Sternradius. Da diese Größen sowohl für die Physik des Sterninneren (siehe Sternaufbau) als auch der äußeren Sternschichten fundamental sind, bedarf der Begriff der Sternoberfläche einer sehr sorgfältigen Definition.


In der astronomischen Beobachtungspraxis wird anstelle der Oberfläche in der Regel der Radius eines Sterns betrachtet, was aber zueinander äquivalent ist. Dementsprechend werden nach der Einleitung, welche zwei typische Beispiele von Sternoberflächen vorstellt, verschiedene Definitionen und Messverfahren für den Sternradius diskutiert.
Beispiele von Sternoberflächen
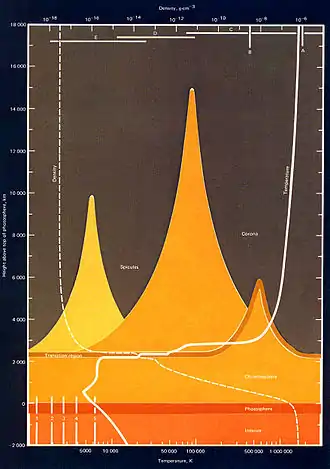
Oberfläche der Sonne
Als einziger Stern, dessen Oberfläche im Detail betrachtet werden kann, ist die Sonne bei weitem am geeignetsten, an die Problematik heranzuführen. Angesichts des vertrauten Bilds der scharf umrissenen Sonnenscheibe scheint bei unserem Zentralgestirn der Begriff Oberfläche trotz des Fehlens einer festen Kruste unproblematisch zu sein.
Beobachtet man aber die Sonne während einer totalen Sonnenfinsternis (oder mit einem das Licht der Sonnenscheibe weitgehend ausblendenden Instrument, einem sogenannten Koronografen), oder gar in anderen Wellenlängenbereichen, stellt man fest, dass sie an dem gewöhnlich so klar sichtbaren Rand keineswegs „aufhört“. Ohne das dominante Licht ihrer Scheibe erscheint die Sonne von einem weitausholenden, von Strahlen durchsetzten diffusen Kranz umgeben. Im Röntgenbereich bietet sich ein vergleichbares Bild, und auch im Radiobereich erscheint die Sonne wesentlich „größer“ als im sichtbaren Licht.
Dieses sehr komplexe Erscheinungsbild ist darauf zurückzuführen, dass die Außenschichten der Sonne aus mehreren Plasmaschichten bestehen, in denen sehr unterschiedliche physikalische Bedingungen herrschen. Dass unser Zentralgestirn im Sichtbaren einen scharfen Rand aufweist, ist dadurch zu erklären, dass die Photosphäre für elektromagnetische Wellen, Licht, tieferer Schichten undurchsichtig ist und in guter Näherung die Eigenschaften eines schwarzen Körpers besitzt, während alle Schichten oberhalb im sichtbaren Bereich so transparent sind, dass man meint, das sichtbare Licht würde einer dünnen Schicht entspringen, deren Dicke sehr klein ist im Vergleich zum Radius des eigentlichen Sonnenkörpers. Zudem ist die Photosphäre im Sichtbaren viel heller als die sich anschließenden Bereiche, die als Chromosphäre und Korona bezeichnet werden. Letztere sind wegen ihrer Lichtschwäche im Optischen nur sichtbar, wenn die sehr viel hellere, die Photosphäre repräsentierende Sonnenscheibe vom Mond oder künstlich abgedeckt wird.
Dass die Korona im Röntgenbereich nicht vom eigentlichen Sonnenkörper überstrahlt wird, hat sie ihrer sehr hohen Temperatur zu verdanken (bis zu 2 Millionen K gegenüber 4400–6600 K in der Photosphäre; siehe auch die Zusammenstellung der solaren Zustandsgrößen in dem unter Weblinks angegebenen NASA-Website Sun Fact Sheet). Die solare Radiostrahlung ist starken Schwankungen unterworfen. Neben einer ständig vorhandenen „ruhigen“ Strahlung treten im Rahmen von Sonneneruptionen, sogenannten Flares, immer wieder kurzzeitige heftige Strahlungsausbrüche auf.
Trotz des Bilds der klaren Sonnenscheibe bereitet die Definition des Begriffs Oberfläche also auch schon bei unserem Zentralgestirn erhebliche Schwierigkeiten. Da die Photosphäre im Vergleich zur Chromosphäre und Korona aber bei weitem den Löwenanteil der gesamten Leuchtkraft der Sonne stellt, scheint es ausreichend zu sein, die Oberfläche eines Sterns mit dessen Photosphäre gleichzusetzen.
Oberfläche von Beteigeuze

Jedoch gibt es Sterne, bei denen auch die Gleichsetzung Oberfläche = Photosphäre zu Schwierigkeiten führt. Dazu zählen beispielsweise Objekte wie Rote Riesen, Rote Überriesen, leuchtkräftige Blaue Veränderliche und Wolf-Rayet-Sterne. Detaillierte Untersuchungen zeigen, dass bei solchen Sternen die Dicke der Photosphäre nicht mehr klein gegenüber dem Radius des eigentlichen Sternkörpers ist.
Ein besonders intensiv untersuchter Stern mit ausgedehnter Photosphäre ist Beteigeuze. Trotz seiner Entfernung von 600 Lichtjahren kann seine Scheibe durch ihre gewaltige Größe noch als flächiges Objekt aufgelöst werden. Direkt möglich ist dies mit dem Hubble-Weltraumteleskop (siehe z. B. Gilliband und Dupree (1996)). Mit Hilfe der Apertursynthese (eine Erweiterung der klassischen Interferometrie, bei der nicht nur zwei, sondern mindestens drei Strahlenbündel zur Interferenz gebracht werden) oder des sogenannten Lucky Imaging kann Beteigeuze auch mit erdgebundenen Teleskopen wie dem in der Atacamawüste befindlichen Very Large Telescope als ausgedehnter Körper aufgelöst werden (siehe z. B. Haubois et al. (2009) oder Ohnaka et al. (2009)).
Wenn auch der Winkeldurchmesser von Beteigeuze nur etwa 5- bis 10-mal größer ist als die mittels der oben genannten Techniken erreichbare Winkelauflösung, so machen die mit dem Hubble-Weltraumteleskop oder dem VLT gewonnenen Aufnahmen doch den entscheidenden Unterschied zur Sonne deutlich. Die Scheibe von Beteigeuze hat keinen scharfen Rand, auch nicht in den Wellenlängenbereichen, in denen die Strahlung der Photosphäre dominiert. Zwar ist das diffuse Erscheinungsbild auch Folge der im Vergleich zum Winkeldurchmesser nach wie vor recht beschränkten Auflösung. Eine genaue Analyse der Atmosphäre Beteigeuzes bestätigt aber, dass der Eindruck einer im Vergleich zum eigentlichen Sternkörper ausgedehnten Hülle der Wahrheit entspricht.
Definitionen des Begriffs Sternradius
Die Unterschiede zwischen Sonne und Beteigeuze kann man auch durch folgendes Gedankenexperiment veranschaulichen. Könnte man in die Sonnenatmosphäre eindringen, so hätte man, solange man sich in der Korona oder Chromosphäre befände, noch eine weitgehend ungestörte Sicht nach außen, da diese Schichten nur einen geringen Anteil des sie durchquerenden Lichts absorbieren (und streuen). Nach dem Eintauchen in die Photosphäre aber würde man auf einer sehr kurzen Distanz von nur wenigen hundert Kilometern den Eindruck gewinnen, von einem gleißenden Nebel umgeben zu sein, da die nun zusätzlich über dem hypothetischen Sonnenreisenden sich befindlichen Schichten fast alles einfallende Licht absorbieren und streuen. Bei einem Eindringen in die Photosphäre Beteigeuzes würde die Sicht nach außen hingegen nur allmählich schlechter werden, man könnte noch mehrere zehn Millionen Kilometer zurücklegen, ehe sie sich völlig vernebelt.
Mit Hilfe der optischen Tiefe

Das hier skizzierte Gedankenexperiment gestattet eine erste Definition des Begriffs Sternradius. Er bezeichnet demzufolge denjenigen Abstand vom Sternmittelpunkt, bei dem die noch darüberliegenden Schichten einen gewissen Anteil des sie durchquerenden Lichts absorbieren.
Das Absorptionsverhalten von Sternatmosphären wird oft mittels der optischen Tiefe beschrieben. Hat eine Materieschicht die optische Tiefe , so lässt sie nur den Anteil e− des einfallenden Lichts passieren.
Leider führt der Versuch, mittels der optischen Tiefe zu einer objektiven Radiusdefinition zu gelangen, zu erheblichen Schwierigkeiten. Die erste Schwierigkeit besteht darin, den Wert der optischen Tiefe festzulegen, den die jenseits des Sternradius gelegenen Schichten aufweisen sollen. Meist wird = 1 gefordert, was bedeutet, dass die Außenschichten nur etwa 37 Prozent des sie durchquerenden Lichts passieren lassen. Oft wird aber auch die Festlegung = 2/3 benutzt, was einem Durchlassen von 51 Prozent der einfallenden Energie entspricht. Gerade bei Sternen mit ausgedehnten Atmosphären haben allein schon solche unterschiedlichen Definitionen erhebliche Konsequenzen. Bessell et al. zeigten schon 1989, dass bei sogenannten Mira-Sternen (veränderliche Rote Riesen mit sehr starken periodischen Helligkeitsschwankungen) die Radien sich um bis zu 10 Prozent unterscheiden, je nachdem ob für die Außenschichten = 1 oder = 2/3 gefordert wird.
Die zweite Schwierigkeit ergibt sich aus der Wellenlängenabhängigkeit der Absorption. Die dunkel erscheinenden Fraunhoferlinien des Sonnenspektrums zeigen anschaulich, dass die Photosphäre je nach Wellenlänge mehr oder weniger durchsichtig ist. In den Bereichen der Linien kann man nicht so tief in den Stern hineinschauen wie zwischen ihnen. Die hier diskutierte Definition liefert also einen größeren Radius, wenn man Wellenlängenbereiche benutzt, die von Spektrallinien belegt sind. Wieder sind Sterne mit ausgedehnten Atmosphären besonders betroffen. Bessell und seine Mitarbeiter (1989) fanden allein schon im sichtbaren Bereich für Mira-Sterne Radiusunterschiede von bis zu 100 Prozent je nach betrachteter Wellenlänge.
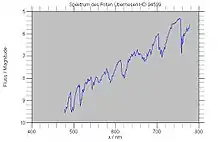
Erschwerend kommt bei Roten Riesen und Roten Überriesen hinzu, dass ihre Spektren praktisch keine linienfreien Bereiche haben. Wie das danebenstehende Beispiel von Malyuto et al. (1997) zeigt, werden im Sichtbaren die Spektren solcher Sterne von zahlreichen breiten Absorptionsbanden beherrscht, zwischen denen nur noch wenige schmale absorptionsarme Bereiche Platz finden.
Ein weiterer Nachteil der optischen Tiefe als Radiuskriterium ist ihre fehlende Handhabbarkeit. Das Absorptionsverhalten einer Sternatmosphäre lässt sich nicht unmittelbar messen, weil selbst in den linienfreien Bereichen noch kontinuierliche Absorption durch Streuung an freien Elektronen vorkommt, also ein absorptionsfreies Niveau nicht beobachtbar ist. Die Absorption kann man nur indirekt erschließen, indem man die von simulierten Modellatmosphären vorhergesagten Spektren mit dem beobachteten vergleicht.
Auf Grundlage der umschlossenen Masse
Will man ein Modell des inneren Aufbaus eines Sterns konstruieren (siehe Sternaufbau), so muss man festlegen, in welchem Abstand vom Sternmittelpunkt dieser „aufhören“ soll. Die optische Tiefe hier heranzuziehen ist problematisch, weil zwar im Sterninneren in guter Näherung lokales thermisches Gleichgewicht verwirklicht ist, nicht jedoch in den Außenschichten. Stattdessen wird häufig als Sternradius derjenige Abstand vom Mittelpunkt definiert, außerhalb dessen sich nur ein sehr kleiner Bruchteil der gesamten Sternmasse befindet, welcher Druck und Dichte der darunterliegenden Sternschichten nur noch marginal beeinflussen kann.
Auch diese Festlegung hat ihre Schattenseiten. Wie das unter Sternaufbau diskutierte Sonnenmodell zeigt, darf bei Hauptreihensternen der „außerhalb“ des eigentlichen Sternkörpers gelegene Massenanteil nicht zu groß angesetzt werden, weil bei solchen Sternen die Masse sehr stark zum Zentrum hin konzentriert ist. Lässt man bei der Sonne 1 Prozent der Gesamtmasse außer Acht (schließt man also 99 Prozent ihrer Masse innerhalb der Bezugsentfernung vom Mittelpunkt ein), so befindet man sich gemäß Abraham und Iben (1971) erst 0,82 Sonnenradien vom Zentrum entfernt, also noch weit unterhalb der Photosphäre! Detaillierte Untersuchungen von Baschek et al. (1991), welche das Sterninnere mit der Photosphäre verknüpfen, zeigen für Rote Riesen ein von der Sonne deutlich abweichendes Bild. Der Radius, welcher 99 Prozent der Sternmasse umgibt, ragt bereits in die Photosphäre hinein. Zwar haben Rote Riesen einen im Vergleich zur Sonne wesentlich dichteren Kern, die Masse der stark aufgeblähten Schichten ist aber weit weniger zum Zentrum hin konzentriert.
Hinsichtlich der Beobachtbarkeit ist der auf der umschlossenen Masse beruhende Radius als mindestens so kritisch zu betrachten wie der durch die optische Tiefe festgelegte. Wieder ist man auf Simulationen angewiesen, deren Vorhersagen mit der Beobachtung verglichen werden müssen.
Mit Hilfe der Temperatur
Die bisher besprochenen Radiusdefinitionen haben nicht nur den Nachteil, dass sie sich einer direkten Beobachtung entziehen. Da für die jenseits des Radius noch vorhandene Materie eine gewisse optische Tiefe bzw. Masse gefordert werden muss, haftet diesen Definitionen auch eine gewisse Willkür an. Die nun diskutierte Methode ist zumindest von diesem Mangel frei.
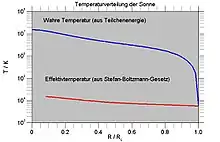
Modelle des Sterninneren geben nicht nur an, welche Masse mit zunehmender Entfernung vom Mittelpunkt umschlossen wird, sondern auch welche Leuchtkraft . Bei nicht pulsierenden Sternen ist außerhalb des Kerns die eingeschlossene Leuchtkraft konstant, die Energiestromdichte nimmt rein geometrisch mit dem Radius ab. Mittels des Stefan-Boltzmann-Gesetzes kann man die Energiestromdichte in die sogenannte Effektivtemperatur umrechnen, indem ungehinderte Abstrahlung der zugehörigen Schwarzkörperstrahlung angenommen wird. Im Sterninneren liegt die tatsächliche Temperatur (der Strahlung wie der Teilchen) viel höher, da dort das Strahlungsfeld entgegen der Annahme fast isotrop ist. An der Oberfläche fällt die Gastemperatur aber steil ab und schneidet schließlich die Effektivtemperatur (siehe Diagramm). Dieser Schnittpunkt definiert den Sternradius und die Oberflächentemperatur. Die Gastemperatur ist dort wohldefiniert, da die Teilchen (Elektronen, Ionen, Atome, Moleküle) untereinander noch weit über die Oberfläche hinaus durch Stöße lokal im Gleichgewicht sind.
Erneut stellt sich die Frage, inwieweit der so bestimmte Radius mit dem aus der optischen Tiefe konsistent ist. Für Hauptreihensterne trifft das tatsächlich zu. Bei Sternen mit ausgedehnten Atmosphären treten aber z. T. erhebliche Abweichungen auf, die nach Bessell und Mitarbeitern (1989) bis zu 40 Prozent ausmachen – die Temperatur liefert bei Roten Riesen systematisch größere Radien.
Auf Grundlage der Randverdunklung
Obige Aufnahme der Sonnenscheibe zeigt, dass sie in der Mitte wesentlich heller ist als am Rand. Diese sogenannte Randverdunklung ist darauf zurückzuführen, dass man im Zentrum der Sonnenscheibe in tiefere, d. h. heißere und damit nach dem Stefan-Boltzmann-Gesetz leuchtkräftigere Bereiche der Photosphäre hineinschauen kann als an ihrem Rand.
Die Randverdunklung kann ebenfalls zur Festlegung des Sternradius dienen. Als Radius gilt derjenige Abstand vom Sternmittelpunkt, bei dem die Intensität der Sternscheibe im Vergleich zur Mitte auf einen bestimmten Bruchteil abgefallen ist (in der Praxis wird er zumeist auf 1 Prozent gesetzt). Wie bei der optischen Tiefe und der umschlossenen Masse muss ein subjektiver Schwellwert definiert werden. Die Randverdunklung ist von allen Radiuskriterien jedoch das anschaulichste und spielt auch für praktische Radiusmessungen die weitaus bedeutendste Rolle. Die dabei auftretenden Schwierigkeiten werden zusammen mit den Messungen im nächsten Abschnitt behandelt.
Oberflächentemperatur

Die Oberflächentemperatur von Sternen ist die für uns messbare Temperatur des Sterns, sagt jedoch wenig über dessen innere Temperatur aus. Sie ist dort höher als die an der Oberfläche, weil im Inneren durch Kernfusion große Wärmemengen freigesetzt werden. Diese Wärme wird dann entlang des Temperaturgefälles nach außen transportiert und dort abgestrahlt, wobei die Beziehung zwischen der Wellenlänge des emittierten Lichtes und der Oberflächentemperatur des Sterns durch das Wiensche Verschiebungsgesetz gegeben ist.
Da man nicht in der Lage ist die Temperatur des Sterns direkt zu messen, wohl aber die Wellenlänge der von ihm freigesetzten Strahlung, kann man auf diese Weise die Oberflächentemperatur des Sterns indirekt ermitteln. Zum Beispiel hat die Sonnenstrahlung ein Spektrum mit einem Maximum bei 500 nm Wellenlänge (blau-grünes Licht), woraus sich eine Temperatur ihrer Photosphäre von ungefähr 5.800 Kelvin folgern lässt.
Messungen des Sternradius
Interferometrische Methode
Trotz ihrer großen Entfernungen sind Sterne keine Punktquellen. Interferometrische Techniken gestatten es, einen Stern als flächiges Objekt aufzulösen, d. h. insbesondere dessen Winkeldurchmesser zu bestimmen. Ist zusätzlich die Entfernung bekannt, kann aus dem Winkeldurchmesser unmittelbar der physische Radius abgeleitet werden. Im vergangenen Jahrhundert wurden mehrere interferometrische Verfahren entwickelt, die alle in den entsprechenden Artikeln erläutert werden, so dass hier nur eine kurze Zusammenfassung gegeben wird.
Verfahren
- Michelson-Sterninterferometer
- Hier werden durch zwei Primärteleskope im Abstand zwei Strahlenbündel erzeugt, die anschließend überlagert werden, so dass ein Interferenzmuster entsteht. Um den Winkeldurchmesser eines Sterns zu messen, beginnt man mit kleinem und zieht die Primärteleskope so lange auseinander, bis das Interferenzmuster verschwindet. Der Winkeldurchmesser ist dann direkt durch gegeben, wobei die verwendete Wellenlänge ist. Das Interferenzmuster wird erheblich durch die Luftunruhe gestört, so dass zur Erzielung einer hinreichenden Messgenauigkeit adaptive Optik eingesetzt werden muss.
- Intensitätsinterferometer
- In diesem Fall werden die beiden Primärstrahlen in Photoströme umgewandelt, die miteinander korreliert werden. Bei kleinem sind die Ströme stark miteinander korreliert. Mit zunehmendem wird die Korrelation immer geringer und sinkt schließlich auf Null ab. Je größer der Winkeldurchmesser eines Sterns, umso geringer ist der Abstand , der erforderlich ist, um einen Korrelationsabfall zu erzielen.
- Die Korrelation zwischen den Photoströmen ist aufgrund der Bose-Einstein-Statistik auf korrelierte Ankunftszeiten der Photonen zurückzuführen. In der Praxis wird sie von viel stärkeren, unkorrelierten Schwankungen der Ströme überlagert, die durch die Luftunruhe bedingt sind. Um sie wegzumitteln, sind sehr lange Belichtungszeiten (oft mehrere Tage!) erforderlich, so dass heutzutage dem mit adaptiver Optik ausgestatteten Michelson-Sterninterferometer aufgrund seiner weitaus besseren Empfindlichkeit der Vorzug gegeben wird.
- Speckle-Interferometrie
- Infolge der Luftunruhe erreicht das Licht eines Sterns auf leicht unterschiedlichen Wegen das Teleskop. Diese Pfade überlagern einander, so dass ein komplexes, aus einzelnen Flecken (englisch: Speckles) bestehendes Interferenzmuster entsteht, welches sich zudem ständig rasch ändert. Durch sehr kurze Belichtungszeiten (oft nur 1/100 Sekunde!) gewinnt man Interferenzmuster, welche näherungsweise als stationär betrachtet werden dürfen. Werden diese durch ein spezielles Verfahren miteinander kombiniert, entsteht ein rekonstruiertes Abbild des Sterns, welches fast allein der Beugung unterliegt, von der Luftunruhe aber weitestgehend frei ist. Nun ist die Empfindlichkeit durch kurze Belichtungszeiten beschränkt, so dass abermals moderne Michelson-Sterninterferometer besser abschneiden.
Probleme
- Randverdunklung
- Die Randverdunklung hat zur Folge, dass interferometrische Messungen generell einen zu kleinen Winkeldurchmesser liefern, da die bei der Mitte der Sternscheibe gelegenen Bereiche stärker zum Interferenzverhalten beitragen als diejenigen am Rand. So muss man im Vergleich zu einer gleichmäßig leuchtenden Scheibe bei dem Michelson-Sterninterferometer die beiden Primärteleskope etwas weiter auseinanderbringen, um das Interferenzmuster verschwinden zu lassen. Analoges gilt für das Intensitätsinterferometer, wo die Korrelation der beiden Photoströme etwas langsamer mit zunehmendem abfällt. Im Falle der Speckle-Interferometrie besteht die Gefahr, dass der Rand der Sternscheibe unter die Empfindlichkeitsgrenze des rekonstruierten Abbilds fällt.
- In der Praxis geschieht die Korrektur des gemessenen Winkeldurchmessers dadurch, dass man ihn mit einem Faktor multipliziert, welcher aus Modellen von Sternatmosphären abgeleitet werden muss. Glücklicherweise ist der Effekt selbst für einen Stern wie Beteigeuze trotz ausgedehnter Atmosphäre klein. So ermittelten Ohnaka et al. (2009) im nahen Infraroten für Beteigeuze einen nominellen Winkeldurchmesser von 43,2 Millibogensekunden und unter Beachtung der Randverdunklung von 43,6 Millibogensekunden. Der Unterschied von 0,4 Millibogensekunden entspricht also nur 1 Prozent des absoluten Winkeldurchmessers. Der Messfehler betrug für beide Werte weniger als 0,1 Millibogensekunden.
- Ausgedehnte Photosphäre
- Eine ausgedehnte Photosphäre lässt einen Stern größer erscheinen, als der darunterliegende eigentliche Sternkörper tatsächlich ist. Die Trennung der beiden Komponenten durch eine interferometrische Messung ist jedoch nicht möglich. Man ist auf Modelle sowohl der Sternatmosphäre als auch des Sterninneren angewiesen, wobei all die bereits im zweiten Abschnitt des Artikels diskutierten Unsicherheiten einfließen.
Genauigkeit
Der Winkeldurchmesser eines Sterns kann – einschließlich der Korrektur durch die Randverdunklung – mit modernen Interferometern mit einer extrem hohen Genauigkeit von unter 0,1 Millibogensekunden gemessen werden. Die Hauptfehlerquelle bei der Bestimmung des physischen Radius ist daher zumeist die Entfernung des Sterns. Für Objekte, welche einer interferometrischen Messung zugänglich sind, ist die Entfernung aber zumeist gut bekannt, da vom Hipparcos-Satelliten gemessene trigonometrische Parallaxen zur Verfügung stehen. Die Radien sind somit typischerweise von Unsicherheiten von nur wenigen Prozent des Absolutwertes behaftet.
Verfahren
Kennt man die Leuchtkraft und die Effektivtemperatur eines Sterns, so kann man nach dem Stefan-Boltzmann-Gesetz unmittelbar dessen Radius bestimmen:
Dieses Verfahren hat im Vergleich zur Interferometrie den Vorteil, dass es auch auf weit entfernte Sterne angewandt werden kann, deren Winkeldurchmesser zu klein für eine direkte Messung ist, z. B. auf Objekte im galaktischen Halo oder selbst nahen Nachbargalaxien wie den Magellanschen Wolken. Es sind somit Sterne zugänglich, die sich hinsichtlich ihrer chemischen Zusammensetzung erheblich von den Sternen der Sonnenumgebung, die in der Regel der galaktischen Scheibe angehören, unterscheiden. Auch können weit lichtschwächere Objekte wie Rote Zwerge oder gar Braune Zwerge untersucht werden.
Da nicht versucht wird, den Stern als flächiges Objekt darzustellen, ist zudem die Luftunruhe weit weniger störend als bei der Interferometrie, so dass keine adaptive Optik benötigt wird. Auch ist keine Kenntnis der Randverdunklung erforderlich.
Probleme
Den eben skizzierten Vorteilen stehen jedoch auch erhebliche Nachteile gegenüber. Um die Effektivtemperatur eines Sterns zu ermitteln, muss sein Spektrum aufgenommen und mit den Spektren simulierter Sternatmosphären verglichen werden. Die Radiusbestimmung mit Hilfe des Stefan-Boltzmann-Gesetzes ist also weit stärker von theoretischen Modellen abhängig als die interferometrische Methode, wo solche Modelle nur in die ohnehin kleine Korrektur der Randverdunklung eingehen.
Das zweite gravierende Handikap besteht darin, dass die Leuchtkraft des Sterns bekannt sein muss (weshalb von strahlungsenergetischer Methode gesprochen wird). Um sie zu bestimmen, muss die Intensität der Sternstrahlung über einen möglichst großen Wellenlängenbereich gemessen werden, wobei aber nicht nur die Entfernung des Sterns, sondern auch die Lichtschwächung durch den interstellaren Staub, die sogenannte interstellare Extinktion, bekannt sein muss. Sterne, bei denen die interferometrische Methode versagt, konnten in der Regel auch nicht von Hipparcos gemessen werden, so dass keine präzisen Entfernungsangaben vorliegen.
Bei erdgebundenen Beobachtungen ist es zudem gar nicht möglich, ein über alle relevanten Wellenlängenbereiche sich erstreckendes Spektrum zu gewinnen, denn sowohl der ultraviolette als auch der infrarote Anteil des Sternenlichts wird weitgehend von der Atmosphäre ausgefiltert. Sehr heiße und kühle Sterne (erstere strahlen überwiegend im Ultravioletten, letztere vor allem im Infraroten) sind davon besonders betroffen. Wieder ist man auf simulierte Sternatmosphären angewiesen, um von dem beobachteten Spektrum auf die ausgeblendeten Anteile schließen zu können.
Genauigkeit
Während die Effektivtemperatur in der Regel recht genau bestimmt werden kann (die Unsicherheit beträgt typischerweise nur wenige Prozent des Absolutwertes), ist die Leuchtkraft bei Sternen ohne eine von Hipparcos gemessene Parallaxe meist mit erheblicher Ungenauigkeit behaftet (die oft einige 10 Prozent des Absolutwertes ausmacht). Die mit Hilfe des Stefan-Boltzmann-Gesetzes ermittelten Radien sind also bestenfalls auf etwa 10 Prozent des Absolutwertes genau, d. h. dieses Verfahren steht hinsichtlich der Genauigkeit deutlich hinter der Interferometrie zurück. Wie schon im zweiten Abschnitt des Artikels gezeigt wurde, weicht zudem der auf der Temperatur beruhende Radius gerade bei Sternen mit ausgedehnten Photosphären deutlich von den anderen Radiusdefinitionen ab. Zum Vergleich der strahlungsenergetischen Radien mit den interferometrischen muss man erneut Modellatmosphären heranziehen.
Radiuswerte
Abschließend seien typische Werte für Sterne verschiedener Spektral- und Leuchtkraftklassen nach Scheffler und Elsässer (1990) zusammengestellt. Als Einheit wird der Sonnenradius verwendet.
| Spektraltyp | Hauptreihe | Riesen | Überriesen |
|---|---|---|---|
| O5 | 12,0 | – | – |
| B0 | 7,5 | 15 | 30 |
| A0 | 2,5 | 5 | 60 |
| F0 | 1,5 | 5 | 80 |
| G0 | 1,1 | 6 | 100 |
| K0 | 0,9 | 16 | 200 |
| M0 | 0,6 | 40 | 500 |
Siehe auch
Weblinks
- Sun Fact Sheet Zusammenstellung der Zustandsgrößen der Sonne
Literatur
- Abraham Z., I. Iben: More Solar Models and Neutrino Fluxes. In: American Astronomical Society (Hrsg.): Astrophysical Journal. Band 170, 1971, S. 157.
- B. Baschek, M. Scholz, R. Wehrse: The parameters R and in stellar models and observations. In: Astronomy and Astrophysics. Band 246, 1991, S. 374.
- M. S. Bessell, J. M. Brett, M. Scholz, P.R. Wood: The effects of photospheric extension upon the spectra of M type Mira variables. In: Astronomy and Astrophysics. Band 213, 1989, S. 209.
- R. L. Gilliland, A. K. Dupree: HST Imaging of Betelgeuse. In: International Astronomical Union Symposium. Band 176. Kluwer Academic Publishers, Dordrecht, 1996, S. 165.
- X. Haubois, G. Perrin, S. Lacour, T. Verhoelst, S. Meimon, L. Mugnier, E. Thiébaut, J.P. Berger, S.T. Ridgway, J.D. Monnier, R. Millan-Gabet, W. Traub: Imaging the spotty surface of Betelgeuse in the H band. In: Astronomy and Astrophysics. Band 505, 2009, S. 923 ff.
- V. Malyuto, M. O. Oestreicher, Th. Schmidt-Kaler: Quantitative Spectral Classification of Galactic Disk K-M Stars from Spectrophotometric Measurements. In: Monthly Notices of the Royal Astronomical Society. Band 286, 1997, S. 500.
- K. Ohnaka, K.-H. Hofmann, M. Benisty, A. Chelli, T. Driebe, F. Millour, R. Petrov, D. Schert, Ph. Stee, F. Vakili, G. Weigelt: Spatially resolving the inhomogeneous structure of the dynamical atmosphere of Betelgeuse with VLTI/AMBER. In: Astronomy and Astrophysics. Band 503, 2009, S. 183.
- Scheffler H., Elsässer H.: Physik der Sterne und der Sonne. Hrsg.: BI Wissenschaftsverlag. 2. Auflage. 1990, ISBN 3-411-14172-7, S. 122, auch S. 88–92.