Absolute Helligkeit

Die absolute Helligkeit ist eine Hilfsgröße in der Astronomie und Astrophysik, um die tatsächliche Helligkeit (somit bei selbstleuchtenden Objekten die Leuchtkraft) von Himmelsobjekten im sichtbaren Licht vergleichen zu können.

Definition

Die absolute Helligkeit unterscheidet sich von der scheinbaren Helligkeit, die man für ein Objekt von der Erde aus tatsächlich misst; letztere hängt zum einen von dessen Leuchtkraft (bei selbstleuchtenden Objekten wie Sternen) bzw. dessen Reflexionsvermögen (bei nicht selbstleuchtenden Objekten) und zum anderen von dessen Entfernung ab und wird bei Objekten außerhalb des Sonnensystems zusätzlich durch interstellare Materie beeinflusst.

Die absolute Helligkeit ist diejenige Helligkeit, die ein Beobachter aus einer einheitlichen Entfernung messen würde; diese ist wie folgt festgelegt:

für selbstleuchtende Objekte: 10 Parsec (32,6 Lichtjahre). Bei Sternen, die weniger als 10 Parsec entfernt sind, ist die scheinbare Helligkeit daher größer (d. h. ihr Zahlenwert kleiner) als die absolute Helligkeit und umgekehrt.
für reflektierende Objekte des Sonnensystems (Planeten, Kometen und Asteroiden): eine Astronomische Einheit (AE). Dabei wird angenommen, dass sich das Objekt 1 AE von der Sonne und zugleich 1 AE vom Beobachter entfernt befindet und in voller Opposition steht (also vom Ort der Sonne aus beobachtet wird).

Einheit und Größenordnung

Absolute Helligkeiten werden wie scheinbare Helligkeiten in Magnituden (mag) angegeben. Dabei bedeutet ein kleinerer Zahlenwert jeweils größere Leuchtkraft.

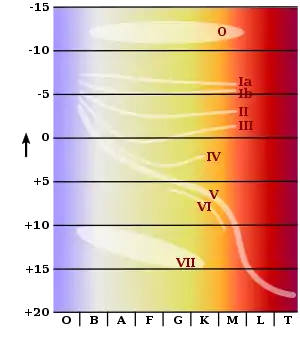
Die hellsten Fixsterne erreichen absolute Helligkeiten von etwa −9 mag (300.000-fache Leuchtkraft der Sonne), die lichtschwächsten dagegen +17 mag (weniger als ein Zehntausendstel der Sonnenleuchtkraft).

Insbesondere in älteren Werken zur Astronomie findet man häufig die Schreibweise mit einem hochgestellten M über dem Dezimalkomma, beispielsweise $3{\stackrel {\text{M}}{,}}0$ bei einem Stern der dritten (absoluten) Größenklasse. Die Verwendung des Großbuchstabens verdeutlicht dabei, dass es sich um eine absolute Helligkeit handelt.

Bolometrische Helligkeit

Die Bolometrische Helligkeit gibt die Helligkeit eines Sterns nicht nur im sichtbaren Licht, sondern im gesamten elektromagnetischen Spektrum an. Die hierfür erforderliche Korrektur hängt vom Empfindlichkeitsbereich des Messgerätes sowie vom Spektraltyp des betreffenden Objektes ab.

Die fotografische Helligkeit der Sonne (im sichtbaren Licht) beträgt $5{\stackrel {\text{M}}{\text{,}}}16$ , die bolometrische Helligkeit dagegen $4{\stackrel {\text{M}}{\text{,}}}74$ .

Entfernungsmodul

Die Differenz zwischen scheinbarer Helligkeit m und absoluter Helligkeit M wird Entfernungsmodul genannt, denn sie steht in festem Zusammenhang zur Entfernung r. Aus der Festlegung der Helligkeitsstufen folgt:

{\begin{aligned}{\frac {r}{10\,\mathrm {pc} }}&=10^{\frac {m-M}{5\,\mathrm {mag} }}\\\Leftrightarrow m-M&=5\,\mathrm {mag} \cdot \log _{10}\left({\frac {r}{10\,\mathrm {pc} }}\right)\end{aligned}}

Gibt man die Entfernungsmaßzahl $r^{*}=r/\mathrm {pc}$ als dimensionslose Zahl an, so lässt sich der Entfernungsmodul schreiben als:

{\begin{aligned}m-M&=5\,\mathrm {mag} \cdot (\lg r^{*}-\lg 10)\\&=-5\,\mathrm {mag} +5\,\mathrm {mag} \cdot \lg r^{*}\end{aligned}}

Aus der Definition der Parallaxensekunde folgt als Beziehung zwischen Entfernungsmaßzahl $r^{*}$ und jährlicher Parallaxe π (als dimensionslose Zahl in Bogensekunden):

r^{*}={\frac {1}{\pi }}

Damit ergibt sich dann:

{\begin{aligned}m-M&=-5\,\mathrm {mag} -5\,\mathrm {mag} \cdot \lg \pi \\&=-5\,\mathrm {mag} \cdot (1+\lg \pi )\\\Leftrightarrow \pi &=10^{{\frac {m-M}{-5\,\mathrm {mag} }}-1}\\\Leftrightarrow r^{*}&=10^{1-{\frac {m-M}{-5\,\mathrm {mag} }}}\end{aligned}}

Mit Hilfe dieser für die Astronomie wichtigen Formel kann für Sterne, deren Leuchtkraft bekannt ist (z. B. Cepheiden oder Supernovae vom Typ Ia), der Abstand berechnet werden, die Leuchtkraftentfernung. Auf diese Weise konnte 1923 die Entfernung des Andromedanebels ermittelt werden.

Zum Teil beruht der Unterschied zwischen scheinbarer und absoluter Helligkeit zusätzlich auf der interstellaren Extinktion, d. h. der teilweisen Absorption der Strahlung durch interstellaren Staub. Dies ist durch einen zusätzlichen Term, den Extinktionsparameter $A$ , in der Gleichung für den Helligkeitsunterschied zu berücksichtigen:

m-M=5\,\mathrm {mag} \cdot (\lg \,r^{*}-1)+A

m – M	Entfernung		m – M	Entfernung
m – M	Parsec	Lichtjahre	m – M	Parsec	Lichtjahre
−5	1,00	3,26	+5,5	125,89	410,61
−4	1,58	5,17	+6,0	158,49	516,93
−3	2,51	8,19	+6,5	199,53	650,78
−2	3,98	12,98	+7,0	251,19	819,28
−1	6,31	20,58	+7,5	316,23	1.031,41
00	10,00	32,62	+8,0	398,11	1.298,47
+1	15,85	51,69	+8,5	501,19	1.634,68
+2	25,12	81,93	+9,0	630,96	2.057,94
+3	39,81	129,85	+9,5	794,33	2.590,80
+4	63,10	205,79	+10,0	1.000,00	3.261,62
+5	100,00	326,16	+25,0	1.000.000,00	3.261.619,00

Beispiele

Hertzsprung-Russell-Diagramm

Absolute
Hellig-
keit
(mag)

Selbstleuchtende Objekte (Sterne)

Stern	Scheinbare Helligkeit (m)	Absolute Helligkeit (M)	Entfernungs- modul (m – M)	Entfernung
Sonne	−26,73 mag	0+4,84 mag	−31,57	1 AE
Sirius	0−1,46 mag	0+1,43 mag	0−2,89	002,64 pc
Wega	0+0,03 mag	0+0,58 mag	0−0,55	007,75 pc
Pollux	0+1,15 mag	0+1,08 mag	0+0,07	010,34 pc
Spica	0+1,04 mag	0−3,51 mag	0+4,55	081,30 pc
Rigel	0+0,12 mag	0−6,78 mag	0+6,90	240,00 pc
Deneb	0+1,25 mag	0−7,24 mag	0+8,49	499,00 pc

Reflektierende Objekte des Sonnensystems

Objekt	(Maximale) Scheinbare Helligkeit (m)[1]	Absolute Helligkeit (H)[1]	Entfernung zur Sonne
Venus	−04,9 mag	−04,4 mag	0,7 AE
Jupiter	−02,9 mag	−09,4 mag	4,9 – 5,5 AE
Eros	+07,0 mag	+11,2 mag	1,1 – 1,8 AE
Apophis	< +15,0 mag (Jahr 2029 bis zu +3 mag)	+19,7 mag	0,75 – 1,1 AE
Ceres	+06,6 mag	+03,3 mag	2,6 – 3,0 AE
Pluto	+13,7 mag	−00,8 mag	30 – 49 AE
Sedna	+21,0 mag	+01,5 mag	76 – ≈900 AE
2018 VG₁₈	+24,6 mag	+03,3 mag	aktuell 120 – 130 AE

Siehe auch

Literatur

Joachim Krautter et al.: Meyers Handbuch Weltall. 7. Auflage. Meyers Lexikonverlag, Mannheim / Leipzig / Wien / Zürich 1994, ISBN 3-411-07757-3, S. 237, 247 ff.
Arnold Hanslmeier: Einführung in Astronomie und Astrophysik. 2. Auflage. Spektrum akademischer Verlag, 2007, ISBN 978-3-8274-1846-3, S. 254 ff.

Einzelnachweise

Anthony Mallama, James L. Hilton: Computing apparent planetary magnitudes for The Astronomical Almanac. In: Astronomy and Computing. 25, October 2018, S. 10–24. bibcode:2018A&C....25...10M. doi:10.1016/j.ascom.2018.08.002.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Mallama_and_Hilton-1] Anthony Mallama, James L. Hilton: Computing apparent planetary magnitudes for The Astronomical Almanac. In: Astronomy and Computing. 25, October 2018, S. 10–24. bibcode:2018A&C....25...10M. doi:10.1016/j.ascom.2018.08.002.