Parallaxe
Als Parallaxe (von altgriechisch παράλλαξις parállaxis „Veränderung, Hin- und Herbewegen“)[1] bezeichnet man die scheinbare Änderung der Position eines Objektes, wenn der Beobachter seine eigene Position durch eigene Bewegungen verändert.
Definition als parallaktischer Winkel
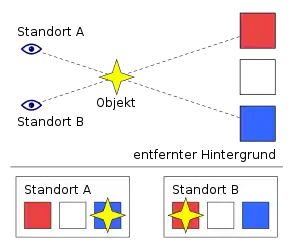
Definiert wird die Parallaxe als Winkel zwischen den Geraden, die von zwei verschiedenen Standorten auf denselben Punkt (ein Objekt) führen. Dies ist auch der Winkel, unter dem der Abstand der beiden Standorte, die „Basislinie“, erscheint, wenn sie vom beobachteten Objekt aus gesehen werden.
Hält man z. B. den Daumen aufwärts und betrachtet ihn abwechselnd mit dem linken und dem rechten Auge, so verschiebt sich sein Bild vor dem weiter entfernten Hintergrund. Die Basislinie ist hier der Augenabstand, die Methode heißt Daumensprung. Der parallaktische Winkel ist bei durchschnittlicher Armlänge etwa 6 Grad. Die Parallaxe ist umso größer, je näher sich das beobachtete Objekt befindet und je länger die Basislinie ist.
Das im Alltag kaum bewusste Phänomen der Parallaxe erlaubt die freiäugige Abschätzung von Entfernungen und ist die Grundlage des räumlichen Sehens. Bestimmt man die Parallaxe mit einem Sensor oder Messfernrohr und ist die Basislinie bekannt, lässt sich die Entfernung zum Zielpunkt genau berechnen. Dies wird u. a. beim Entfernungsmesser in Fotoapparaten angewandt, und mit höchster Messgenauigkeit in der Geodäsie und Astronomie.
Parallaxe in der Astronomie
Tägliche Parallaxe, Höhenparallaxe
Für Distanzmessungen zum Erdmond und nahen Planeten kann bereits der Erdradius als Basislinie dienen. So erscheint etwa die Parallaxe der Venus zwischen zwei Beobachtungsorten auf der Erdkugel in einer leicht verschiedenen Position vor dem Sternhintergrund. Bei den seltenen Venusdurchgängen vor der Sonne wurde die Parallaxe relativ zum Sonnenrand gemessen und brachte auf diese Weise erste Werte für den Radius der Erdbahn (die Astronomische Einheit).
Beim Mond beträgt die Parallaxe wegen seiner geringen Distanz maximal 2° (siehe Horizontalparallaxe), d. h. der Mond zieht z. B. von Europa aus betrachtet an völlig anderen Sternen vorbei als in Südafrika. Die Mondparallaxe ist auch verantwortlich für den verschiedenen Anblick, den eine Sonnenfinsternis von verschiedenen geographischen Breiten aus bietet. Man kann eine zu Hause nur partiell auftretende Finsternis nördlicher oder südlicher als totale Finsternis erleben. Wenn der Mondschatten die Erde in den Polregionen streift, findet dort prinzipiell nur eine partielle Finsternis statt. Für ein totales Finsterniserlebnis müsste der Sonnenfinsternistourist bereits ins Weltall reisen (die Mondparallaxe für sich künstlich vergrößern).
Ein zweites Messprinzip ist die Benutzung der Erdrotation: Auch von einem einzelnen Standort aus entsteht eine Parallaxe, weil der Ort allein durch die Drehung der Erde verschiedene Positionen erreicht. Die Anwendung dieses Effekts wird Höhenparallaxe genannt. Umgekehrt muss bei genauer Astrometrie dieser Einfluss auf die Messungen als Reduktion angebracht (korrigiert) werden.
Jährliche Parallaxe, Sternparallaxe
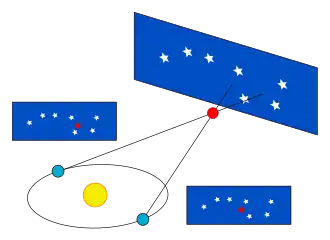
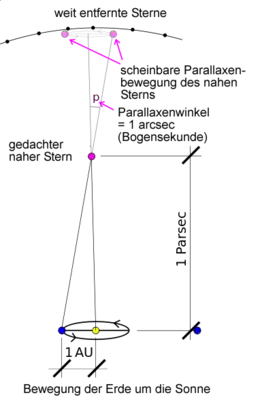
Die Parallaxe wird zur Entfernungsmessung sonnennaher Sterne eingesetzt. Als Basislinie dient der mittlere Radius der Erdbahn, der der großen Halbachse entspricht. Der Umlauf der Erde ändert die scheinbaren Sternpositionen in Form einer kleinen Ellipse, deren Form vom Winkel abhängt, um den der Stern von der Ekliptik (Ebene der Erdbahn) absteht. Die Parallaxe ist der Winkel, unter dem der Radius der Erdbahn vom Stern aus erscheint. Beträgt die Parallaxe eine Bogensekunde (1/3600 eines Grades), so entspricht das einer Entfernung von 3,26 Lichtjahren oder rund 31 Billionen Kilometern. Diese Entfernung wird auch als eine Parallaxensekunde (1 Parsec) bezeichnet.
Die Parallaxe ist selbst bei nahen Fixsternen so klein, dass man sie lange nicht beobachten konnte. Dies wurde in der frühen Neuzeit als wichtigstes wissenschaftliches Argument gegen das neue heliozentrische Weltbild ins Feld geführt. Auf der Suche nach der Parallaxe wurde zunächst ein völlig anderer Effekt, die Aberration, entdeckt. Erst 1838 gelang Friedrich Wilhelm Bessel die Parallaxenmessung: er wählte den Schnellläufer (Stern mit großer jährlicher Eigenbewegung) 61 Cygni aus und konnte die halbjährliche Winkeländerung nach längeren Analysen zu 0,31″ (0,00008 Grad) bestimmen[2]; der moderne Wert beträgt 0,29″. Selbst beim sonnennächsten Stern Proxima Centauri (4 Lichtjahre von der Erde entfernt) beträgt die Parallaxe nur 0,772″. In den 1990ern gelangen mit dem europäischen Astrometriesatelliten Hipparcos genaue Parallaxenmessungen für 118.000 Sterne. Der Nachfolger Gaia wurde im Dezember 2013 gestartet[3] und begann Anfang 2014 damit, noch vierzigmal genauere Messungen an etwa 1 Milliarde Sternen durchzuführen.
Sternstromparallaxe
Bei sich gemeinsam bewegenden Sternhaufen wie den Hyaden ist eine der Parallaxe verwandte, rein geometrische Entfernungsbestimmung möglich. Als Basislinie dient die über Jahre summierte Bewegung des Sternstroms. Dazu muss dessen Radialgeschwindigkeit und Eigenbewegung sowie der Konvergenzpunkt (Fluchtpunkt) am Himmel bekannt sein, dem die Haufensterne scheinbar zustreben.
Expansionsparallaxe
Bei astronomischen Objekten, die sich schnell ausdehnen, wie etwa planetarische Nebel und Supernovaüberreste, kann eine direkte Beobachtung dieser Ausdehnung zur Entfernungsbestimmung verwendet werden, indem aus einer Bestimmung der absoluten Ausdehnungsgeschwindigkeit (etwa durch Dopplerverschiebung) und der entsprechenden Winkeldistanz (der Expansionsparallaxe) auf die Entfernung geschlossen wird.
Ein ähnliches Verfahren wird zur Entfernungsbestimmung von Doppelsternen benutzt, die sowohl visuell als spektroskopisch sind, d. h. aus der visuellen Beobachtung der Bewegung erhält man einen Winkel und aus der Verschiebung der Spektrallinien eine absolute Geschwindigkeit, woraus dann die Entfernung berechnet wird.
Parallaxe im Sinne von Entfernung
Im älteren Sprachgebrauch der Astronomie wurde der Ausdruck Parallaxe auch für Entfernung bzw. Länge schlechthin benutzt, weil sich die Entfernung astronomischer Objekte in der Frühzeit der Astronomie nur auf der Grundlage der Parallaxe verlässlich ermitteln ließ. Dies galt auch dann, wenn die Entfernungsmessung andere – z. B. fotometrische – Verfahren nutzte.
Der Gebrauch von Parallaxe als Synonym für Entfernung ist darin erhalten, dass die Entfernung von Sternen in Parsec (pc, ca. 3,26 Lichtjahre), dem Kehrwert der halbjährlichen Parallaxe in Bogensekunden, angegeben wird. Parsec ist eine Abkürzung des englischen parallax arcsecond (‚Bogensekunde am parallaktischen Winkel‘).
Parallaxe in der Fotografie
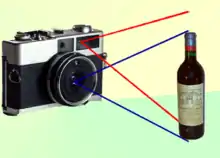 Parallaxefehler bei Sucherkameras, schematisch |
 Parallaxenmarkierungen in einem Leuchtrahmensucher |
In der Fotografie tritt bei zweiäugigen Kameras, sowohl bei Sucherkameras als auch zweiäugigen Spiegelreflexkameras, ein Parallaxenfehler auf: Der Bildausschnitt im Sucher und das resultierende fotografische Bild stimmen nicht überein. Dieser Fehler wird naturgemäß umso größer, je näher das Objekt gelegen ist. Einfache Kameras mit Leuchtrahmensucher haben oft eine zusätzliche, feststehende Markierung für den Nahbereich, aufwändigere Modelle besitzen einen automatischen Parallaxenausgleich: Die Entfernungseinstellung der Kamera dient nicht nur zur Fokussierung des Objektivs (Schärfe), sondern verändert auch den Winkel zwischen Sucher und Objektiv bzw. die Sucherfeldbegrenzung und kompensiert so den Großteil des Parallaxenfehlers. Frei von Parallaxenfehlern sind alle Kameras, die zur Erzeugung des Sucherbildes die gleiche Optik verwenden, die zur späteren Bildaufnahme verwendet wird.
In der Photogrammetrie (Bildmessung) dient die Parallaxe zwischen den Bildern von zwei Standorten als Maß für die Entfernung und wird mittels Stereoskopie ausgewertet. Als Vertikalparallaxe wird hingegen eine fehlerhafte Ausrichtung der Bilder bezeichnet, bei dem die Augenachsen in etwas verschiedene Höhen blicken müssen. Sie führt zu baldiger Ermüdung der Augen und sollte bewusst kontrolliert und weggestellt werden.
Parallaxe bei der Ablesung von Skalen

Bei genauen Messungen an Skalen – etwa an einem Zollstock oder einem Thermometer – muss die Ablesung senkrecht zur Skale erfolgen (Parallaxenfehler). Ein Spiegel hinter der Skala, wie er bei elektrischen Zeigermessgeräten häufig zu finden ist, erleichtert dies: Der Zeiger und sein Spiegelbild müssen zum Zeitpunkt der Ablesung in Deckung stehen.
Aber auch ohne Hilfsmittel kann die richtige Augenposition gefunden werden, wenn man auf die Skalenparallaxe achtet: der Mittelwert aus zwei Extrempositionen ist meist genauer als eine unkontrollierte Ablesung, wenn von einer linearen Skala abgelesen wird. Bei üblichen Außenthermometern kann man die Genauigkeit dadurch von 1 °C auf 0,5 °C verbessern.
Ausdehnungs- und Schleuderthermometer sind am genauesten ablesbar, wenn man sie senkrecht hängen lässt und beim Ablesen waagerecht blickt (wobei das Spiegelbild des eigenen Kopfes an einer Außenscheibe hilfreich sein kann).
Siehe auch
- Bewegungsparallaxe: Parallaxe aus Sicht der Wahrnehmung
Weblinks
- Wie misst man Entfernungen im All? Teil I aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 22. Okt. 2000.
- Wie misst man Entfernungen im All? Teil II aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 7. Jan. 2001.
- Wie misst man Entfernungen im All? Teil III aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 18. Feb. 2001.
Einzelnachweise
- Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. G. Freytag Verlag/Hölder-Pichler-Tempsky, München/Wien 1965.
- F. W. Bessel: Messung der Entfernung des 61. Sterns im Sternbilde des Schwans, in Populäre Vorlesungen über wiss. Gegenstände, Nr. VII, S. 208–268, Hrsg. H. Schumacher, Perthes & Besser, Hamburg 1848
- Arianespace successfully launches the Gaia scientific satellite. Arianespace, 19. Dezember 2013, abgerufen am 23. Februar 2016 (englisch).