Erdradius
Der Erdradius ist der Radius der als Kugel angenäherten Gestalt der Erde (Geoid), der „Erdkugel“. Er ist eine astronomische Maßeinheit und auch eine fundamentale Größe für viele Wissensgebiete – insbesondere für die Geowissenschaften – und für die Technik. Er beträgt im Mittel 6.371 Kilometer. Der Erddurchmesser ist das Doppelte des Erdradius, im Mittel rund 12.742 Kilometer.
Je nach Anwendungszweck werden verschiedene, genauere Erdradien verwendet, die nicht auf einer Kugelform, sondern auf der eines Rotationsellipsoids oder anderer Approximationen beruhen.
Häufig verwendete Werte
Da die Erde bzw. der Meeresspiegel (Geoid) keine exakte Kugelform besitzt, sondern an den Polen um je etwa 21 km (0,335 Prozent) abgeplattet ist, muss für genauere Angaben ihres Radius der Begriff „Erdkugel“ näher definiert werden. Am häufigsten werden folgende Werte verwendet:
- Äquatorradius RA = 6.378.137 m des mittleren Erdellipsoids (international festgelegter Wert der großen Halbachse a des GRS 80)
- Äquatorradius RA = 6.378.388 m des (älteren) Hayford-Ellipsoids von 1924
- Mittlerer Radius R0 = 6.371.000,785 m (volumengleiche Kugel, Kubikwurzel aus a·a·b, den Halbachsen des GRS 80-Ellipsoids)
- Gerundeter Wert R = 6.371,0 km zu oben, bzw.
- der ältere Wert 6.371,2 km (Hayford-Ellipsoid 1924)
- Arithmetisches Mittel R = (2a+b)/3 = 6.371.008,767 m bzw.
- flächengleiche Kugel 6.371.007,176 m (GRS 80-Ellipsoid)
Radien einiger wichtiger Erdellipsoide
| Ellipsoid | Jahr | Äquatorradius a | Polradius b | Mittelwert R0 |
|---|---|---|---|---|
| GRS 80, WGS 84 | 1979 | 6.378.137,0 m | 6.356.752,314 m | 6.371.000,8 m |
| WGS 72 | 1972 | 6.378.135,0 m | 6.356.750,5 m | 6.370.998,9 m |
| Internat. Ellipsoid | 1967 | 6.378.165,0 m | 6.356.779,702 m | 6.371.028,6 m |
| Hayford-Ellipsoid | 1910/24 | 6.378.388,0 m | 6.356.911,946 m | 6.371.221 m |
| Bessel-Ellipsoid | 1841 | 6.377.397,155 m | 6.356.078,962 m | 6.370.283 m |
| Peru/Lappland | 1740 | 6.379.500 m | 6.349.800 m | 6.369.600 m |
Geschichte
Von der Antike bis zu Kolumbus
Der Gedanke, dass die Erde kugelförmig sei, tauchte bereits um 600 v. Chr. in der ionischen Naturphilosophie auf (Thales von Milet, Anaximander) und im 4. Jahrhundert v. Chr. gab Aristoteles drei astronomische Beweise für diese Tatsache an.
Die erste Bestimmung des Erdumfangs ist von Eratosthenes (um 240 v. Chr.) überliefert, dem Erfinder der Gradmessungs-Methode. Er verglich die Winkelhöhen des Sonnenhöchststandes in Ägypten zwischen Alexandria und Syene (dem heutigen Assuan), die sich um 1/50 des Vollkreises unterscheiden. Hieraus ergab sich als Erdumfang das 50fache der Entfernung von Alexandria nach Assuan, nach heutigen Einheiten also 835 km mal 50 gleich 41.750 km. Aus dem Umfang kann der Radius rechnerisch abgeleitet werden. Eratosthenes rechnete in Stadien; für die Genauigkeit seiner Bestimmung des Erdradius spielt die verwendete Längeneinheit allerdings keine Rolle: Eratosthenes kam danach auf einen Erdradius von ca. 6.645 km und damit auf einen Wert, der 4,2 Prozent über dem heutigen liegt.
Im frühen Mittelalter ermittelten die Araber die Länge eines Grades zu 56 2/3 arabischen Meilen. Da diese mit ca. 2.000 m gleichzusetzen ist, ergibt sich der Radius des Erdkörpers R = 6.500 km, der 2 Prozent vom heutigen Wert abweicht. Der Mathematiker Al-Biruni ermittelte im Jahr 1023 mit einem von ihm erfundenen neuen Messverfahren den Radius der Erdkugel schließlich auf 6.339,6 km[1].
Im 15. Jahrhundert waren diese Werte in Europa sicherlich bekannt, doch wurde den arabischen Werten teilweise die um 25 Prozent kürzere italienische Meile zugewiesen. Auf dieser Basis und bei gleichzeitiger Überschätzung der Länge Asiens kam Kolumbus zu dem letztlich fehlerhaften Schluss, dass man auf Westkurs in wenigen Wochen nach Ostasien gelangen müsste.
Ferdinand Magellan begann im August 1519 eine Weltumsegelung. Als die Flotte 1520 die Philippinen und damit nachweislich asiatische Gewässer erreichte, war der endgültige Beweis für die Kugelgestalt der Erde erbracht, der lange Zeit zu gering geschätzte Erdumfang wurde nun richtig erkannt.
Erdmessung in der Neuzeit
Die tatsächliche Größe der Erde war erst am Ende der Entdeckerzeit auf einige Prozent genau bekannt. Ihre Abweichung von der Kugelform bestimmten französische Wissenschaftler des 17. Jahrhunderts durch Gradmessungen über einige hundert Kilometer, was aber noch unsicher war und teilweise sogar zu einem verlängerten Polradius führte. Demgegenüber berechnete Isaac Newton, dass die Erdrotation wegen der Trägheit (fälschlich: Fliehkraft) eine Abplattung der Erde verursachen müsse.
Die Klärung dieser Frage erfolgte durch die Erdmessung der französischen Akademie mit ihren zwei Expeditionen nach Lappland und Peru (1736 bis 1741). Sie dienten gleichzeitig zur Meter-Definition (postulierter Erdumfang über die Pole = 40.000 km) und erbrachte eine Genauigkeit von 0,02 Prozent oder 1,5 km (Meridianquadrant = 10.002.250 m, mittlerer Erdradius R0 = 6.369,6 km).
Seitdem hat sich die Genauigkeit, mit der die mathematische Erdfigur bekannt ist, zunächst alle 50 Jahre verdoppelt. Um 1965 bewirkte die Satellitengeodäsie eine enorme Genauigkeitssteigerung auf 20 Meter und stößt nun bereits in den Zentimeter-Bereich vor. Neu entwickelte Gradiometrie-Satelliten wie GRACE (2004) und GOCE zielen sogar auf die Änderungen der Erdfigur, die im Bereich von einigen Millimetern pro Jahr vermutet werden.
Regionale und örtliche Details der Erdgestalt
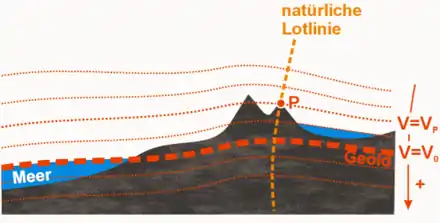
Die Abweichungen der Erde von der Kugelform wären zwar an einem idealen Globus noch nicht sichtbar, doch die Hochgebirge könnte man anhand ihrer „Rauigkeit“ ertasten. Die Erdabplattung (Abflachung an den Polen um 21 km oder 0,3 Prozent) muss hingegen in jeder genauen Landkarte berücksichtigt werden, oft auch der typische Verlauf der Erdkrümmung jedes Kontinents („Wellen“ im Geoid bis ±100 Meter). Der Krümmungsradius kann regional zwischen etwa 6.330 km und 6.400 km variieren, lokal sogar zwischen 5.000 und 8.000 km.
Insgesamt bedeutet die regionale Veränderlichkeit des Erdradius eine Änderung des Maßstabs von Karten und Rechenmodellen bis zu einigen Kilometern auf 1.000 km und ist in fast allen Anwendungen zu berücksichtigen. Bei der millimetergenauen Vermessung heutiger technischer Projekte wirken sich diese Effekte schon auf 100 Meter Distanz aus.
Die Höhenlage oder Form des Geländes wird hingegen nicht dem Erdradius zugeschlagen, sondern – etwa in Geoinformationssystemen – den Datenbanken als Attribut hinzugefügt. Bei Aufgabenstellungen mit physikalischem Hintergrund ist auch die Veränderlichkeit der Erdbeschleunigung zu berücksichtigen, die auf der Erdoberfläche global Werte von 9,76 bis 9,94 m/s² annimmt.
Bei Aufgabenstellungen der Astronomie oder der Raumfahrt wird häufig der Abstand eines Punktes vom Erdmittelpunkt benötigt, der sogenannte geozentrische Radius. Er lässt sich aus dem verwendeten Erdellipsoid berechnen und beträgt zum Beispiel in Mitteleuropa 6.365 bis 6.368 km, wozu noch die Meereshöhe des Punktes kommt. Davon ist jedoch der Krümmungsradius von Niveauflächen und bei Höhenmessungen zu unterscheiden, der bis 30 km größer sein kann.
Physikalische Einflüsse
Der Erdradius und seine Variation ist nicht nur eine fundamentale Größe bei geometrischen Aufgabenstellungen, sondern auch in der Physik und verschiedenen Geowissenschaften. Hier tritt er etwa als Abstand vom Erdzentrum oder von der Erdachse auf (R·cos(Breite)), als Krümmungsradius in Bewegungen oder bei Messstrahlen, als gaußsches Krümmungsmaß (1/R²) oder in der Wirkung von Gradienten verschiedener Kräfte.
Die mittlere Schwerkraft auf der Erdoberfläche hängt ebenso mit dem Radius und der Erdmasse zusammen wie die mittlere Dichte des Erdkörpers. Ihr Wert von 5,52 g/cm³ gibt der Geophysik – im Vergleich mit üblichen Gesteinsdichten von 2,5–2,8 g/cm³ – einen klaren Hinweis, dass die Dichte des Erdinneren wesentlich höher sein muss. Seit über 100 Jahren erforscht man den inneren Schalenaufbau der Erde unter anderem durch Gravimetrie, mathematische und seismische Modelle.
Resümee
Die genaue Erdfigur ist heute bereits auf wenige Zentimeter bekannt, obwohl ihr Höhenverlauf um 10 bis 15 km nach beiden Seiten variiert:
- mittlerer (volumengleicher) Erdradius = 6.371 km
- geozentrischer Mittelwert, Variation = 6.368 km ±11 km
- Halbachsen des Erdellipsoids = (äquatorial:) 6.378,1 bzw. (polar:) 6.356,7 km
- kontinentale Krümmungsradien (Nord-Süd) = (äquatorial:) 6.330 bis (polar:) 6.400 km
- „Erdkugel“ daher nur bis 0,5 % Genauigkeit ausreichend.
Vielfach ist unbekannt, dass wegen der Erdabplattung nicht nur der Erdradius variiert, sondern auch ein „Breitenproblem“ besteht: die geografischen und die geozentrischen Breiten unterscheiden sich um bis zu 0,19° oder 22 Kilometer. Wegen weiterer lokaler Abweichungen der Form der Erde von einer Kugel wurde daher für die Landesvermessung die Erdoberfläche durch lokal optimal passende Referenzellipsoide approximiert, von denen weltweit über hundert verschiedene in Gebrauch sind. Die Angabe von geografischen Koordinaten eines Ortes bezieht sich immer auf ein bestimmtes Bezugssystem (Geodätisches Datum).
Das bedeutet, dass ein unter unseren Füßen verlängert gedachtes Lot bis zu 20 km am Erdmittelpunkt vorbeigeht. Fachgebiete wie die Erdmessung, Geophysik und Satellitengeodäsie müssen sich täglich mit den damit zusammenhängenden Tatsachen auseinandersetzen.
Erdumfang
Wird für die Erdfigur näherungsweise eine Kugelform angenommen, kann der Erdumfang mittels der Umfangsberechnung für einen Kreis näherungsweise aus dem Erdradius berechnet werden: . Das ergibt bei einem Erdradius von 6.371 km einen Erdumfang von etwa 40.030 km.
Wegen der Erdabplattung ist der Umfang am Äquator mit etwa 40.075 km am größten. Der Abstand der Pole vom Äquator beträgt etwa 10.002 km, dies entspricht einem Erdumfang entlang eines Längenkreises von etwa 40.008 km. Dieser Wert liegt auffallend nahe bei dem runden Wert 40.000 km. Ursache ist, dass nach einer frühen Definition die Maßeinheit Meter als 10-millionster Teil eines Erdquadranten festgelegt werden sollte.[2]
Die Länge der Breitenkreise ist im Gegensatz zur Länge der Längenkreise nicht einheitlich und nimmt vom Äquator zu den Polen hin ab. Ihre Länge lässt sich bei Vernachlässigung der Erdabplattung näherungsweise berechnen zu , wobei die geografische Breite bedeutet. Die Länge des Mainz durchlaufenden 50. Breitenkreises beträgt demnach etwa .
Literatur
- Wolfgang Torge: Geodesy. 3. completely revised and extended edition, ISBN 3-11-017072-8. De Gruyter-Verlag, Berlin 2001
Einzelnachweise
- https://blogabissl.blogspot.com/2019/10/wie-biruni-1023-den-erdradius-auf-26.html abgerufen 19. Oktober 2019
- Ludwig Bergmann: Bergmann-Schaefer Lehrbuch der Experimentalphysik: Bd. 1. Mechanik, Akustik, Wärme. 10. Auflage. de Gruyter, Berlin 1990, S. 3