Schale (Technische Mechanik)
Eine Schale ist in der Technischen Mechanik ein Flächentragwerk, das gekrümmt ist und Belastungen sowohl senkrecht (wie eine Platte) als auch in seiner Ebene (wie eine Scheibe) aufnehmen kann (→Schalentheorie).
Schalen verdanken ihre Tragwirkung der Krümmung und Verdrehung. Sie können einfach gekrümmt sein, z. B. zylindrisch, oder doppelt gekrümmt, z. B. sphärisch.
Schalen nutzen die Tragfähigkeit ihres Materials optimal aus, indem sie Lasten über Membrankräfte abtragen, die über die Dicke der Schale konstant sind. So kommt es zu hoher Steifigkeit bei geringem Gewicht und Materialeinsatz, was die Schalen in Natur und Technik bedeutend macht.
In der Natur kommen Schalen vor in:
- Halmen von Süßgräsern
- Außenskeletten von Gliederfüßern (Insekten, Spinnen, Krebse) oder Schalenweichtieren (Muscheln)
- Vogeleierschalen
- Knochen (Schädel, Schulterblatt)
- Panzern (Schildkröten).
In der Technik und im Alltag finden sich Schalen in
- Silos
- Dachkonstruktionen (HP-Schalen), Betonschalen, Gewölben, Kuppeln
- Karosserien
- Gefäßen (Schalen, Dosen, Flaschen)
- Rohren
Definition
„Unter Schale versteht man in der Festigkeitslehre einen nach einer krummen Fläche gebildeten Körper, dessen Dicke im Verhältnis zu seiner übrigen Ausmaßen äußerst gering ist. Auch die Benennung „Schale“ weist darauf hin, dass es sich um einen Körper handelt, dessen Dicke verhältnismäßig ebenso klein ist wie die der Eierschale.“
Die Schalenbauweise ist eine Form einfach oder doppelt gekrümmter Flächentragwerke. Im Gegensatz dazu werden räumliche Flächentragwerke aus kraftschlüssig miteinander verbundenen ebenen Elementen (Scheiben) als Faltwerke bezeichnet. Die Lasten von Schalen werden – anders als beim herkömmlichen Bauen – durch Längskräfte und Biegung aufgenommen. Bei dünnen Schalen, deren Dicke klein gegenüber der Spannweite ist, kann die Biegung vernachlässigt werden; in diesem Falle werden die Lasten primär durch Längskräfte zu den Auflagern hin übertragen. Diesen Zustand bezeichnet man als Membranspannungszustand.
Gestalterische Aspekte
Schalen verbinden durch die geringe Stärke ihrer Wölbung den Vorteil einer selbsttragenden Membran mit großen Spannweiten.
Kuppelartige Wölbungen schaffen mehr nutzbaren Raum als konkave, nach innen gewölbte Krümmungen von Membran- und Seilnetzkonstruktionen. Der überwölbte Raum wirkt beschützend. Primäre Stützkonstruktionen, wie die Pylonen von Membrankonstruktionen, sind bei Schalentragwerken nicht notwendig, so dass ein ungestörtes Raumkontinuum gebildet werden kann. Da gekrümmte Gitterschalen mit annähernd beliebigen Projektionsflächen hergestellt werden können, stellen Übergänge und Anschlüsse an orthogonalen Flächen selten ein Problem dar. Kuppeln können beispielsweise auf einem kreisförmigen Grundriss und Tonnengewölbe auf einer rechteckigen Grundfläche errichtet werden.
Dünne Schalen sind leistungsfähig, aber auch empfindlich. Neben speziellen statisch-konstruktiven Eigenschaften können sie ebenso besondere ästhetische Ansprüche erfüllen.
Historie
Dieser Abschnitt beschäftigt sich bisher vor allem mit der Geschichte der Kuppeln, für die Geschichte von Gewölben siehe dort.
Die Analyse von Kuppeln und Schalen stellt eine Wechselbeziehung von Konstruktion und Form dar. Der Wunsch nach weiten, stützenlosen Raumüberdachungen war schon in der Antike ein beliebtes Thema, was zur damaligen Zeit bis in weiteren Entwicklungsstufen auf große technische Schwierigkeiten stieß.
In der Antike setzten sich als Bauform Kragkuppeln durch, bei denen die einzelnen Ringe auf ebenen Lagerfugen aufgesetzt wurden. In der späten Bronzezeit entstanden die mykenischen Kuppelgräber. Die Wände wurden aus monumentalen Steinquadern hergestellt. Als bedeutendes Beispiel hierfür ist das Schatzhaus des Atreus um etwa 1325 v. Chr. zu nennen. Bei diesem Bauwerk konnte damals bereits ein Durchmesser von 14,50 Metern und eine Höhe von 13,20 Metern erreicht werden. Es blieb bis zum Pantheon in Rom 1400 Jahre lang der größte Kreiskuppelbau.
Das Pantheon, 118 n. Chr. erbaut, besteht in der Konstruktion seiner Kuppel aus einer inneren und einer äußeren Schale aus Gussbeton. So konnte erstmals eine Spannweite von 43,30 Metern erreicht werden, die über 1400 Jahre unübertroffen blieb.
Erst mit der Einführung des Stahlbetons endete die lange Tradition der gemauerten Kuppeln. Erste kleine Eisenbeton-Kuppeln wurden im Monier-Verfahren hergestellt. Größere Kuppeln wurden rechnerisch und konstruktiv in Balken und Rippen zerlegt. Nach diesem Prinzip wurde die damals größte Kuppelkonstruktion der Jahrhunderthalle in Breslau 1911–1913 mit einer Spannweite von 65 Metern erbaut.
Die Zukunft im Kuppelbau gehörte jedoch den dünnwandigen Kuppelschalen. Es folgte ein Übergang zu dünnen, leichten Schalentragwerken. Ausschlaggebend für diese Entwicklung war sicher das kugelkalottenförmigen Zeiss-Planetarium in Jena. Durch die Entwicklung der Ferrozementbauweise Anfang der 1920er Jahre konnte man sehr schlanke Schalentragwerke erstellen. Als Beispiel hierzu ist die zweite Planetariumskuppel in Jena zu nennen. Sie besitzt bei einer Spannweite von 25 Metern eine Schalendicke von nur 6 Zentimetern. Die nach diesem Verfahren errichteten Kuppelschalen in den späten 1920er Jahren ermöglichten die Überwölbung immer größerer Räume.[1][2]
Einen großen Fortschritt auf dem Gebiet der Schalenbauweise und insbesondere die Verwendung der Schale als Dachkonstruktionen gab es nach dem Zweiten Weltkrieg. Vor dem Zweiten Weltkrieg kannte man die einfach gekrümmten Schalen, die hauptsächlich zu zylindrischen Schalen führten (Tonnengewölbe, Türme), und man kannte Kuppeln und weitere Gewölbe. Anhand dieser Erfahrungen und dem Wissen der Vorkriegszeit erfolgten internationale Verbreitung und Weiterentwicklung der Schalenbauweise.
Der Aufschwung in der Nachkriegszeit zeigte in der Suche nach neuen Formen und Entwicklungen folgende Errungenschaften auf diesem Gebiet:
- Entwicklung doppelt gekrümmter Flächen
- Einführung neuer Formen
- Tendenz zu größeren Spannweiten, was daraus resultierte, dass man versuchte, große Flächen ohne Träger zu überdachen
- Vorfertigung der Schalen als Tendenz zur Wirtschaftlichkeit.
Flächentragwerke gewannen nach 1945 im Bereich von Ingenieurkonstruktionen an Bedeutung und kamen neuen Gestaltungsideen in der Architektur entgegen. Neben der Funktion als Gebäudehülle kommen Schalenkonstruktionen auch in Bereichen wie Fahrzeug- und Flugzeugbau (siehe: Monocoque), dem Innenausbau und dem Möbelbau vor. Sie stellen ein wichtiges Gestaltungselement der Gegenwartskunst dar.
Wegen der komplizierten Anforderungen an Statik und Material wurden Schalen in den Jahrzehnten vor der Jahrtausendwende nur noch selten realisiert. Erst durch die Einführung neuer Materialien wurden dem Schalenbau in jüngerer Zeit wieder neue Impulse gegeben.
Tragverhalten
Die Biegesteifigkeit dünnwandiger oder schlanker Strukturen ist wesentlich geringer als ihre Dehnsteifigkeit in tangentialer Richtung. Um das Tragverhalten solcher Strukturen optimal auszunutzen, gilt es also, eine Biegebeanspruchung möglichst zu vermeiden.
Gekrümmte Stäbe können bei günstig gewählter Form und Lagerung Lasten biegefrei abtragen:
- Unter einer konstanten Streckenlast muss die Bogenlinie beispielsweise eine Parabel sein, damit ein biegefreier Zustand eintreten kann.
- Unter Eigengewicht stellt sich die Kettenlinie (Kosinus hyperbolicus) als biegefreie Form ein.
Bei Schalen ergeben sich wegen der Flächenwirkung wesentlich günstigere Verhältnisse. Eine Schale kann im Gegensatz zum Bogen Stützfläche für mehr als eine Flächenlast sein. Umgekehrt kann eine gegebene Last durch unterschiedliche Schalenformen membrangerecht abgetragen werden. Eine optimale Schalenform gibt es daher nicht.
Membranspannungszustand
Unter bestimmten Voraussetzungen werden bei einer Schale die Belastungen vorrangig durch über die Wandstärke konstant verteilte und zur Mittelfläche parallele Spannungen zu den Stützen hin abgeleitet. In solchen Fällen wird von einem Dehnspannungs- oder Membranspannungszustand gesprochen. Er liegt auch im Scheibenspannungszustand ebener Flächentragwerke (Scheiben) vor. Im Membranspannungszustand wird das Tragverhalten des Materials optimal ausgenutzt.
Voraussetzungen für den Membranspannungszustand sind:
- Die Mittelfläche ist stetig gekrümmt und weist keine sprunghaften Krümmungsänderungen auf.
- Die Schalendicke ändert sich nicht sprunghaft.
- Die Lasten senkrecht zur Schalenmittelfläche werden flächenverteilt aufgebracht (Punktlasten werden vermieden).
- Die Lasten ändern sich nicht sprunghaft.
- Durch die Lagerung werden keine Querkräfte oder Momente eingeleitet, d. h. die Lagerung erfolgt in tangentialer Richtung der Schale.
- Die Querverformung und Verdrehung der Schale wird durch die Lager nicht behindert.
- Die Temperaturverteilung über die Dicke der Schale ist konstant.
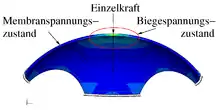
Wird eine dieser Voraussetzungen verletzt, so kommt es zum ungünstigeren Biegespannungszustand.
Das Bild rechts zeigt eine Kuppelschale, die in ihrer Mitte mit einer Einzelkraft belastet wird. In der Umgebung der Krafteinleitung, welche die dritte Bedingung für den Membranspannungszustand verletzt, liegt ein Biegespannungszustand vor (grün). Fernab der Krafteinleitung liegt jedoch der Membranspannungszustand vor (blau), denn die Kuppel ist stetig gekrümmt, und die Lagerung erfolgt tangential ohne Behinderung einer Drehung der Schale.
Biegespannungszustand
Durch Störung des Membranspannungszustandes bilden sich in der Umgebung der Störstelle über die Dicke variierende Biegespannungen und Schubspannungen senkrecht zur Mittelfläche aus. Einen solchen Zustand der Schale bezeichnet man als Biegespannungszustand. Nach dem Prinzip von St. Venant klingen die Störungen mit dem Abstand zur Störstelle rasch ab.
Der Biegespannungszustand kann mit dem Plattenspannungszustand ebener Flächentragwerke verglichen werden. Im Gegensatz zu diesen entkoppeln sich jedoch infolge der Krümmung die Membran- und Biegespannungszustände beim Schalenproblem nicht.
Allgemeine Eigenschaften
Empfindlichkeit gegen Imperfektionen
Weil die Biegespannungen gegenüber den Membranspannungen sehr groß werden können, ist das Tragverhalten einer Schale empfindlich gegenüber Unregelmäßigkeiten in der Form oder der Belastung. Eine ungenügende Berücksichtigung oder in Folge von Imperfektionen auftretende Verletzungen der Voraussetzungen für den Membranspannungszustand haben unter Umständen gravierende Auswirkungen. Aus diesem Grund ist es wichtig in den Berechnungsverfahren alle Eigenschaften einer Schale möglichst genau abzubilden.
Schalenformen
Neben den weitgehend beliebig und unregelmäßig geformten Blechen im Fahrzeugbau treten insbesondere in der Bautechnik oft einfache Schalenformen auf. Diese entstehen
Unterscheidung nach der Erzeugung
- durch Verschiebung einer ebenen Kurve oder Geraden (siehe: Regelfläche) entlang einer anderen Kurve, zum Beispiel bei Gewölben, Tonnendächern, Röhren
- durch Drehung/Rotation einer ebenen Kurve, der Meridiankurve, um eine in ihrer Ebene liegende Rotationsachse.
Zu diesen Rotationsschalen gehören (s. auch die Abbildungen unten):
- Häufig werden unterschiedliche Rotationsschalen miteinander kombiniert, z. B. eine (endlich lange) Zylinderschale mit Halbkugelschalen an den Enden. Die Rotationsschalen können in vielen Fällen mit der Membrantheorie (s. u.) berechnet werden.
Unterscheidung nach der Gaußschen Krümmung
Hinsichtlich der Gaußschen Krümmung werden unterschieden:
- : positiv gekrümmte Schalen (z. B. Kugeln, Kuppeln)
- : abwickelbare Schalen (z. B. Tonnen, Kegel)
- : negativ gekrümmte Schalen (z. B. Hyperboloide, Sattelflächen)
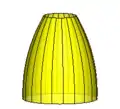Buckelfläche mit
Abwickelbare Fläche mit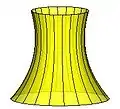
Hyperboloid mit
Berechnung
Annahmen
Bei der Berechnung von Schalen kann oftmals folgendes vorausgesetzt werden:
- Die Schalendicke ist klein im Vergleich zu den übrigen Abmessungen.
- Die Verformungen sind klein im Vergleich zur Schalendicke.
- Punkte, die auf einer Normalen zur Mittelebene liegen, befinden sich auch nach einer Verformung wieder auf einer solchen Geraden, ähnlich wie bei den Bernoullischen Annahmen der Balkentheorie.
- Senkrecht zur Mittelebene wirkende Normal- und Schubspannungen sind vernachlässigbar klein.
- Der Werkstoff ist homogen und isotrop und folgt dem Hookeschen Gesetz.
Abweichungen von diesen Voraussetzungen bedingen in der Regel weit höheren Berechnungsaufwand.
Spezielle Problemstellungen, insbesondere im Zusammenhang mit der modernen Werkstoffforschung (Verbundwerkstoffe u. ä.), machen die Herleitung höherer Schalentheorien erforderlich, z. B. von Multi-Direktor- und Mehrschichten-Schalentheorien, bei denen meist alle o. g. vereinfachenden Annahmen nicht gelten können.
Membrantheorie
Die Membrantheorie geht von weiteren Vereinfachungen aus. Sie ergibt keine genauen Lösungen, reicht jedoch für viele Anwendungsfälle aus.
- Durch die geringe Wanddicke sind die Biegesteifigkeiten und die inneren Biegemomente klein. Durchbiegungen werden daher vernachlässigt. Die maximalen Biegemomente treten in den Randbereichen auf.
- Es treten nur Normal- und Schubspannungen auf, die innerhalb der Ebene liegen und über die Wandstärke (Membrandicke) konstant sind.
- Der Einfluss der Formänderung auf den Kräfteverlauf wird vernachlässigt. Das Tragwerk wird also praktisch im unverformten Zustand untersucht (Theorie I. Ordnung).
- Der Rand einer Membranschale ist frei oder tangential abgestützt.
- Die Kräfte an den Schalenrändern sind tangential zur Mittelebene gerichtet.
Ein Spannungszustand in Schalen, der den Bedingungen der Membrantheorie entspricht, wird als Membranspannungszustand bezeichnet. Er ist Grundlage der Kesselformel.
Biegetheorie
Wenn die Voraussetzungen der Membrantheorie nicht oder nicht annähernd gegeben sind, muss die Biegetheorie angewendet werden, d. h. die Biegesteifigkeit der Schale muss berücksichtigt werden, bei dicken Schalen u. U. auch die endliche Schubsteifigkeit.
Manchmal genügt es, nach der Anwendung der Membrantheorie die Einwirkungen der Biegetheorie lokal nachträglich zu berücksichtigen. Das gilt vor allem, wenn der Rand der Schale gelenkig oder eingespannt abgestützt ist und damit die Bedingungen der Membrantheorie nicht erfüllt sind. Andere Beispiele sind die Übergänge zwischen unterschiedlichen Rotationsschalen.
Materialien
Schalen sind oftmals komplizierter zu entwerfen und zu fertigen als andere Tragwerke, benötigen aber in der Regel einen geringeren Materialeinsatz.
Schalen können monolithisch hergestellt werden, wobei in der Regel Stahlbeton eingesetzt wird. Alternativ werden sie aus vorgefertigten Einzelteilen zusammengesetzt, etwa aus gewölbten Stahlblechen, oder als Gittertragwerk (Gitterschale).
Das Skelett der Gittertragwerke besteht häufig aus Stahl, Holz (siehe Zollingerbauweise) oder Verbundwerkstoffen und kann mit textilen Baustoffen, Glas oder anderen Materialien ausgefacht bzw. überspannt werden. Die Ausfachungen können dabei statische Funktionen übernehmen oder lediglich als Verkleidungselement bzw. Raumabschluss dienen.
Seit Frei Otto sind weitspannende leichte Flächentragwerke ein Begriff. Forschungsgruppen befassten sich hierbei nicht nur mit der Weiterentwicklung der Konstruktionsarten, sondern auch mit der Kombination verschiedener Baumaterialien. Beim „Membran-Beton-Verbundbau“ (Textilbeton) werden die speziellen Materialeigenschaften von Beton und Membran miteinander kombiniert.
Früher wurden Gewölbe aus Materialien wie Stein, Lehm und Mauerwerk hergestellt.
Beton
Besonders für freie nicht-geometrische Formen ist Beton ideal. Er ist leicht zu verarbeiten und ermöglicht eine bestmögliche Umsetzung des Entwurfes. Beton ist wirtschaftlich und in jedem Klima einsetzbar. Aber er hat auch Nachteile: besonders bei Schalenkonstruktion können durch eine zu schnelle Austrocknung Probleme auftreten. Durch eine Polystyrolhülle oder andere Maßnahmen kann die Verdunstung des Wassers verzögert werden, so dass der Beton langsamer aushärtet und eine höhere Festigkeit erzielt wird.
Stahlbeton
Stahl und Beton wirken in Fällen, wo in Betonteilen Biege- und Zugspannungen auftreten, als Verbundbaustoff Stahlbeton zusammen. Weil beide Baustoffe eine annähernd gleiche Wärmeausdehnung aufweisen, bleibt diese Verbundwirkung auch bei Temperaturschwankungen erhalten. Bis zu einer gewissen Grenze entspricht das Tragverhalten von Stahlbetonbauteilen denjenigen aus Stahl oder unbewehrtem Beton. Der Verbund zwischen Stahl und Beton stellt dabei sicher, dass die erforderliche Rissbildung auf ein unschädliches Maß beschränkt wird. Stahlbeton eignet sich besonders zur Herstellung monolithischer Flächentragwerke, die sich durch hohe Steifigkeit und geringe Verformungen auszeichnen.
Glas
Da Glas als Bauwerkstoff ein sehr sprödes Materialverhalten aufweist, erfordert es gerade für konstruktiv tragende Scheiben die Reduktion von Biege- und Zugspannungen.
Glas wird hauptsächlich bei Gitterschalenkonstruktionen als Eindeckung für große verkrümmte Dachkonstruktionen verwendet.
Kunststoff
Im Bausektor werden in Zukunft sicherlich vermehrt Kunststoffe zur Ausführung tragender Bauteile herangezogen. Besonders Thermoplaste (Acrylate) und Duroplaste haben große Bedeutung erlangt. Diese Kunststoffe besitzen eine Reihe vorteilhafter Eigenschaften: wetterfest, meist sehr widerstandsfähig gegen Chemikalien, hohe Festigkeiten, geringes Gewicht und zum Teil lichtdurchlässig.
Holz
Große Tonnen, Kuppeln sowie andere freie Schalenformen mit Breiten um 20 Meter und Längen um 50 Meter können künftig aus Holzwerkstoffen hergestellt werden. Dieser Aspekt bedeutet, dass in der zeitgenössischen Architektur freie Flächentragwerke durch einfache Systeme verwirklicht werden können. Am besten eignet sich für dieses Vorhaben der Holzwerkstoffverbund. Ausgangsmaterial hierfür ist ein Werkstoffverbund aus Dreischicht-, Sperrholz- oder Sandwichplatten. Diese Hölzer werden mit zweikomponentigen Klebstoff auf textile Trägergewebe aus Polyester und Glasfasern geklebt. Dadurch kann das Tragwerk flächenmäßig hergestellt, die einzelnen Bahnen zur Baustelle transportiert und dort montiert werden.
Bauweisen
Die Schalenbauweise ist eine Form moderner Raumtragwerke.
Bis heute ist es zur Gestaltung der Schalen gängig, mathematisch definierte geometrische Formen zu wählen. Die Zeit der einfach gekrümmten Formen ist jedoch vorbei; nun stehen dem Architekten doppelt gekrümmte Flächen zur Verfügung, von Kuppeln bis hin zu hyperbolischen Paraboloiden. Fast all diese Formen sind quadratisch, was auch bedeutet, dass damit zusammenhängende Probleme wie Spannungen, Formänderungen und Weiteres besser erforscht wurden als früher.
Ein Prinzip könnte heißen: „Wählt man die richtige Form (beim architektonischen Entwurf), so ist die halbe Arbeit bereits getan. Dies heißt, der Geometrie ihren richtigen Platz zuweisen.“
Auch der Herstellungsprozess kann die Form von Schalen beeinflussen. Häufig werden sie vorgefertigt, Holzschalen schon seit Jahrzehnten. Dabei werden die einzelnen Elemente in einer Größe hergestellt, die leicht zu transportieren und zu heben ist. Mit der Vorfertigung wird die Einsparung an Materialaufwand als vorrangig bei der Entwicklung angestrebt. Die Relation zwischen Form und Tragfähigkeit ist im Bauwesen kaum irgendwo enger als bei Schalenkonstruktionen. Dank der Weiterentwicklungen erfordern Schalenkonstruktionen, verglichen mit anderen Baukonstruktionen, minimalen Materialaufwand.
Vorgefertigte Schalen findet man seit Ende der 1940er Jahre besonders im Industriebau. Da man Vorfertigung auch für allgemeine Bauten ermöglichen wollte, wurden sie in folgende Arten eingeteilt:
- „Vorgefertigte Schalenkonstruktionen mit besonderer Aufgabenstellung für Konstruktion, Funktion, Gestaltung und Repräsentation. In diesem Falle ist oft eine Anwendung der als Einzelfertigung auf der Baustelle oder auch im Werk hergestellten Fertigteile gerechtfertigt“
- „Vorgefertigte Schalenkonstruktionen, die bei Industriebauten in großer Häufigkeit verwendbar sind. Dazu gehören neben Dächern von Hallen- und Flachbauten, bei denen große Stützenabstände erwünscht sind, auch Dachkonstruktionen …“
Eine weitere Einteilung könnte erfolgen nach Werks- oder Baustellenfertigung sowie nach industrieller oder Einzelfertigung.
Auch für die Arbeitsmittel wurde zu Gunsten des Schalenbaus ein großer Schritt erzielt: war es noch vor Jahrzehnte ein großer Aufwand, geometrisch meist komplizierte Formen mit aufwendigen Holzschalungen zu verkleiden, so sind heute versetzbare, wiederverwendbare und kostengünstige Gerüste aus Metall verfügbar. So können statisch-konstruktive Formen monolithisch hergestellt werden.
Gitterschalen
Neben geschlossenen Schalen gibt es die Gitterschalen, biegesteife offene Flächentragwerke. Sie sind besonders geeignet für Eindeckungen wie große, gekrümmte Glasdächer. Sie sind alle Schalen dünnwandig und gekrümmt. Ihr Eigengewicht sowie Lasten, die von außen einwirken, werden größtenteils durch eine Normalkraftbeanspruchung in der Schalenmittelebene abgetragen (Membranspannungszustand). Zug- und Biegebeanspruchungen können durch das Heranziehen von Glasflächen als Aussteifung abgefangen werden.
Gitterschalen kann man auch als eine Schale mit vielen großen Öffnungen beschreiben. Allerdings darf das Tragverhalten dadurch nicht beeinträchtigt werden. Stellt man beispielsweise die Gitterschale aus einzelnen Stäben her, so müssen die Stabverbindungen in den Knotenpunkten und die Maschenart die Tragwirkung sicherstellen.
Bei sehr weit gespannten Gitterschalen können Stabilitätsprobleme wie das Beulen auftreten. Solche Schalen müssen mit aufwändigen Zusatzmaßnahmen wie Bögen, Rahmen, Seilüberspannungen o. ä. versehen werden. Rahmenartige Knotenpunkte müssen ausgeführt werden, wenn keine Diagonalen erwünscht sind.
Ein prominentes Beispiel für Gitterschalen ist die Multihalle in Mannheim.
Siehe auch
Literatur
- Ernest L. Axelrad: Schalentheorie. (= Leitfäden der Angewandten Mathematik und Mechanik; 58) Teubner Verl., Stuttgart 1983, ISBN 3-519-02360-1.
- Wilhelm Flügge: Statik und Dynamik der Schalen. 3. Aufl. Springer Verl., Berlin 1962 (Reprint: 1981), ISBN 3-540-02815-3.
- Johannes Altenbach, Wolfgang Kissing, Holm Altenbach: Dünnwandige Stab- und Stabschalentragwerke: Modellierung und Berechnung im konstruktiven Leichtbau. (= Grundlagen und Fortschritte der Ingenieurwissenschaften) Vieweg Verl., Braunschweig 1994, ISBN 3-528-06486-2.
Nachweise
- Roland May: Von Biebrich in die ganze Welt. Zur Verbreitung des Zeiss-Dywidag-Schalenbaus bis zum Ende des Zweiten Weltkriegs, in: Beton- und Stahlbetonbau, 111. Jg. (2016), H. 6, S. 385–396.
- Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Berlin: Ernst & Sohn 2018, S. 732–743, ISBN 978-3-433-03229-9.