Schalentheorie

Die Schalentheorie befasst sich mit den Eigenschaften und der Modellierung von Schalen. Schalen sind biegesteife Flächentragwerke, bei denen zwei Abmessungen gegenüber der dritten groß sind und die – in Abgrenzung zu den ebenen Flächentragwerken Scheibe und Platte – bereits unbelastet in allen drei Raumrichtungen gekrümmt sein können. Die Bilder rechts zeigen zwei typische Beispiele schalenartiger Strukturen: die hohlen Halme von Süßgräsern wie hier beim Bambus und eine Karosserie. Biegeschlaffe dünnwandige Strukturen wie Flug- oder Ballonhäute werden dagegen als Membranen bezeichnet.

Bambusstämme

Karosserie als Monocoque

Der Ursprung der Schalentheorie liegt im 19. Jahrhundert, also in einer Zeit, als es die modernen Berechnungsmöglichkeiten noch nicht gab. Heute werden Schalenmodelle vor allem für die Finite-Elemente-Methode (FEM) entworfen. Wegen der geringen Biegesteifigkeit der Schalen im Vergleich zu ihrer Dehnsteifigkeit in Dickenrichtung sind die Gleichungssysteme der FEM ohne Schalenmodelle schlecht konditioniert und können ausgedehnte, dünnwandige Strukturen nur mit Hilfe von Schalenmodellen berechnet werden. Die Effizienz der Schalenmodelle ist im Wesentlichen eine Folge der Einführung von speziellen kinematischen Annahmen für die Querschnittsverformung der Struktur, die es gestatten, das dreidimensionale Kontinuum auf ein zweidimensionales Modell zu reduzieren.

Schalen nutzen die Tragfähigkeit ihres Materials durch das Abtragen von Lasten über Membrankräfte, die über die Dicke der Schale konstant sind, optimal aus. So kommt es zur hohen Steifigkeit der Schalen bei gleichzeitig geringem Gewicht und Materialeinsatz, die ihnen in der Natur und Technik eine bedeutende Rolle verschaffen. In der Natur kommen Schalen in den Vogeleierschalen, den Außenskeletten von Gliederfüßern (Insekten, Spinnen, Krebse), Knochen (Schädel, Schulterblatt) oder Halmen von Süßgräsern vor. In der Technik finden sich Schalen in Silos oder Kuppelbauten, Karosserien oder Trägern.

Historischer Abriss

Das optimale Verhalten von gekrümmten Tragwerken war schon den Baumeistern der Antike bekannt. Zahlreich erhaltene Viadukte und Straßenbrücken, vor allem aber das Pantheon in Rom, sind auch heute noch eindrucksvolle Zeugen von dieser Kenntnis. Versuche, das Tragverhalten von Schalen rechnerisch zu erfassen, wurden bereits vor mehr als fünfhundert Jahren gemacht. Dabei waren vor allem Überlegungen über den Kraftfluss und die daraus folgende, optimale Form der Wölbung von Mauerwerkskuppeln von Bedeutung. Einen ausführlichen Überblick über die historische Entwicklung der Berechnung von Bögen und Schalen, die vor allem im Zusammenhang mit Mauerwerkskuppeln stattfand, gaben Edoardo Benvenuto[1] und Karl-Eugen Kurrer[2].

Im Laufe des neunzehnten Jahrhunderts verlagerten sich die Überlegungen über das Deformations- und Tragverhalten von Schalen von anschaulichen, mechanischen Betrachtungen und Methoden der graphischen Statik hin zu eher mathematisch orientierten, analytischen Theorien. Bei den ersten Versuchen, eine Biegetheorie der Schalen aufzustellen, ging es nicht um das Tragverhalten von Kuppeln, sondern um die Ermittlung der Eigenfrequenzen von Glocken, um deren optimale Form für den gewünschten Klang analytisch bestimmen zu können. August E. H. Love (1888)[3] schrieb in seinem berühmten Aufsatz: “This paper is really an attempt to construct a theory of the vibrations of bells” (zu deutsch: Dieser Aufsatz ist tatsächlich ein Versuch eine Theorie der Schwingungen von Glocken aufzubauen)[4]. Verfeinerungen der Theorie kamen von Mindlin und Reissner.[5] Diese Theorien waren noch auf linear-elastische Medien und kleine Verformungen eingeschränkt.

Die Gebrüder Eugène und François Cosserat(1909)[6] führten das gerichtete Kontinuum von Duhem (1893)[7] in die Schalentheorie ein, was von Naghdi (1972)[8] zum Vorläufer der sogenannten geometrisch exakten Schalentheorie ausgebaut wurde[9].

Mit dem Siegeszug der FEM seit den 1970er Jahren wird in Schalenmodellen die Reduktion des dreidimensionalen Kontinuums auf ein zweidimensionales (mittels Integration über die Dicke der Schale) numerisch ausgeführt, was die Berücksichtigung großer Deformationen und beliebiger Materialmodelle gestattet.[4][9]

Bezeichnungen an der Schale

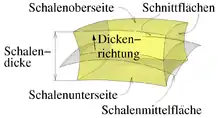
In der Abbildung rechts ist ein Ausschnitt einer Schale dargestellt (gelb). Der Schalenkörper wird durch die Schalenoberseite (obere Laibungsfläche) nach oben und mit der Schalenunterseite (untere Laibungsfläche) nach unten begrenzt. Mittig zwischen der Schalenober- und -unterseite befindet sich die Schalenmittelfläche (grau). Der Abstand zwischen der Schalenober- und -unterseite ist die Schalendicke, die also durch die Mittelfläche halbiert wird. Die Dickenrichtung verläuft von der Schalenunter- zur Schalenoberseite und die tangentiale Richtung parallel zur Schalenmittelfläche. Mit Schnittflächen können Partien der Schale herausgeschnitten werden.

Numerik

Typische Schalenstruktur

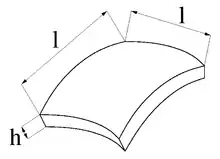
Bei der numerischen Lösung von Anfangsrandwertaufgaben mit der FEM tritt folgendes Problem auf: Die Dehnsteifigkeit in Dickenrichtung einer linear elastischen, isotropen, viereckigen Schale mit Kantenlänge l und Dicke h wie im Bild ist proportional zu E l²/h, wenn E der Elastizitätsmodul des Schalenmaterials ist. Die Dehnsteifigkeit in Dickenrichtung ist bei abnehmender Schalendicke h wesentlich größer als die Biegesteifigkeit, die proportional ist zu E l h³/l³. Das Verhältnis zwischen Dehnsteifigkeit in Dickenrichtung und Biegesteifigkeit ist damit proportional zu (l/h)⁴, wobei Werte von l/h>1000 keine Seltenheit sind. Bei der Addition dieser Steifigkeiten im Rechner wird die Biegesteifigkeit an das Ende des begrenzt langen Computerwortes verschoben, was eine schlechte Konditionierung des resultierenden Gleichungssystems und mit h → 0 sogar eine singuläre Steifigkeitsmatrix bedingen kann. Durch Unterdrückung von Änderungen der Schalendicke während der Deformation wird die Dehnsteifigkeit in tangentialer Richtung der Schale, die proportional zu E h l/l ist, zur größten Schalensteifigkeit, weswegen das Verhältnis zwischen größter und kleinster Steifigkeit auf (l/h)² abnimmt.

Durch eine Unterdrückung von Verzerrungen in Dickenrichtung kann außerdem die maximal zulässige Zeitschrittweite bei expliziten dynamischen Analysen nach der Courant-Friedrichs-Lewy-Bedingung von h/c auf l/c – nicht selten um einen Faktor zehn und mehr – vergrößert werden, wobei c die Wellenausbreitungsgeschwindigkeit in der physikalischen Struktur ist.

Schalenmodelle

Schalenkinematik mit Schalenmittelfläche

{\vec {X}}^{m}

(blau) und einer Abweichung in Dickenrichtung (rot)

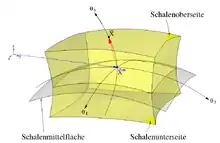
Die Effizienz der Schalentheorie ist im Wesentlichen eine Folge der Einführung von speziellen kinematischen Annahmen für die Querschnittsverformung der Struktur. Allen Schalenmodellen gemeinsam ist, dass der Ortsvektor eines Punktes innerhalb der Schale aufgeteilt wird in eine Komponente, die auf die Schalenmittelfläche weist, in der Abbildung rechts blau, und einer Abweichung in Dickenrichtung (rot), die durch Direktoren beschrieben wird. Anders als die Normalenvektoren von Flächen sind die Direktoren im Allgemeinen nicht senkrecht zur Schalenmittelfläche.

Einteilung

Die Schalenmodelle lassen sich in folgende Gruppen einteilen:

klassische Schalentheorie oder Schalentheorie basierend auf dem Degenerationskonzept,
schubstarre Kirchhoff’sche und schubweiche Schalen,
Schalenmodelle mit oder ohne Dickenänderung bei der Verformung,
Schalentheorien höherer Ordnung oder Multi-Direktor Theorie sowie
Schalentheorien eines konventionellen oder eines Cosserat-Kontinuums.

Klassische Schalentheorie und Degenerationskonzept

Die beiden Hauptströmungen der Schalentheorie sind die klassische Schalentheorie und das Degenerationskonzept. Die den beiden Konzepten zu Grunde liegenden kinematischen Annahmen sind im Wesentlichen die gleichen. In der klassischen Schalentheorie wird die Integration der Spannungen über die Dicke zu Spannungsresultierenden vorab analytisch erledigt, was bei linear elastischem Verhalten, kleinen Verformungen und in ebenen (Scheiben und Platten) und rotationssymmetrischen (Röhren, Kugeln und Hyperboloide) Strukturen mit vertretbarem Aufwand gelingt. Die Spannungsresultierenden müssen in Folge der Impuls- und Drehimpulsbilanz partiellen Differenzialgleichungen genügen. Im Degenerationskonzept wird die Integration über die Schalendicke im konkreten Berechnungsfall numerisch durchgeführt. N. Büchter[10] bewies 1992, dass Schalenelemente der beiden Herangehensweisen zu gleichen Ergebnissen führen.

Schubstarre und schubweiche Schalen

Bei der schubstarren Kirchhoff’schen Schale bleiben die Direktoren, die im Ausgangszustand senkrecht zu der Schalenmittelfläche sind, auch während der Verformung senkrecht zur Schalenmittelfläche, was der bernoullischen Annahme bei den Balken entspricht. Diese Annahme ist bei sehr dünnen Tragwerken gerechtfertigt, liefert aber auch dort für die höheren Eigenfrequenzen zunehmend falsche Ergebnisse. Die Erweiterung der Theorie zu schubweichen Schalen, wo die Direktoren ihre Winkel zur Schalenmittelfläche ändern können, ist in guter Übereinstimmung mit experimentellen Fakten.[11]

Theorie höherer Ordnung und Multi-Direktor-Theorie

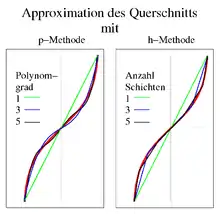
Approximation der Querschnittsverwölbung mit p- und h-Methode

Im Aufbau der Spannungsresultierenden unterscheiden sich die Schalentheorien höherer Ordnung und die Multi-Direktor-Theorie. Bei der Theorie höherer Ordnung stellt der deformierte Schalenquerschnitt eine knickfreie gewölbte Fläche dar. Diese Theorien können aus einer Taylor-Reihenentwicklung der Verformung in Dickenrichtung abgeleitet werden und führen auf die hierarchischen Modelle, die ein besseres Lösungsverhalten durch höherwertige Ansatzfunktionen zu erreichen versuchen. In der FEM wird dies p-Methode zur Verbesserung der Approximation genannt, siehe Abbildung rechts linker Bildteil. Die klassische Schalentheorien von Kirchhoff-Love[3] und Reissner[5] stellen danach eine Theorie nullter bzw. erster Ordnung dar und entstehen durch Vernachlässigung von Termen höherer Ordnung in Dickenrichtung.

Die Multi-Direktor-Theorien andererseits nehmen stückweise lineare Verläufe der materiellen Linien in Dickenrichtung an. Diese kinematische Annahme wurde vielfach auf geschichtete Laminatschalen angewendet.[12] Indem die Stücke immer kürzer werden, kann prinzipiell jeder Funktionsverlauf über die Dicke approximiert werden, was mit der h-Methode in der FEM korrespondiert, siehe Abbildung rechts rechter Bildteil.

Dicke und dünne Schalen

Schalenmodelle, die eine Dickenänderung während der Verformung erlauben, werden „dicke Schalen“ genannt, im Gegensatz zu den „dünnen Schalen“, die eine unveränderliche Dicke aufweisen. Bei dicken Schalen muss sorgfältig zwischen der Orientierungsänderung und der Längenänderung von materiellen Linienelementen in Dickenrichtung der Struktur unterschieden werden. Die Unterdrückung einer Längenänderung des Direktors während der Deformation, wie es in dünnen Schalen geschieht, basiert auf der Annahme, dass die Normalspannungen in Dickenrichtung der Schale klein sind und ist demnach nur zulässig, wenn weder konzentrierte Beanspruchungen – im Extremfall Einzelkräfte – noch stark unterschiedliche entgegengesetzte Flächenkräfte an der Schalenober- und -unterseite eingeleitet werden.

Wenn die Dicke der Schale unveränderlich ist, dann verschwinden die Normaldehnungen in Dickenrichtung, was aber auf Grund der Querkontraktion im Widerspruch zur Annahme der nur kleinen Normalspannungen in Dickenrichtung ist. Das Verschwinden der Normalspannungen in Dickenrichtung, die Degenerationsbedingung, muss daher auf Materialgleichungsebene durch sogenannte Kondensation berücksichtigt werden.[13] Kondensierte Materialgleichungen sind für viele Stoffmodelle nicht vorhanden oder umständlich in der Formulierung. Bei der numerischen Berechnung, z. B. in der FEM, kann die Kondensation durch numerische Verfahren für beliebige Materialmodelle erreicht werden.[14] Alternativ kann auch ein Ansatz höherer Ordnung genommen werden, der eine Dickendehnung darstellen kann.

Konventionelles oder Cosserat-Kontinuum

Die Schalentheorie höherer Ordnung liefert ähnliche Gleichungen wie die auf Cosserat-Kontinua[6] basierende Schalentheorie. In einem Cosserat-Kontinuum hat jeder Raumpunkt nicht nur drei Freiheitsgrade für die Bewegung in die drei Raumrichtungen, sondern noch zusätzliche Verdrehfreiheitsgrade, mit denen in der direkten Methode die Direktoren der Schale parametrisiert werden. Das Hauptproblem der direkten Vorgehensweise besteht darin, die Schnittgrößen, Verzerrungen und Krümmungen mit Spannungen und Verzerrungen des dreidimensionalen Körpers in Zusammenhang zu bringen. Die direkte Methode entspricht im Wesentlichen dem, was heute in der Literatur als geometrisch exakte Schalentheorie bezeichnet wird. Die Bezeichnung „exakt“ unterstreicht hier aber nur, dass die Theorie nicht aus einer approximativen Taylor-Reihenentwicklung hervorgeht, wie es die Multi-Direktor-Theorie tut.

Reduktion der Dimension

Wie eingangs erwähnt, werden seit den 1970er Jahren die Schalentheorien vor allem für die FEM formuliert. Eine weit verbreitete Grundgleichung der FEM ist das in der Kontinuumsmechanik formulierte Prinzip von d’Alembert in der Lagrange’schen Fassung, in dem die virtuelle Deformationsarbeit

\delta W_{\text{int}}:=\int _{V}\delta w_{\text{int}}\;\mathrm {d} V

zu berechnen ist. Darin ist V das Gebiet der Schale, $\delta w_{\text{int}}$ die virtuelle Spannungsarbeit und $\mathrm {d} V$ die Volumenform der Schale. Die Effizienz der Schalenmodelle ist im Wesentlichen eine Folge der Einführung einer speziellen Schalenkinematik, die es durch Einführung von Spannungsresultierenden, als integrale Größen über die Dicke, gestattet das Volumenintegral im dreidimensionalen Kontinuum auf ein Flächenintegral eines zweidimensionalen Modells zu reduzieren.

Schalenkinematik

Ausgangskonfiguration der Schale

Das Gebiet der Schale wird mit konvektiven Koordinaten ${\vec {\Theta }}=(\Theta _{1},\Theta _{2},\Theta _{3})\in \mathbb {R} ^{3}$ abgedeckt, wobei die ersten beiden Koordinaten die Schalenmittelfläche parametrisieren und $\Theta _{3}$ die Dickenrichtung, siehe Abbildung rechts. Der Ortsvektor eines Punktes innerhalb der Schale (schwarz im Bild) wird aufgeteilt in eine Komponente ${\vec {X}}^{m}$ , die auf die Schalenmittelfläche weist (blau im Bild), und einer Abweichung in Dickenrichtung (rot im Bild), die durch Direktoren ${\vec {D}}_{n},n={1,2},\ldots ,N$ beschrieben wird:

{\vec {X}}={\vec {\chi }}_{0}({\vec {\Theta }})={\vec {X}}^{m}(\Theta _{1},\Theta _{2})+\sum _{n=1}^{N}f_{n}(\Theta _{3}){\vec {D}}_{n}(\Theta _{1},\Theta _{2})

.

Wie üblich werden Größen in der undeformierten Ausgangslage zu einer Zeit $t_{0}$ mit Großbuchstaben bezeichnet. Der Vektor

{\vec {X}}=\sum _{i=1}^{3}X_{i}{\vec {e}}_{i}

beinhaltet die materiellen Koordinaten $X_{i}({\vec {\Theta }})$ des Partikels bezüglich der Standardbasis ${\vec {e}}_{1,2,3}$ . Anders als die Normalenvektoren von Flächen sind die Direktoren im Allgemeinen nicht senkrecht zur Schalenmittelfläche. Die Multi-Direktor Theorie basiert auf stückweise linearen Funktionen $f_{n}$ . Hier sollen stattdessen Potenzen von $\Theta _{3}$ eingesetzt werden:[8]

{\vec {X}}={\vec {\chi }}_{0}({\vec {\Theta }})={\vec {X}}^{m}(\Theta _{1},\Theta _{2})+\sum _{n=1}^{N}\Theta _{3}^{n}{\vec {D}}_{n}(\Theta _{1},\Theta _{2})=\sum _{n=0}^{N}\Theta _{3}^{n}{\vec {D}}_{n}(\Theta _{1},\Theta _{2})

,

wenn ${\vec {D}}_{0}:={\vec {X}}^{m}$ gesetzt wird. In dem $N\rightarrow \infty$ geht, wird eine reale Schalengeometrie mit der Funktion ${\vec {\chi }}_{0}$ immer besser wiedergegeben werden können.

Die Koordinatenfläche mit $\Theta _{3}=H(\Theta _{1},\Theta _{2})/2$ definieren dann die Schalenoberseite, $\Theta _{3}=-H(\Theta _{1},\Theta _{2})/2$ die Unterseite und $\Theta _{3}=0$ gibt die Schalenmittelfläche an. Platten- und Scheibenstrukturen sind als derjenige Spezialfall enthalten, wo die Schalenmittelfläche ${\vec {X}}^{m}$ eben und die Direktoren ${\vec {D}}_{1,2,\ldots }$ senkrecht zur Schalenmittelfläche sind.

Die Bewegungsfunktion

{\vec {x}}={\vec {\chi }}({\vec {\Theta }},t)=\sum _{n=0}^{N}\Theta _{3}^{n}{\vec {d}}_{n}(\Theta _{1},\Theta _{2},t)

ist von der Zeit $t$ abhängig und liefert die Momentankonfiguration, deren Variablen mit Kleinbuchstaben bezeichnet werden. Die Komponenten des Vektors ${\vec {x}}$ heißen „räumliche Koordinaten.“

Parametrisierung der Direktoren

Bei nicht schubstarren Schalen können die Direktoren mit der Zeit gegenüber der Schalenmittelfläche ihre Orientierung ändern. Die Orientierung der Direktoren wird mit Rotationsparametern beschrieben, welche – wie die Direktoren – nur von den Koordinaten $\Theta _{1},\Theta _{2}$ abhängen. Als Rotationsparameter werden benutzt:

Euler-Winkel, die Drehwinkel um bestimmte Achsen angeben,
Quaternionen,
Rotationsvektoren, die durch ihre Richtung die Drehachse bestimmen und der Drehwinkel eine Funktion ihres Betrages ist, siehe Orthogonaler Tensor, und
Differenzen der Verschiebungen an der Schalenober- und -unterseite.

Die Euler-Winkel haben den Nachteil, dass verschiedene Euler-Winkel dieselbe Drehung beschreiben können. In diesen Fällen tritt bei der Ableitung des Direktors nach den Euler-Winkeln eine Singularität auf. Dies ist bei der Benutzung von Quaternionen nirgends der Fall. Die Singularität entfällt auch bei Rotationsvektoren, wenn ihre Beträge der Drehwinkel in Radiant ist.[10] Die Parametrisierung von Schalenelementen basierend auf den Differenzen der Verschiebungen an der Schalenober- und -unterseite weist Eigenschaften von Kontinuumselementen und Schalenelementen auf ("Kontinuumsschalen"). Dort werden die Vorteile eines Kontinuumsansatzes mit denen der Schalentheorie verknüpft.[4]

Basisvektoren im Schalenraum

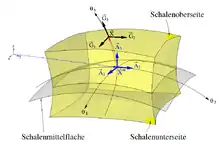
Ausgangskonfiguration der Schale

Die Ableitung des Ortes nach den konvektiven Koordinaten $\Theta _{1,2,3}$ liefert die kovarianten Basisvektoren (im Bild rechts schwarz)

{\begin{array}{rcl}{\vec {G}}_{\alpha }({\vec {\Theta }})&=&\displaystyle {\frac {\partial {\vec {\chi }}_{0}}{\partial \Theta _{\alpha }}}=\sum _{n=0}^{N}\Theta _{3}^{n}{\vec {D}}_{n,\alpha }(\Theta _{1},\Theta _{2}),\;\alpha \in \lbrace {1,2}\rbrace \\{\vec {G}}_{3}({\vec {\Theta }})&=&\displaystyle {\frac {\partial {\vec {\chi }}_{0}}{\partial \Theta _{3}}}=\sum _{n=1}^{N}n\Theta _{3}^{n-1}{\vec {D}}_{n}(\Theta _{1},\Theta _{2})\end{array}}

.

Hier und im Folgenden laufen griechische Indizes von eins bis zwei und ein Komma im Index $(\cdot )_{,k}$ bedeutet eine Ableitung nach der Koordinate $\Theta _{k}$ . Die zur kovarianten Basis duale Basis stellen die Gradienten

{\vec {G}}^{\alpha }=\sum _{i=1}^{3}{\frac {\partial \Theta _{\alpha }}{\partial X_{i}}}{\vec {e}}_{i},\quad {\vec {G}}^{3}=\sum _{i=1}^{3}{\frac {\partial \Theta _{3}}{\partial X_{i}}}{\vec {e}}_{i}

,

dar, die die kontravarianten Basisvektoren bilden (im Bild nicht dargestellt). Die ko- und kontravarianten Basisvektoren der Mittelfläche bei $\Theta _{3}=0$ werden mit einem großen A bezeichnet

{\begin{array}{rclclllcl}{\vec {A}}_{\alpha }(\Theta _{1},\Theta _{2})&:=&{\vec {G}}_{\alpha }(\Theta _{1},\Theta _{2},0)&=&{\vec {D}}_{{0,}\alpha }(\Theta _{1},\Theta _{2}),&{\vec {A}}^{\alpha }(\Theta _{1},\Theta _{2})&:=&{\vec {G}}^{\alpha }(\Theta _{1},\Theta _{2},0)\\{\vec {A}}_{3}(\Theta _{1},\Theta _{2})&:=&{\vec {G}}_{3}(\Theta _{1},\Theta _{2},0)&=&{\vec {D}}_{1}(\Theta _{1},\Theta _{2}),&{\vec {A}}^{3}(\Theta _{1},\Theta _{2})&:=&{\vec {G}}^{3}(\Theta _{1},\Theta _{2},0)\end{array}}

und hängen per Definition nicht von der Dickenkoordinate $\Theta _{3}$ ab (im Bild blau). Die ko- und kontravarianten Basisvektoren in der Momentankonfiguration werden analog mit den räumlichen Koordinaten definiert:

{\begin{array}{rcllrcl}{\vec {g}}_{\alpha }({\vec {\Theta }},t)&=&\displaystyle {\frac {\partial {\vec {\chi }}({\vec {\Theta }},t)}{\partial \Theta _{\alpha }}}=\sum _{n=0}^{N}\Theta _{3}^{n}{\vec {d}}_{n,\alpha }(\Theta _{1},\Theta _{2}),&{\vec {g}}^{\alpha }&=&\displaystyle \sum _{i=1}^{3}{\frac {\partial \Theta _{\alpha }}{\partial x_{i}}}{\vec {e}}_{i}\\{\vec {g}}_{3}({\vec {\Theta }})&=&\displaystyle {\frac {\partial {\vec {\chi }}({\vec {\Theta }},t)}{\partial \Theta _{3}}}=\sum _{n=1}^{N}n\Theta _{3}^{n-1}{\vec {d}}_{n}(\Theta _{1},\Theta _{2}),&{\vec {g}}^{3}&=&\displaystyle {\frac {\partial \Theta _{3}}{\partial x_{i}}}{\vec {e}}_{i}\end{array}}

.

Schalenshifter

Der Tensor, der die Basisvektoren der Schalenmittelfläche ${\vec {A}}_{1,2,3}$ in den Schalenraum transformiert, wird Schalenshifter oder Shifttensor genannt:

\mathbf {Z

.

Mit ihm kann der (kovariante) Green-Lagrange’sche Verzerrungstensor

\mathbf {E} =\sum _{i,j=1}^{3}E_{ij}{\vec {G}}^{i}\otimes {\vec {G}}^{j}

im Schalenraum auf die Schalenmittelfläche transformiert werden:

\mathbf {E} ^{m}:=\mathbf {Z} ^{\mathrm {T} }\cdot \mathbf {E} \cdot \mathbf {Z} =\sum _{i,j=1}^{3}E_{ij}{\vec {A}}^{i}\otimes {\vec {A}}^{j}

.

Der in einem materiellen Punkt vorliegende Spannungstensor vom zweiten Piola-Kirchhoff Typ

{\tilde {\mathbf {T} }}=\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {G}}_{i}\otimes {\vec {G}}_{j}

ist kontravariant und wird mittels

\mathbf {Z} ^{-1}\cdot {\tilde {\mathbf {T} }}\cdot \mathbf {Z} ^{\mathrm {T} -1}=\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {A}}_{i}\otimes {\vec {A}}_{j}=:{\tilde {\mathbf {T} }}^{m}

auf die Schalenmittelfläche transformiert. Das Frobenius-Skalarprodukt „:“ der Tensoren bleibt von der Transformation unberührt:

${\tilde {\mathbf {T} }}:\mathbf {E} ={\tilde {\mathbf {T} }}^{m}:\mathbf {E} ^{m}$ .

Schnittgrößen

Die Komponenten des Green-Lagrange’schen Verzerrungstensors

${\begin{array}{rclrcl}E_{\alpha \beta }=E_{\beta \alpha }&=&\displaystyle {\frac {1}{2}}({\vec {g}}_{\alpha }\cdot {\vec {g}}_{\beta }-{\vec {G}}_{\alpha }\cdot {\vec {G}}_{\beta })&=&\displaystyle {\frac {1}{2}}\sum _{k=0}^{N}\sum _{l=0}^{N}\Theta _{3}^{k+l}({\vec {d}}_{k,\alpha }\cdot {\vec {d}}_{l,\beta }-{\vec {D}}_{k,\alpha }\cdot {\vec {D}}_{l,\beta })\\E_{\alpha 3}=E_{3\alpha }&=&\displaystyle {\frac {1}{2}}({\vec {g}}_{\alpha }\cdot {\vec {g}}_{3}-{\vec {G}}_{\alpha }\cdot {\vec {G}}_{3})&=&\displaystyle {\frac {1}{2}}\sum _{k=0}^{N}\sum _{l=1}^{N}\Theta _{3}^{k+l-1}l({\vec {d}}_{k,\alpha }\cdot {\vec {d}}_{l}-{\vec {D}}_{k,\alpha }\cdot {\vec {D}}_{l})\\E_{33}&=&\displaystyle {\frac {1}{2}}({\vec {g}}_{3}\cdot {\vec {g}}_{3}-{\vec {G}}_{3}\cdot {\vec {G}}_{3})&=&\displaystyle {\frac {1}{2}}\sum _{k=1}^{N}\sum _{l=1}^{N}\Theta _{3}^{k+l-2}kl({\vec {d}}_{k}\cdot {\vec {d}}_{l}-{\vec {D}}_{k}\cdot {\vec {D}}_{l})\end{array}}$

werden in Komponenten $E_{nij}^{m}$ aufgeteilt, die nur von den Koordinaten der Schalenmittelfläche abhängen:

E_{ij}({\vec {\Theta }})=\sum _{n=0}^{2N}\Theta _{3}^{n}E_{nij}^{m}(\Theta _{1},\Theta _{2})

.

Multiplikation mit den Dyaden ${\vec {A}}^{i}\otimes {\vec {A}}^{j}$ und Summation über alle Indizes liefert so die Zerlegung:

\mathbf {E} ^{m}=\sum _{n=0}^{2N}\Theta _{3}^{n}\mathbf {E} _{n}^{m}(\Theta _{1},\Theta _{2})

.

Die virtuelle Spannungsarbeit ist das Frobenius-Skalarprodukt der Spannungen mit virtuellen Verzerrungen, die wie die Komponenten des Verzerrungstensors in die Dickenkoordinate entwickelt werden:

\delta w_{\text{int}}={\tilde {\mathbf {T} }}:\delta \mathbf {E} ={\tilde {\mathbf {T} }}^{m}:\delta \mathbf {E} ^{m}=\sum _{n=0}^{2N}\Theta _{3}^{n}{\tilde {\mathbf {T} }}^{m}:\delta \mathbf {E} _{n}^{m}

.

Für das Volumenintegral wird das Volumenelement des Schalenraumes multiplikativ in das Oberflächenelement der Mittelfläche und einen Rest zerlegt:

\mathrm {d} V=\det({\vec {G}}_{1},{\vec {G}}_{2},{\vec {G}}_{3})\,\mathrm {d} \Theta _{1}\mathrm {d} \Theta _{2}\mathrm {d} \Theta _{3}=\underbrace {\frac {\mathrm {det} ({\vec {G}}_{1},{\vec {G}}_{2},{\vec {G}}_{3})}{|{\vec {A}}_{1}\times {\vec {A}}_{2}|}} _{:=Z}\;\mathrm {d} \Theta _{3}\,\underbrace {|{\vec {A}}_{1}\times {\vec {A}}_{2}|\mathrm {d} \Theta _{1}\mathrm {d} \Theta _{2}} _{:=\mathrm {d} A^{m}}=Z\,\mathrm {d} \Theta _{3}\mathrm {d} A^{m}

.

Integration der virtuellen Spannungsarbeit über das Schalenvolumen liefert mit den bereitgestellten Definitionen

{\begin{array}{rcl}\delta W_{\text{int}}&=&\displaystyle \int _{V}\delta w_{\text{int}}\,\mathrm {d} V=\int _{A^{m}}\int _{-H/2}^{H/2}\delta w_{\text{int}}Z\,\mathrm {d} \Theta _{3}\,\mathrm {d} A^{m}\\&=&\displaystyle \int _{A^{m}}\sum _{n=0}^{2N}\underbrace {\int _{-H/2}^{H/2}\Theta _{3}^{n}{\tilde {\mathbf {T} }}^{m}Z\,\mathrm {d} \Theta _{3}} _{:={\hat {\mathbf {N} }}_{n}}:\delta \mathbf {E} _{n}^{m}\mathrm {d} A^{m}=\int _{A^{m}}\sum _{n=0}^{2N}{\hat {\mathbf {N} }}_{n}:\delta \mathbf {E} _{n}^{m}\mathrm {d} A^{m},\end{array}}

also ein Flächenintegral über die Arbeit des effektiven Schnittgrößentensors ${\hat {\mathbf {N} }}_{n}$ an virtuellen Verzerrungen $\delta \mathbf {E} _{n}^{m}$ in der Schalenmittelfläche. Die Komponenten

N_{nij}=\int _{-H/2}^{H/2}\Theta _{3}^{n}{\tilde {T}}^{ij}Z\,\mathrm {d} \Theta _{3}

werden Ersatzschnittgrößen oder auch symmetrische Schnittgrößen genannt, denn sie entstehen nicht durch Integration von Schnittkräften über eine Schnittfläche sind aber symmetrisch ( $N_{nij}=N_{nji}$ ).

Bei linearer Elastizität

{\tilde {\mathbf {T} }}^{m}={\stackrel {4}{\mathbf {C} }}{}^{m}:\mathbf {E} ^{m}

mit konstantem Elastizitätstensor vierter Stufe ${\stackrel {4}{\mathbf {C} }}{}^{m}$ kann die Entwicklung des Verzerrungstensors in die Dickenkoordinate vorteilhaft eingesetzt werden:

\mathbf {N} _{n}=\int _{-H/2}^{H/2}\Theta _{3}^{n}{\tilde {\mathbf {T} }}^{m}Z\,\mathrm {d} \Theta _{3}=\sum _{l=0}^{2N}\int _{-H/2}^{H/2}\Theta _{3}^{n+l}{\stackrel {4}{\mathbf {C} }}{}^{m}Z\,\mathrm {d} \Theta _{3}:\mathbf {E} _{l}^{m}.=:\sum _{l=0}^{2N}{\stackrel {4}{\mathbf {D} }}_{l}:\mathbf {E} _{l}^{m}.

So kann für die symmetrische Schnittgröße eine Materialgleichung angegeben werden.

Der Schnittgrößentensor, der durch eine Integration von Schnittspannungen über Schnittflächen der Schale entsteht, ist im Allgemeinen unsymmetrisch. Das liegt daran, dass die Schnittspannungen über den im Allgemeinen unsymmetrischen ersten Piola-Kirchoff-Spannungstensor mit den Schnittflächennormalen zusammenhängen. Nur in ebenen Flächentragwerken (Scheiben und Platten) ist der effektive Schnittgrößentensor gleich dem Schnittgrößentensor.

Siehe auch

Klassische Laminattheorie

Literatur

Évariste Sanchez-Palencia, Olivier Millet, Fabien Bechet: Singular Problems in Shell Theory: Computing and Asymptotics. Springer, 2010, ISBN 978-3-642-13814-0.
H. Altenbach, J. Altenbach, R. Rikards: Einführung in die Mechanik der Laminat- und Sandwichtragwerke. Deutscher Verlag für Grundstoffindustrie, 1996.
P. M. Naghdi: The theory of shells and plates. In: S. Flügge (Hrsg.): Handbuch der Physik, Band 6a 2. Festkörpermechanik. Springer-Verlag, 1972, ISBN 3-540-05535-5, ISBN 0-387-05535-5.

Weblinks

J. Matheas: Arbeitsschwerpunkte Schalentheorie

Einzelnachweise

E. Benvenuto: An Introduction to the History of Structural Mechanics, Part II: Vaulted Structures and Elastic Systems. Springer, 1991.
K.-E. Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, 2018.
A.E.H. Love: On the small vibrations and deformations of thin elastic shells. In: Philosophical Transactions of the Royal Society, 179, 1888, S. 491 ff.
J. Irslinger: Mechanische Grundlagen und Numerik dreidimensionaler Schalenelemente. 2013, ISBN 978-3-00-044707-5 (Bericht Nr. 61, Institut für Baustatik, Universität Stuttgart).
E. Reissner: The effect of transverse shear deformation on the bending of elastic plates. In: Journal of applied mechanics, Trans. ASME, Vol. 67, Nr. 2, 1945, S. 69–77
E. Cosserat, F. Cosserat: Théorie des corps déformables. Hermann & Cie, Paris, 1909
P. Duhem: Le potentiel thermodynamique et la pression hydrostatique. In: Annales scientifiques de l’École Normale Supérieure. 10 (1893), S. 183–230.
P. M. Naghdi (1972)
M. Bischoff: Theorie und Numerik einer dreidimensionalen Schalenformulierung. 1999 (ibb.uni-stuttgart.de [PDF] Bericht Nr. 30, Institut für Baustatik, Universität Stuttgart).
N. Büchter: Zusammenführung von Degenerationskonzept und Schalentheorie bei endlichen Rotationen. 1992 (ibb.uni-stuttgart.de [PDF] Bericht Nr. 14 des Instituts für Baustatik der Universität Stuttgart).
Altenbach [1996, S. 290ff]
F. Gruttmann: Theorie und Numerik dünnwandiger Faserverbundstrukturen. Habilitationsschrift am Fachbereich Bauingenieur- und Vermessungswesen der Universität Hannover, Bericht-Nr. F 96/1, Universität Hannover, 1996 (uni-hannover.de).
R. D. Mindlin: Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic Elastic Plates. In: Journal of Applied Mechanics. Nr. 18, 1951, ISSN 0021-8936, S. 31–38.
C. Huettel, A. Matzenmiller: Consistent discretization of thickness strains in thin shells including 3D-material models. In: Communications in applied numerical methods. Band 15, 1999, S. 283–293.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] E. Benvenuto: An Introduction to the History of Structural Mechanics, Part II: Vaulted Structures and Elastic Systems. Springer, 1991.

[2] K.-E. Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, 2018.

[love88-3] A.E.H. Love: On the small vibrations and deformations of thin elastic shells. In: Philosophical Transactions of the Royal Society, 179, 1888, S. 491 ff.

[irslinger-4] J. Irslinger: Mechanische Grundlagen und Numerik dreidimensionaler Schalenelemente. 2013, ISBN 978-3-00-044707-5 (Bericht Nr. 61, Institut für Baustatik, Universität Stuttgart).

[reissner45-5] E. Reissner: The effect of transverse shear deformation on the bending of elastic plates. In: Journal of applied mechanics, Trans. ASME, Vol. 67, Nr. 2, 1945, S. 69–77

[cosserat09-6] E. Cosserat, F. Cosserat: Théorie des corps déformables. Hermann & Cie, Paris, 1909

[7] P. Duhem: Le potentiel thermodynamique et la pression hydrostatique. In: Annales scientifiques de l’École Normale Supérieure. 10 (1893), S. 183–230.

[naghdi72-8] P. M. Naghdi (1972)

[bischoff-9] M. Bischoff: Theorie und Numerik einer dreidimensionalen Schalenformulierung. 1999 (ibb.uni-stuttgart.de [PDF] Bericht Nr. 30, Institut für Baustatik, Universität Stuttgart).

[buechter92-10] N. Büchter: Zusammenführung von Degenerationskonzept und Schalentheorie bei endlichen Rotationen. 1992 (ibb.uni-stuttgart.de [PDF] Bericht Nr. 14 des Instituts für Baustatik der Universität Stuttgart).

[11] Altenbach [1996, S. 290ff]

[12] F. Gruttmann: Theorie und Numerik dünnwandiger Faserverbundstrukturen. Habilitationsschrift am Fachbereich Bauingenieur- und Vermessungswesen der Universität Hannover, Bericht-Nr. F 96/1, Universität Hannover, 1996 (uni-hannover.de).

[13] R. D. Mindlin: Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic Elastic Plates. In: Journal of Applied Mechanics. Nr. 18, 1951, ISSN 0021-8936, S. 31–38.

[14] C. Huettel, A. Matzenmiller: Consistent discretization of thickness strains in thin shells including 3D-material models. In: Communications in applied numerical methods. Band 15, 1999, S. 283–293.