Lager (Statik)

Lager im Sinne der Statik bzw. Baustatik sind abstrahierte Verbindungen zwischen einem Starrkörper (Tragwerk) und seiner Umgebung, mit deren Hilfe Bewegungen des Körpers eingeschränkt und Kräfte aufgenommen werden. Die vom Lager ausgehenden Kraftgrößen, die den Kräften und Momenten des Körpers entgegenwirken, werden als Lagerreaktionen bezeichnet, siehe auch Actio und Reactio.

Balken auf zwei Stützlagern (Auflager); links: Festlager; rechts: Loslager
Die Abstützung auf den Spitzen der Dreiecksymbole drückt aus, dass das Lager Drehmomenten nicht entgegen wirkt, Drehungen also zulässt. Die kleinen Kreise auf den Spitzen deuten an, dass das Auflager als Drehlager anzusehen ist.

Lager, die zwei Körper bzw. Tragwerke miteinander verbinden, werden als Gelenke bezeichnet.[1] Nur wenn ein Tragwerk statisch bestimmt ist, lassen sich Lagerkräfte bzw. Reaktionen aufgrund der verschiedenen Lasten berechnen. Ein Tragwerk ist dann statisch bestimmt, wenn es durch äußere Kräfte nicht einfach verschoben werden kann (statisch unterbestimmt), oder äußere Kräfte zu Verformungen führen (statisch überbestimmt). Beispielsweise knickt ein beidseitig eingespannter Stab aus, wenn sich das Material erwärmt und damit ausdehnt, da keine der beidseitigen Einspannungen nachgibt.

Lager unterscheiden sich durch ihre Fähigkeit verschiedene Grundkräfte aufnehmen zu können. Im 2D Raum, sind das bis zu drei, denn jede Last, die auf ein Lager wirkt, kann in horizontale Kräfte, vertikale Kräfte und Momente (Drehmomente) zerlegt werden, siehe auch Kräfteparallelogramm.

Im Dreidimensionalen sind es bis zu sechs Grundkräfte, nämlich je 3 translatorische Kräfte in die jeweiligen Achsenrichtungen, sowie je ein Moment um die entsprechende Achse. Somit kann ein Lager im Dreidimesionalen eine Wertigkeit zwischen 1 und 6 aufweisen.

Ein Lager, dass alle auftretenden Kräfte aufnehmen kann, wird als Einspannung bezeichnet.

Lagerarten

2D-Lagerarten von Bernoulli-Stäben

	Randbedingung in x	Randbedingung in z	Randbedingung um y	Wertigkeit
vers. Einspannung	N=0	V=0	φ=0	1 (M)
vert. Wegfeder	N=0	V=k·w	M=0	1 (V)
hor. vers. Auflager	N=0	w=0	M=0	1 (V)
hor. vers. Einspannung	N=0	w=0	φ=0	2 (V,M)
Drehfeder	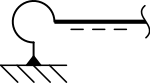N=0	V=0	M=c·φ	1 (M)
vert. vers. Auflager	u=0	V=0	M=0	1 (N)
ver. vers. Einspannung	u=0	V=0	φ=0	2 (N,M)
Festlager	u=0	w=0	M=0	2 (N,V)
Einspannung	u=0	w=0	φ=0	3 (N,V,M)
gedrehtes Auflager	N+V=0, 　 u=w		M=0	1 (V/N)

Alle Auflager in der Tabelle sind im Stabkoordinatensystem definiert und können in einem globalen Koordinatensystem beliebig orientiert sein. Das im Stabkoordinatensystem gedrehte Auflager soll exemplarisch verdeutlichen, dass alle Lager in beliebiger Orientierung verwendet werden können. Eine Verschieblichkeit wird durch eine doppelten Linie, eine Verdrehbarkeit durch den Kreis an der Spitze eines Dreiecks symbolisiert. In der Realität sind alle Auflager nachgiebig und entsprechen einer gefederten Lagerung. Im Maschinenbau sind Stäbe meistens statisch bestimmt gelagert, sodass Auflagersetzungen und Auflagersteifigkeiten keine Auswirkungen haben und somit eine Betrachtung als starres Auflager zulässig ist.

Im Bauwesen sind Tragwerke jedoch meist statisch überbestimmt. In der statischen Berechnung von Teilsystemen werden Nachgiebigkeiten von Auflagern dennoch oft vereinfacht als starr angenommen. In der statischen Berechnung treten somit häufig Einspannungen, feste und horizontal verschiebliche Auflager auf. Da Geschossdecken üblicherweise zweiachsig gespannt werden, ist oft eine 3-Dimensionale Berechnung notwendig. Im 3-Dimensionalen übernimmt man die 2D-Lagersymbole oft analog, da dies oft nicht eindeutig ist, beschreibt man hier oftmals die Rand- und Übergangsbedingungen.

3D-Lagerarten

Da es im Dreidimensionalen sechs Grundkräfte gibt, treten hier mehr unterschiedliche Lagerarten entsprechend den möglichen Kombinationen an Grundkräften auf – angefangen vom hochwertigsten Lager, der Einspannung mit Wertigkeit 6, bis zum einfachen Auflager, das nur die senkrechte (Gewichts-)Kraft ("in den Boden") aufnehmen kann.

Ein Rohr, das beispielsweise als Lager für einen dadurch geführten Rundstab dient, lässt einerseits eine Verschiebung in Achse des Rohres zu, andererseits eine Verdrehung um die Rohrachse. Da damit also die anderen vier der sechs Grundkräfte vom Rohr aufgenommen werden können (Bewegung entlang zwei Achsen sowie Verdrehung um zwei Achsen), handelt es sich hier um ein vierwertiges Lager.

Berechnung der Lagerreaktionen

Bei einem statisch bestimmten Tragwerk lassen sich Lagerkräfte mithilfe der Gleichgewichtsbedingungen berechnen:

\Sigma F_{ix}=0,\quad \Sigma F_{iy}=0,\quad \Sigma M_{i}^{(P)}=0

Die Gleichungen drücken aus, dass die Summen aller horizontalen Kräfte, vertikalen Kräfte und Momente (inklusive Lagerkräfte) bei einem ruhenden Körper jeweils gleich Null sein müssen. Die einzelnen Lagerkräfte errechnen sich durch die Auflösung dieses Gleichungssystems.[2]

Beispiel

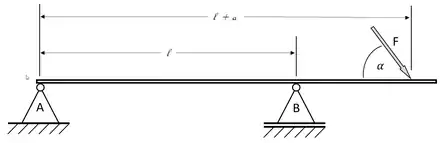
Der abgebildete gewichtslose Balken wird von einem Festlager A auf der linken und einem Loslager B auf der rechten Seite getragen. Auf der der rechten Seite greift eine Kraft F an. Da es sich bei A um ein Festlager handelt, kann Auflager A sowohl horizontale wie auch vertikale Kräfte aufnehmen. Lager B, das Loslager, kann hingegen nur vertikale Kräfte aufnehmen.

Zunächst wird das Tragwerk "freigeschnitten". Dafür ersetzt man die Lager durch die Kräfte, die sie aufnehmen können, und teilt jede angreifende Kraft in ihre jeweiligen Komponenten in Bezug auf das Lager. In diesem Fall ergibt sich also $F_{y}=F\,sin\,\alpha$ und $F_{x}=F\,cos\,\alpha$ .

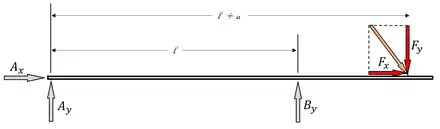
Damit können nun die folgenden Gleichgewichtsbedingungen aufgestellt werden.

Die Summe aller horizontalen Kräfte ist:

\Sigma F_{ix}=0=A_{x}+F_{x}

$A_{x}$ ist also $-F_{x}$ . Da hier $A_{x}$ einen negativen Wert ergibt, ist die im Bild angenommene Kraftrichtung grafisch falsch gewählt, die tatsächliche Auflagerkraft zeigt in die entgegengesetzte Richtung.

Die Summe aller vertikalen Kräfte ist:

\Sigma F_{iy}=0=A_{y}+B_{y}-F_{y}

Diese Gleichung mit zwei Unbekannten lässt sich erst durch zusätzliches Aufstellen des Momentengleichgewichts lösen. Dies kann prinzipiell an jedem Punkt erfolgen. In der folgenden Gleichung wird das Momentengleichgewicht um Auflager B gewählt:

\Sigma M_{i}^{B}=0=A_{y}\cdot l+F_{y}\cdot a

Man beachte, dass beide Kräfte positiv aufgeführt sind, obwohl sie in unterschiedliche Richtungen zeigen, da beide Kräfte im Balken ein Drehmoment im Uhrzeigersinn auslösen (bei Aufstellung des Momentengleichgewichts um Auflager A würden die Kräfte entgegengesetzt gerichtete Drehmomente bewirken). Durch Auflösen der Gleichung erhält man für $A_{y}$ :

A_{y}=-F_{y}\cdot {\frac {a}{l}}

Auch hier ist die Kraft $A_{y}$ im Lager A negativ. Das Lager hält also den Balken mit der Auflagerkraft nach unten. Ist das Lager nicht dazu fähig, würde der Balken nach oben kippen und sich um Punkt B drehen. Bei der Untersuchung muss darauf geachtet werden, dass das statische Modell die Wirklichkeit intuitiv abbildet, bzw. man sollte sich der Modellfehler bewusst sein.

Mit dem Ergebnis für $A_{y}$ lässt sich nun zum Schluss $B_{y}$ durch Einsetzen berechnen:

0=-F_{y}\cdot {\frac {a}{l}}+B_{y}-F_{y}

B_{y}=F_{y}\cdot {\frac {a}{l}}+F_{y}

B_{y}=F_{y}\ ({\frac {a}{l}}+1)

Feste und verschiebliche Einspannung

Eine (feste) Einspannung[3] ist ein Lager, das sowohl Verschiebungen in alle drei Richtungen als auch Verdrehungen um alle drei Achsen im Lagerpunkt unterbindet, wie es beispielsweise beim Köcherfundament der Fall ist.

Ein Loslager auf dem Mittelpfeiler einer Eisenbahnbrücke. Die Fahrbahn ruht verschieblich auf Stahlrollen.

Eine verschiebliche Einspannung ist eine Gleitführung, welches Verschiebungen (meist in eine oder zwei Richtungen), aber keine der drei Verdrehungen im Lagerpunkt zulässt.[3]

Festlager (Fixlager) und Loslager (verschiebliches Lager)

Siehe auch: Fest-Los-Lagerung (Maschinenbau)

Ein Festlager unterbindet alle Verschiebungen und ermöglicht eine oder mehrere Verdrehungen im Lagerpunkt.
Damit ein Körper sich nicht dreht oder kippt, muss er neben dem Festlager in der Ebene an mindestens einer weiteren Stelle, im Raum an mindestens zwei weiteren Stellen gelagert werden.[4]

Ein Loslager wird auch als verschiebliches Auflager oder Gleitlager bezeichnet. Es unterbindet eine oder zwei Verschiebungen (darunter gewöhnlich die Verschiebung durch die Gewichtskraft) und lässt die anderen Verschiebungen und eine oder mehrere Verdrehungen im Lagerpunkt zu.[4]

Die Begriffe Fest- und Loslager werden meist im Zusammenhang verwendet. Beispielsweise wird eine drehbar gelagerte Welle gewöhnlich mit einem unverschieblichen Kugel- oder Gleitlager als Festlager ausgeführt, um zu verhindern, dass die gesamte Welle sich verschiebt. Weitere Lager der Welle werden hingegen als Loslager ausgeführt, um axiale Zwangsspannungen aufgrund der Wärmedehnung der Welle bei Temperaturveränderungen zu vermeiden. Aus dem gleichen Grund werden Fest- und Loslager im Brückenbau angewendet.

Eine durch entsprechende Anordnung von Fest- und Loslagern statisch bestimmte Konstruktion lässt sich einfach berechnen, da keine Rücksicht auf zusätzliche Kräfte und Momente durch Zwangsspannungen in den Lagern genommen werden muss, wie sie bei der Belastung von statisch überbestimmten Tragwerken entstehen.

Fest- und Loslager mit Gelenk werden auch als unverschiebliche bzw. verschiebliche Gelenklager bezeichnet.[5]

Siehe auch

Lager (Maschinenelement) – Lagertypen des Maschinenbaus
Lager (Bauwesen) – Lagertypen im Bauwesen
Baugrund – Auflager eines Bauwerks
Lagerungskonzepte
Baustatik

Literatur

Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik 1. Springer, 2019, doi:10.1007/978-3-662-59157-4.

Einzelnachweise

Baustatik 1 – Gelenke, In: Ingenieurkurse.de; abgerufen im März 2020.
Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik 1. 2019, doi:10.1007/978-3-662-59157-4 (springer.com [abgerufen am 12. Oktober 2020]).
Sigurd Falk: Biegen, Knicken und Schwingen des mehrfeldrigen geraden Balkens. In: Abhandl. Braunschweig. Wiss. Ges. Band 7, 1955, S. 74–92 (archive.org [PDF]).
Bernd Markert: Mechanik 1, Stereostatik, Statik starrer Körper. Aachen 2014, S. 73–77.
Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik 1. 2019, doi:10.1007/978-3-662-59157-4 (springer.com [abgerufen am 12. Oktober 2020]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Baustatik 1 – Gelenke, In: Ingenieurkurse.de; abgerufen im März 2020.

[2] Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik 1. 2019, doi:10.1007/978-3-662-59157-4 (springer.com [abgerufen am 12. Oktober 2020]).

[falk1955biegen-3] Sigurd Falk: Biegen, Knicken und Schwingen des mehrfeldrigen geraden Balkens. In: Abhandl. Braunschweig. Wiss. Ges. Band 7, 1955, S. 74–92 (archive.org [PDF]).

[markert-4] Bernd Markert: Mechanik 1, Stereostatik, Statik starrer Körper. Aachen 2014, S. 73–77.

[5] Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik 1. 2019, doi:10.1007/978-3-662-59157-4 (springer.com [abgerufen am 12. Oktober 2020]).